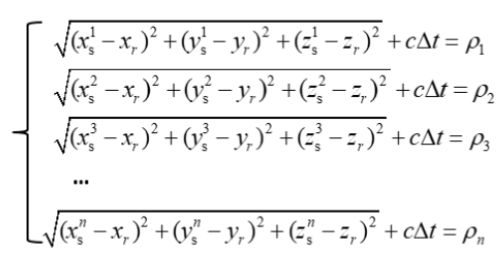GNSS（一）：定位和定向基本原理

一、基础概念

普通接收机通多伪距定位，定位精度在米级，而测量型接收机对载波相位的测量精度可以达到毫米级，通过其它手段消去GNSS卫星的轨道误差、钟差、大气传输误差之后，可以实现静态厘米级甚至毫米级的定位。本文档主要介绍高精度的定向和定位如何实现。

定向：设备上会有两个天线，通过对双天线组成的基线矢量的测量实现航向角和横滚角解算

RTK（(Real Time Kinematic）定位：在已知位置的参考点上设参考基站，与待定位的流动站构成基线矢量，利用基站差分数据和流动站GNSS观测数据进行基线解算，结合基站位置， 获得流动站位置。RTK定位其实是一个相对定位，通过在位置已知点上部署一个参考站，利用移动站与参考站误差源高度空间与时间相关性，做差分消去GNSS卫星的轨道误差、钟差以及大部分的电离层误差、对流层误差，进而实现厘米级的定位。

二、全球定位系统基础（Global Positioning system）

1.概览

目前GNSS卫星总计有120+颗卫星，其中北斗2和北斗3加起来移动44+颗。

工作频段1.1G-1.6GHz,北斗，GPS,伽利略和GLONASS对应工作频段不同。

如果想知道接收机的位置，至少需要同时跟踪三颗卫星才能定位，考虑到接收机时钟存在钟差，需要至少四颗及以上卫星才能进行定位。

因此卫星导航系统：
输入：

• 四颗或者以上卫星的位置
• 接收机到卫星的距离$\rho =r+c\ast dt$

输出：

• 接收机位置和钟差（receiver’s clock bias）
  注意：信号需要直线传播（多径，可能有几十米的误差）、卫星几何形状分布较好有利于解算。
  求解方程如下：
  

2.坐标系介绍

a. Earth Centered Inertial (ECI) Frame

• 原点为地球质心，x为春分点，z为地球转轴
• ECI is an inertial frame in which Newton’s laws of motion apply
• Earth rotates along the z axis of ECI
  
  satellite position $r_s(t)$ is in ECI, 为了考虑地球自转对卫星位置的影响，我们需要将卫星的位置从地心惯性坐标系（ECI）转换到地心地固坐标系（ECEF）,同时计算卫星位置要考虑萨格纳克效应，指的是由于地球自转而导致的光速在地球表面上不同位置的传播时间不同。这会对卫星的位置测量和导航产生影响。为了考虑萨格纳克效应，我们需要在计算卫星位置时考虑光速的变化。

综上所述，要计算考虑地球自转和萨格纳克效应的卫星位置rs(t)在ECI中，我们需要进行以下步骤：

• 根据卫星的测量数据或轨道模型，获取卫星的初始位置和速度。
• 考虑地球自转，将卫星的位置和速度从ECI转换到ECEF坐标系。
• 考虑萨格纳克效应，根据卫星位置和速度的变化，调整卫星的位置。
• 根据调整后的卫星位置，进行进一步的计算或导航应用。

b.Earth Centered Earth Fixed(ECEF) Frame

• 原点为地球中心，z为北方，x轴位于赤道平面上，并指向本初子午线。
• the axis rotate relative to the ECI frame with7.292115*10(-5)rad/s
• 考虑到地球的旋转，ECEF is a non-inertial frame

我们最后算出的GNSS位置都是在ECEF坐标系下的位置。
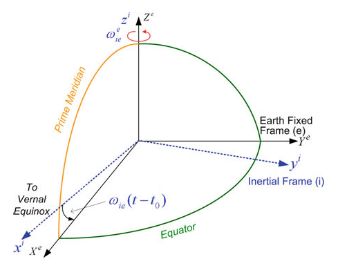
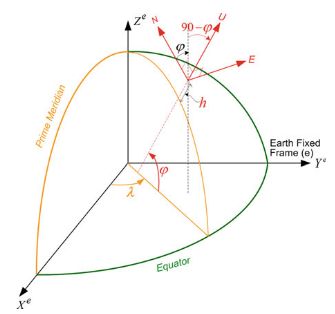
Transformation Between ECI and ECEF：如下图所示，差了个地球自转
)
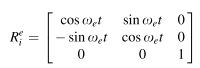$w_e$ denotes the magnitude of the Earth’s rotation rate.
)

c. NED OR ENU

局部切平面坐标系相对于地球有一个固定的原点，通常是地表上的一个点。它的坐标轴与地形方向对齐。

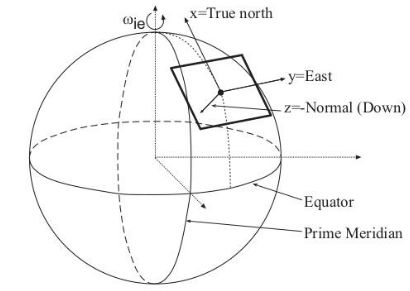
ECEF坐标系（Earth-Centered, Earth-Fixed）是一种以地球中心为原点，以地球自转轴为Z轴的坐标系。NED坐标系（North-East-Down）是一种以参考点为原点，以地球表面的局部切平面为XY平面的坐标系。要将一个点的ECEF坐标转换为NED坐标，可以按照以下步骤进行操作：

• 确定参考点的ECEF坐标和地理坐标（纬度、经度、海拔）。
• 将参考点的地理坐标转换为ECEF坐标。
• 将待转换点的ECEF坐标减去参考点的ECEF坐标，得到相对于参考点的ECEF坐标差值。
• 将ECEF坐标差值转换为地理坐标差值（纬度、经度、海拔差值）。
• 根据参考点的地理坐标，将地理坐标差值转换为NED坐标。
  
  转换的旋转矩阵为：
  
  

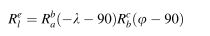
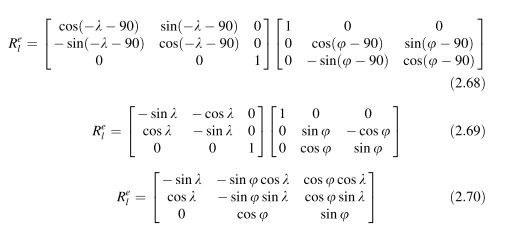
3.细节原理

每个卫星发送射频信号，包含pseudo-random noise (PRN) code以及导航消息。
PRN用于接收机找到传输时间(transit time)。

GPS观测包含伪距（pseudo-ranges measurements），载波相位（carrier phase measurements and）和多普勒（Doppler measurements）。下面分别进行介绍：

a. Pseudo-Ranges Measurements

伪距是卫星和接收机之间的距离，时间通过PRN code来计算。c为光速，则伪距：

来自第m个卫星的伪距测量可以写为：

GPS卫星在两个无线电频率上发送信号，分别称为L1和L2，它们的中心频率分别为1575.41和1227.60 MHz。每个频率都通过称为伪随机噪声（PRN）序列或码的测距码进行调制，用于精确的距离测量。粗略获取（C/A code）码与标准定位服务（SPS）相关联，专门用于民用。精确码（P-code）与精确定位服务（PPS）相关联。出于安全原因，P码进一步加密为P(Y)-code，仅供授权的军用用户使用。L1频率由C/A码和P码调制，而L2频率仅由P码调制。单个GPS接收器的精度约为5到30米。接收器必须确定卫星的位置，以便使用导航消息将距离测量转换为用户的位置和速度。导航消息与L1和L2载波以及PRN码叠加在一起。

b. Carrier Phase Measurements

计算RTK位置的时候才需要用到载波相位。GPS receiver可以准确测量一个周期的分数相位，但从卫星到接收器的完整周期数最初是未知的，整周模糊度（integer ambiguity）求解之后，就能通过载波$\lambda$和整周数N以及相位$\Phi$得到。这种方式计算的距离（range）比PRN code更加精确。
不同code以及载波相位精度如下：

• C/A-code: 1 / (1.0231e6hz) * (31e8m/s) = 293m, 293m * 1/100 = 2.93m
• P-code: 1 / (10.231e6hz) * (31e8m/s) = 29.3m, 29.3m * 1/100 = 0.293m
• Carrier-phase: 0.1-0.2cm
  
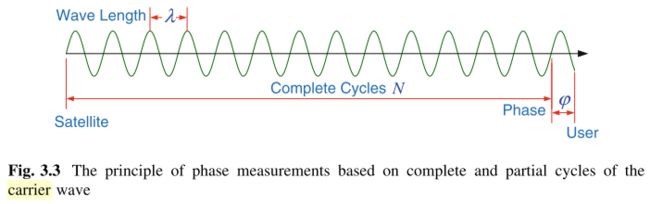
  载波计算的伪距为：
  
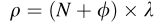
  考虑到钟差、大气延迟、测量误差等，可以写为：
  
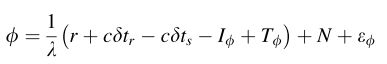
  其中N是整周模糊度（IA）。左右单位变成m,则可以转换成下式：
  
  由于电离层和对流层延迟与PRN相同，因此简化为：
  

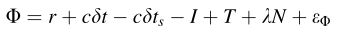
c. Doppler Measurements

多普勒效应是由发射器和接收器的相对运动引起的电磁信号频率偏移。基于这一现象，一些GPS接收器还通过测量接收信号的多普勒频率来计算用户的速度。The Doppler shift $f_d$,line-of-sight range rate $\dot{r}$,波长$\lambda$的关系为：

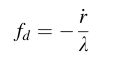
d. 误差来源（Error Sources）

• Satellite Clock Error: 随着时间的推移，卫星时钟会与GPS系统时间偏离。控制段根据监测站提供的观测卫星时钟数据，估计卫星时钟的校正参数，并将其上传到卫星上，卫星会在导航消息中广播这些参数，以使接收器能够根据测量的距离来纠正卫星时钟误差。

• Receiver Clock Error:接收器时钟的设计目的是为了价格实惠，因此它们的精度远低于卫星时钟，并且存在偏差。这种时钟偏差误差以相同的方式影响所有测量。因此，如果有四个伪距测量值可用，可以估计时钟偏差以及确定用户位置所需的三个分量。

• 电离层和对流层时延：电离层延迟通常影响更大
  

• 多径：多径效应是城市环境中的主要误差来源，GPS信号可以通过多条不同的路径到达接收器。这些路径包括直射路径和来自接收天线周围其他物体的反射信号。间接到达的信号会有延迟，并且信噪比较低。多径效应会在接收天线处与反射信号干扰导致原始信号失真。这可能导致超过10米的位置误差。对于载波相位测量而言，多径误差比伪距测量低两个数量级。码相位0.5-1m，载波相位0.5-1cm
  

• 星历误差：卫星轨道误差是卫星在空间中的实际位置与接收器使用星历数据计算的卫星位置之间的差异。根据卫星的先前运动和对地球引力的了解，控制段预测轨道误差，并将其上传到卫星上，作为星历数据广播给用户。由于星历模型是对测量轨道的曲线拟合，因此相对于实际轨道，它将包含时间变化的残余误差。通常，这个误差在2到5米之间。

• 接收机噪音：这是GPS接收器电子元件固有的随机测量噪声。它是由天线电路、电缆、热噪声、射频信号干扰、信号量化和采样的累积效应引起的。由于它是信噪比的函数，它随卫星的仰角而变化。它会导致对GPS信号的传输时间进行错误测量。与多径效应类似，对于载波相位测量而言，接收器噪声比伪距测量低两个数量级。码相位0.25-0.5m，载波相位0.1-0.2cm

三、定位定向原理

a.观测方程

定位和定向需要使用到的GNSS观测值为伪距和载波相位；观测方程为：

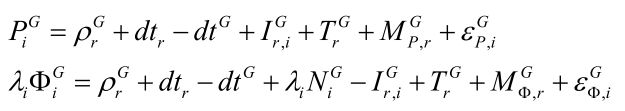
其中各个变量的物理含义为：
$P$表示伪距观测值
$\Phi$表示载波相位观测值；
$i$为频率标识
$\lambda$为相应频率信号的波长
$\rho$标识接收机至GNSS卫星的几何距离
$r$表示接收机
$d{t}_r$表示接收机钟差
$d{t}_G$表示GPS卫星端钟差
$I$表示信号传播过程中的电离层延迟误差
$T$表示信号传播过程中的对流层延迟误差
$N$表示模糊度
$M_{P,r}^G,M_{\Phi ,r}^G$分别表示码伪距和载波相位的多路径误差
${\epsilon }_{P,r}^G,{\epsilon }_{\Phi ,r}^G$分别表示码伪距和载波相位的观测噪声

b.观测误差来源及影响

从上式可以看到，GNSS观测误差主要来自于：
卫星时钟：

• 单点定位误差-模型校正后m级精度；
• 双差误差-0m

卫星星历：

• 单点定位误差-三维位置m级精度；
• 双差误差-cm级精度（10cm）,短基线同历元0

电离层延时：

• 单点定位误差-m级精度；
• 双差误差-cm级精度（20cm）,短基线同历元0

对流层延时：

• 单点定位误差-cm级精度(10cm-1m)；
• 双差误差-cm级精度（20cm）,短基线同历元0

多路径：

• 单点定位误差-码相位<2m,载波相位<1cm；

接收机噪声：

• 单点定位误差-码相位<0.5m,载波相位<0.3cm；

c.RTK差分(RTK double-Differencing)原理

RTK差分(RTK double-Differencing)原理如下图所示：Base和Vehicle都可以接收到Satelite J和Satelite K的信号，Satelite J的结果在Base和Vehicle做单差得到$P^J$, 同样Satelite K做单差得到$P^K$,$P^J$和$P^K$再做双差得到P;
第一步单差操作可以消除卫星误差和大气层误差；第二部双差可以消除接收机误差

伪距测量为：

带入观测方程

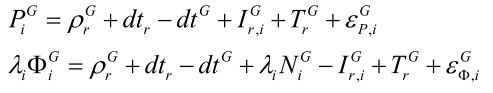
接收机位置$(x_r,y_r,z_r)$为待求参数，对观测方程进行线性化得到：

其中$(x_0,y_0,z_0)$为线性化点，RTK定位时，这也是基站位置，提前标定好的准确位置。

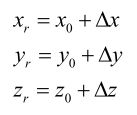
d.双差观测

影响卫星导航定位的各类误差中，大多具有较强的空间相关性，因而它们对定位结果的影响也 有一定的空间相关性。如果两个接收机距离比较近，即双天线为短基线，可以消除部分误差。

1）接收机做差

两个接收机$r_1$ 和 $r_2$同时观测卫星G1

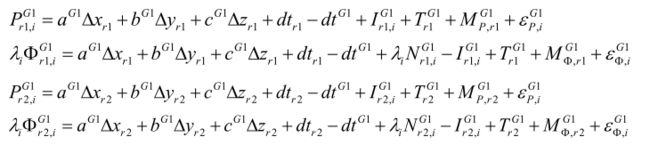
两个接收机的观测方程里，当两个接收机距离较近时，卫星端钟差、电离层和对流层延迟误差十分相近，两个接收机的观测方程做差：

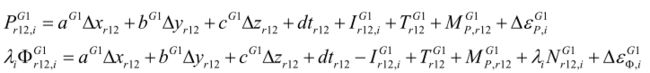
其中

因此，卫星钟差消除，电离层、对流层误差削弱。

2）星间做差

对两个接收机同时观测到的卫星G2观测方程站间做差，得到：

再对G1和G2两颗卫星的单差观测方程再一次星间做差，进一步消除了接收机端钟差，进一步削弱了电离层和对流层误差：

其中

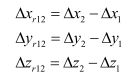
当两个接收机距离较近，即短基线情况下，电离层误差和对流层误差经过双差可消除：

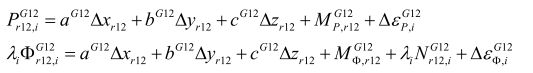
通过上述操作，双差观测方程中误差量被消除，仅剩待求的基线向量$(△x_{12},△y_{12},△z_{12})$和载波相位中的双差模糊度$N_{r12,i}^{G12}$.

e.浮点解

假设当前时刻两个接收机同时观测到M颗卫星，以G1为参考星，可以列出观测方程组

参数求解得到基线向量和双差模糊度结果，此时得到的结果均为浮点解，并未将载波相位观测值的优势完全发挥，精度较差，因此进一步对双差模糊度进行整数固定。

f.模糊度固定

基于上述浮点解的结果，进行模糊度固定，载波相位观测方程可以表示为

先求解整数模糊度N, 整数模糊度回代到载波相位观测方程，重新解得基线向量 $(△x_{12},△y_{12},△z_{12})$ 的固定解。

具体可以参考：https://blog.csdn.net/qq_41782151/article/details/121017678

四、 定向结果及精度

基本思想：设备副天线与主天线做差分可以得到副天线相对主天线的相对位置，进而可以计算航向和Roll角。

根据卫星观测解算出的基线向量$(△x_{12},△y_{12},△z_{12})$ 是ECEF坐标系下的相对位置，根据坐标系旋转矩阵变换到当地水平坐标系NED系下，变换矩阵为：

因此基线矢量在当地水平坐标系下的坐标为 $b^l=C_e^l{x}^e$

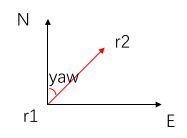
双天线基线与Vehicle的载体坐标系y轴平行（安装保证），因此其航向角为：

双天线定向退出或无法进入固定解，可能是其中一路天线观测卫星较少或观测受到干扰、信号质量较差。通常固定解时yaw求解精度比较准确，最终定位精度与基线长度有关，通常精度<1°（0.1-0.3°/基线长度）。

五、定位结果及精度

基本思想：设备与基站的数据差分实现厘米的实时定位。根据ECEF坐标系下的相对位置，加上基站位置，解算出ECEF坐标系下的绝对位置。

根据卫星观测解算出的基线向量$(△x_{12},△y_{12},△z_{12})$以及差分数据中基站的位置$(x_0,y_0,z_0)$（基站位置固定，因此$△x_1=0$,$△x_2=x_{r2}-x_0$），可以得到绝对位置$x_{r2}=[x,y,z]=[x_0,y_0,z_0]+[(△x_{12},△y_{12},△z_{12}]$。通常RTK定位精度为cm级（1-3cm）。

基站需要通过云端等设备将差分数据发送给接收机，这样接收机才能进行双差高精定位，当然，并非所有场景都能进入固定解，浮点解的结果也可以使用，只不过精度差一些。