python时间序列分析2-平稳时间序列分析
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
数据预处理
data = pd.read_csv('./data/catfish.csv',parse_dates=[0],squeeze=True,index_col= 0)
data.head(3)
Date
1986-01-01 9034
1986-02-01 9596
1986-03-01 10558
Name: Total, dtype: int64
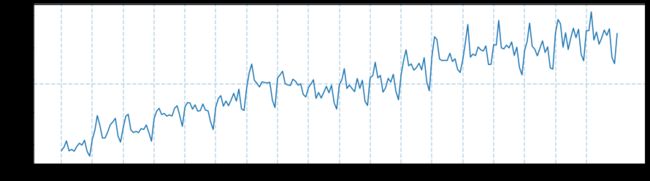
绘制时序图(判断平稳性)
plt.figure(figsize=(15,4))
plt.plot(data['1986-01-01':'2004-01-01'])
for year in range(1986,2004):
plt.axvline(pd.to_datetime(str(year)+'-01-01'),linestyle = '--',alpha = 0.3)
plt.axhline(data['1986-01-01':'2004-01-01'].mean(),alpha=0.3,linestyle='--')
plt.show()
时间序列呈现明显的上升趋势和周期性,因此是不平稳时间序列
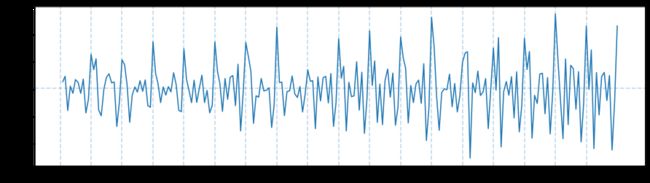
差分处理
# 一阶差分
data_diff = data.diff()[1:]
plt.figure(figsize=(15,4))
plt.plot(data_diff['1986-01-01':'2004-01-01'])
for year in range(1986,2004):
plt.axvline(pd.to_datetime(str(year)+'-01-01'),linestyle = '--',alpha = 0.3)
plt.axhline(data_diff['1986-01-01':'2004-01-01'].mean(),alpha=0.3,linestyle='--')
plt.show()
可以看到时间序列在0均值上下移动,可认为平稳
白噪声检验
from statsmodels.stats.diagnostic import acorr_ljungbox
df = acorr_ljungbox(data_diff,lags=[6,12,18],return_df=True,boxpierce = True)
df
| lb_stat | lb_pvalue | bp_stat | bp_pvalue | |
|---|---|---|---|---|
| 6 | 95.719733 | 1.957855e-18 | 94.002129 | 4.460230e-18 |
| 12 | 373.541488 | 1.498233e-72 | 360.830939 | 7.259069e-70 |
| 18 | 466.300398 | 1.243989e-87 | 448.452496 | 6.846258e-84 |
LB检验和Q检验的P值都远小于0.05,可以认为此序列不是白噪声序列
选择ARMA模型
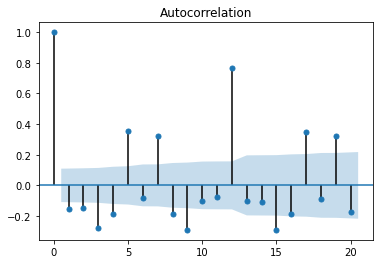
绘制自相关图
from statsmodels.graphics.tsaplots import plot_acf
plot_acf(data_diff,alpha=0.05,lags=20)
不具有截尾性,因此选择MA(0)或MA(1)
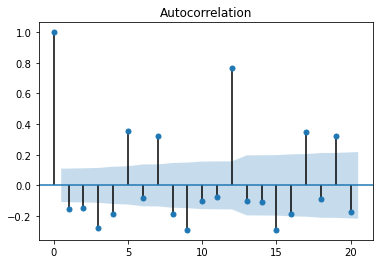
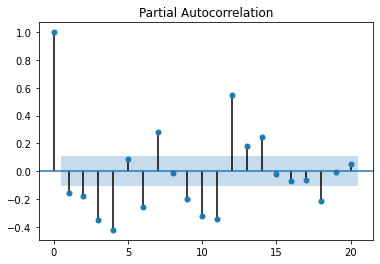
绘制偏自相关系数
from statsmodels.graphics.tsaplots import plot_pacf
plot_pacf(data_diff,alpha=0.05,lags=20)
近似4阶截尾,选择AR(4)模型
划分数据集
train_end = pd.to_datetime('2003-07-01')
test_end = pd.to_datetime('2004-07-01')
train_data = data_diff[:train_end]
test_data = data_diff[train_end+pd.Timedelta(days = 1):test_end]
AR模型
from statsmodels.tsa.ar_model import AR
import time
model1 = AR(train_data,freq='MS')
start = time.time()
model1_fit = model1.fit(max_lag = 4)
end = time.time()
print('Model Fitting Time:', end - start)
Model Fitting Time: 0.009086370468139648
print(model1_fit.summary())
AR Model Results
==============================================================================
Dep. Variable: T - o t
Model: AR(14) Log Likelihood -1614.336
Method: cmle S.D. of innovations 913.668
Date: Thu, 01 Apr 2021 AIC 13.798
Time: 10:29:29 BIC 14.066
Sample: 02-01-1986 HQIC 13.907
- 07-01-2003
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 192.0433 90.030 2.133 0.033 15.587 368.499
L1.Total -0.4668 0.072 -6.461 0.000 -0.608 -0.325
L2.Total -0.4105 0.077 -5.318 0.000 -0.562 -0.259
L3.Total -0.2621 0.069 -3.787 0.000 -0.398 -0.126
L4.Total -0.2194 0.071 -3.071 0.002 -0.359 -0.079
L5.Total -0.1355 0.072 -1.880 0.060 -0.277 0.006
L6.Total -0.2207 0.071 -3.105 0.002 -0.360 -0.081
L7.Total -0.0990 0.072 -1.375 0.169 -0.240 0.042
L8.Total -0.1737 0.072 -2.403 0.016 -0.315 -0.032
L9.Total -0.2368 0.071 -3.314 0.001 -0.377 -0.097
L10.Total -0.1644 0.073 -2.253 0.024 -0.307 -0.021
L11.Total -0.1564 0.072 -2.161 0.031 -0.298 -0.015
L12.Total 0.6155 0.071 8.634 0.000 0.476 0.755
L13.Total 0.2541 0.079 3.224 0.001 0.100 0.409
L14.Total 0.1846 0.075 2.457 0.014 0.037 0.332
Roots
==============================================================================
Real Imaginary Modulus Frequency
------------------------------------------------------------------------------
AR.1 0.8839 -0.5102j 1.0206 -0.0833
AR.2 0.8839 +0.5102j 1.0206 0.0833
AR.3 1.1629 -0.0000j 1.1629 -0.0000
AR.4 0.5001 -0.8689j 1.0026 -0.1669
AR.5 0.5001 +0.8689j 1.0026 0.1669
AR.6 0.0021 -1.0224j 1.0224 -0.2497
AR.7 0.0021 +1.0224j 1.0224 0.2497
AR.8 -1.0331 -0.0000j 1.0331 -0.5000
AR.9 -0.8696 -0.5052j 1.0057 -0.4162
AR.10 -0.8696 +0.5052j 1.0057 0.4162
AR.11 -0.5194 -0.9276j 1.0631 -0.3312
AR.12 -0.5194 +0.9276j 1.0631 0.3312
AR.13 -0.7503 -1.7439j 1.8985 -0.3147
AR.14 -0.7503 +1.7439j 1.8985 0.3147
------------------------------------------------------------------------------
所以模型是 x t = 192.0433 − 0.4668 x t − 1 − 0.4105 x t − 2 . . . x_t = 192.0433-0.4668x_{t-1}-0.4105x_{t-2}... xt=192.0433−0.4668xt−1−0.4105xt−2...
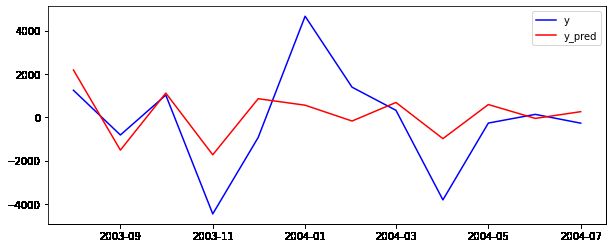
查看预测结果
#起始点、终止点
pred_start_date = test_data.index[0]
pred_end_date = test_data.index[-1]
#预测值和残差
predictions = model1_fit.predict(start=pred_start_date, end=pred_end_date)
residuals = test_data - predictions
plt.figure(figsize=(10,4))
plt.plot(test_data,label = 'y',color = 'b')
plt.plot(predictions,label = 'y_pred',color = 'r')
plt.legend()
plt.show()
ARMA模型
from statsmodels.tsa.arima_model import ARMA
model2 = ARMA(train_data,freq='MS',order = (4,1))
start = time.time()
model2_fit = model2.fit()
end = time.time()
print('Model Fitting Time:', end - start)
Model Fitting Time: 0.7675204277038574
model2_fit.summary()
| Dep. Variable: | Total | No. Observations: | 210 |
|---|---|---|---|
| Model: | ARMA(4, 1) | Log Likelihood | -1835.240 |
| Method: | css-mle | S.D. of innovations | 1505.051 |
| Date: | Thu, 01 Apr 2021 | AIC | 3684.480 |
| Time: | 10:52:30 | BIC | 3707.910 |
| Sample: | 02-01-1986 | HQIC | 3693.952 |
| - 07-01-2003 |
| coef | std err | z | P>|z| | [0.025 | 0.975] | |
|---|---|---|---|---|---|---|
| const | 85.2394 | 48.166 | 1.770 | 0.077 | -9.163 | 179.642 |
| ar.L1.Total | -0.8138 | 0.086 | -9.459 | 0.000 | -0.982 | -0.645 |
| ar.L2.Total | -0.4284 | 0.071 | -6.055 | 0.000 | -0.567 | -0.290 |
| ar.L3.Total | -0.5665 | 0.070 | -8.075 | 0.000 | -0.704 | -0.429 |
| ar.L4.Total | -0.5620 | 0.058 | -9.620 | 0.000 | -0.676 | -0.447 |
| ma.L1.Total | 0.5534 | 0.090 | 6.149 | 0.000 | 0.377 | 0.730 |
| Real | Imaginary | Modulus | Frequency | |
|---|---|---|---|---|
| AR.1 | 0.4829 | -1.0659j | 1.1702 | -0.1823 |
| AR.2 | 0.4829 | +1.0659j | 1.1702 | 0.1823 |
| AR.3 | -0.9870 | -0.5704j | 1.1399 | -0.4166 |
| AR.4 | -0.9870 | +0.5704j | 1.1399 | 0.4166 |
| MA.1 | -1.8071 | +0.0000j | 1.8071 | 0.5000 |
predictions = model2_fit.predict(start=pred_start_date, end=pred_end_date)
residuals = test_data - predictions
plt.figure(figsize=(10,4))
plt.plot(test_data,label = 'y',color = 'b')
plt.plot(predictions,label = 'y_pred',color = 'r')
plt.legend()
plt.show()
模型比较
model1_fit.aic,model2_fit.aic
(13.798200287066459, 3684.480163721421)
可以看到AR(14)的模型AIC显著小于ARMA(4,1)模型,因此选择AR(14)模型
模型检验
print(model1_fit.pvalues)
const 3.291656e-02
L1.Total 1.039287e-10
L2.Total 1.049426e-07
L3.Total 1.527589e-04
L4.Total 2.133285e-03
L5.Total 6.012763e-02
L6.Total 1.900197e-03
L7.Total 1.690425e-01
L8.Total 1.626242e-02
L9.Total 9.182977e-04
L10.Total 2.423953e-02
L11.Total 3.070085e-02
L12.Total 5.932908e-18
L13.Total 1.264368e-03
L14.Total 1.399151e-02
dtype: float64
model1_fit.pvalues>0.05
const False
L1.Total False
L2.Total False
L3.Total False
L4.Total False
L5.Total True
L6.Total False
L7.Total True
L8.Total False
L9.Total False
L10.Total False
L11.Total False
L12.Total False
L13.Total False
L14.Total False
dtype: bool
L5和L7参数不符合显著性要求,所以应该删除掉