LMDI 理论推导详解【从理论到Python-MATLAB实现(理论)】
LMDI 理论推导详解【从理论到Python-MATLAB实现(理论)】
影响因素分解分析方法能够有效地反映任意时段上各个影响因素对目标变量变化的影响程度
大多数模型虽然可以定量反映各影响因素对目标变量变化的影响程度,但无法解释其任意时段上各个影响因素对目标变量变化的影响程度。因此,给分析结果带来了巨大的缺陷,同时使后续分析难以进一步开展。
分解分析将一个待分解的研究目标(如能源消耗、碳排放总量/强度等)通过定性的方法分解为若干驱动因素的集合,然后通过定量去研究这些因素对该研究目标的影响程度大小,即贡献水平。
- 结构分解
- 指数分解
计算过程清晰、计算方法简便,能够很好兼容分解后影响因素少的问题,适用于时间序列分析的模型
1. 指数分解的基本形式
设 V V V为m个部门之后,即 V = ∑ i V i V=\sum_i{V_i} V=∑iVi,在n维空间里,目标量V可以分解成n个影响因素的成绩,记为 V i = x 1 , i x 2 , i ⋯ x n , i V_{i}=x_{1, i} x_{2, i} \cdots x_{n, i} Vi=x1,ix2,i⋯xn,i。在时间周期 [ 0 , T ] [0,T] [0,T]内,目标量从 V 0 = ∑ i x 1 , i 0 x 2 , i 0 ⋯ x n , i 0 V^{0}=\sum_{i} x_{1, i}^{0} x_{2, i}^{0} \cdots x_{n, i}^{0} V0=∑ix1,i0x2,i0⋯xn,i0变化到 V T = ∑ i x 1 , i T x 2 , i T ⋯ x n , i T V^{T}=\sum_{i} x_{1, i}^{T} x_{2, i}^{T} \cdots x_{n, i}^{T} VT=∑ix1,iTx2,iT⋯xn,iT
乘法形式(Multiplicative Decomposition)
D tot = V T / V 0 = D x 1 D x 2 ⋯ D x n D rsd ) (1-1) \left.D_{\text {tot}}=V^{T} / V^{0}=D_{x_{1}} D_{x_{2}} \cdots D_{x_{n}} D_{\text {rsd }}\right)\tag{1-1} Dtot=VT/V0=Dx1Dx2⋯DxnDrsd )(1-1)
加法形式(Additive Decomposition)
Δ V tot = V T − V 0 = Δ V x 1 + Δ V x 2 + ⋯ + Δ V x n + Δ V r s d (1-2) \Delta V_{\text {tot}}=V^{T}-V^{0}=\Delta V_{x_{1}}+\Delta V_{x_{2}}+\cdots+\Delta V_{x_{n}}+\Delta V_{r s d}\tag{1-2} ΔVtot=VT−V0=ΔVx1+ΔVx2+⋯+ΔVxn+ΔVrsd(1-2)
指数分解分析中的Laspeyres 和 Divisia 方法应用较为普遍。
1.1 Laspeyres 分解法(Laspeyres Index Decomposition)
由德国学者Laspeyres 于1864年提出的,当时主要用于解决一些经济问题,比如产品产量变化和价格变化各自对企业销售额的影响。拉氏指数法是假定其他因素不变,直接对各个因素进行微分,从二分求出某一因素的变化对被分解变量的影响,该方法简便直观、易于理解,是最为常见的一种分解方法。
1.2 Divisa 分解法(Divisia Index Decomposition)
由法国数学家Divisia于1924年提出,这种方法的宗旨:将分解出的各个因素看成是时间t的连续可微函数,对时间 t t t进行微分,然后分解出各个因素的变化对被分解变量的影响。
2. LMDI指数分解分析
根据Divisia分解法定义,目标变量V对时间进行微分:
d V t / d t = ∑ k ∑ i x 1 , i t x 2 , i t ⋯ x k − 1 , i t x k + 1 , i t ⋯ x n , i t d x k , i t / d t = ∑ k ∑ i V i t d ( ln x k , i t ) / d t (2-1) d V^{t} / d t= \\ \sum_{k} \sum_{i} x_{1, i}^{t} x_{2, i}^{t} \cdots x_{k-1, i}^{t} x_{k+1, i}^{t} \cdots x_{n, i}^{t} d x_{k, i}^{t} / d t \\ =\sum_{k} \sum_{i} V_{i}^{t} d\left(\ln x_{k, i}^{t}\right) / d t\tag{2-1} dVt/dt=k∑i∑x1,itx2,it⋯xk−1,itxk+1,it⋯xn,itdxk,it/dt=k∑i∑Vitd(lnxk,it)/dt(2-1)
上式等式两边同时对时间进行积分:
∫ 0 T d V t / d t = V T − V 0 = ∑ k ∫ 0 T ∑ i V i t d ( ln x k , i t ) / d t (2-2) \int_{0}^{T} d V^{t} / d t=V^{T}-V^{0}=\sum_{k} \int_{0}^{T} \sum_{i} V_{i}^{t} d\left(\ln x_{k, i}^{t}\right) / d t\tag{2-2} ∫0TdVt/dt=VT−V0=k∑∫0Ti∑Vitd(lnxk,it)/dt(2-2)
根据指数分解加法形式有:
Δ V x k = ∫ 0 T ∑ i V i t d ( ln x k , i t ) / d t (2-3) \Delta V_{x_{k}}=\int_{0}^{T} \sum_{i} V_{i}^{t} d\left(\ln x_{k, i}^{t}\right) / d t\tag{2-3} ΔVxk=∫0Ti∑Vitd(lnxk,it)/dt(2-3)
等式 (2-1) 两边同时除以 V t V^t Vt, 并对时间 t t t进行积分:
∫ 0 T 1 V t d V t / d t = ln ( V T / V 0 ) = ∑ k ∫ 0 T ∑ i ω i t d ( ln x k , i t ) / d t (2-4) \int_{0}^{T} \frac{1}{V^{t}} d V^{t} / d t=\ln \left(V^{T} / V^{0}\right)=\\ \sum_{k} \int_{0}^{T} \sum_{i} \omega_{i}^{t} d\left(\ln x_{k, i}^{t}\right) / d t\tag{2-4} ∫0TVt1dVt/dt=ln(VT/V0)=k∑∫0Ti∑ωitd(lnxk,it)/dt(2-4)
上市两边同时做 e e e 的指数运算,根据指数分解乘法形式,则有:
D x k = exp { ∫ 0 T ∑ i ω i t d ( ln x k , i t ) / d t } (2-5) D_{x_{k}}=\exp \left\{\int_{0}^{T} \sum_{i} \omega_{i}^{t} d\left(\ln x_{k, i}^{t}\right) / d t\right\}\tag{2-5} Dxk=exp{∫0Ti∑ωitd(lnxk,it)/dt}(2-5)
2.1 AMDI方法
由于前面的加法和乘法计算困难,因此通常采用近似计算。根据近似方法不同又产生了多种具体的分解结果,即不同类型的 Divisia 分解法,例如 AMDI
算术平均迪氏指数法 (Arithmetic Mean Index Method,AMDI)
加法形式
Δ V x k = 0.5 ∑ i ( V i 0 + V i T ) ln ( x k , i T / x k , i o ) (2-6) \Delta V_{x_{k}}=0.5 \sum_{i}\left(V_{i}^{0}+V_{i}^{T}\right) \ln \left(x_{k, i}^{T} / x_{k, i}^{o}\right)\tag{2-6} ΔVxk=0.5i∑(Vi0+ViT)ln(xk,iT/xk,io)(2-6)
乘法形式
D x k = exp { ∑ i 0.5 ( ω i 0 + ω i T ) ln ( x k , i T / x k , i o ) } (2-7) D_{x_{k}}=\exp \left\{\sum_{i} 0.5\left(\omega_{i}^{0}+\omega_{i}^{T}\right) \ln \left(x_{k, i}^{T} / x_{k, i}^{o}\right)\right\}\tag{2-7} Dxk=exp{i∑0.5(ωi0+ωiT)ln(xk,iT/xk,io)}(2-7)
2.2 LMDI 方法
AMDI分解法也存在残值问题,Ang等研究提出了对数平均迪氏指数法,对AMDI方法进行了改进。LMDI分解模型如下:
对数平均迪氏指数法 (Logarithmic Mean Index Method, LMDI)
加法形式
Δ V x k = ∑ i L ( V i T , V i 0 ) ln ( x k , i T / x k , i o ) (2-8) \Delta V_{x_{k}}=\sum_{i} L\left(V_{i}^{T}, V_{i}^{0}\right) \ln \left(x_{k, i}^{T} / x_{k, i}^{o}\right)\tag{2-8} ΔVxk=i∑L(ViT,Vi0)ln(xk,iT/xk,io)(2-8)
乘法形式
D x i = exp { ∑ i L ( V i T , V i 0 ) L ( V T , V 0 ) ln ( x k , i T / x k , i o ) } = exp { Δ V x i L ( V T , V 0 ) } (2-9) D_{x_{i}}=\exp \left\{\sum_{i} \frac{L\left(V_{i}^{T}, V_{i}^{0}\right)}{L\left(V^{T}, V^{0}\right)} \ln \left(x_{k, i}^{T} / x_{k, i}^{o}\right)\right\}= \\ \exp \left\{\frac{\Delta V_{x_{i}}}{L\left(V^{T}, V^{0}\right)}\right\}\tag{2-9} Dxi=exp{i∑L(VT,V0)L(ViT,Vi0)ln(xk,iT/xk,io)}=exp{L(VT,V0)ΔVxi}(2-9)
其中: L ( x , y ) = ( y − x ) / ln ( y / x ) L(x, y)=(y-x) / \ln (y / x) L(x,y)=(y−x)/ln(y/x)
3. LMDI指数分解分析:案例展示
利用LMDI方法,对“I=PAT”模型进行因素分解,结果如下
对数平均迪氏指数法(Logarithmic Mean Index Method, LMDI)
Δ I P = ( I T − I ∘ ) ln ( I T / I 0 ) ln ( P T / P 0 ) Δ I A = ( I T − I 0 ) ln ( I T / I 0 ) ln ( A T / A 0 ) Δ I T = ( I T − I 0 ) ln ( I T / I 0 ) ln ( T T / T 0 ) (3-1) \begin{aligned} \Delta I_{P} &=\frac{\left(I^{T}-I^{\circ}\right)}{\ln \left(I^{T} / I^{0}\right)} \ln \left(P^{T} / P^{0}\right) \\ \Delta I_{A} &=\frac{\left(I^{T}-I^{0}\right)}{\ln \left(I^{T} / I^{0}\right)} \ln \left(A^{T} / A^{0}\right) \\ \Delta I_{T} &=\frac{\left(I^{T}-I^{0}\right)}{\ln \left(I^{T} / I^{0}\right)} \ln \left(T^{T} / T^{0}\right) \end{aligned}\tag{3-1} ΔIPΔIAΔIT=ln(IT/I0)(IT−I∘)ln(PT/P0)=ln(IT/I0)(IT−I0)ln(AT/A0)=ln(IT/I0)(IT−I0)ln(TT/T0)(3-1)
可以证明LMDI方法是一种完全分解方法
Δ I P + Δ I A + Δ I T = ( I T − I 0 ) ln ( I T / I 0 ) [ ln ( P T / P 0 ) + ln ( A T / A 0 ) + ln ( T T / T 0 ) ] = ( I T − I 0 ) ln ( I T / I 0 ) ln ( P T A T T T / P 0 A 0 T 0 ) = I T − I 0 (3-2) \begin{array}{l} \Delta I_{P}+\Delta I_{A}+\Delta I_{T} =\frac{\left(I^{T}-I^{0}\right)}{\ln \left(I^{T} / I^{0}\right)}\left[\ln \left(P^{T} / P^{0}\right)+\ln \left(A^{T} / A^{0}\right)+\ln \left(T^{T} / T^{0}\right)\right]\\ =\frac{\left(I^{T}-I^{0}\right)}{\ln \left(I^{T} / I^{0}\right)} \ln \left(P^{T} A^{T} T^{T} / P^{0} A^{0} T^{0}\right) =I^{T}-I^{0} \end{array} \tag{3-2} ΔIP+ΔIA+ΔIT=ln(IT/I0)(IT−I0)[ln(PT/P0)+ln(AT/A0)+ln(TT/T0)]=ln(IT/I0)(IT−I0)ln(PTATTT/P0A0T0)=IT−I0(3-2)
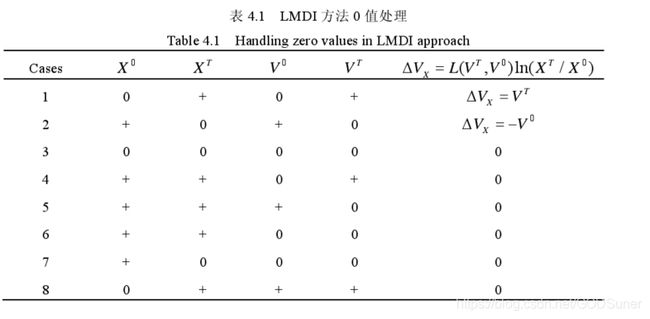
4. LMDI的“零值”处理
对于 Δ V x = L ( V T , V 0 ) ln ( X T / X 0 ) \Delta V_{x}=L\left(V^{T}, V^{0}\right) \ln \left(X^{T} / X^{0}\right) ΔVx=L(VT,V0)ln(XT/X0), 如果其中任意一个变量趋近于0时:
其对数运算值趋近于无穷。B.W.Ang 等人讨论了以下8类情况
5. LMDI的补充
研究人员和政府决策者采用的有关能源消费及碳排放影响因素的分解分析方法很多,但具体哪一种更好没有一致的认识。Ang (2004) 收集了一些常用的方法,对比之后认为不论是从理论背景、实用性、可操行还是结果表达的角度,LMDI都是一种极好的分解方法。同时,LMDI方法没有残差,而且能够处理出现零值的情况。
指数分解方法对分析数据以两种方式分解:时间序列分解(time-series)方式和区间分解(period-wise)方式。
- 时间序列分解:分t年和t+1年进行,如2005-2006,2006-2007和2007-2008-
- 区间分解:对两个基准年之间的变化进行的,而中间年份的变化忽略不计。
6。 参考文献
Xiang X, Ma X, Ma Z, et al. Python-LMDI: A Tool for Index Decomposition Analysis of Building Carbon Emissions[J]. Buildings, 2022, 12(1): 83.