Java根据坐标经纬度计算两点距离(5种方法)、校验经纬度是否在圆/多边形区域内的算法推荐
目录
前言
一、根据坐标经纬度计算两点距离(5种方法)
1.方法一
2.方法二
3.方法三
4.方法四
5.方法五
5.1 POM引入第三方依赖
5.2 代码
6.测试结果对比
二、校验经纬度是否在制定区域内
1.判断一个坐标是否在圆形区域内
2.判断一个坐标是否在一个多边形区域内
3.结果
总结
前言
在开发项目中会用到根据两点坐标计算之间距离的算法,网上也找了很多的方法,多多少少会存在一些问题的。以下方法已经在我本地运行通过,利用百度地图拾取坐标系统和百度地图测距工具进行测试,现将其整理了一下。以供大家参考:
一、根据坐标经纬度计算两点距离
1.方法一
package com.test.java.util;
/**
* 坐标位置相关util
*/
public class PositionUtil {
/**
* 赤道半径(单位:米)
*/
private static final double EQUATOR_RADIUS = 6378137;
/**
* 方法一:(反余弦计算方式)
*
* @param longitude1 第一个点的经度
* @param latitude1 第一个点的纬度
* @param longitude2 第二个点的经度
* @param latitude2 第二个点的纬度
* @return 返回距离,单位m
*/
public static double getDistance1(double longitude1, double latitude1, double longitude2, double latitude2) {
// 纬度
double lat1 = Math.toRadians(latitude1);
double lat2 = Math.toRadians(latitude2);
// 经度
double lon1 = Math.toRadians(longitude1);
double lon2 = Math.toRadians(longitude2);
// 纬度之差
double a = lat1 - lat2;
// 经度之差
double b = lon1 - lon2;
// 计算两点距离的公式
double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(lat1) * Math.cos(lat2) * Math.pow(Math.sin(b / 2), 2)));
// 弧长乘赤道半径, 返回单位: 米
s = s * EQUATOR_RADIUS;
return s;
}
}
2.方法二
package com.test.java.util;
/**
* 坐标位置相关util
*/
public class PositionUtil {
/**
* 地球平均半径(单位:米)
*/
private static final double EARTH_AVG_RADIUS = 6371000;
/**
* 方法二:(反余弦计算方式)
*
* @param longitude1 第一点的经度
* @param latitude1 第一点的纬度
* @param longitude2 第二点的经度
* @param latitude2 第二点的纬度
* @return 返回的距离,单位m
*/
public static double getDistance3(double longitude1, double latitude1, double longitude2, double latitude2) {
// 经纬度(角度)转弧度。弧度作为作参数,用以调用Math.cos和Math.sin
// A经弧度
double radiansAX = Math.toRadians(longitude1);
// A纬弧度
double radiansAY = Math.toRadians(latitude1);
// B经弧度
double radiansBX = Math.toRadians(longitude2);
// B纬弧度
double radiansBY = Math.toRadians(latitude2);
// 公式中“cosβ1cosβ2cos(α1-α2)+sinβ1sinβ2”的部分,得到∠AOB的cos值
double cos = Math.cos(radiansAY) * Math.cos(radiansBY) * Math.cos(radiansAX - radiansBX) + Math.sin(radiansAY) * Math.sin(radiansBY);
// System.out.println("cos = " + cos); // 值域[-1,1]
// 反余弦值
double acos = Math.acos(cos);
// System.out.println("acos = " + acos); // 值域[0,π]
// System.out.println("∠AOB = " + Math.toDegrees(acos)); // 球心角 值域[0,180]
// 最终结果
return EARTH_AVG_RADIUS * acos;
}
}
3.方法三
基于谷歌地图的计算公式计算距离
package com.test.java.util;
/**
* 坐标位置相关util
*/
public class PositionUtil {
/**
* 地球平均半径(单位:米)
*/
private static final double EARTH_AVG_RADIUS = 6371000;
/**
* 经纬度转化为弧度(rad)
*
* @param d 经度/纬度
*/
private static double rad(double d) {
return d * Math.PI / 180.0;
}
/**
* 方法三:(基于googleMap中的算法得到两经纬度之间的距离,计算精度与谷歌地图的距离精度差不多。)
*
* @param longitude1 第一点的经度
* @param latitude1 第一点的纬度
* @param longitude2 第二点的经度
* @param latitude2 第二点的纬度
* @return 返回的距离,单位m
*/
public static double getDistance2(double longitude1, double latitude1, double longitude2, double latitude2) {
double radLat1 = rad(latitude1);
double radLat2 = rad(latitude2);
double a = radLat1 - radLat2;
double b = rad(longitude1) - rad(longitude2);
double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(radLat1) * Math.cos(radLat2) * Math.pow(Math.sin(b / 2), 2)));
s = s * EARTH_AVG_RADIUS;
s = Math.round(s * 10000d) / 10000d;
return s;
}
}
4.方法四
基于高德地图
package com.test.java.util;
/**
* 计算距离
*/
public class PositionUtil {
/**
* 方法四:(高德地图计算方法)
*
* @param longitude1 第一点的经度
* @param latitude1 第一点的纬度
* @param longitude2 第二点的经度
* @param latitude2 第二点的纬度
* @return 返回的距离,单位m
*/
public static Double getDistance4(double longitude1, double latitude1, double longitude2, double latitude2) {
if (longitude1 == 0 || latitude1 == 0 || latitude2 == 0 || longitude2 == 0) {
return -1.0;
}
longitude1 *= 0.01745329251994329;
latitude1 *= 0.01745329251994329;
longitude2 *= 0.01745329251994329;
latitude2 *= 0.01745329251994329;
double var1 = Math.sin(longitude1);
double var2 = Math.sin(latitude1);
double var3 = Math.cos(longitude1);
double var4 = Math.cos(latitude1);
double var5 = Math.sin(longitude2);
double var6 = Math.sin(latitude2);
double var7 = Math.cos(longitude2);
double var8 = Math.cos(latitude2);
double[] var10 = new double[3];
double[] var20 = new double[3];
var10[0] = var4 * var3;
var10[1] = var4 * var1;
var10[2] = var2;
var20[0] = var8 * var7;
var20[1] = var8 * var5;
var20[2] = var6;
return Math.asin(Math.sqrt((var10[0] - var20[0]) * (var10[0] - var20[0]) + (var10[1] - var20[1]) * (var10[1] - var20[1]) + (var10[2] - var20[2]) * (var10[2] - var20[2])) / 2.0) * 1.27420015798544E7;
// 结果四舍五入 保留2位小数
//return new BigDecimal(distance).setScale(2, RoundingMode.HALF_UP).doubleValue();
}
}
5.方法五
该方法是利用第三方jar包计算
5.1 POM引入第三方依赖
org.gavaghan
geodesy
1.1.3
5.2 代码
package com.test.java.util;
import org.gavaghan.geodesy.Ellipsoid;
import org.gavaghan.geodesy.GeodeticCalculator;
import org.gavaghan.geodesy.GeodeticCurve;
import org.gavaghan.geodesy.GlobalCoordinates;
/**
* 坐标位置相关util
*/
public class PositionUtil {
/**
* 方法四:(利用第三方jar包计算)
* 计算两个经纬度之间的距离
*
* @param longitude1 第一点的经度
* @param latitude1 第一点的纬度
* @param longitude2 第二点的经度
* @param latitude2 第二点的纬度
* @param ellipsoid 计算方式
* @return 返回的距离,单位m
*/
public static double getDistance4(double longitude1, double latitude1, double longitude2, double latitude2, Ellipsoid ellipsoid) {
// 创建GeodeticCalculator,调用计算方法,传入坐标系、经纬度用于计算距离
GlobalCoordinates firstPoint = new GlobalCoordinates(latitude1, longitude1);
GlobalCoordinates secondPoint = new GlobalCoordinates(latitude2, longitude2);
GeodeticCurve geoCurve = new GeodeticCalculator().calculateGeodeticCurve(ellipsoid, firstPoint, secondPoint);
return geoCurve.getEllipsoidalDistance();
}
}
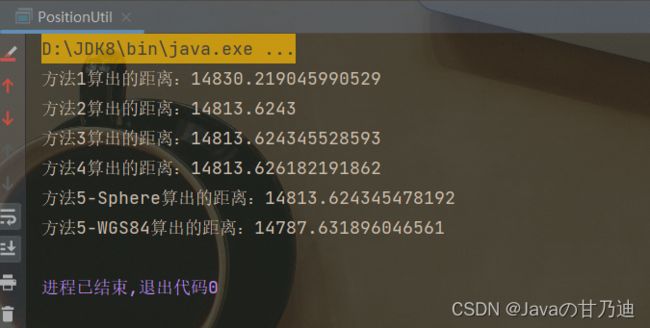
6.测试结果对比
这里我直接一起调用者4种方法,这样看结果也更加直观些。
public static void main(String[] args) {
double longitude1 = 117.344733;
double latitude1 = 31.912334;
double longitude2 = 117.272186;
double latitude2 = 31.79422;
double distance1 = PositionUtil.getDistance1(longitude1, latitude1, longitude2, latitude2);
double distance2 = PositionUtil.getDistance2(longitude1, latitude1, longitude2, latitude2);
double distance3 = PositionUtil.getDistance3(longitude1, latitude1, longitude2, latitude2);
double distance4 = PositionUtil.getDistance4(longitude1, latitude1, longitude2, latitude2);
double distance5 = PositionUtil.getDistance4(longitude1, latitude1, longitude2, latitude2, Ellipsoid.Sphere);
double distance6 = PositionUtil.getDistance4(longitude1, latitude1, longitude2, latitude2, Ellipsoid.WGS84);
System.out.println("方法1算出的距离:" + distance1);
System.out.println("方法2算出的距离:" + distance2);
System.out.println("方法3算出的距离:" + distance3);
System.out.println("方法4算出的距离:" + distance4);
System.out.println("方法4-Sphere算出的距离:" + distance5);
System.out.println("方法4-WGS84算出的距离:" + distance6);
}
可以看出,这几个方法算出的距离误差相对较小。而且main方法中提供的测试数据也是我自身的真实数据,结合百度地图的测距工具进行的测试。有需要的小伙伴,可以自行选择合适的方法。
二、校验经纬度是否在制定区域内
怎么样判断一个坐标点在指定的区域内?其中区域又会分为:圆,多边形和不规则的多边形。
1.判断一个坐标是否在圆形区域内
计算这个坐标点和圆心之间的距离,然后跟圆的半径进行比较,如果比半径大,就不在圆形区域内,如果小于等于圆的半径,则该坐标点在圆形区域内。
package com.test.java.util;
import org.apache.commons.lang3.StringUtils;
/**
* 计算距离
*/
public class PositionUtil {
/**
* 赤道半径(单位:米)
*/
private static final double EQUATOR_RADIUS = 6378137;
/**
* 方法一:(反余弦计算方式)
*
* @param longitude1 第一个点的经度
* @param latitude1 第一个点的纬度
* @param longitude2 第二个点的经度
* @param latitude2 第二个点的纬度
* @return 返回距离,单位m
*/
public static double getDistance1(double longitude1, double latitude1, double longitude2, double latitude2) {
// 纬度
double lat1 = Math.toRadians(latitude1);
double lat2 = Math.toRadians(latitude2);
// 经度
double lon1 = Math.toRadians(longitude1);
double lon2 = Math.toRadians(longitude2);
// 纬度之差
double a = lat1 - lat2;
// 经度之差
double b = lon1 - lon2;
// 计算两点距离的公式
double s = 2 * Math.asin(Math.sqrt(Math.pow(Math.sin(a / 2), 2) + Math.cos(lat1) * Math.cos(lat2) * Math.pow(Math.sin(b / 2), 2)));
// 弧长乘赤道半径, 返回单位: 米
s = s * EQUATOR_RADIUS;
return s;
}
/**
* 判断坐标点是否在圆形区域内
* 计算这个坐标点和圆心点之间的距离,然后跟圆的半径进行比较,如果比半径大,就不在圆形区域内,如果小于等于圆的半径,则该坐标点在圆形区域内
*
* @param longitude1 第一点的经度
* @param latitude1 第一点的纬度
* @param longitude2 第二点的经度
* @param latitude2 第二点的纬度
* @param radius 圆形范围半径(单位:米)
* @return true:不在区域内; false:在区域内
*/
public static boolean isInCircle(double longitude1, double latitude1, double longitude2, double latitude2, String radius) {
if (StringUtils.isBlank(radius)) {
throw new RuntimeException("请输入范围半径");
}
return getDistance1(longitude1, latitude1, longitude2, latitude2) > Double.parseDouble(radius);
}
}
2.判断一个坐标是否在一个多边形区域内
这里用到JAVA的一个类GeneralPath(由直线和二次和三次(B?zier)曲线构成的几何路径。 它可以包含多个子路径)使用这个类,结合传入的各顶点参数,画一个几何图形,并通过它自身的contains方法,判断该点是否在这个几何图形内。
package com.test.java.util;
import org.apache.commons.lang3.StringUtils;
import java.awt.geom.GeneralPath;
import java.awt.geom.Point2D;
import java.util.ArrayList;
import java.util.List;
/**
* 计算距离
*/
public class PositionUtil {
/**
* 判断坐标点是否在多边形区域内
*
* @param pointLon 要判断的点的经度
* @param pointLat 要判断的点的纬度
* @param lon 区域各顶点的经度数组
* @param lat 区域各顶点的纬度数组
* @return true:范围内; false:范围外
*/
public static boolean isInPolygon(double pointLon, double pointLat, double[] lon, double[] lat) {
// 将要判断的横纵坐标组成一个点
Point2D.Double point = new Point2D.Double(pointLon, pointLat);
// 将区域各顶点的横纵坐标放到一个点集合里面
List pointList = new ArrayList<>();
double polygonPointToX;
double polygonPointToY;
for (int i = 0; i < lon.length; i++) {
polygonPointToX = lon[i];
polygonPointToY = lat[i];
Point2D.Double polygonPoint = new Point2D.Double(polygonPointToX, polygonPointToY);
pointList.add(polygonPoint);
}
return check(point, pointList);
}
/**
* 坐标点是否在多边形内
*
* @param point 要判断的点的横纵坐标
* @param polygon 组成的顶点坐标集合
*/
private static boolean check(Point2D.Double point, List polygon) {
GeneralPath generalPath = new GeneralPath();
Point2D.Double first = polygon.get(0);
// 通过移动到指定坐标(以双精度指定),将一个点添加到路径中
generalPath.moveTo(first.x, first.y);
polygon.remove(0);
for (Point2D.Double d : polygon) {
// 通过绘制一条从当前坐标到新指定坐标(以双精度指定)的直线,将一个点添加到路径中。
generalPath.lineTo(d.x, d.y);
}
// 将几何多边形封闭
generalPath.lineTo(first.x, first.y);
generalPath.closePath();
// 测试指定的 Point2D 是否在 Shape 的边界内。
return generalPath.contains(point);
}
}
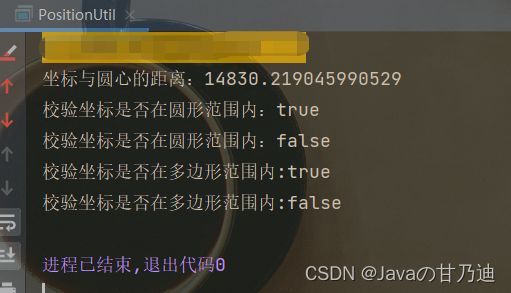
3.结果
public static void main(String[] args) {
double distance1 = PositionUtil.getDistance1(longitude1, latitude1, longitude2, latitude2);
System.out.println("坐标与圆心的距离:" + distance1);
String radius1 = "10000";
boolean inCircle1 = PositionUtil.isInCircle(longitude1, latitude1, longitude2, latitude2, radius1);
System.out.println("校验坐标是否在圆形范围内:" + inCircle1);
String radius = "15000";
boolean inCircle2 = PositionUtil.isInCircle(longitude1, latitude1, longitude2, latitude2, radius);
System.out.println("校验坐标是否在圆形范围内:" + inCircle2);
double pointLon = 117.274984;
double pointLat = 31.790718;
// 坐标在多边形范围内的参数:
double[] lon = {117.272559, 117.276224, 117.278649, 117.273924};
double[] lat = {31.791247, 31.792812, 31.78982, 31.788539};
// 坐标在多边形范围外的参数:
double[] lon1 = {117.291001, 117.299705, 117.298035, 117.291216};
double[] lat1 = {31.806576, 31.806814, 31.802319, 31.802196};
boolean a = PositionUtil.isInPolygon(pointLon, pointLat, lon, lat);
boolean b = PositionUtil.isInPolygon(pointLon, pointLat, lon1, lat1);
System.out.println("校验坐标是否在多边形范围内:" + a);
System.out.println("校验坐标是否在多边形范围内:" + b);
}
总结
这样的计算方式得到的距离并非是真实的距离,可以说是逻辑距离(直线距离),但其距离也已经很准确。不过毕竟是通过逻辑计算得到的距离,若要求高准确性的距离信息的话,还是借助第三方的地图api接口获取比较合适。
如果这篇文章对您有所帮助,或者有所启发的话,求一键三连:点赞、评论、收藏➕关注,您的支持是我坚持写作最大的动力。