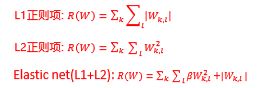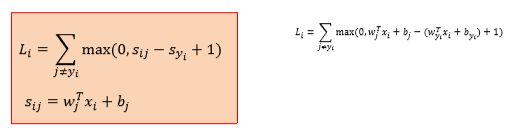计算机视觉系列一(前言/图像分类/线性分类器)-北京邮电大学-鲁鹏
目录
-
- 计算机视觉的目标
- 图像中包含哪些信息?
- 计算机视觉的研究进展
- 1、图像分类
-
- 1.1 什么是图像分类任务,它有哪些应用场合
- 1.2 图像分类任务有哪些难点?
- 1.3 基于规则的方法是否可行?
- 1.4 什么是数据驱动的图像分类范式
- 1.5 常用的分类任务的评价指标是什么?
- 2、线性分类器
-
- 2.1 准备数据
- 2.2关于分类模型
- 2.3损失函数
-
- 问题思考:
- 2.4 优化算法
- 2.5 数据集的划分
- 2.6 数据预处理
- 3、答案
- 4、作业
计算机视觉的目标
图像中包含哪些信息?
语义信息;三维场景的结构信息
计算机视觉的研究进展
1、动画产业
2、三维建模
3、摄影
4、虹膜识别
5、无人驾驶
6、人机交互
1、图像分类
图像分类任务,是视觉任务的各个基础,例如目标检测,图像分割,图像描述,图像生成。以上都是鲁老师这门课程要讲的东西。
对于视觉识别任务而言,目前最为有效的工具就是 卷积神经网络。
深度学习三要素:数据->算法->算力
1.1 什么是图像分类任务,它有哪些应用场合
图像分类任务是计算机视觉中的核心任务,其目标是根据图像信息中所反映的不同特征,把不同类别的图像进行区分。
1.2 图像分类任务有哪些难点?
1、视角
2、光照
3、尺度
4、遮挡
5、形变
6、背景杂波
7、类内扰动
8、运动模糊(一个像素记录位置的多个信息)
9、类别繁多
1.3 基于规则的方法是否可行?
什么是基于规则的方法?
通过硬编码的方式识别猫或其他类,硬编码单纯的靠人总结规律,但是世上千千万,这些工作是真的很费时费力。
1.4 什么是数据驱动的图像分类范式
之后引入了机器学习,深度学习这类数据驱动的分类范式。
ps:范式是符合某一种级别的关系模式的集合。
该类方法的三个步骤:
1、数据集构建
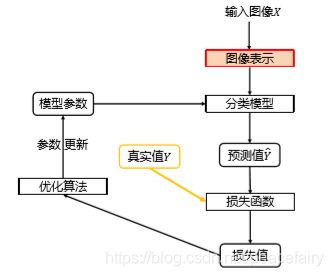
2、分类器设计与学习
3、分类器决策
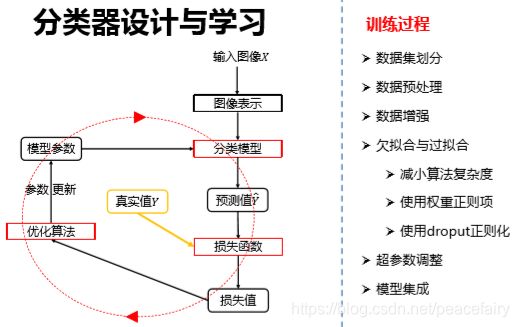
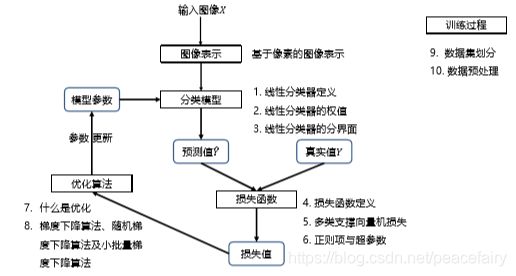
分类器的设计与学习
其中全局特征表示(GIST)->表示特征的提取依赖整张图片的信息,加入对象被遮挡了,就不行。
局部特征表示,从图像中抽出100个/n个有典型意义的区块,用这些区块来表示图像。
1.5 常用的分类任务的评价指标是什么?
正确率(accuracy) = 分对的样本数/全部样本数
错误率(error rate)= 1-正确率
top1正确率和top5正确率 要知道分别是什么意思。
2、线性分类器
2.1 准备数据
图像的表示,利用机器学习,不需要人为的去进行硬编码,可以让机器自己去学习。所以这里采用的就是基于像素的图像表示。
图像的类型:
1、binary,二进制图像,非0即1
2、灰度图像(0,255)单通道
3、彩色图像(h,w,3)三通道,我们常用的RGB图像
ps:大多数分类算法都要求输入向量
所以我们输入到分类算法中的也是矩阵转换成向量。
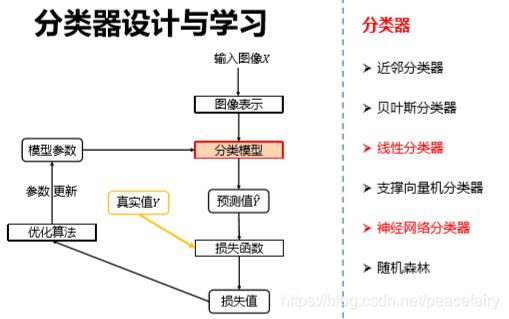
2.2关于分类模型
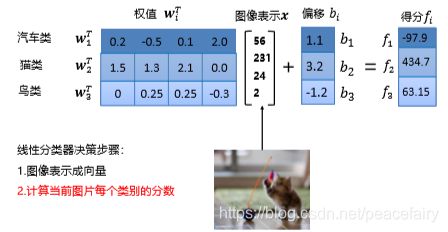
提问1: 在CIFAR10数据集分类任务的分类器,w,x,b的维度是多少?
答案在文章最后,请思考后翻看。
如何理解权值向量w,我们可以把w看成一个特征模板。输入图像与评估模型 的匹配程度越高,分类器输出的分数就越高。
分类就是找分类的边界,每个数据距离分类边界越远,分类分的就越好。
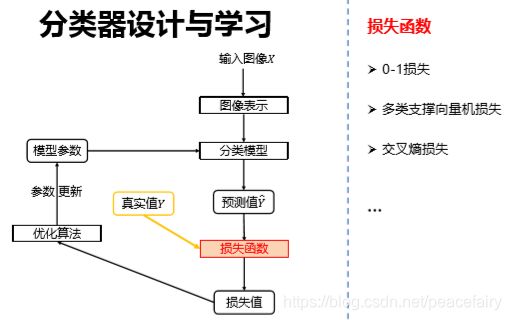
2.3损失函数
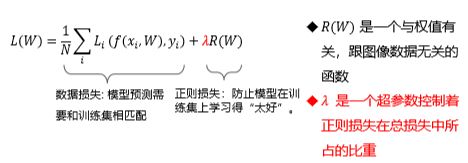
关于损失函数:如何评判分类器对当前样本的效果好坏。损失函数搭建了模型性能与模型参数之间的桥梁,指导模型参数优化。
损失函数是一个函数,用于度量给定分类器的预测值和真实值的不一致程度,其输出通常是一个非负实值。
其输出的非负实值可以作为反馈信号来对分类器的参数进行调整,以降低当前示例对应的损失值,提升分类器的分类效果。
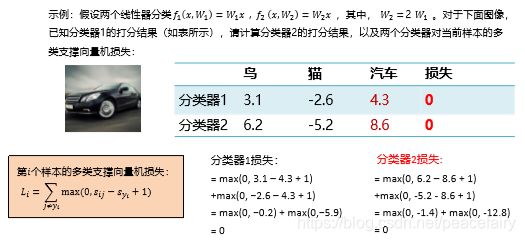
线性分类器,采用了多类支持向量机损失
公式:

横轴表示Syj,纵轴表示损失
问题思考:
让我们思考,假设存在一个W使损失函数L=0,这个W是唯一的吗? 不唯一。
这时我们引入了正则项。
λ = 0 优化结果仅与数据损失相关
λ = 无穷,优化结果与数据损失无关,仅考虑权重损失,此时系统最优解为W=0,因为我们要让损失函数变小,就要让正则损失变小,只有让λ这个极大值乘上0(极小的数)
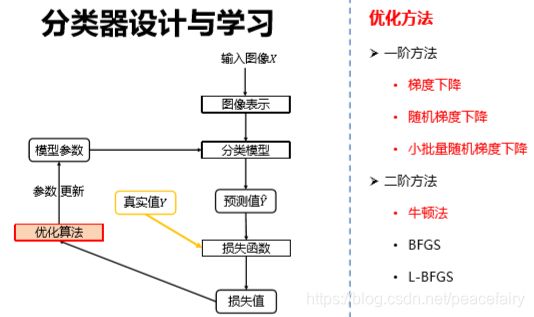
2.4 优化算法
优化就是根据损失给出的反馈对模型的参数进行修改。
参数优化是机器学习的核心步骤之一,它利用损失函数的输出值作为反馈信号来调增分类器的参数,以提升分类器对训练样本的预测性能。
优化算法常见的有:梯度下降算法,随机梯度下降算法,小批量梯度下降算法
ps:这三种优化算法的区别是什么?
梯度下降算法,告诉我们往哪儿走(负梯度方向),走多远(学习率超参数)
知道怎么办了,那么梯度如何求解?(梯度计算)
1、数值法,根据导数的定义进行求导
2、解析法:牛顿莱布尼兹 求导公式那些
那么数值法就可以用来验证解析法的正确与否。
2.5 数据集的划分
训练集用于给定的超参数时的分类器参数的学
验证集用于选择超参数
测试集评估泛化能力
如果数据很少,那么可能验证集包含的样本就太少,从而无法在统计上代表数据。
所以当数据量太少时,我们可以采用k折交叉验证或者带有打乱数据的重复K折验证。
设定好超参数,进行每折损失的计算,之后计算平均值即可代表我们的训练效果。
2.6 数据预处理
深度学习中的数据预处理方式:原始数据->去均值后的数据->归一化后的数据
机器学习常见的数据预处理方式:原始数据->去相关后的数据->白化后的数据
3、答案
提问1:有10各类别,则w(10,3072)x(3072) b (10,1),总结,每个类别都有一组w,b
问题抢答部分的答案:
1、根据损失函数,最大值为无穷,最小值为0
2、初始化w,b,假设w,b都取极小值0,那么损失L会是1
3、损失函数Li会增大1,带入公式进行求解可得,但是作用和原本没有差别,是等价的。
4、用求和代替平均,等价于原损失函数。
5、损失大的值越大,小的越小,加入了权重的思想,与原损失函数不等价。
三种优化算法的区别在于,每次更新所采取的的数据不一样,分别取全部数据,单个数据和m个数据。

随机梯度下降算法中,单个样本的训练可能会带来很多噪声,不是每次迭代都向着整体最优化方向。
4、作业
import numpy as np
def svm_loss_naive(W, X, y, reg):
'''
Inputs:
- W: A numpy array of shape (D, C) containing weights.
- X: A numpy array of shape (N, D) containing a minibatch of data.
- y: A numpy array of shape (N,) containing training labels; y[i] = c means
that X[i] has label c, where 0 <= c < C.
- reg: (float) regularization strength
Returns a tuple of:
- loss as single float
- gradient with respect to weights W; an array of same shape as W
'''
dW = np.zeros(W.shape) # initialize the gradient as zero
# compute the loss and the gradient
num_classes = W.shape[1]
num_train = X.shape[0]
loss = 0.0
for i in range(num_train):
scores = X[i].dot(W)
correct_class_score = scores[y[i]]
for j in range(num_classes):
if j == y[i]:
continue
margin = scores[j] - correct_class_score + 1 # note delta = 1
if margin > 0: # 也就是只有1(xiWj - xiWyi +1>0)的时候才进行loss和gradient的计算
loss += margin
dW[:, y[i]] += -X[i, :]
dW[:, j] += X[i, :]
# 上面两行代码这样理解,每张图片输入,就是i循环一次,对应的j循环了num_class次,就是把dW矩阵的每一列都遍历到了,(也就是每张图对应一个dW,i循环完了,就是将num_train个dW矩阵叠加了一遍),这里dW[:,y[i]]+= -X[i,:]在每一次i循环都执行,就是第y[i]列是其他列的和,其他列只循环了一次。
# if margin > 0: 表示有错误的评分出现,这个时候才会产生损失值,所以这里才会有loss的计算
# Right now the loss is a sum over all training examples, but we want it
# to be an average instead so we divide by num_train.
loss /= num_train
dW = dW / num_train
# Add regularization to the loss.
loss += 0.5 * reg * np.sum(W * W)
dW = dW + reg * W
return loss, dW
def svm_loss_vectorized(W, X, y, reg):
loss = 0.0
dW = np.zeros(W.shape) # initialize the gradient as zero
num_classes = W.shape[1]
num_train = X.shape[0]
scores = X.dot(W)
# 根据已知的y,找出本应该得分最高的分类得分,存放入一个矩阵,这个矩阵大小【1*N】
score_correct = scores[np.arange(num_train), y]
# 必须这样才能把矩阵变为[N*1],不能用转置,python中转置操作对以为矩阵不起作用(有点坑)
score_correct = np.reshape(score_correct, (num_train, 1))
# 矩阵化实现(xiW)j−(xyiW)j+Δ
margin_matrix = scores - score_correct + 1
# 因为loss公式中指明j=y[i]的列不参与计算,因为这一列是本应该分类正确的,其他列都是和这一列作比较。
margin_matrix[np.arange(num_train), y] = 0
margin_matrix[margin_matrix <= 0] = 0
# 计算所有loss的和
loss = np.sum(margin_matrix)
loss /= num_train
loss = loss + 0.5 * reg * np.sum(W * W)
# 这一步是对用梯度公式中 1(xiWj - xiWyi +1>0)) 这一项
margin_matrix[margin_matrix > 0] = 1
# 将所有非正确分类,且这个非正确分类的评分要大于正确的评分,做个求和
row_sum = np.sum(margin_matrix, axis=1)
margin_matrix[np.arange(num_train), y] = -row_sum
# 上面两句代码对应for循环中的dW[:,y[i]]+= -X[i,:]这一句
dW = np.dot(X.T, margin_matrix) / num_train + reg * W
# 然后根据矩阵的对应关系进行计算,就是维度关系
return loss, dW