python量化交易笔记---14.随机变量

随机变量用大写字母来表示，如$X$，其具体的观测值用小写字母来表示，如$x$。我们希望通过观测到的结果，来推断出随机变量的真实分布。根据随机变量的取值，分为离散随机变量和连续随机变量，在量化交易中，绝大多数数据都是连续随机变量。

1.概率与概率分布

1.1.离散型随机变量

假设离散型随机变量$X$，其所有取值的集合为$\{a_k\},k=1,2,3,...$，我们定义$X$的概率质量函数为：

$$f_X(a_k)=P\{X=a_k\},k=1,2,3,...$$

累积概率分布函数定义为：

$$F_X(a)=P\{X\le a\}=\sum _{i:a_i\le a}{f}_X(a_i)$$

我们假设随机变量$X$可以取的值为$\{1,2,3,4,5\}$，对应的概率为：$\{0.1,0.1,0.3,0.3,0.2\}$，根据此分布我们生成1000个点，打印出每个数值出现的概率和直方图，代码如下所示：

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

def startup():
    ''' 数据位置分析 '''
    num = 1000
    data = np.random.choice([1, 2, 3, 4, 5], size=num, replace=True, p=[0.1, 0.1, 0.3, 0.3, 0.2])
    xs = pd.Series(data)
    print(xs.value_counts() / num)
    plt.hist(xs)
    plt.show()
    
    
if '__main__' == __name__:
    startup()

codes/c14c001.py

运行结果为：

images/c14f001.png


images/c14f002.png

1.2.连续型随机变量

连续型随机变量取某个具体值的概率为0，即：$P_X(X=a_k)=0$。

累积分布函数定义：

$$F_X(a)=P_X\{X\le a\}={\int }_{-\infty }^a{f}_X(x)dx$$

概率密度函数定义：

$$f_X(x)=\frac{d{F}_X(x)}{dx}$$

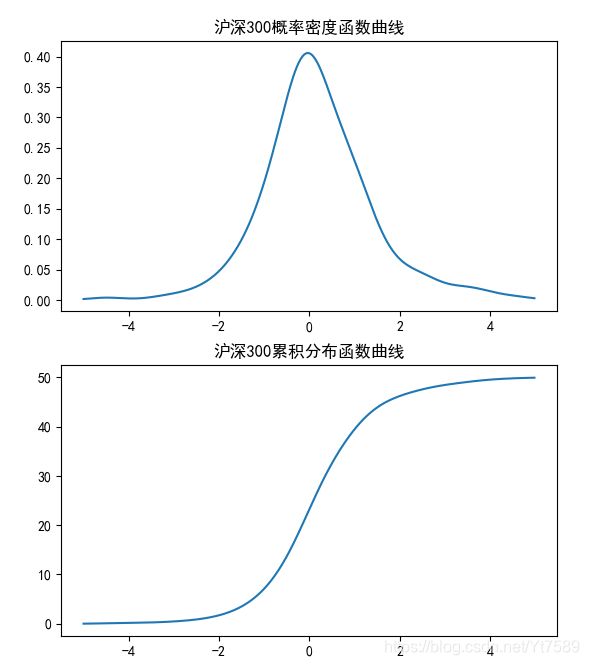
下面我们以2014年沪深300指数日收益率为例，绘制出其概率密度函数和累积分布函数的曲线，数据格式为：

images/c14f003.png

代码如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

def startup():
    data = pd.read_csv('../datas/return300.csv')
    f_x = stats.kde.gaussian_kde(data.iloc[:, 1])
    bins = np.arange(-5, 5, 0.02)
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.subplot(211)
    plt.title('沪深300概率密度函数曲线')
    plt.plot(bins, f_x(bins))
    plt.subplot(212)
    plt.title('沪深300累积分布函数曲线')
    plt.plot(bins, f_x(bins).cumsum())
    plt.show()    
    
if '__main__' == __name__:
    startup()

codes/c14c002.py

运行结果如下所示：

images/c14f004.png

2.期望与方差

2.1.离散随机变量

期望定义为：

$$E(X)=\sum _k{a}_k{f}_X(a_k)=\sum _k{a}_{k}P\{X=a_k\}$$

方差定义为：

$$Var(X)=E[X-E(X){]}^2=\sum _k[a_k-E(X){]}^{2}P\{X=a_k\}$$

光讲概念比较抽象，下面以伯努利分布为例。假设随机变量$X$服从伯努利分布，只能取值0或者1，其概率质量函数定义为：

$$f_X(x)=P\{X=x\}=\{\begin{array}{l}p,x=1\\ 1-p,x=0\end{array}$$

其希望值为：

$$E(X)=\sum _k{a}_{k}P\{X=a_k\}=1\cdot P\{X=1\}+0\cdot P\{X=0\}=1\cdot p+0\cdot (1-p)=p$$

方差为：

$$\begin{gathered} Var(X)=\sum _k[a_k-E(X){]}^{2}P\{X=a_k\}=(1-p{)}^{2}P\{X=1\}+(0-p{)}^{2}P\{X=0\} \\ =(1-p{)}^{2}p+p^2(1-p)=(1-p)p \end{gathered}$$

2.2.连续随机变量

期望定义：

$$E(X)={\int }_{-\infty }^{\infty }x{f}_X(x)dx$$

方差定义为：

$$Var(X)={\int }_{-\infty }^{\infty }[x-E(X){]}^2{f}_X(x)dx$$

3.二项分布

我们把伯努利变量多次观察值的过程称之为伯努利过程。假设随机变量$Y_i$代表第$i$次观察时$Y$取值为1或0的值，我们进行n次试验，每次实验中$Y_i$为1的概率为p，将$Y_i$为1的次数用随机变量$X\sim b(n,p)$表示：

$$X=\sum _{i=1}^n{Y}_i,X\in 0,1,2,...,n$$

3.1.性质

3.1.1.概率密度函数

$$\begin{gathered} f_X(k)=P\{X=k\}=C_n^k\cdot p^k\cdot (1-p{)}^{n-k} \\ {C}_n^k=\frac{n!}{k!\cdot (n-k)!} \end{gathered}$$

表示在n次试验中，有$k$次$Y_i$值为1的概率。

3.1.2.期望

$$E(X)=np$$

3.1.3.方差

$$Var(x)=np(1-p)$$

3.2.Python程序实现

程序如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

def startup():
    n = 100
    p = 0.5
    count = 20
    datas = np.random.binomial(n, p, count)
    print(datas)
    k = 20
    f_X = stats.binom.pmf(k, n, p)
    print('概率质量函数（20次正面概率）：{0}'.format(f_X))
    F_X = stats.binom.pmf(np.arange(0, 21, 1), n, p).sum()
    print('累积分布函数（小于等于20次正面概率）1：{0}'.format(F_X))
    F_X2 = stats.binom.cdf(k, n, p)
    print('累积分布函数（小于等于20次正面概率）2：{0}'.format(F_X2))
    
if '__main__' == __name__:
    startup()

codes/c14c003.py

运行结果如下所示：

images/c14f005.png

3.3.金融应用

在金融分析领域，如果我们设定收益率为正时为1，否则为0，就可以将其视为二项分布。我们还以沪深300在2014年的收益率为例，交易日为245天，相当于做了245次试验，我们可以求出收益率为正（即为1）的概率，我们就可以预测接下来10天收益率为正的概率，程序如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

def startup():
    data = pd.read_csv('../datas/return300.csv')
    ror = data.iloc[:, 1]
    p = len(ror[ror>0]) / len(ror)
    print('p={0}'.format(p))
    n = 10
    k = 6
    print('10天中6天上涨概率：{0}'.format(stats.binom.pmf(k, n, p)))
    
if '__main__' == __name__:
    startup()

codes/c14c004.py

运行结果为：

images/c14f006.png

4.正态分布

4.1.正态分布定义

对于连续型随机变量，正态分布又叫高斯分布，是自然界中广泛存在的一种分布，在金融和社会科学领域，也有很多应用场景。随机变量$X$服从希望为$\mu$和方差为${\sigma }^2$的正态分布表示为：$X\sim N(\mu ,{\sigma }^2),X\in (-\infty ,\infty )$。

概率密度函数定义：

$$f_X(x)=\frac{1}{\sqrt{2\pi \sigma }}{e}^{-\frac{(x-\mu {)}^2}{2{\sigma }^2}}$$

下面程序画出三个正态分布的曲线：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

def gaussian(mu, sigma, x):
    sigma2 = sigma ** 2
    return 1/np.sqrt(2*np.pi*sigma)*np.exp(-(x-mu)**2 / (2*sigma2))

def startup():
    x = np.linspace(-5, 7, 1000)
    # mu=0, sigma=1
    mu = 0
    sigma = 1
    y1 = gaussian(mu, sigma, x)
    plt.plot(x, y1)
    # mu=0, sigma = 2
    mu = 0
    sigma = 2
    y2 = gaussian(mu, sigma, x)
    plt.plot(x, y2)
    # mu = 1, sigma = 5
    mu = 2
    sigma = 3
    y3 = gaussian(mu, sigma, x)
    plt.plot(x, y3)
    plt.show()
    
if '__main__' == __name__:
    startup()

codes/c14/c005.py

运行结果为：

images/c14f007.png

4.2.正态分布规一化

可以将任意的正态分布$X\sim N(\mu ,{\sigma }^2)$转化为标准正态分布$Z\sim N(0,1)$，其统计性质不变：

$$Z=\frac{x-\mu }{\sigma }$$

4.3.正态分布金融上的应用

还以沪深300指数2014年日收益率数据库例，假设我们想要估计在其后的一天（2015-01-05）亏损在95%的情况下不会超过多少？假设我们认为沪深300指数2014年日收益率符合正态分布，我们可以先求出正态分布的参数：均值、方差，然后这个值，代码如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

def startup():
    data = pd.read_csv('../datas/return300.csv')
    ror = data.iloc[:, 1]
    mu = ror.mean()
    print('均值：{0}'.format(mu))
    sigma = ror.var()
    stdval = ror.std()
    print('方差：{0}; 标准差：{1}'.format(sigma, stdval))
    loss = stats.norm.ppf((1-0.95), mu, stdval)
    print('95%的情况下亏损不会高于：{0}%'.format(-loss))
    
if '__main__' == __name__:
    startup()

codes/c14c006.py

运行结果为：

images/c14f008.png

5.变量的关系

在金融分析中，我们通常需要考察股票对、营收与收益率等之间的关系，我们就需要研究变量间的关系。

5.1.联合概率分布

5.1.1.定义

对于随机变量$X$和$Y$，其所有可能取值集合分别为$\{x_i\}$和$\{y_j\}$，其中$i,j=1,2,3,...$的值，则$X$和$Y$的联合概率质量函数定义为：

$$f_{X,Y}(x_i,y_j)=P\{X=x_i且Y=y_j\},i,j=1,2,3,...$$

随机变量$X$和$Y$的联合累积分布函数定义为：

$$F_{X,Y}(x,y)=P\{X\le x且Y\le y\}$$

5.1.2.离散型

$$\begin{gathered} F_{X,Y}(x,y)=\sum _{i:x_i\le x}\sum _{j:y_j\le y}P\{X=x_i且Y=y_j\} \\ =\sum _{i:x_i\le x}\sum _{j:y_j\le y}{f}_{X,Y}(x_i,y_j) \end{gathered}$$

边际概率函数定义为：

$$f_X(x_i)=\sum _j{f}_{X,Y}(x_i,y_j)$$

期望值定义为：

$$\begin{gathered} E(X)=\sum _i\sum _j{x}_i\cdot f_{X,Y}(x_i,y_j)=\sum _i{x}_i\sum _j{f}_{X,Y}(x_i,y_j) \\ =\sum _i{x}_i\cdot f_X(x_i) \end{gathered}$$

同理可以求出E(Y)，这里就不再给出证明了。

5.1.3.连续型

累积分布函数定义为：

$$F_{X,Y}(a,b)={\int }_{-\infty }^{\infty }{\int }_{-\infty }^{\infty }{f}_{X,Y}(x,y)dxdy$$

概率密度函数比较复杂，这里就不再讲述了。

5.2.变量的独立性

随机变量$X$和$Y$的联合累积分布函数满足：

$$F_{X,Y}(x,y)=F_X(x)\cdot F_Y(y)$$

则称随机变量$X$和$Y$相互独立，同时具有：

$$f_{X,Y}(x,y)=f_X(x)\cdot f_y(y)$$

对于离散型随机变量有：

$$P\{X=x且Y=y\}=P\{X=x\}\cdot P\{Y=y\}$$

5.3.变量的相关性

随机变量$X$和随机变量$Y$的协方差定义为：

$$Cov(X,Y)=E\left[\right(X-E(X)\left)\right(Y-E(Y)\left)\right]$$

协方差具有如下性质：

$$\begin{gathered} Cov(X,Y)=Cov(Y,X) \\ Cov(aX,bY)=abCov(X,Y)a,b为常数 \\ Cov(X_1+X_2,Y)=Cov(X_1,Y)+Cov(X_2,Y) \end{gathered}$$

协方差大小不具有直接可比性，因此我们定义相关系数：

$${\rho }_{X,Y}=\frac{Cov(X,Y)}{{\sigma }_X{\sigma }_Y}$$

其取值为$[-1,1]$。$\rho$为正数时值越大，则表明$X$增大$Y$增大的越明显；$\rho$为负数时值越小，则表明$X$增大时$Y$减小越明显。

5.4.相关性分析举例

我们以上证综指和深证综指日收益率数据为例，来分这两个指数的相关性。程序如下所示：

import numpy as np
import pandas as pd
from scipy import stats
import matplotlib.pyplot as plt

def startup():
    data = pd.read_table('../datas/TRD_Index.txt')
    shIndex = data[data.Indexcd==1] # 上证综指编号为1
    szIndex = data[data.Indexcd==399106] # 深证综指编号为399106
    # 计算相关系数
    szIndex.index = shIndex.index
    rho = szIndex.Retindex.corr(shIndex.Retindex)
    # 绘制相关性图形
    plt.rcParams['font.sans-serif'] = ['SimHei']
    plt.rcParams['axes.unicode_minus'] = False
    plt.title('上证综指与深证综指相关性(rho={0})'.format(rho))
    plt.xlabel('上证综指')
    plt.ylabel('深证综指')
    plt.scatter(shIndex.Retindex, szIndex.Retindex)
    plt.show()
    
if '__main__' == __name__:
    startup()

codes/c14c007.py

运行结果为：

images/c14f009.png

由上图可以看出，深证综指和上证综指从图形上看几乎形成一个直线，而相关系数为0.9，证明这二者之间存在非常强的正相关性。