字符串系列1 Rabin-Karp, 有限自动机, KMP, 扩展 KMP

阅读目录：

这篇博客总结了几种常见的字符串匹配的处理方法，并使用 python 实现，参考了算法导论以及其他博客。

算法导论的四种字符串匹配算法

字符串匹配问题的形式化定义如下：假设文本是一个长度为 $n$ 的数组 $T\left[1..n\right]$，而模式是一个长度为 $m$ 的数组 $P\left[1..m\right]$，其中 $m<n$，进一步假设 $P$ 和 $T$ 的元素都是来自一个有限字母集 $\Sigma$ 的字符。例如，$\Sigma =\left\{0,1\right\}$ 或者 $\Sigma =\left\{a,b,..,z\right\}$。字符数组 $P$ 和 $T$ 通常称为字符串。为了使符号简洁，我们把模式 $P\left[1..m\right]$ 的由 $k$ 个字符组成的前缀 $P\left[1..k\right]$ 记作 $P_k$，把文本 $T$ 中由 $k$ 个字符组成的前缀 $T\left[1..k\right]$ 记作 $P_k$。
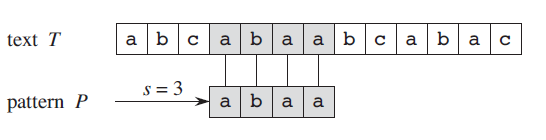
如图所示，如果 $0⩽s⩽n-m$，并且 $T\left[s+1..s+m\right]=P\left[1..m\right]$（即如果 $T\left[s+j\right]=P\left[j\right]$, 其中 $1⩽i⩽m$），那么称模式 $P$ 在文本 $T$ 中出现，且偏移为 $s$（或者等价地，模式 $P$ 在文本 $T$ 中出现的位置是以 $s+1$ 开始的）。如果 $P$ 在 $T$ 中以偏移 $s$ 出现，那么称 $s$ 是有效偏移；否则，称它为无效偏移。字符串匹配问题就是找到所有的有效偏移，使得在该有效偏移下，所给的模式 $P$ 出现在给定的文本 $T$ 中。下面的讲解中，字符串下标都是从1开始，而在所有 Python 程序中，下标从0开始，分析时间复杂度时，$m$ 指的是模式串的长度，$n$ 指的是文本串的长度。

1. 朴素字符串匹配算法

朴素字符串匹配算法相当于寻找文本 $T$ 的所有子串，然后和模式 $P$ 进行比较，比较简单不再赘述，Python 代码如下：

import os
def native_string_matcher(txt, pat):
    t_len = len(txt)
    p_len = len(pat)
    for s in range(t_len - p_len):
        if pat[0:p_len] == txt[s:s + p_len]:
            print "Pattern occurs with shift " + str(s) + os.linesep

最坏情况下，外层循环共运行 $n-m+1$ 次，每次比较两字符串是否相等需要比较 $m$ 个字符，因此总的时间复杂度为 $\text{O}\left(\left(n-m+1\right)m\right)$ ，空间复杂度为 $0$。

2. Rabin-Karp算法

算法的核心思想是将字符串映射到一个数字，然后比较字符串对应的数字或者对应数字的模是否相等，如果相等则继续进一步判断确认正确性，如果不相等，则可以判断字符串不匹配。最坏情况下的时间复杂度依然为 $\text{O}\left(\left(n-m+1\right)m\right)$，但是基于一些假设，在平均情况情况下，它的运行时间还是比较好的（期望运行时间为$\text{O}\left(n\right)$）。
先用简单的例子来理解：
假设字符集全是由0到9的数字组成，即 $\Sigma =\left\{0,1,..,9\right\}$。对于一个长度为 $m$ 的模式串 $P\left[1..m\right]$，用 $p$ 表示该字符串对应的含有 $m$ 个数字的整数（比如将“123”看作数字123），用 $t_s$ 来表示长度为 $m$ 的子字符串 $T\left[s+1..s+m\right]$ 对应的十进制数，当且仅当 $p=t_s$ 时有 $P\left[1..m\right]=T\left[s+1..s+m\right]$。
把长度为 $m$ 的字符串转换为对应的整数，时间复杂度为 $O(m)$。通过下面的公式进行转换即可：
$$p=P\left[m\right]+\text{10(}P\left[m-1\right]+10\left(P\left[m-2\right]+\dots .+\left(10\left(P\left[2\right]\right)+P\left[1\right]\right)\dots \right)$$
因此我们分别可以在 $O(m)$ 时间内计算出 $p$ 和 $t_0$，并在 $O(n-m)$ 时间内利用下面公式计算出剩余的 $t_1，t_2，..，t_{n-m}$：
$$t_{s+1}=10\left(t_s-10^{m-1}T\left[s+1\right]\right)+T\left[s+m+1\right]$$
简单来说，就是去掉高位 $T[s+1]$ 并加上低位 $T[s+m+1]$，例如，如果 $m=5$，$t_s=31415$，$T[s+5+1]=2$，我们希望去掉高位数字3，并加入低位数字2，则：
$$t_s=10\left(31415-10000\cdot 3\right)+2$$
这就是 Rabin-Karp 算法巧妙的地方，对于剩下 $n-m$ 个数字，将前一次匹配的信息 $t_s$ 应用到后一次匹配 $t_{s+1}$ 中。朴素的字符串匹配算法慢的原因就是它太健忘了，前一次匹配的信息其实可以有部分可以应用到后一次匹配中的，而朴素的字符串匹配算法只是简单的把这个信息扔掉，从头再来，因此，浪费了时间。好好的利用这些信息，自然可以提高运行速度。
将上述思想应用到一般的字符串匹配：首先需要解决的问题就是如果 $p$ 和 $t_s$ 值过大怎么办？如果 $P$ 包含 $m$ 个字符，那么关于在 $p$（$m$数位长）上的每次算数运算需要“常数”时间这一假设就不合理了（过大会导致数值溢出，当两个过大的数值比较大小或进行运算的时候时，CPU需要多个运算周期来进行）。解决方法就是选取一个合适的模 $q$ 来计算 $p$ 和 $t_s$ 的模。还有需要解决的问题就是，如果字符串含非数字怎么办？如果处理的文本是小写字符 $\left\{a,b..z\right\}$， 其实本质是一样的，只要把十进制的数值 $\left\{0..9\right\}$ 换成26进制的数字 $\left\{0,1,..25\right\}$，上面公式中的10换成26即可。因此在一般情况下，采用 $d$ 进制的字母表 $\left\{0,1,..d-1\right\}$ 时，选取一个 $q$ 值，使得 $dq$ 在一个计算机字长内，然后调整上面的递归式，使其能够对模 $q$ 有效，式子变为：
$$t_{s+1}=\left(d\left(t_s-T\left[s+1\right]h\right)+T\left[s+m+1\right]\right)modq$$
其中，$h$ 是和 $d^{m-1}$ 模 $q$ 相同的数（$h\equiv d^{m-1}\left(modq\right)$），但是基于模q得到的结果并不完美：$t\equiv p\left(modq\right)$ 并不能说明 $t=p$，需要被进一步检测，看 $s$ 是真的有效还是仅仅是一个伪命中点。这项额外的测试可以通过检测条件 $T\left[s+1..s+m\right]=P\left[1..m\right]$ 来完成，如果 $q$ 足够大，那么这个伪命中点可以尽量少出现，从而使额外测试的代价降低。这也是为什么在最坏情况下的时间复杂度和朴素算法一样，因为最坏情况下，需要对每一个有效偏移进行进一步检验，每次检验花费的时间为 $O(m)$。但是另一方面，如果 $t̸=p\left(modq\right)$，那么可以断定 $t̸=p$，从而确定偏移 $s$是无效的。示例如下：

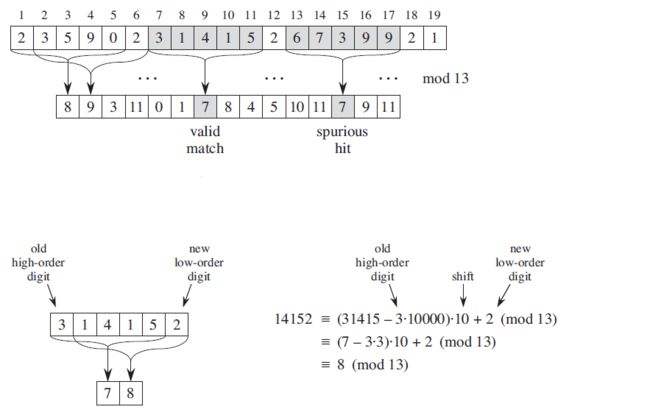
Python 代码如下，这里选取 $d=128$ 设为 ASCII 表的长度，并将每个字符直接转化成 ASCII 表对应的数值（Python 的 API 为 ord() ），理论上 d 的选取只要大于等于字符串中出现的不同字母的数量即可：

import os
def rabin_karp_matcher(txt, pat, q):
    p_len = len(pat)
    t_len = len(txt)
    if p_len == 0 or t_len == 0:
        print "Empty string"
    p = 0 # hash value for pattern
    t = 0 # hash value for txt
    d = 128 # number of characters
    h = 1
    # pow(d, p_len - 1) % q
    for i in range(p_len - 1):
        h = (d * h) % q
    for i in range(p_len):
        p = (d * p + ord(pat[i])) % q
        t = (d * t + ord(txt[i])) % q
    for i in range(t_len - p_len):
        if p == t and txt[i:i + p_len] == pat:
            print "Pattern occurs with shift " + str(i) + os.linesep
        if i < t_len - p_len:
            t = (d * (t - ord(txt[i]) * h) + ord(txt[i + p_len])) % q
        # t may have negative values
        if t < 0:
            t += q

3. 利用有限自动机进行字符串匹配

有限自动机是楼主在编译原理的课程中学习的，有限自动机最典型的应用就是词法分析器，应用到字符串匹配也不是很难，而且个人觉得理解了有限自动机，再去理解 KMP 算法就小菜一碟了。

确定有限自动机简介

有限自动机严格说分为确定有限自动机和非确定有限自动机，这里用到的是确定有限自动机，因此下面的有限自动机都指的都是确定有限自动机，对非确定有限自动机不一定成立。有限自动机的形式化定义如下，一个有限自动机 $M$ 是一个五元组 $\left(Q,q_0,A,\Sigma ,\delta \right)$，即任何一个有限状态机都必须有五元组的五个部分构成，其中：

• $Q$ 是状态的集合。
• $q_0\in Q$ 是初始状态，一个有限自动机只有一个初始状态。
• $A\subseteq Q$ 是终止状态集。
• $\Sigma$ 是有限输入字符集合。有限状态机一次只能接收一个确定的输入，接受之后只能处于一个确定的状态。
• $\delta$ 是一个从 $Q\times \Sigma$ 到 $Q$ 的函数，称为 $M$ 的转移函数。

我们先根据上述定义来定义一个有限自动机，定义 $Q=\left\{\text{0,}1\right\}$ ，$q_0=0$，$A=\{1\}$，$\Sigma =\left\{a,b\right\}$，$\delta$ 由下图中 (a) 来表示，包括 $\delta \left(\text{0,}a\right)=1$。一个有限自动机可以使用一个有向图形象地来表示，这个有限自动机就可以使用图 (b) 来表示，其中每个圆圈都代表一个状态，这里使用涂黑的方式标记终止状态（只要能标记初始状态和终止状态，标记随意，比如楼主上学的时候就在初始节状态对应的节点上方额外添加一个 + 号，而在所有的终止状态上方添加一个 - 号），有向图的每一条边都有起点、终点、边上字符、以及方向，它其实就代表了状态转移函数对应的表格中的一项，比如从状态0到状态1那一项就对应着 $\delta \left(\text{0,}a\right)=1$，所有有向边上的字符合起来自然就是有限状态机的字符集。

有限自动机可以表示一类字符串的集合。就以上图为例，由于任何自动机都是由初始状态开始，因此我们就从0开始，此时假设我们遇到字符 a，则由图或者 $\delta \left(\text{0,}a\right)=1$ 可以看出此时状态机由状态0转为状态1，由于状态1是终止状态，因此此时可以立即终止，这种情况下，有限自动机就代表由单个字符构成的字符串 “a”，即自动机接受 “a”，但是注意到状态1还有出边，说明状态1可以继续接受字符，假设此时遇到字符 b，则自动机从状态1又转到状态0，状态0继续接受字符串，此时若停止，因为0不是终止状态，则此时的字符串，即 “ab” 就不是自动机可以表示的了，即自动机拒绝 “ab”。因此这个有限自动机接受的是以奇数个 a 结尾的字符串，更具体地，一个字符串 $x$ 被接受，当且仅当 $x=yz$，其中 $y=\epsilon$（y为空串）或者 $y$ 以一个 $b$ 结尾，并且 $z=a^k$，这里 $k$ 为奇数。其实有限自动机能代表的远非这些，如果上述有限自动机的字符集 $a,b$ 分别代表数字和26个字母，则它表示的就是奇数个数字结尾的字符串。更多有限自动机的知识大家还是阅读龙书（编译原理）吧。

利用有限自动机进行字符串匹配

我们先定义一些符号，文本串 $T$ 以 $T[i]$ 结尾的子串设为 $T_i$，比如下图中 $T_4=bacb$，$P$ 以 $P[j]$ 结尾的子串设为 $P_j$，即P的前缀 $P_j$，比如$P_5=ababa$。利用有限自动机进行字符串匹配，最主要的思想就是充分利用已经匹配的字符串的信息，即寻找一个子串，它既是模式串 $P$ 的前缀又是文本串 $T$ 的某子串的后缀。这里比较绕，下面来解释为什么要寻找这种子串，字符串匹配的过程分为两种情况：

1. 匹配的情况下，继续比较文本串和模式串已经匹配部分的下一个字符
2. 不匹配的话，模式串继续向右滑动，偏移加 k（朴素模式中 k 恒为1）。

我们只关注匹配部分以及匹配部分的下一个字符串，比如下图中，假设现在已经匹配5个字符，文本串的下一个字符（即 $T[10]$）如果是 $c$ 的话，那么已经匹配的字符串数量就会加1，即此时已经匹配6个字符，然后继续进行匹配即进入情况1。但是如果下一个字符如果是 $a$ 即不匹配的话，朴素字符串匹配算法会向右滑动一个单位，然后去比较 $T_{10}$ 的后5个字符串（即 $T_{10}$ 的后缀 $babaa$，注意这也是 $P_5+a=ababaa$ 的后缀）和 $P_5$ （即 $P_5+a=ababaa$ 的前缀）是否相等，相等则此时匹配5个字符然后进入上述情况1，不相等继续滑动，此时去比较 $T_{10}$ 的后4个字符串即 $T_{10}$ 的后缀和 $P_4$ 的否相等，如果不相等就这样一直继续下去，当滑动6个单位，即 $T_{10}$ 的后缀中没有一个是 $P$ 的前缀。下一个字符是 $b$ 的情况和 $a$ 一样。

从这个过程中可以看出，在模式串的前缀 $P_j$ 已经和文本串 $T_i$ 的后缀匹配 $j$ 个字符的情况下，即 $P_j$ 所有后缀也是 $T_i$ 所有后缀，我们只要能提前计算出 $P_{j+1}$ 的前缀和 $P_j+x$ 的后缀的匹配情况，当文本串中的下一个字符是 $x$ 的时候，我们就可以直接得到 $P_{j+1}$ 的前缀和 $T_j+x$ 的后缀匹配情况（已经提前计算出 $P_{j+1}$ 的前缀和 $P_j+x$ 的后缀的匹配情况，并且 $P_j+x$ 的后缀就是 $T_j+x$ 的后缀）。由于 $x$ 可能是字符串的字母表的任意字符，因此需要遍历字母表中所有字符。其实所有的 $P_j+x$ 的情况其实就相当于所有可能遇到的文本串的情况。
如果我们将计算出 $P_j+x$ 的前缀和后缀的最大匹配字符数作为状态，$P_j$ 可以看做 $P_{j-1}+P[j]$ ，即 $P_j$ 计算出的状态就是 $j$，每个 $x$ 作为有限状态机图有向边上的字母， $P_j+x$ 的结果作为状态转移的结果，那么计算出所有的 $0⩽j⩽\left|P\right|+1$ 就可以构造出一个有限状态机。
下面以算法导论的例子来实际说明如何计算状态转移函数：
假设模式串和文本串都是由 $\Sigma =\left\{a,b,c\right\}$ 中字母构成的字符串，$P=ababaca$ ，那么我们来计算它的下图所示的状态转移函数，这里 $0⩽j⩽7$ ：

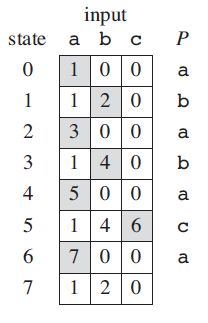
$j=0$ 时，$P_0=\epsilon$，此时状态机也处于初始状态0，由于模式串首字母为 $a$，也就是说只有遇到 $a$ 的时候才会发生状态转变，遇到 $a$ 时转为状态1。
$j=1$ 时，$P_1=a$，我们来计算状态转移函数值：

1. $P_{1}a=aa,P_2=ab$，此时既是 $P_{1}a$ 后缀又是 $P_2$ 前缀的子串的长度为 1，即 $a$。
2. $P_{1}b=ab,P_2=ab$，此时既是 $P_{1}b$ 后缀又是 $P_2$ 前缀的子串的长度为 2，即 $ab$。
3. $P_{1}c=ac,P_2=ab$，此时既是 $P_{1}c$ 后缀又是 $P_2$ 前缀的子串的长度为 0。

$j=2$ 时，$P_2=ab$，我们来计算状态转移函数值：

1. $P_{2}a=aba,P_3=aba$，此时既是 $P_{2}a$ 后缀又是 $P_3$ 前缀的子串的长度为 3，即 $aba$。
2. $P_{2}b=abb,P_3=aba$，此时既是 $P_{2}b$ 后缀又是 $P_3$ 前缀的子串的长度为 0。
3. $P_{2}c=abc,P_3=aba$，此时既是 $P_{2}c$ 后缀又是 $P_3$ 前缀的子串的长度为 0。

……
最终构造的有限状态机如下图所示：

Python 代码如下，最坏情况下，$compute\_transition\_function$ 的时间复杂度为 $O\left(m^3\left|\Sigma \right|\right)\left(m=len\left(pat\right),\left|\Sigma \right|=len\left(sigma\right)\right)$，因为最外层循环最多循环 $m$ 次，下两层最多循环 $len(sigma)$，$m$ 次，最后的比较字符串最多比较 $m$ 个字符，$finite\_automaton\_matcher$ 的时间复杂度为 $O\left(n\right)$：

import os
def compute_transition_function(pat, sigma=None):
    """Compute transition.
 
    Compute transition of the finite automaton.
 
    Args:
        pat: A pattern string.
        sigma:A set of all the characters that appear in pattern and text,default None,and will be set set(pat).
 
    Returns:
        A dict that represents the state transition table,
        the key is the (state,character).
        For example: {(0, a): 1, (0,b): 0, etc.}
 
    """
    p_len = len(pat)
    if sigma is None:
        sigma = set(pat)
    delta = {}
    for q in range(p_len + 1):
        for x in sigma:
            k = q + 1
            while k > 0:
                px = pat[:q] + x
                if pat[:k] == px[len(px) - k:]:
                    break
                k -= 1
            delta[q, x] = k
    return delta
 
 
def finite_automaton_matcher(txt, pat, sigma=None):
    """String matching.
 
    String-matching with finite automaton.
 
    Args:
        txt: A text string.
        pat: A pattern string.
        sigma:A set of all the characters that appear in pattern and text, default None, and will be set set(pat).
 
    """
    delta = compute_transition_function(pat, sigma)
    t_len = len(txt)
    p_len = len(pat)
    q = 0
    for i in range(t_len):
        q = delta[q, txt[i]]
        if q == p_len:
            print "Pattern occurs with shift " + str(i - q + 1) + os.linesep

4. KMP算法

其实 KMP 算法和有限自动机算法的核心思想是一样的，只不过 KMP 少了构造有限自动机的时间。
对于 KMP 算法我们需要做的就是对于模式串 $P$ 的每一个前缀，确定最长的既是真前缀又是真后缀的子串的长度（一个字符串的真前缀不包括它本身，而前缀包含）。为什么要寻找这种子串呢？

字符串匹配可以看做模式串一直向右滑动，由上图 (a) 可以看出，当文本串字符 $T[i+1]$ 和模式串字符 $P[i+1]$ 不发生匹配的时候，即 $T\left[i+1\right]̸=P\left[i+1\right]$，$P$ 需要向右继续滑动至少一个单位，若滑动一个单位时，此时 $P$ 的已经匹配的部分（即$P$ 的前缀 $P_i$，为了便于说明，假设下标从1开始）的最后一个字符即 $P[i]$ 将和文本串的已经匹配的部分的下一个字符即 $T[i+1]$ 比较，由于我们只知道 $T\left[i+1\right]̸=P\left[i+1\right]$ ，即使知道 $P[i]$ 和 $P[i+1]$ 的关系，我们也无法判断 $P[i]$ 和 $T[i+1]$ 的关系，之后字符的关系就更无法判断了，因此我们可以利用的就是已经匹配的字符串的信息。拿图 (a) 说话，滑动1个单位时，已经匹配的部分的前4个字符会和已经匹配部分的后4个字符比较(即 $P_5$ 的前缀 $P_4$ 和 $P_5$ 的后缀比较)，滑动2个单位，$P_5$ 的前3个字符和后3个字符比较，这样一只滑动下去，最多滑动5个单位即跳过了所有已经匹配的部分。如果我们能预先确定 $P_5$ 的最长的既是前缀又是后缀的子串（即构成 $P_5$ 真后缀的 $P$ 的最长前缀）的长度 $q$（这里 $q=3$），我们就可以在文本串和模式串已经匹配5个字符，第6个字符不匹配的时候直接将模式串滑动 $5-q$ 个单位，然后去比较 $P[q+1]$ 和 $T[i+1]$ 是否相等，然后继续重复上面的步骤。 比如上图中，在 a 和 c，即 $P[6]$ 和 $T[10]$ 不发生匹配的时候，已经匹配5个字符，而 $P_5$ 的最长的既是前缀又是后缀的子串长度是3，因此我们滑动2个单位，然后继续比较 $P[4]$ 和 $T[10]$ 是否相等，这里不相等，此时已经匹配的字符数是3并且 $P_3$ 的最长的既是前缀又是后缀的子串长度是1，因此我们继续滑动2个单位，比较 $P[2]$ 和 $T[10]$ 是否相等，这里依然不相等，再滑动一个单位，这就跳过了所有已经匹配的部分，需要从头开始慢慢比较了。我们先来看一下这个过程的伪代码，这个过程很清晰，我就不再说了：

由上面的分析可知，KMP 算法的关键就是：若已知一个模式 $P[1..m]$ ，确定构成 $P_k$ 真后缀的 $P$ 的最长前缀的长度 $q$，其中，若下标从1开始的话， $1⩽k⩽m$，从0开始就是 $0⩽k⩽m-1$。即模式 $P$ 的前缀函数是函数 $\pi :\left\{\text{1,2,..,}m\right\}\to \left\{\text{0,1..,}m-1\right\}$ 满足
$$\pi \left[q\right]=\max \left\{k:k<q\text{ 且 }{P}_k\text{是}{P}_q\text{的后缀}\right\}$$
下面还是以 $P=ababaca$ 为例来说明具体怎么算前缀函数。

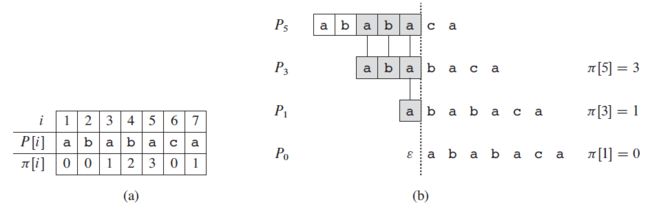
(1) i = 1，对于模式串的首字符，我们统一为 $\pi \left[1\right]=0$；
(2) i = 2，前面的字符串为 ab，其最长相同真前后缀长度为 0，即 $\pi \left[2\right]=0$；
(3) i = 3，前面的字符串为 aba，其最长相同真前后缀长度为 1，即 $\pi \left[3\right]=1$；
(4) i = 4，前面的字符串为 abab，其最长相同真前后缀长度为 2，即 $\pi \left[4\right]=2$；
……

上述过程的伪代码如下：

你会发现 $KMP-MATCHER$ 和 $COMPUTE-PREFIX-FUNCTION$ 很相似，原因很简单，他们都是一个字符串针对模式 $P$ 的匹配：$KMP-MATCHER$ 是文本 $T$ 针对模式 $P$ 的匹配，$COMPUTE-PREFIX-FUNCTION$ 是模式 $P$ 针对自己的匹配。
上述两个伪代码的下标都是从1开始的，具体实现的时候，我们得自己选择从0开始开始还是从1开始，如下图所示，有的人将下标从0开始的的前缀函数的每个值都减1，相应的程序也会发生细微变化，具体区别参考这个：KMP 算法（2）：其细微之处。

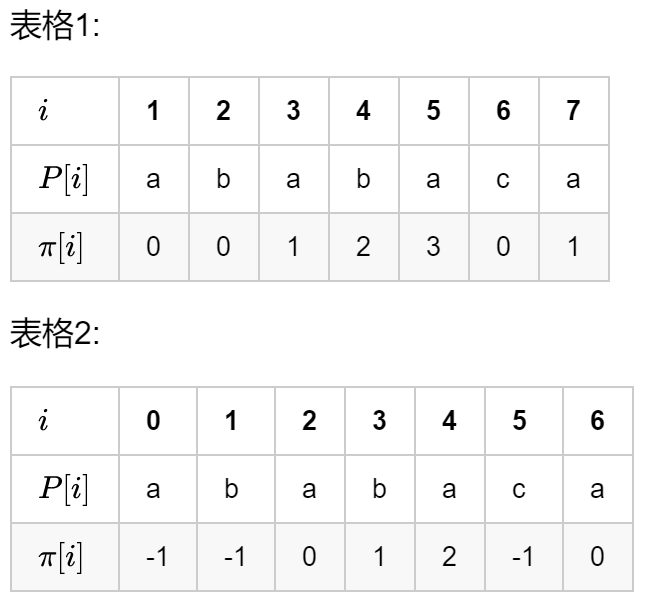
但是我们只要稍微改动伪代码，也可以实现下面图片所示的效果，下面的 Python 程序就是下标从0开始的下面的表格4的实现，其实无论是上面的做法，还是我这种做法，都是完全等价的，只要你理解了 KMP 算法，你就会发现这几种写法其实没有什么区别，这里我的建议是，写逻辑时先随便确定一下边界然后写好了所有的逻辑之后自己亲自加断点去看看边界是啥，这样既能加深理解，又可以调边界条件：

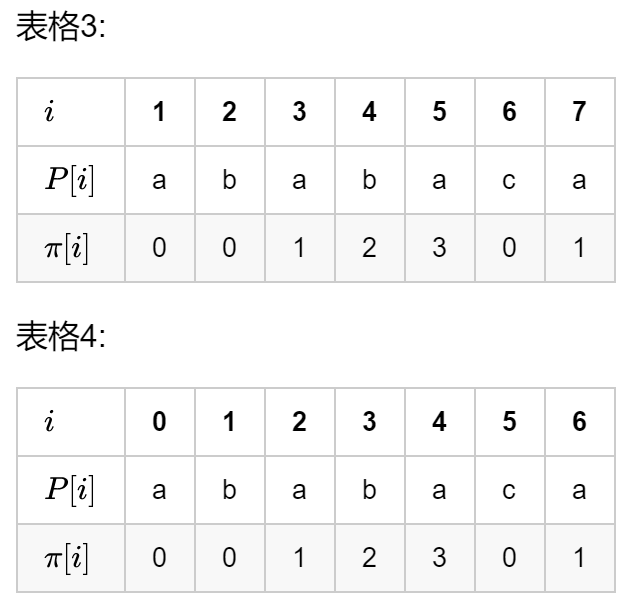
Python函数如下（已将 Python 函数改写成 C++ 通过 POJ 3416 Oulipo，两个 C++ 程序这里放在最后的附录吧） 。最坏情况下，$kmp\_matcher$ 的时间复杂度为 $O\left(n\right)$，$compute\_prefix\_function$ 的时间复杂度为 $O\left(m\right)$。

import os
def kmp_matcher(txt, pat):
    t_len = len(txt)
    p_len = len(pat)
    pi = compute_prefix_function(pat)
    q = 0
    for i in range(t_len):
        while q > 0 and pat[q] != txt[i]:
            q = pi[q - 1]
        if pat[q] == txt[i]:
            q += 1
        if q == p_len:
            print "Pattern occurs with shift " + str(i - p_len + 1) + os.linesep
            q = pi[q - 1]
 
 
def compute_prefix_function(pat):
    p_len = len(pat)
    pi = [0] * p_len
    k = 0
    for q in range(1, p_len):
        while k > 0 and pat[k] != pat[q]:
            k = pi[k - 1]
        if pat[k] == pat[q]:
            k += 1
        pi[q] = k
    return pi

其他字符串相关算法

这里我找了几篇已经写得很好的博客，我就不再继续写了，或者说等博主有了更深一步的理解之后再继续写这两种算法。

KMP 优化

上面讲解 KMP 的时候说过，当文本串字符 $T[i+1]$ 和模式串字符 $P[i+1]$ 匹配失败的时候，通过预先计算的前缀函数，我们可以确定向前移动几个单位，然后再进行比较，如果不相等则继续滑动，直到滑过所有已经匹配部分，再重新从 $P[0]$ 开始比较。因此你会发现，如果能在匹配失败情况下，能一下确定最终的滑动位置，则匹配速度会加快，这就是 KMP 继续优化的方向。拿 KMP 部分的第一个图来说，当 $P[6]$ 和 $T[10]$ 不发生匹配的时候，我们没有必要先滑动2个单位。再滑动2个单位，最后再滑动1个单位，我们可以直接滑动5个单位。
这篇博客 KMP算法 最后的部分有实现这种算法，这里不再说了。

拓展 KMP 算法

扩展 KMP 算法

附录

表格3实现（POJ 3416 Oulipo 通过）：

#include
#include
 
int n, m;
char txt[1000010], pat[10010];
int pi[11111];
 
void getPi() {
    pi[1] = 0;
    int q, k = 0;
    for (q = 2; q <= m; q++) {
        while (k > 0 && pat[k + 1] != pat[q]) k = pi[k];
        if (pat[k + 1] == pat[q]) k += 1;
        pi[q] = k;
    }
}
 
int kmp() {
    int i, q = 0, cnt = 0;
    for (i = 1; i <= n; i++) {
        while (q > 0 && pat[q + 1] != txt[i]) q = pi[q];
        if (pat[q + 1] == txt[i]) q += 1;
        if (q == m) {
            cnt++;
            q = pi[q];
        }
    }
    return cnt;
}
 
int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        scanf("%s%s", pat + 1, txt + 1);
        m = strlen(pat + 1);
        n = strlen(txt + 1);
        getPi();
        printf("%d\n", kmp());
    }
}

表格4实现（POJ 3416 Oulipo 通过）：

#include
#include
 
int n, m;
char txt[1000010], pat[10010];
int pi[11111];
 
void getPi() {
    pi[0] = 0;
    int q, k = 0;
    for (q = 1; q < m; q++) {
        while (k > 0 && pat[k] != pat[q]) k = pi[k-1];
        if (pat[k] == pat[q]) k += 1;
        pi[q] = k;
    }
}
 
int kmp() {
    int i, q = 0, cnt = 0;
    for (i = 0; i < n; i++) {
        while (q > 0 && pat[q] != txt[i]) q = pi[q -1];
        if (pat[q] == txt[i]) q += 1;
        if (q == m) {
            cnt++;
            q = pi[q - 1];
        }
    }
    return cnt;
}
 
int main() {
    int t;
    scanf("%d", &t);
    while (t--) {
        scanf("%s%s", pat, txt);
        m = strlen(pat);
        n = strlen(txt);
        getPi();
        printf("%d\n", kmp());
    }
}