13年12月CCF计算机软件能力认证

4、有趣的数

时间限制： 1.0s
内存限制： 256.0MB
问题描述：
问题描述
　　我们把一个数称为有趣的，当且仅当：
　　1. 它的数字只包含0, 1, 2, 3，且这四个数字都出现过至少一次。
　　2. 所有的0都出现在所有的1之前，而所有的2都出现在所有的3之前。
　　3. 最高位数字不为0。
　　因此，符合我们定义的最小的有趣的数是2013。除此以外，4位的有趣的数还有两个：2031和2301。
　　请计算恰好有n位的有趣的数的个数。由于答案可能非常大，只需要输出答案除以1000000007的余数。
输入格式
　　输入只有一行，包括恰好一个正整数n (4 ≤ n ≤ 1000)。
输出格式
　　输出只有一行，包括恰好n 位的整数中有趣的数的个数除以1000000007的余数。
样例输入
4
样例输出
3

思路分析：
解法一（状态机）：
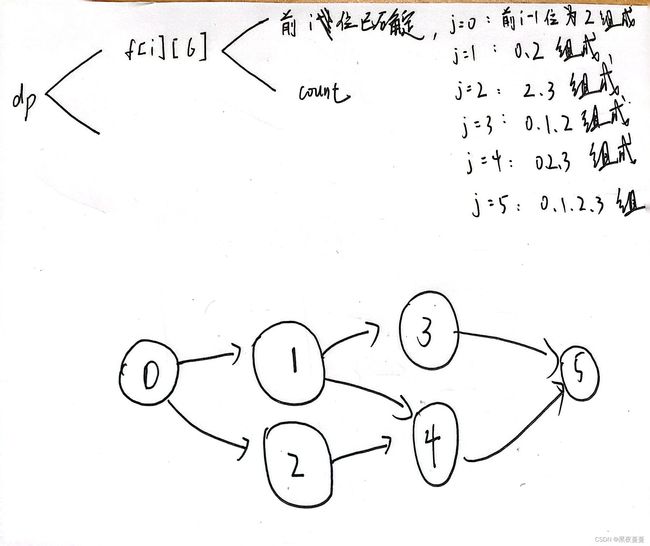
由题目可知，0在1前，2在3前，可知第一位必定为2，则前n-1位全为2为状态一；
第二位可能的值为0或3，则前n-1位由2,0组成为状态二，前n-1位由2、3组成为状态三（01已确定）；
若前n-1位由0、2组成，则第n位1或3，则前n-1位由012组成为状态四，前n-1位由023组成为状态五；
前n-1位0123全部用过为状态六

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define int long long

using namespace std;

typedef pair PII;

const int N=1010,mod=1000000007;

int n;
int f[N][10];

void solve()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        f[i][0]=1;//前i位全为2只有一种
        f[i][1]=(2*f[i-1][1]+f[i-1][0])%mod;//前i-1为全为2，第i位为0；前i-1位为02，第i位可能为0/2
        f[i][2]=(  f[i-1][2]+f[i-1][0])%mod;//前i-1为全为2，第i位为3；前i-1位为23，第i位必定为3
        f[i][3]=(2*f[i-1][3]+f[i-1][1])%mod;//前i-1为全为02，第i位为1；前i-1位为012，第i位可能为1/2
        f[i][4]=(2*f[i-1][4]+f[i-1][1]+f[i-1][2])%mod;
        f[i][5]=(2*f[i-1][5]+f[i-1][3]+f[i-1][4])%mod;
    }
    
    cout<>tt;
    while(tt--) solve();
}

解法二（枚举思路+组合数）：
由题目可知，可以分成01和23两个组合，设01所占的位数为k位，则2<=k<=n-2,则23占n-k位；假设先放01，由于第一位必须为2，则01一共有C[n-1][k]种，由于k-1位中0的个数不同，所以01也有k-1种放法。同理23有n-k-1种放法

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

#define int long long

using namespace std;

typedef pair PII;

const int N=1010,mod=1000000007;

int n;
int c[N][N];
int res=0;

void init()//初始化组合数
{
    for(int i=0;i<=1005;i++)
    {
        for(int j=0;j<=i;j++)
        {
            if(!j) c[i][j]=1;
            else
            {
                c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
            }
        }
    }
}
void solve()
{
    cin>>n;
    init();
    for(int i=2;i<=n-2;i++)
    {
        res=(res+(c[n-1][i]*(i-1)*(n-i-1))%mod)%mod;
    }
    cout<>tt;
    while(tt--) solve();
}

5、I’m stuck!

时间限制： 1.0s
内存限制： 256.0MB
问题描述：
问题描述
　　给定一个R行C列的地图，地图的每一个方格可能是’#‘, ‘+’, ‘-’, ‘|’, ‘.’, ‘S’, ‘T’七个字符中的一个，分别表示如下意思：
　　‘#’: 任何时候玩家都不能移动到此方格；
　　‘+’: 当玩家到达这一方格后，下一步可以向上下左右四个方向相邻的任意一个非’#‘方格移动一格；
　　‘-’: 当玩家到达这一方格后，下一步可以向左右两个方向相邻的一个非’#‘方格移动一格；
　　‘|’: 当玩家到达这一方格后，下一步可以向上下两个方向相邻的一个非’#‘方格移动一格；
　　‘.’: 当玩家到达这一方格后，下一步只能向下移动一格。如果下面相邻的方格为’#’，则玩家不能再移动；
　　‘S’: 玩家的初始位置，地图中只会有一个初始位置。玩家到达这一方格后，下一步可以向上下左右四个方向相邻的任意一个非’#‘方格移动一格；
　　‘T’: 玩家的目标位置，地图中只会有一个目标位置。玩家到达这一方格后，可以选择完成任务，也可以选择不完成任务继续移动。如果继续移动下一步可以向上下左右四个方向相邻的任意一个非’#‘方格移动一格。
　　此外，玩家不能移动出地图。
　　请找出满足下面两个性质的方格个数：
　　1. 玩家可以从初始位置移动到此方格；
　　2. 玩家不可以从此方格移动到目标位置。
输入格式
　　输入的第一行包括两个整数R 和C，分别表示地图的行和列数。(1 ≤ R, C ≤ 50)。
　　接下来的R行每行都包含C个字符。它们表示地图的格子。地图上恰好有一个’S’和一个’T’。
输出格式
　　如果玩家在初始位置就已经不能到达终点了，就输出“I’m stuck!”（不含双引号）。否则的话，输出满足性质的方格的个数。
样例输入
5 5
–±+
…|#.
…|##
S-±T
####.
样例输出
2
样例说明
　　如果把满足性质的方格在地图上用’X’标记出来的话，地图如下所示：
　　--±+
　　…|#X
　　…|##
　　S-±T
　　####X
思路分析：
先从终点跑一边BFS或者DFS找到可以到达终点的点
再从起点跑一边BFS或者DFS完成题目要求

#include 
#include 
#include 
#include 

using namespace std;

const int N = 55;

char g[N][N];
int n, m;
bool st1[N][N], st2[N][N];
int dx[4] = {-1, 0, 1, 0}, dy[4] = {0, 1, 0, -1};  // 上左下右

bool check(int x, int y, int i)  // 判断当前点x, y是否能够沿着指示i走
{
    if(g[x][y] == 'S' || g[x][y] == 'T' || g[x][y] == '+') return true;
    if(g[x][y] == '-' && (i == 1 || i == 3)) return true;  // 如果可以往左右走(括号顺序不能忘记)
    if(g[x][y] == '|' && (i == 0 || i == 2)) return true;  // 如果可以往上下走
    if(g[x][y] == '.' && i == 2) return true;  // 如果可以向下走

    return false;
}

void bfs1(int x, int y)
{
    st1[x][y] = true;

    for(int i = 0; i < 4; i ++ )
    {
        int tx = x + dx[i], ty = y + dy[i];
        if(tx <= 0 || tx > n || ty <= 0 || ty > m) continue;
        if(g[tx][ty] == '#') continue;
        if(check(x, y, i) && !st1[tx][ty])  // 如果当前点能够满足i的要求 并且下一个点没有被遍历过
        bfs1(tx, ty);
    }
}

void bfs2(int x, int y)
{
    st2[x][y] = true;

    for(int i = 0; i < 4; i ++ )
    {
        int tx = x + dx[i], ty = y + dy[i];
        if(tx <= 0 || tx > n || ty <= 0 || ty > m) continue;
        int k = i ^ 2;  // 由于是相反操作，从终点走往其他所有点，需要将i的要求变化，原本0 变 2, 1 变 3。而^2就可以满足这个式子  
        if(g[tx][ty] == '#') continue;
        if(check(tx, ty, k) && !st2[tx][ty])  // bfs1是从a -> b，bfs2是从b -> a，判断时的条件需要按照a的条件进行反向运算。
        bfs2(tx, ty);
    }
}

int main()
{
    cin >> n >> m;

    int s_x, s_y, e_x, e_y;

    for(int i = 1; i <= n; i ++ ) 
        for(int j = 1; j <= m; j ++ )
        {    
            cin >> g[i][j];
            if(g[i][j] == 'S') s_x = i, s_y = j;
            if(g[i][j] == 'T') e_x = i, e_y = j;
        }   

    bfs1(s_x, s_y);

    if(!st1[e_x][e_y])  // 如果从起点不能走到终点
    {
        cout << "I'm stuck!" << endl;
        return 0;
    }

    bfs2(e_x, e_y);

    int cnt = 0;
    for(int i = 1; i <= n; i ++ )
        for(int j = 1; j <= m; j ++ )
            if(st1[i][j] && !st2[i][j])  // 如果能够从起点走到当前点，但是终点不能走到当前点
                cnt ++ ;

    cout << cnt << endl;

    return 0;
}