Want595

【深度学习】实验13 使用Dropout抑制过拟合

文章目录

使用Dropout抑制过拟合
- 1. 环境准备
- 2. 导入数据集
- 3. 对所有数据的预测
- - 3.1 数据集
  - 3.2 构建神经网络
- 3.3 训练模型
- - 3.4 分析模型
- 4. 对未见过数据的预测
- - 4.1 划分数据集
  - 4.2 构建神经网络
  - 4.3 训练模型
  - 4.4 分析模型
- 5. 使用Dropout抑制过拟合
- - 5.1 构建神经网络
  - 5.2 训练模型
  - 5.3 分析模型
- 6. 正则化
- - 6.1 神经网络太过复杂容易过拟合
  - 6.2 太简单容易欠拟合
  - 6.3 选取适当的神经网络
附：系列文章

使用Dropout抑制过拟合

Dropout是一种常用的神经网络正则化方法，主要用于防止过拟合。在深度学习中，由于网络层数过多，参数数量庞大，模型容易过拟合，并且在测试时产生较大的泛化误差。Dropout方法借鉴了集成学习中的Bagging思想，通过随机的方式，将一部分神经元的输出设置为0，从而减少过拟合的可能。

Dropout方法最早由Hinton等人提出，其基本思想是在训练时，以一定的概率随机地将网络中某些神经元的输出置为0。这种随机的行为可以被看作是一种对网络进行了部分剪枝，从而增加了网络的容忍性，使网络更加健壮，同时也避免了网络中某些特定的神经元对整个网络的过度依赖。

Dropout方法的具体实现如下：在每次训练过程中，以一定的概率p随机选择一部分神经元并将其置为0，被选择的神经元不参与后续的训练和反向传播。在测试时，为了保持模型的稳定性和一致性，一般不会采取随机化的方式，而是将每个神经元的权重乘以概率p，这里的p是在训练时选择的那个概率。

Dropout方法不仅可用于全连接网络，也可用于卷积神经网络和循环神经网络中，以减少过拟合现象。并且，它的实现简单，仅需要在模型训练时对每个神经元以概率p随机地进行挑选和保留，所以Dropout方法得到了广泛的应用和推广。

总之，Dropout方法可以在一定程度上提高模型的准确性和泛化能力，对于防止过拟合有着较好的效果。但是需要注意的是，Dropout方法会导致训练过程中每个mini-batch的梯度都不同，所以在使用Dropout方法时需要调整学习率，以保证模型的收敛速度和效果。

1. 环境准备

# 导入库
import keras
from keras import layers
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

Using TensorFlow backend.

2. 导入数据集

# 导入数据集
data = pd.read_csv('./dataset/credit-a.csv', header=None)
data

	0	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
0	0	30.83	0.000	0	0	9	0	1.250	0	0	1	1	0	202	0.0	-1
1	1	58.67	4.460	0	0	8	1	3.040	0	0	6	1	0	43	560.0	-1
2	1	24.50	0.500	0	0	8	1	1.500	0	1	0	1	0	280	824.0	-1
3	0	27.83	1.540	0	0	9	0	3.750	0	0	5	0	0	100	3.0	-1
4	0	20.17	5.625	0	0	9	0	1.710	0	1	0	1	2	120	0.0	-1
5	0	32.08	4.000	0	0	6	0	2.500	0	1	0	0	0	360	0.0	-1
6	0	33.17	1.040	0	0	7	1	6.500	0	1	0	0	0	164	31285.0	-1
7	1	22.92	11.585	0	0	2	0	0.040	0	1	0	1	0	80	1349.0	-1
8	0	54.42	0.500	1	1	5	1	3.960	0	1	0	1	0	180	314.0	-1
9	0	42.50	4.915	1	1	9	0	3.165	0	1	0	0	0	52	1442.0	-1
10	0	22.08	0.830	0	0	0	1	2.165	1	1	0	0	0	128	0.0	-1
11	0	29.92	1.835	0	0	0	1	4.335	0	1	0	1	0	260	200.0	-1
12	1	38.25	6.000	0	0	5	0	1.000	0	1	0	0	0	0	0.0	-1
13	0	48.08	6.040	0	0	5	0	0.040	1	1	0	1	0	0	2690.0	-1
14	1	45.83	10.500	0	0	8	0	5.000	0	0	7	0	0	0	0.0	-1
15	0	36.67	4.415	1	1	5	0	0.250	0	0	10	0	0	320	0.0	-1
16	0	28.25	0.875	0	0	6	0	0.960	0	0	3	0	0	396	0.0	-1
17	1	23.25	5.875	0	0	8	0	3.170	0	0	10	1	0	120	245.0	-1
18	0	21.83	0.250	0	0	1	1	0.665	0	1	0	0	0	0	0.0	-1
19	1	19.17	8.585	0	0	2	1	0.750	0	0	7	1	0	96	0.0	-1
20	0	25.00	11.250	0	0	0	0	2.500	0	0	17	1	0	200	1208.0	-1
21	0	23.25	1.000	0	0	0	0	0.835	0	1	0	1	2	300	0.0	-1
22	1	47.75	8.000	0	0	0	0	7.875	0	0	6	0	0	0	1260.0	-1
23	1	27.42	14.500	0	0	10	1	3.085	0	0	1	1	0	120	11.0	-1
24	1	41.17	6.500	0	0	8	0	0.500	0	0	3	0	0	145	0.0	-1
25	1	15.83	0.585	0	0	0	1	1.500	0	0	2	1	0	100	0.0	-1
26	1	47.00	13.000	0	0	3	2	5.165	0	0	9	0	0	0	0.0	-1
27	0	56.58	18.500	0	0	1	2	15.000	0	0	17	0	0	0	0.0	-1
28	0	57.42	8.500	0	0	11	1	7.000	0	0	3	1	0	0	0.0	-1
29	0	42.08	1.040	0	0	9	0	5.000	0	0	6	0	0	500	10000.0	-1
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
623	1	28.58	3.750	0	0	0	0	0.250	1	0	1	0	0	40	154.0	1
624	0	22.25	9.000	0	0	12	0	0.085	1	1	0	1	0	0	0.0	1
625	0	29.83	3.500	0	0	0	0	0.165	1	1	0	1	0	216	0.0	1
626	1	23.50	1.500	0	0	9	0	0.875	1	1	0	0	0	160	0.0	1
627	0	32.08	4.000	1	1	2	0	1.500	1	1	0	0	0	120	0.0	1
628	0	31.08	1.500	1	1	9	0	0.040	1	1	0	1	2	160	0.0	1
629	0	31.83	0.040	1	1	6	0	0.040	1	1	0	1	0	0	0.0	1
630	1	21.75	11.750	0	0	0	0	0.250	1	1	0	0	0	180	0.0	1
631	1	17.92	0.540	0	0	0	0	1.750	1	0	1	0	0	80	5.0	1
632	0	30.33	0.500	0	0	1	1	0.085	1	1	0	0	2	252	0.0	1
633	0	51.83	2.040	1	1	13	7	1.500	1	1	0	1	0	120	1.0	1
634	0	47.17	5.835	0	0	9	0	5.500	1	1	0	1	0	465	150.0	1
635	0	25.83	12.835	0	0	2	0	0.500	1	1	0	1	0	0	2.0	1
636	1	50.25	0.835	0	0	12	0	0.500	1	1	0	0	0	240	117.0	1
637	1	37.33	2.500	0	0	3	1	0.210	1	1	0	1	0	260	246.0	1
638	1	41.58	1.040	0	0	12	0	0.665	1	1	0	1	0	240	237.0	1
639	1	30.58	10.665	0	0	8	1	0.085	1	0	12	0	0	129	3.0	1
640	0	19.42	7.250	0	0	6	0	0.040	1	0	1	1	0	100	1.0	1
641	1	17.92	10.210	0	0	13	7	0.000	1	1	0	1	0	0	50.0	1
642	1	20.08	1.250	0	0	0	0	0.000	1	1	0	1	0	0	0.0	1
643	0	19.50	0.290	0	0	5	0	0.290	1	1	0	1	0	280	364.0	1
644	0	27.83	1.000	1	1	1	1	3.000	1	1	0	1	0	176	537.0	1
645	0	17.08	3.290	0	0	3	0	0.335	1	1	0	0	0	140	2.0	1
646	0	36.42	0.750	1	1	1	0	0.585	1	1	0	1	0	240	3.0	1
647	0	40.58	3.290	0	0	6	0	3.500	1	1	0	0	2	400	0.0	1
648	0	21.08	10.085	1	1	11	1	1.250	1	1	0	1	0	260	0.0	1
649	1	22.67	0.750	0	0	0	0	2.000	1	0	2	0	0	200	394.0	1
650	1	25.25	13.500	1	1	13	7	2.000	1	0	1	0	0	200	1.0	1
651	0	17.92	0.205	0	0	12	0	0.040	1	1	0	1	0	280	750.0	1
652	0	35.00	3.375	0	0	0	1	8.290	1	1	0	0	0	0	0.0	1

653 rows × 16 columns

data.iloc[:, -1].unique()

array([-1,  1])

3. 对所有数据的预测

3.1 数据集

x = data.iloc[:, :-1].values
y = data.iloc[:, -1].replace(-1, 0).values.reshape(-1, 1)

x.shape, y.shape

((653, 15), (653, 1))

3.2 构建神经网络

model = keras.Sequential()
model.add(layers.Dense(128, input_dim=15, activation='relu'))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.summary()

Model: "sequential_1"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_1 (Dense)              (None, 128)               2048      
_________________________________________________________________
dense_2 (Dense)              (None, 128)               16512     
_________________________________________________________________
dense_3 (Dense)              (None, 128)               16512     
_________________________________________________________________
dense_4 (Dense)              (None, 1)                 129       
=================================================================
Total params: 35,201
Trainable params: 35,201
Non-trainable params: 0
_________________________________________________________________

model.compile(optimizer='adam',
              loss='binary_crossentropy',
              metrics=['acc']
)

WARNING:tensorflow:From /home/nlp/anaconda3/lib/python3.7/site-packages/tensorflow/python/ops/nn_impl.py:180: add_dispatch_support..wrapper (from tensorflow.python.ops.array_ops) is deprecated and will be removed in a future version.
Instructions for updating:
Use tf.where in 2.0, which has the same broadcast rule as np.where

3.3 训练模型

history = model.fit(x, y, epochs=1000)

WARNING:tensorflow:From /home/nlp/anaconda3/lib/python3.7/site-packages/keras/backend/tensorflow_backend.py:422: The name tf.global_variables is deprecated. Please use tf.compat.v1.global_variables instead.

Epoch 1/1000
653/653 [==============================] - 0s 434us/step - loss: 7.5273 - acc: 0.5988
Epoch 2/1000
653/653 [==============================] - 0s 92us/step - loss: 3.7401 - acc: 0.6187
Epoch 3/1000
653/653 [==============================] - 0s 75us/step - loss: 3.6464 - acc: 0.5712
Epoch 4/1000
653/653 [==============================] - 0s 56us/step - loss: 10.2291 - acc: 0.6631
Epoch 5/1000
653/653 [==============================] - 0s 63us/step - loss: 2.0400 - acc: 0.6233
Epoch 6/1000
653/653 [==============================] - 0s 120us/step - loss: 2.4279 - acc: 0.6217
Epoch 7/1000
653/653 [==============================] - 0s 105us/step - loss: 2.3289 - acc: 0.6325
Epoch 8/1000
653/653 [==============================] - 0s 159us/step - loss: 3.2521 - acc: 0.6294
Epoch 9/1000
653/653 [==============================] - 0s 89us/step - loss: 2.6005 - acc: 0.6294
Epoch 10/1000
653/653 [==============================] - 0s 118us/step - loss: 1.3997 - acc: 0.6738
……
Epoch 1000/1000
653/653 [==============================] - 0s 106us/step - loss: 0.2630 - acc: 0.9326

3.4 分析模型

history.history.keys()

dict_keys(['loss', 'acc'])

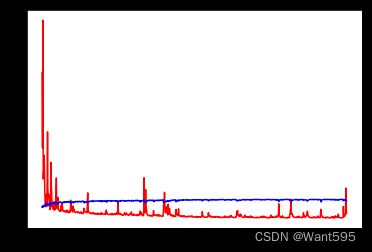
plt.plot(history.epoch, history.history.get('loss'), c='r')
plt.plot(history.epoch, history.history.get('acc'), c='b')

[]

4. 对未见过数据的预测

4.1 划分数据集

x_train = x[:int(len(x)*0.75)]
x_test = x[int(len(x)*0.75):]
y_train = y[:int(len(x)*0.75)]
y_test = y[int(len(x)*0.75):]

x_train.shape, x_test.shape, y_train.shape, y_test.shape

((489, 15), (164, 15), (489, 1), (164, 1))

4.2 构建神经网络

model = keras.Sequential()

model.add(layers.Dense(128, input_dim=15, activation='relu'))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

#admam:利用梯度的一阶矩估计和二阶矩估计动态调整每个参数的学习率.
model.compile(optimizer='adam',
              loss='binary_crossentropy',
              metrics=['acc']
)

4.3 训练模型

history = model.fit(x_train, y_train, epochs=1000, validation_data=(x_test, y_test))

Train on 489 samples, validate on 164 samples
Epoch 1/1000
489/489 [==============================] - 0s 487us/step - loss: 14.4564 - acc: 0.5951 - val_loss: 3.3778 - val_acc: 0.7256
Epoch 2/1000
489/489 [==============================] - 0s 110us/step - loss: 6.0909 - acc: 0.6012 - val_loss: 2.0924 - val_acc: 0.7195
Epoch 3/1000
489/489 [==============================] - 0s 195us/step - loss: 2.4527 - acc: 0.6074 - val_loss: 1.0763 - val_acc: 0.7378
Epoch 4/1000
489/489 [==============================] - 0s 183us/step - loss: 1.0751 - acc: 0.6585 - val_loss: 0.8990 - val_acc: 0.7134
Epoch 5/1000
489/489 [==============================] - 0s 155us/step - loss: 1.2669 - acc: 0.6503 - val_loss: 1.8094 - val_acc: 0.6585
Epoch 6/1000
489/489 [==============================] - 0s 202us/step - loss: 3.6742 - acc: 0.6892 - val_loss: 1.1836 - val_acc: 0.4573
Epoch 7/1000
489/489 [==============================] - 0s 166us/step - loss: 1.7544 - acc: 0.7301 - val_loss: 2.0060 - val_acc: 0.4573
Epoch 8/1000
489/489 [==============================] - 0s 185us/step - loss: 1.4768 - acc: 0.6605 - val_loss: 0.8917 - val_acc: 0.5427
Epoch 9/1000
489/489 [==============================] - 0s 163us/step - loss: 1.6829 - acc: 0.6667 - val_loss: 4.7695 - val_acc: 0.4573
Epoch 10/1000
489/489 [==============================] - 0s 157us/step - loss: 8.4323 - acc: 0.7239 - val_loss: 2.0879 - val_acc: 0.7439
……
Epoch 1000/1000
489/489 [==============================] - 0s 97us/step - loss: 0.0272 - acc: 0.9877 - val_loss: 2.2746 - val_acc: 0.8049

4.4 分析模型

history.history.keys()

dict_keys(['val_loss', 'val_acc', 'loss', 'acc'])

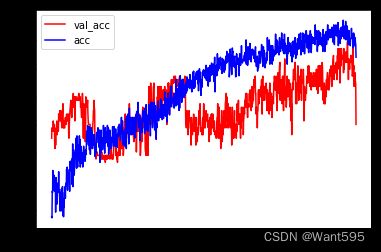
plt.plot(history.epoch, history.history.get('val_acc'), c='r', label='val_acc')
plt.plot(history.epoch, history.history.get('acc'), c='b', label='acc')
plt.legend()

model.evaluate(x_train, y_train)

489/489 [==============================] - 0s 37us/step
[0.021263938083038197, 0.9897750616073608]

model.evaluate(x_test, y_test)

164/164 [==============================] - 0s 46us/step
[2.274633582976715, 0.8048780560493469]

过拟合：在训练数据正确率非常高，在测试数据上比较低

5. 使用Dropout抑制过拟合

5.1 构建神经网络

model = keras.Sequential()
model.add(layers.Dense(128, input_dim=15, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(128, activation='relu'))
model.add(layers.Dropout(0.5))
model.add(layers.Dense(1, activation='sigmoid'))

model.summary()

Model: "sequential_3"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
dense_9 (Dense)              (None, 128)               2048      
_________________________________________________________________
dropout_1 (Dropout)          (None, 128)               0         
_________________________________________________________________
dense_10 (Dense)             (None, 128)               16512     
_________________________________________________________________
dropout_2 (Dropout)          (None, 128)               0         
_________________________________________________________________
dense_11 (Dense)             (None, 128)               16512     
_________________________________________________________________
dropout_3 (Dropout)          (None, 128)               0         
_________________________________________________________________
dense_12 (Dense)             (None, 1)                 129       
=================================================================
Total params: 35,201
Trainable params: 35,201
Non-trainable params: 0
________________________________________________________________

model.compile(optimizer='adam',
              loss='binary_crossentropy',
              metrics=['acc']
)

5.2 训练模型

history = model.fit(x_train, y_train, epochs=1000, validation_data=(x_test, y_test))

Train on 489 samples, validate on 164 samples
Epoch 1/1000
489/489 [==============================] - 1s 1ms/step - loss: 41.6885 - acc: 0.5378 - val_loss: 9.9666 - val_acc: 0.6768
Epoch 2/1000
489/489 [==============================] - 0s 298us/step - loss: 53.1358 - acc: 0.5358 - val_loss: 11.0265 - val_acc: 0.6951
Epoch 3/1000
489/489 [==============================] - 0s 173us/step - loss: 36.9899 - acc: 0.5828 - val_loss: 11.6578 - val_acc: 0.6890
Epoch 4/1000
489/489 [==============================] - 0s 177us/step - loss: 43.3404 - acc: 0.5808 - val_loss: 7.5652 - val_acc: 0.6890
Epoch 5/1000
489/489 [==============================] - 0s 197us/step - loss: 23.3085 - acc: 0.6196 - val_loss: 7.9913 - val_acc: 0.6890
Epoch 6/1000
489/489 [==============================] - 0s 254us/step - loss: 24.1833 - acc: 0.6155 - val_loss: 5.5747 - val_acc: 0.7073
Epoch 7/1000
489/489 [==============================] - 0s 229us/step - loss: 19.7051 - acc: 0.5890 - val_loss: 5.5711 - val_acc: 0.7012
Epoch 8/1000
489/489 [==============================] - 0s 180us/step - loss: 22.1131 - acc: 0.5849 - val_loss: 7.0290 - val_acc: 0.6890
Epoch 9/1000
489/489 [==============================] - 0s 172us/step - loss: 23.2305 - acc: 0.6115 - val_loss: 4.2624 - val_acc: 0.6951
Epoch 10/1000
……
Epoch 1000/1000
489/489 [==============================] - 0s 137us/step - loss: 0.3524 - acc: 0.8200 - val_loss: 0.7290 - val_acc: 0.7012

5.3 分析模型

model.evaluate(x_train, y_train)

489/489 [==============================] - 0s 41us/step
[0.3090217998422728, 0.8548057079315186]

model.evaluate(x_test, y_test)

164/164 [==============================] - 0s 64us/step
[0.7289713301309725, 0.7012194991111755]

plt.plot(history.epoch, history.history.get('val_acc'), c='r', label='val_acc')
plt.plot(history.epoch, history.history.get('acc'), c='b', label='acc')
plt.legend()

6. 正则化

l1：loss = s*abs(w1 + w2 + …) + mse

l2：loss = s*(w12 + w22 + …) + mse

from keras import regularizers

6.1 神经网络太过复杂容易过拟合

#神经网络太过复杂容易过拟合
model = keras.Sequential()
model.add(layers.Dense(128, kernel_regularizer=regularizers.l2(0.001), input_dim=15, activation='relu'))
model.add(layers.Dense(128, kernel_regularizer=regularizers.l2(0.001), activation='relu'))
model.add(layers.Dense(128, kernel_regularizer=regularizers.l2(0.001), activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='adam',
              loss='binary_crossentropy',
              metrics=['acc']
)

history = model.fit(x_train, y_train, epochs=1000, validation_data=(x_test, y_test))

Train on 489 samples, validate on 164 samples
Epoch 1/1000
489/489 [==============================] - 0s 752us/step - loss: 22.2560 - acc: 0.5910 - val_loss: 9.1111 - val_acc: 0.6524
Epoch 2/1000
489/489 [==============================] - 0s 137us/step - loss: 6.8963 - acc: 0.6217 - val_loss: 3.2886 - val_acc: 0.4573
Epoch 3/1000
489/489 [==============================] - 0s 161us/step - loss: 5.0407 - acc: 0.6830 - val_loss: 1.1973 - val_acc: 0.7256
Epoch 4/1000
489/489 [==============================] - 0s 218us/step - loss: 6.6088 - acc: 0.6421 - val_loss: 7.4651 - val_acc: 0.7012
Epoch 5/1000
489/489 [==============================] - 0s 233us/step - loss: 8.3945 - acc: 0.6973 - val_loss: 2.5579 - val_acc: 0.7317
Epoch 6/1000
489/489 [==============================] - 0s 192us/step - loss: 7.0204 - acc: 0.6196 - val_loss: 3.6758 - val_acc: 0.6829
Epoch 7/1000
489/489 [==============================] - 0s 152us/step - loss: 3.9961 - acc: 0.7382 - val_loss: 1.6183 - val_acc: 0.7317
Epoch 8/1000
489/489 [==============================] - 0s 94us/step - loss: 2.3441 - acc: 0.6237 - val_loss: 1.1523 - val_acc: 0.7256
Epoch 9/1000
489/489 [==============================] - 0s 114us/step - loss: 1.8178 - acc: 0.6442 - val_loss: 1.3449 - val_acc: 0.7073
Epoch 10/1000
489/489 [==============================] - 0s 157us/step - loss: 1.6122 - acc: 0.7117 - val_loss: 1.2869 - val_acc: 0.6646
……
Epoch 1000/1000
489/489 [==============================] - 0s 130us/step - loss: 0.1452 - acc: 0.9775 - val_loss: 1.0515 - val_acc: 0.7866
model.evaluate(x_train, y_train)

model.evaluate(x_train, y_train)

489/489 [==============================] - 0s 34us/step
[0.17742264538942426, 0.9611452221870422]

model.evaluate(x_test, y_test)

164/164 [==============================] - 0s 77us/step
[1.0514701096023, 0.7865853905677795]

6.2 太简单容易欠拟合

#太简单容易欠拟合
model = keras.Sequential()
model.add(layers.Dense(4, input_dim=15, activation='relu'))
model.add(layers.Dense(1,  activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='adam',
              loss='binary_crossentropy',
              metrics=['acc']
)

history = model.fit(x_train, y_train, epochs=1000, validation_data=(x_test, y_test))

Train on 489 samples, validate on 164 samples
Epoch 1/1000
489/489 [==============================] - 0s 502us/step - loss: 0.6932 - acc: 0.4765 - val_loss: 0.6931 - val_acc: 0.6341
Epoch 2/1000
489/489 [==============================] - 0s 91us/step - loss: 0.6931 - acc: 0.5174 - val_loss: 0.6930 - val_acc: 0.6341
Epoch 3/1000
489/489 [==============================] - 0s 107us/step - loss: 0.6931 - acc: 0.5174 - val_loss: 0.6924 - val_acc: 0.6341
Epoch 4/1000
489/489 [==============================] - 0s 91us/step - loss: 0.6930 - acc: 0.5174 - val_loss: 0.6916 - val_acc: 0.6341
Epoch 5/1000
489/489 [==============================] - 0s 101us/step - loss: 0.6930 - acc: 0.5174 - val_loss: 0.6914 - val_acc: 0.6341
Epoch 6/1000
489/489 [==============================] - 0s 113us/step - loss: 0.6930 - acc: 0.5174 - val_loss: 0.6914 - val_acc: 0.6341
Epoch 7/1000
489/489 [==============================] - 0s 147us/step - loss: 0.6929 - acc: 0.5174 - val_loss: 0.6908 - val_acc: 0.6341
Epoch 8/1000
489/489 [==============================] - 0s 166us/step - loss: 0.6929 - acc: 0.5174 - val_loss: 0.6905 - val_acc: 0.6341
Epoch 9/1000
489/489 [==============================] - 0s 162us/step - loss: 0.6929 - acc: 0.5174 - val_loss: 0.6904 - val_acc: 0.6341
Epoch 10/1000
489/489 [==============================] - 0s 129us/step - loss: 0.6928 - acc: 0.5174 - val_loss: 0.6901 - val_acc: 0.6341
……
Epoch 1000/1000
489/489 [==============================] - 0s 86us/step - loss: 0.6926 - acc: 0.5174 - val_loss: 0.6849 - val_acc: 0.6341

model.evaluate(x_train, y_train)

489/489 [==============================] - 0s 43us/step
[0.6925447341854587, 0.5173823833465576]

model.evaluate(x_test, y_test)

164/164 [==============================] - 0s 39us/step
[0.684889389247429, 0.6341463327407837]

6.3 选取适当的神经网络

# 选取适当的神经网络
model = keras.Sequential()
model.add(layers.Dense(4, input_dim=15, activation='relu'))
model.add(layers.Dense(4,  activation='relu'))
model.add(layers.Dense(1, activation='sigmoid'))

model.compile(optimizer='adam',
              loss='binary_crossentropy',
              metrics=['acc']
)

history = model.fit(x_train, y_train, epochs=1000, validation_data=(x_test, y_test))

Train on 489 samples, validate on 164 samples
Epoch 1/1000
489/489 [==============================] - 0s 575us/step - loss: 40.1825 - acc: 0.5317 - val_loss: 17.6376 - val_acc: 0.6098
Epoch 2/1000
489/489 [==============================] - 0s 104us/step - loss: 30.0785 - acc: 0.5337 - val_loss: 12.6986 - val_acc: 0.6159
Epoch 3/1000
489/489 [==============================] - 0s 148us/step - loss: 20.0469 - acc: 0.5112 - val_loss: 8.3732 - val_acc: 0.5671
Epoch 4/1000
489/489 [==============================] - 0s 151us/step - loss: 12.5171 - acc: 0.4908 - val_loss: 3.8925 - val_acc: 0.5061
Epoch 5/1000
489/489 [==============================] - 0s 113us/step - loss: 4.4324 - acc: 0.4294 - val_loss: 0.9156 - val_acc: 0.4573
Epoch 6/1000
489/489 [==============================] - 0s 79us/step - loss: 1.0313 - acc: 0.5419 - val_loss: 0.9974 - val_acc: 0.4695
Epoch 7/1000
489/489 [==============================] - 0s 88us/step - loss: 1.0071 - acc: 0.5562 - val_loss: 0.8852 - val_acc: 0.5183
Epoch 8/1000
489/489 [==============================] - 0s 88us/step - loss: 0.9085 - acc: 0.5808 - val_loss: 0.7934 - val_acc: 0.5366
Epoch 9/1000
489/489 [==============================] - 0s 107us/step - loss: 0.8235 - acc: 0.5992 - val_loss: 0.7390 - val_acc: 0.5366
Epoch 10/1000
489/489 [==============================] - 0s 114us/step - loss: 0.7711 - acc: 0.5971 - val_loss: 0.7174 - val_acc: 0.5366
……
Epoch 1000/1000
489/489 [==============================] - 0s 141us/step - loss: 0.3095 - acc: 0.8732 - val_loss: 0.3971 - val_acc: 0.8537

model.evaluate(x_train, y_train)

489/489 [==============================] - 0s 68us/step
[0.30120014958464536, 0.8813905715942383]

model.evaluate(x_test, y_test)

164/164 [==============================] - 0s 45us/step
[0.39714593858253666, 0.8536585569381714]

附：系列文章

序号	文章目录	直达链接
1	波士顿房价预测	https://want595.blog.csdn.net/article/details/132181950
2	鸢尾花数据集分析	https://want595.blog.csdn.net/article/details/132182057
3	特征处理	https://want595.blog.csdn.net/article/details/132182165
4	交叉验证	https://want595.blog.csdn.net/article/details/132182238
5	构造神经网络示例	https://want595.blog.csdn.net/article/details/132182341
6	使用TensorFlow完成线性回归	https://want595.blog.csdn.net/article/details/132182417
7	使用TensorFlow完成逻辑回归	https://want595.blog.csdn.net/article/details/132182496
8	TensorBoard案例	https://want595.blog.csdn.net/article/details/132182584
9	使用Keras完成线性回归	https://want595.blog.csdn.net/article/details/132182723
10	使用Keras完成逻辑回归	https://want595.blog.csdn.net/article/details/132182795
11	使用Keras预训练模型完成猫狗识别	https://want595.blog.csdn.net/article/details/132243928
12	使用PyTorch训练模型	https://want595.blog.csdn.net/article/details/132243989
13	使用Dropout抑制过拟合	https://want595.blog.csdn.net/article/details/132244111
14	使用CNN完成MNIST手写体识别(TensorFlow)	https://want595.blog.csdn.net/article/details/132244499
15	使用CNN完成MNIST手写体识别(Keras)	https://want595.blog.csdn.net/article/details/132244552
16	使用CNN完成MNIST手写体识别(PyTorch)	https://want595.blog.csdn.net/article/details/132244641
17	使用GAN生成手写数字样本	https://want595.blog.csdn.net/article/details/132244764
18	自然语言处理	https://want595.blog.csdn.net/article/details/132276591

你可能感兴趣的:(《,深度学习,》,python,深度学习,开发语言)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
理解Gunicorn：Python WSGI服务器的基石范范0825 ipython linux 运维
理解Gunicorn：PythonWSGI服务器的基石介绍Gunicorn，全称GreenUnicorn，是一个为PythonWSGI（WebServerGatewayInterface）应用设计的高效、轻量级HTTP服务器。作为PythonWeb应用部署的常用工具，Gunicorn以其高性能和易用性著称。本文将介绍Gunicorn的基本概念、安装和配置，帮助初学者快速上手。1.什么是Gunico
Python数据分析与可视化实战指南 William数据分析 python python 数据
在数据驱动的时代，Python因其简洁的语法、强大的库生态系统以及活跃的社区，成为了数据分析与可视化的首选语言。本文将通过一个详细的案例，带领大家学习如何使用Python进行数据分析，并通过可视化来直观呈现分析结果。一、环境准备1.1安装必要库在开始数据分析和可视化之前，我们需要安装一些常用的库。主要包括pandas、numpy、matplotlib和seaborn等。这些库分别用于数据处理、数学
python os.environ 江湖偌大 python 深度学习
os.environ['TF_CPP_MIN_LOG_LEVEL']='0'#默认值，输出所有信息os.environ['TF_CPP_MIN_LOG_LEVEL']='1'#屏蔽通知信息（INFO）os.environ['TF_CPP_MIN_LOG_LEVEL']='2'#屏蔽通知信息和警告信息（INFO\WARNING）os.environ['TF_CPP_MIN_LOG_LEVEL']='
Python中os.environ基本介绍及使用方法鹤冲天Pro #Python python 服务器开发语言
文章目录python中os.environos.environ简介os.environ进行环境变量的增删改查python中os.environ的使用详解1.简介2.key字段详解2.1常见key字段3.os.environ.get()用法4.环境变量的增删改查和判断是否存在4.1新增环境变量4.2更新环境变量4.3获取环境变量4.4删除环境变量4.5判断环境变量是否存在python中os.envi
Pyecharts数据可视化大屏：打造沉浸式数据分析体验我的运维人生信息可视化数据分析数据挖掘运维开发技术共享
Pyecharts数据可视化大屏：打造沉浸式数据分析体验在当今这个数据驱动的时代，如何将海量数据以直观、生动的方式展现出来，成为了数据分析师和企业决策者关注的焦点。Pyecharts，作为一款基于Python的开源数据可视化库，凭借其丰富的图表类型、灵活的配置选项以及高度的定制化能力，成为了构建数据可视化大屏的理想选择。本文将深入探讨如何利用Pyecharts打造数据可视化大屏，并通过实际代码案例
Python教程：一文了解使用Python处理XPath 旦莫 Python进阶 python 开发语言
目录1.环境准备1.1安装lxml1.2验证安装2.XPath基础2.1什么是XPath？2.2XPath语法2.3示例XML文档3.使用lxml解析XML3.1解析XML文档3.2查看解析结果4.XPath查询4.1基本路径查询4.2使用属性查询4.3查询多个节点5.XPath的高级用法5.1使用逻辑运算符5.2使用函数6.实战案例6.1从网页抓取数据6.1.1安装Requests库6.1.2代
python os.environ_python os.environ 读取和设置环境变量 weixin_39605414 python os.environ
>>>importos>>>os.environ.keys()['LC_NUMERIC','GOPATH','GOROOT','GOBIN','LESSOPEN','SSH_CLIENT','LOGNAME','USER','HOME','LC_PAPER','PATH','DISPLAY','LANG','TERM','SHELL','J2REDIR','LC_MONETARY','QT_QPA
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
使用Faiss进行高效相似度搜索 llzwxh888 faiss python
在现代AI应用中，快速和高效的相似度搜索是至关重要的。Faiss（FacebookAISimilaritySearch）是一个专门用于快速相似度搜索和聚类的库，特别适用于高维向量。本文将介绍如何使用Faiss来进行相似度搜索，并结合Python代码演示其基本用法。什么是Faiss？Faiss是一个由FacebookAIResearch团队开发的开源库，主要用于高维向量的相似性搜索和聚类。Faiss
python是什么意思中文-在python中%是什么意思编程大乐趣
Python中%有两种：1、数值运算：%代表取模，返回除法的余数。如：>>>7%212、%操作符（字符串格式化，stringformatting），说明如下：%[(name)][flags][width].[precision]typecode(name)为命名flags可以有+，-，''或0。+表示右对齐。-表示左对齐。''为一个空格，表示在正数的左侧填充一个空格，从而与负数对齐。0表示使用0填
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
python八股文面试题分享及解析(1) Shawn________ python
#1.'''a=1b=2不用中间变量交换a和b'''#1.a=1b=2a,b=b,aprint(a)print(b)结果：21#2.ll=[]foriinrange(3):ll.append({'num':i})print(11)结果:#[{'num':0},{'num':1},{'num':2}]#3.kk=[]a={'num':0}foriinrange(3):#0,12#可变类型，不仅仅改变
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
Python快速入门 —— 第三节：类与对象孤华暗香 Python快速入门 python 开发语言
第三节：类与对象目标：了解面向对象编程的基础概念，并学会如何定义类和创建对象。内容：类与对象：定义类：class关键字。类的构造函数：__init__()。类的属性和方法。对象的创建与使用。示例：classStudent:def__init__(self,name,age,major):self.name&#
pyecharts——绘制柱形图折线图 2224070247 信息可视化 python java 数据可视化
一、pyecharts概述自2013年6月百度EFE(ExcellentFrontEnd）数据可视化团队研发的ECharts1.0发布到GitHub网站以来，ECharts一直备受业界权威的关注并获得广泛好评，成为目前成熟且流行的数据可视化图表工具，被应用到诸多数据可视化的开发领域。Python作为数据分析领域最受欢迎的语言，也加入ECharts的使用行列，并研发出方便Python开发者使用的数据
Python 实现图片裁剪（附代码） | Python工具剑客阿良_ALiang
前言本文提供将图片按照自定义尺寸进行裁剪的工具方法，一如既往的实用主义。环境依赖ffmpeg环境安装，可以参考我的另一篇文章：windowsffmpeg安装部署_阿良的博客-CSDN博客本文主要使用到的不是ffmpeg，而是ffprobe也在上面这篇文章中的zip包中。ffmpy安装：pipinstallffmpy-ihttps://pypi.douban.com/simple代码不废话了，上代码
【华为OD技术面试真题 - 技术面】- python八股文真题题库（4) 算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选**1.Python中的`with`**用途和功能自动资源管理示例：文件操作上下文管理协议示例代码工作流程解析优点2.\_\_new\_\_和**\_\_init\_\_**区别__new____init__区别总结3.**切片（Slicing）操作**基本切片语法
python os 环境变量 CV矿工 python 开发语言 numpy
环境变量：环境变量是程序和操作系统之间的通信方式。有些字符不宜明文写进代码里，比如数据库密码，个人账户密码，如果写进自己本机的环境变量里，程序用的时候通过os.environ.get（）取出来就行了。os.environ是一个环境变量的字典。环境变量的相关操作importos"""设置/修改环境变量：os.environ[‘环境变量名称’]=‘环境变量值’#其中key和value均为string类
Python爬虫解析工具之xpath使用详解 eqa11 python 爬虫开发语言
文章目录Python爬虫解析工具之xpath使用详解一、引言二、环境准备1、插件安装2、依赖库安装三、xpath语法详解1、路径表达式2、通配符3、谓语4、常用函数四、xpath在Python代码中的使用1、文档树的创建2、使用xpath表达式3、获取元素内容和属性五、总结Python爬虫解析工具之xpath使用详解一、引言在Python爬虫开发中，数据提取是一个至关重要的环节。xpath作为一门
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
《Python数据分析实战终极指南》 xjt921122 python 数据分析开发语言
对于分析师来说，大家在学习Python数据分析的路上，多多少少都遇到过很多大坑**，有关于技能和思维的**：Excel已经没办法处理现有的数据量了，应该学Python吗？找了一大堆Python和Pandas的资料来学习，为什么自己动手就懵了？跟着比赛类公开数据分析案例练了很久，为什么当自己面对数据需求还是只会数据处理而没有分析思路？学了对比、细分、聚类分析，也会用PEST、波特五力这类分析法，为啥
Python中深拷贝与浅拷贝的区别 yuxiaoyu.
转自：http://blog.csdn.net/u014745194/article/details/70271868定义：在Python中对象的赋值其实就是对象的引用。当创建一个对象，把它赋值给另一个变量的时候，python并没有拷贝这个对象，只是拷贝了这个对象的引用而已。浅拷贝：拷贝了最外围的对象本身，内部的元素都只是拷贝了一个引用而已。也就是，把对象复制一遍，但是该对象中引用的其他对象我不复
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python编译器鹿鹿~ Python编译器 Python python 开发语言后端
嘿嘿嘿我又来了啊有些小盆友可能不知道Python其实是有编译器的，也就是PyCharm。你们可能会问到这个是干嘛的又不可以吃也不可以穿好像没有什么用，其实你还说对了这个还真的不可以吃也不可以穿，但是它用来干嘛的呢。用来编译你所打出的代码进行运行（可能这里说的有点不对但是只是个人认为）现在我们来说说PyCharm是用来干嘛的。PyCharm是一种PythonIDE，带有一整套可以帮助用户在使用Pyt
一文掌握python面向对象魔术方法（二）程序员neil python python 开发语言
接上篇：一文掌握python面向对象魔术方法（一）-CSDN博客目录六、迭代和序列化：1、__iter__(self):定义迭代器，使得类可以被for循环迭代。2、__getitem__(self,key):定义索引操作，如obj[key]。3、__setitem__(self,key,value):定义赋值操作，如obj[key]=value。4、__delitem__(self,key):定义
一文掌握python常用的list（列表）操作程序员neil python python 开发语言
目录一、创建列表1.直接创建列表：2.使用list()构造器3.使用列表推导式4.创建空列表二、访问列表元素1.列表支持通过索引访问元素，索引从0开始：2.还可以使用切片操作访问列表的一部分：三、修改列表元素四、添加元素1.append()：在末尾添加元素2.insert()：在指定位置插入元素五、删除元素1.del：删除指定位置的元素2.remove()：删除指定值的第一个匹配项3.pop()：
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
python中的深拷贝与浅拷贝 anshejd70787 python
深拷贝和浅拷贝浅拷贝的时候，修改原来的对象，浅拷贝的对象不会发生改变。1、对象的赋值对象的赋值实际上是对象之间的引用：当创建一个对象，然后将这个对象赋值给另外一个变量的时候，python并没有拷贝这个对象，而只是拷贝了这个对象的引用。当对对象做赋值或者是参数传递或者作为返回值的时候，总是传递原始对象的引用，而不是一个副本。如下所示：>>>aList=["kel","abc",123]>>>bLis
LeetCode[Math] - #66 Plus One Cwind java LeetCode 题解 Algorithm Math
原题链接：#66 Plus One 要求：给定一个用数字数组表示的非负整数，如num1 = {1, 2, 3, 9}, num2 = {9, 9}等，给这个数加上1。注意： 1. 数字的较高位存在数组的头上，即num1表示数字1239 2. 每一位（数组中的每个元素）的取值范围为0~9 难度：简单分析：题目比较简单，只须从数组
JQuery中$.ajax()方法参数详解 AILIKES JavaScript jsonp jquery Ajax json
url: 要求为String类型的参数，（默认为当前页地址）发送请求的地址。 type: 要求为String类型的参数，请求方式（post或get）默认为get。注意其他http请求方法，例如put和 delete也可以使用，但仅部分浏览器支持。 timeout: 要求为Number类型的参数，设置请求超时时间（毫秒）。此设置将覆盖$.ajaxSetup()方法的全局
JConsole & JVisualVM远程监视Webphere服务器JVM Kai_Ge JVisualVM JConsole Webphere
JConsole是JDK里自带的一个工具，可以监测Java程序运行时所有对象的申请、释放等动作，将内存管理的所有信息进行统计、分析、可视化。我们可以根据这些信息判断程序是否有内存泄漏问题。　　使用JConsole工具来分析WAS的JVM问题，需要进行相关的配置。　　首先我们看WAS服务器端的配置. 　　1、登录was控制台https://10.4.119.18
自定义annotation 120153216 annotation
Java annotation 自定义注释@interface的用法一、什么是注释说起注释，得先提一提什么是元数据(metadata)。所谓元数据就是数据的数据。也就是说，元数据是描述数据的。就象数据表中的字段一样，每个字段描述了这个字段下的数据的含义。而J2SE5.0中提供的注释就是java源代码的元数据，也就是说注释是描述java源
CentOS 5/6.X 使用 EPEL YUM源 2002wmj centos
CentOS 6.X 安装使用EPEL YUM源1. 查看操作系统版本[root@node1 ~]# uname -a Linux node1.test.com 2.6.32-358.el6.x86_64 #1 SMP Fri Feb 22 00:31:26 UTC 2013 x86_64 x86_64 x86_64 GNU/Linux [root@node1 ~]#
在SQLSERVER中查找缺失和无用的索引SQL 357029540 SQL Server
--缺失的索引 SELECT avg_total_user_cost * avg_user_impact * ( user_scans + user_seeks ) AS PossibleImprovement , last_user_seek ,
Spring3 MVC 笔记（二） —json+rest优化 7454103 Spring3 MVC
接上次的 spring mvc 注解的一些详细信息！其实也是一些个人的学习笔记呵呵！
替换“\”的时候报错Unexpected internal error near index 1 \ ^ adminjun java “\替换”
发现还是有些东西没有刻子脑子里,,过段时间就没什么概念了,所以贴出来...以免再忘... 在拆分字符串时遇到通过 \ 来拆分，可是用所以想通过转义 \\ 来拆分的时候会报异常 public class Main { /*
POJ 1035 Spell checker(哈希表) aijuans 暴力求解--哈希表
/* 题意：输入字典，然后输入单词，判断字典中是否出现过该单词，或者是否进行删除、添加、替换操作，如果是，则输出对应的字典中的单词要求按照输入时候的排名输出题解：建立两个哈希表。一个存储字典和输入字典中单词的排名，一个进行最后输出的判重 */ #include <iostream> //#define using namespace std; const int HASH =
通过原型实现javascript Array的去重、最大值和最小值 ayaoxinchao JavaScript array prototype
用原型函数（prototype）可以定义一些很方便的自定义函数，实现各种自定义功能。本次主要是实现了Array的去重、获取最大值和最小值。实现代码如下： <script type="text/javascript"> Array.prototype.unique = function() { var a = {}; var le
UIWebView实现https双向认证请求 bewithme UIWebView https Objective-C
什么是HTTPS双向认证我已在先前的博文 ASIHTTPRequest实现https双向认证请求中有讲述，不理解的读者可以先复习一下。本文是用UIWebView来实现对需要客户端证书验证的服务请求，网上有些文章中有涉及到此内容，但都只言片语，没有讲完全，更没有完整的代码，让人困扰不已。但是此知
NoSQL数据库之Redis数据库管理(Redis高级应用之事务处理、持久化操作、pub_sub、虚拟内存) bijian1013 redis 数据库 NoSQL
3.事务处理 Redis对事务的支持目前不比较简单。Redis只能保证一个client发起的事务中的命令可以连续的执行，而中间不会插入其他client的命令。当一个client在一个连接中发出multi命令时，这个连接会进入一个事务上下文，该连接后续的命令不会立即执行，而是先放到一个队列中，当执行exec命令时，redis会顺序的执行队列中
各数据库分页sql备忘 bingyingao oracle sql 分页
ORACLE 下面这个效率很低 SELECT * FROM ( SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_FS_RETURN order by id desc) A ) WHERE RN <20; 下面这个效率很高 SELECT A.*, ROWNUM RN FROM (SELECT * FROM IPAY_RCD_
【Scala七】Scala核心一：函数 bit1129 scala
1. 如果函数体只有一行代码，则可以不用写{},比如 def print(x: Int) = println(x) 一行上的多条语句用分号隔开，则只有第一句属于方法体，例如 def printWithValue(x: Int) : String= println(x); "ABC" 上面的代码报错，因为，printWithValue的方法
了解GHC的factorial编译过程 bookjovi haskell
GHC相对其他主流语言的编译器或解释器还是比较复杂的，一部分原因是haskell本身的设计就不易于实现compiler，如lazy特性，static typed，类型推导等。关于GHC的内部实现有篇文章说的挺好，这里，文中在RTS一节中详细说了haskell的concurrent实现，里面提到了green thread，如果熟悉Go语言的话就会发现，ghc的concurrent实现和Go有点类
Java-Collections Framework学习与总结-LinkedHashMap BrokenDreams LinkedHashMap
前面总结了java.util.HashMap，了解了其内部由散列表实现，每个桶内是一个单向链表。那有没有双向链表的实现呢？双向链表的实现会具备什么特性呢？来看一下HashMap的一个子类——java.util.LinkedHashMap。
读《研磨设计模式》-代码笔记-抽象工厂模式-Abstract Factory bylijinnan abstract
声明：本文只为方便我个人查阅和理解，详细的分析以及源代码请移步原作者的博客http://chjavach.iteye.com/ package design.pattern; /* * Abstract Factory Pattern * 抽象工厂模式的目的是： * 通过在抽象工厂里面定义一组产品接口，方便地切换“产品簇” * 这些接口是相关或者相依赖的
压暗面部高光 cherishLC PS
方法一、压暗高光&重新着色当皮肤很油又使用闪光灯时，很容易在面部形成高光区域。下面讲一下我今天处理高光区域的心得：皮肤可以分为纹理和色彩两个属性。其中纹理主要由亮度通道（Lab模式的L通道）决定，色彩则由a、b通道确定。处理思路为在保持高光区域纹理的情况下，对高光区域着色。具体步骤为：降低高光区域的整体的亮度，再进行着色。如果想简化步骤，可以只进行着色（参看下面的步骤1
Java VisualVM监控远程JVM crabdave visualvm
Java VisualVM监控远程JVM JDK1.6开始自带的VisualVM就是不错的监控工具. 这个工具就在JAVA_HOME\bin\目录下的jvisualvm.exe, 双击这个文件就能看到界面通过JMX连接远程机器, 需要经过下面的配置: 1. 修改远程机器JDK配置文件 (我这里远程机器是linux).
Saiku去掉登录模块 daizj saiku 登录 olap BI
1、修改applicationContext-saiku-webapp.xml <security:intercept-url pattern="/rest/**" access="IS_AUTHENTICATED_ANONYMOUSLY" /> <security:intercept-url pattern=&qu
浅析 Flex中的Focus dsjt html Flex Flash
关键字：focus、 setFocus、 IFocusManager、KeyboardEvent 焦点、设置焦点、获得焦点、键盘事件一、无焦点的困扰——组件监听不到键盘事件原因：只有获得焦点的组件（确切说是InteractiveObject）才能监听到键盘事件的目标阶段；键盘事件（flash.events.KeyboardEvent）参与冒泡阶段，所以焦点组件的父项（以及它爸
Yii全局函数使用 dcj3sjt126com yii
由于YII致力于完美的整合第三方库，它并没有定义任何全局函数。yii中的每一个应用都需要全类别和对象范围。例如，Yii::app()->user;Yii::app()->params['name'];等等。我们可以自行设定全局函数，使得代码看起来更加简洁易用。(原文地址) 我们可以保存在globals.php在protected目录下。然后，在入口脚本index.php的，我们包括在
设计模式之单例模式二（解决无序写入的问题） come_for_dream 单例模式 volatile 乱序执行双重检验锁
在上篇文章中我们使用了双重检验锁的方式避免懒汉式单例模式下由于多线程造成的实例被多次创建的问题，但是因为由于JVM为了使得处理器内部的运算单元能充分利用，处理器可能会对输入代码进行乱序执行（Out Of Order Execute）优化，处理器会在计算之后将乱序执行的结果进行重组，保证该
程序员从初级到高级的蜕变 gcq511120594 框架工作 PHP android html5
软件开发是一个奇怪的行业，市场远远供不应求。这是一个已经存在多年的问题，而且随着时间的流逝，愈演愈烈。我们严重缺乏能够满足需求的人才。这个行业相当年轻。大多数软件项目是失败的。几乎所有的项目都会超出预算。我们解决问题的最佳指导方针可以归结为——“用一些通用方法去解决问题，当然这些方法常常不管用，于是，唯一能做的就是不断地尝试，逐个看看是否奏效”。现在我们把淫浸代码时间超过3年的开发人员称为
Reverse Linked List hcx2013 list
Reverse a singly linked list. /** * Definition for singly-linked list. * public class ListNode { * int val; * ListNode next; * ListNode(int x) { val = x; } * } */ p
Spring4.1新特性——数据库集成测试 jinnianshilongnian spring 4.1
目录 Spring4.1新特性——综述 Spring4.1新特性——Spring核心部分及其他 Spring4.1新特性——Spring缓存框架增强 Spring4.1新特性——异步调用和事件机制的异常处理 Spring4.1新特性——数据库集成测试脚本初始化 Spring4.1新特性——Spring MVC增强 Spring4.1新特性——页面自动化测试框架Spring MVC T
C# Ajax上传图片同时生成微缩图(附Demo) liyonghui160com
1.Ajax无刷新上传图片,详情请阅我的这篇文章。（jquery + c# ashx） 2.C#位图处理 System.Drawing。 3.最新demo支持IE7,IE8,Fir
Java list三种遍历方法性能比较 pda158 java
从c/c++语言转向java开发，学习java语言list遍历的三种方法，顺便测试各种遍历方法的性能，测试方法为在ArrayList中插入1千万条记录，然后遍历ArrayList，发现了一个奇怪的现象，测试代码例如以下： package com.hisense.tiger.list; import java.util.ArrayList; import java.util.Iterator;
300个涵盖IT各方面的免费资源（上）——商业与市场篇 shoothao seo 商业与市场 IT资源免费资源
A.网站模板+logo+服务器主机+发票生成 HTML5 UP:响应式的HTML5和CSS3网站模板。 Bootswatch:免费的Bootstrap主题。 Templated:收集了845个免费的CSS和HTML5网站模板。 Wordpress.org|Wordpress.com:可免费创建你的新网站。 Strikingly:关注领域中免费无限的移动优
localStorage、sessionStorage uule localStorage
W3School 例子 HTML5 提供了两种在客户端存储数据的新方法： localStorage - 没有时间限制的数据存储 sessionStorage - 针对一个 session 的数据存储之前，这些都是由 cookie 完成的。但是 cookie 不适合大量数据的存储，因为它们由每个对服务器的请求来传递，这使得 cookie 速度很慢而且效率也不