快速排序和归并排序的非递归形式

        快速排序和归并排序都需要用递归的形式展开，那么有没有什么方法不需要递归就能实现归并和快速排序，有的！

 1.快速排序

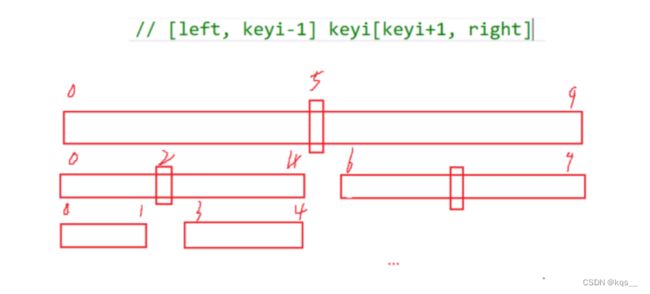
        我们可以借助栈来模拟递归。

        递归的主要思想就是大事化小，小事化了。我们借助栈的 目的是将需要排序的“头” 和 “尾”找到，进而排序，然后找到合适的keyi并放入合适的位置，再将keyi两边的“头” 和 “尾”入栈，找到合适的keyi......如此重复下去.......

        keyi需要入栈吗？keyi不需要入栈，因为keyi已经在合适的位置了

前后指针法，结合上一篇博客来看， 

int PatrSort3(int* a, int begin, int end)
{

	int prev = begin, cur = begin+1;

	int keyi = begin;

	int midi = GetMidIndex(a , begin ,end);
	Swap(&a[keyi],&a[midi]);

	while (cur <= end)
	{
		//cur位置小于keyi发生交换
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			//++prev;
			Swap(&a[prev], &a[cur]);
		}

		cur++;
	}

	Swap(&a[keyi],&a[prev]);

	keyi = prev;
	return keyi;

}

void QuickSortNonR(int* a, int begin, int end)
{
	ST st;
	STInit(&st);
	STPush(&st,end);
	STPush(&st, begin);

	while (!STEmpty(&st))
	{
		int left = STTop(&st);
		STPop(&st);

		int right = STTop(&st);
		STPop(&st);

		int keyi = PatrSort3(a,left,right);

		if (keyi + 1 < right)
		{
			STPush(&st,right);
			STPush(&st,keyi+1);
		}

		if (left < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, left);
		}

	}

	STDestroy(&st);
}

2.归并排序

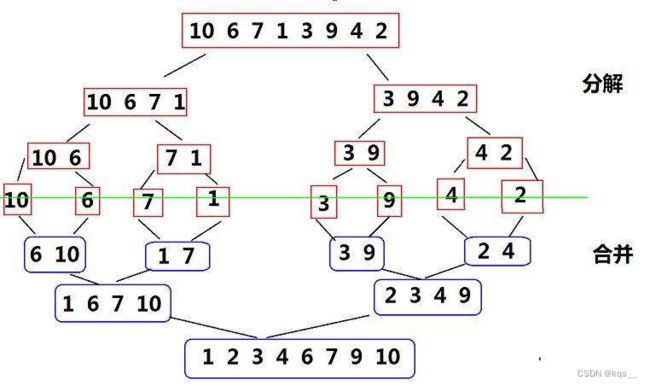
        归并排序的基本思想在上一篇已经讲过，快速排序是先对整个数组中选出适中的的keyi，放到合适的位置，然后切分子块，层层递归，进行排序，快速排序类似于前序遍历。归并排序是先找到最小的子块，然后层层排序，层层归并,归并排序类似于后序遍历。

        归并排序还存在越界的问题：每个子区间应该怎么样确定，能给出明确的边界吗？

        边界是怎么确定的：

 

        gap每次增加是上一次的2倍，当gap = 4 时， 数组有10个元素，我们控制循环是按照一下的方式来控制的。

        当 i = 0 的时候 begin1 end1 ，begin2 end2 。[0 ,3]  [4 ,7]  。

        进入下一轮循环： i = 8 ， begin1 end1 ，begin2 end2 。[8,11]  [12 ,15] 。

 

        此时问题来了，数组只有十个元素，下标为 10-15  已经越界访问了 ，这是我们要处理越界访问问题。

        

void MergeSortNonR(int* a, int n)
{

	int* tmp = (int*)malloc(sizeof(int) * n);
	if (tmp == NULL)
	{
		perror("malloc fail");
	}

	int gap = 1;
	while (gap < n)
	{
		printf("gap:%d->", gap);
		for (int i = 0; i < n; i += 2*gap)
		{

		
			//[i,i+gap-1] [i+gap ,i + 2*gap-1] 控制边界
			int begin1 = i;
			int end1 = i + gap - 1;
			int begin2 = i + gap;
			int end2 = i + 2 * gap - 1;


			//越界，修正边界
			if (end1 >= n)
			{
				end1 = n - 1;

				// [begin2, end2]修正为不存在区间
				begin2 = n;
				end2 = n - 1;
			}
			else if (begin2 >=n)
			{
			// [begin2, end2]修正为不存在区间
				begin2 = n;
				end2 = n - 1;
			}
			else if (end2 >= n)
			{
				end2 = n - 1;
			}

			printf("[%d,%d] [%d, %d]--", begin1, end1, begin2, end2);

			int m = end2 - begin1+1;
			int j = begin1;

 			while (begin1 <= end1 && begin2 <= end2)
			{
				if (a[begin1] < a[begin2])
				{
					tmp[j++] = a[begin1++];
				}
				else
				{
					tmp[j++] = a[begin2++];
				}
			}

			while (begin1 <= end1)
			{
				tmp[j++] = a[begin1++];
			}

			while (begin2 <= end2)
			{
				tmp[j++] = a[begin2++];
			}
			
		memcpy(a+i, tmp+i, sizeof(int) * m);


		}
	//	memcpy(a, tmp, sizeof(int) * m);
	
		printf("\n");
		
		gap *= 2;
 	}

	free(tmp);

}

void TestMergeSort()
{
	int a[] = { 9, 1, 2, 5, 7, 4, 8, 6, 3, 5 };
	//MergeSort(a, sizeof(a) / sizeof(int) );
	MergeSortNonR(a, sizeof(a) / sizeof(int));
	PrintArray(a, sizeof(a) / sizeof(int));
}

归并排序的特性总结：
        1. 归并的缺点在于需要O(N)的空间复杂度，归并排序的思考更多的是解决在磁盘中的外排序问题。
        2. 时间复杂度：O(N*logN)
        3. 空间复杂度：O(N)
        4. 稳定性：稳定