风控建模常用指标
一、KS指标
KS常用于评估模型区分度,区分度越大,说明模型的风险排序能力越强
计算逻辑
step 1 对变量进行分箱,可以选择等频、等距,或者自定义距离(不同分箱对ks也会有影响)
step 2 计算每个分箱区间的好账户数和坏账户数
step 3 计算每个分箱区间的累计好账户数占总好账户数比率和累计坏账户数占总坏账户数比率
step 4 计算每个分箱区间累计坏账户占比与累计好账户占比差的绝对值,得到KS曲线
step 5 在这些绝对值中取最大值,得到此变量最终的KS值。
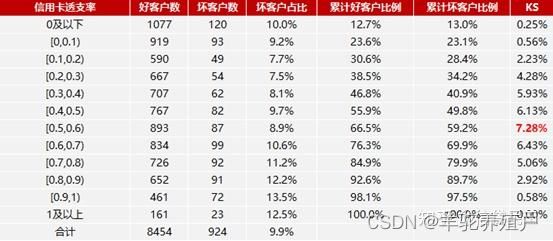
KS值的取值范围是[0,1],一般习惯乘以100%。通常来说,KS越大,表明正负样本区分程度越好。
正常经验取值范围
20%以下:不建议采用
20%-40%:较好
40%-50%:良好
50%-60%:很强
60%-75%:非常强
75%以上:强的离谱,注意检测
注意:不同公司的ks要求不一致,比如我们公司之前ks水平在0.3左右,后一直衰减,去年基本在0.25左右,今年0.17左右模型也在使用
二、psi指标
step 1 将变量预期分布(建模时的分布或上一个周期的分布,记为E)进行分箱离散化,统计各个分箱里的样本占比(每个分箱内发生逾期的占每个分箱内总数的比)
注意:
a)分箱可以是等频、等距或其他方式,分箱方式不同,将导致计算结果略微有差异
b)对于连续型变量(特征变量、模型分数等),分箱数需要设置合理,一般设为10或20;对于离散型变量,如果分箱太多可以提前考虑合并小分箱;分箱数太多,可能会导致每个分箱大的样本量太少而失去统计意义;分箱数太少,又会导致计算结果精度降低。*
step 2 按相同分箱区间,对实际分布 (最新的分布,记为 A A A )统计各分箱内的样本占比。
step 3 计算各分箱内的 A − E A - E A−E ( E E E是)和 L n ( A / E ) Ln(A/E) Ln(A/E) ,然后计算 i n d e x = ( 实际占比 − 预期占比 ) ∗ l n ( 实际占比 / 预期占比 ) index =(实际占比-预期占比)*ln(实际占比/预期占比) index=(实际占比−预期占比)∗ln(实际占比/预期占比)。
step 4 将各分箱的index进行求和,即得到最终的PSI。
PSI数值越小,两个分布之间的差异就越小,代表越稳定
正常经验取值范围
0-0.1 好 没有变化或很小的变化
0.1-0.25略不稳定有变化,继续监控后续变动
大于0.25不稳定发生大变化,进行特征项分析
注意:对于变量特征类上述范围基本适用,对于模型评分,一般分为两种情况
a)、没有数据成本的评分:此类评分的特点是由于没有数据成本,因此不管后面是否会拒绝都会全调,一般使用申请样本计算,计算时psi会更为稳定,首月0.004,三月后0.03,建议阈值定在0.05,而不是0.1;
b)、有成本的评分:此类评分的特点是按需调用,部分拒绝的样本会没有值因而被过滤掉,因此一般用放款样本计算,把上线后首月的分布作为基准,而且会随着策略变动产生影响,建议阈值定在0.1
三、woe\iv指标
(1)IV值可以衡量各变量对y的预测能力,用于筛选变量。
(2) 对离散型变量woe可以观察各个level间的跳转对odds的提升是否呈线性,而IV可以衡量变量整体(而不是每个level)的预测能力
(3) 对连续型变量woe和IV值为分箱的合理性提供了一定的依据。
(4)用woe编码可以处理缺失值问题。
计算逻辑
W O E = l n ( A i / A t B i / B t ) WOE=ln(\frac{A_i/A_t}{B_i/B_t}) WOE=ln(Bi/BtAi/At)
A i A_i Ai 是第 i i i 箱中坏客户的人数
B i B_i Bi 是第 i i i 箱中好客户人数
A t A_t At 是总共坏客户人数
B t B_t Bt 是总共好客户人数
处理分箱中没有响应样本或者全部是响应样本时,可修正为:
W O E = l n ( ( A i + 0.5 ) / A t ( B i + 0.5 ) / B t ) WOE=ln(\frac{(A_i+0.5)/A_t}{(B_i+0.5)/B_t}) WOE=ln((Bi+0.5)/Bt(Ai+0.5)/At)
iv的计算逻辑为
∑ i = 1 n ( ( A i / A t ) − ( B i / B t ) ) ⋅ W O E ) \sum_{i=1}^{n} ((A_i/A_t)-(B_i/B_t)) \cdot WOE) i=1∑n((Ai/At)−(Bi/Bt))⋅WOE)
注意:woe是每个分箱的woe,iv是这个特征整体的iv
注意:
逻辑回归中为什么要使用WOE编码:
1、优化特征表达:
WOE将特征的原始值映射到新的值,这些新的值反映了特征与目标变量之间的关系。通过WOE转换,特征的信息可以更好地被逻辑回归模型利用,从而提高模型的性能。
2、解决线性不可分的问题:
逻辑回归是一个线性模型,要求特征与目标变量之间的关系是线性的。但实际上,特征与目标变量的关系可能是非线性的。WOE转换可以将非线性关系转化为线性关系,使得逻辑回归能更好地拟合数据。
3、稳定建模效果:
WOE可以减小特征中极端值的影响,使得模型更稳定。它将特征划分为多个分箱(bin),对每个分箱计算WOE值,进而将特征的原始值替换为对应分箱的WOE值,避免了特征中极端值的干扰。
4、处理缺失值:
WOE可以单独对缺失值进行分箱并赋予WOE值,这样就能有效地处理缺失值。
正常经验取值范围
iv常用来评估变量的预测能力小于
0.02 几乎没有预测效果
0.02-0.1弱预测效果
0.1-03中等预测效果
0.3-0.5 强测效果
大于0.5 强的离谱,需要确认
正常按拥有的变量整体效果确定,如果说整体没几个好一点的变量,那么选取一些0.015左右的也是可以的;对于类似黑名单数据这种分布的特征,最好不要入模,如果计划入模那么这些特征是不能靠iv筛出来的,最好人工过一遍,因为特征有值的数据太少导致iv很低
四、AUC指标
指标释义
1、几何的角度:AUC指ROC曲线下方的面积大小
2、概率的角度:auc 等价于随机抽取一个正样本和一个负样本,然后用训练得到的分类器来对这两个样本进行预测,预测得到正样本排在负样本之前的概率。
计算逻辑
A U C = ∑ i = 1 P r a n k i − P ( P + 1 ) 2 P × N AUC = \frac{\sum_{i=1}^{P}rank_i - \frac{P(P+1)}{2}}{P\times N} AUC=P×N∑i=1Pranki−2P(P+1)
其中,
r a n k i rank_i ranki 表示第 i i i 个正样本的预测排名,
P P P 表示正样本的数量,
N N N 表示负样本的数量
正常经验取值范围
从AUC 判断分类器(预测模型)优劣的标准:
AUC = 1,是完美分类器。
AUC = [0.85, 0.95], 效果很好
AUC = [0.7, 0.85], 效果一般
AUC = [0.5, 0.7],效果较低,但用于预测股票已经很不错了
AUC = 0.5,跟随机猜测一样(例:丢铜板),模型没有预测价值。
AUC < 0.5,比随机猜测还差;但只要总是反预测而行,就优于随机猜测。
五、lift指标
TP(实际为正预测为正)
FP(实际为负但预测为正)
TN(实际为负预测为负)
FN(实际为正但预测为负)
准确率(accuracy,ACC):
A C C = T P + T N F P + F N + T P + T N ACC = \frac{TP+TN}{FP+FN+TP+TN} ACC=FP+FN+TP+TNTP+TN
正确率(Precision,PRE),查准率:
P R E = T P T P + F P PRE = \frac{TP}{TP+FP} PRE=TP+FPTP
真阳性率(True Positive Rate,TPR),灵敏度(Sensitivity),召回率(Recall):
T P R = T P T P + F N TPR = \frac{TP}{TP+FN} TPR=TP+FNTP
假阳性率(False Positice Rate,FPR),误诊率( = 1 - 特异度):
F P R = F P F P + T N FPR = \frac{FP}{FP+TN} FPR=FP+TNFP
L I F T = T P T P + F P T P + F N T P + F P + T N + F N LIFT = \frac{\frac{TP}{TP+FP}}{\frac{TP+FN}{TP+FP+TN+FN}} LIFT=TP+FP+TN+FNTP+FNTP+FPTP
简单理解为,在这一分箱中,逾期水平是整体逾期水平的多少倍
六、VIF
VIF(方差膨胀因子)是一种用于检测回归模型中自变量间多重共线性的统计方法。它衡量了每个自变量与其他自变量的相关性,可以帮助我们判断是否存在共线性问题。
VIF的计算公式为
VIF ( X i ) = 1 1 − R i 2 \text{VIF}(X_i) = \frac{1}{1 - R_{i}^{2}} VIF(Xi)=1−Ri21。
其中, VIF ( X i ) \text{VIF}(X_i) VIF(Xi) 表示自变量 X i X_i Xi 的方差膨胀因子, R i 2 R_{i}^{2} Ri2 表示将自变量 X i X_i Xi 作为因变量,对其他自变量进行回归所得的决定系数(即拟合优度)。
VIF值的解释如下:
如果 VIF ( X i ) > 1 \text{VIF}(X_i) > 1 VIF(Xi)>1,表示自变量 X i X_i Xi 与其他自变量存在较强的相关性,可能存在多重共线性问题。
如果 VIF ( X i ) = 1 \text{VIF}(X_i) = 1 VIF(Xi)=1,表示自变量 X i X_i Xi 与其他自变量之间没有相关性。
如果 VIF ( X i ) < 1 \text{VIF}(X_i) < 1 VIF(Xi)<1,表示自变量 X i X_i Xi 与其他自变量之间存在负相关性。
通常,VIF值大于5或10被认为是多重共线性的警戒线。当VIF值超过这个阈值时,需要进一步分析和处理多重共线性问题。
其中 R 2 R^2 R2的计算逻辑:
-
总平方和(Total Sum of Squares, SST):
S S T = ∑ i = 1 n ( y i − y ˉ ) 2 SST = \sum_{i=1}^{n} (y_i - \bar{y})^2 SST=i=1∑n(yi−yˉ)2 -
残差平方和(Residual Sum of Squares, SSR):
S S R = ∑ i = 1 n ( y i − y ^ i ) 2 SSR = \sum_{i=1}^{n} (y_i - \hat{y}_i)^2 SSR=i=1∑n(yi−y^i)2 -
回归平方和(Regression Sum of Squares, SSR):
S S R = ∑ i = 1 n ( y ^ i − y ˉ ) 2 SSR = \sum_{i=1}^{n} (\hat{y}_i - \bar{y})^2 SSR=i=1∑n(y^i−yˉ)2 -
R 2 R^2 R2 计算:
R 2 = 1 − S S R ( R e s i d u a l ) S S T = 1 − ∑ i = 1 n ( y i − y ^ i ) 2 ∑ i = 1 n ( y i − y ˉ ) 2 R^2 = 1 - \frac{SSR(Residual)}{SST}=1- \frac{ \sum_{i=1}^{n} (y_i - \hat{y}_i)^2}{\sum_{i=1}^{n} (y_i - \bar{y})^2} R2=1−SSTSSR(Residual)=1−∑i=1n(yi−yˉ)2∑i=1n(yi−y^i)2
通过计算每个自变量的VIF值,我们可以获得关于模型中变量间相关性的信息,从而识别和解决多重共线性问题。
R方=1:最理想情况,所有的预测值等于真值。
R方=0:一种可能情况是"简单预测所有y值等于y平均值",即所有 y^i 都等于y¯(即真实y值的平均数),但也有其他可能。
R方<0:模型预测能力差,比"简单预测所有y值等于y平均值"的效果还差。这表示可能用了错误模型,或者模型假设不合理。
R方的最小值没有下限,因为预测可以任意程度的差。因此,R方的范围是 (−∞,1] 。
注意:R方并不是某个数的平方,因此可以是负值。
-
R 2 R^2 R2 与相关系数的关系:
R 2 R^2 R2 是与相关系数直接相关的。对于简单线性回归(只有一个自变量和一个因变量), R 2 R^2 R2与相关系数 r 2 r^2 r2是等价的:
R 2 = r 2 R^2 = r^2 R2=r2 -
方差与 R 2 R^2 R2 的关系:
在多元线性回归中, R 2 R^2 R2可以理解为回归模型解释的方差比例,即因变量 y y y的总方差中能够被模型解释的部分。 R 2 R^2 R2 可以通过下面的公式计算:
R 2 = 1 − 残差平方和 总方差 R^2 = 1 - \frac{\text{残差平方和}}{\text{总方差}} R2=1−总方差残差平方和
其中,总方差等于因变量 y y y 的样本方差。
总的来说, R 2 R^2 R2 表示模型能够解释的方差比例,与相关系数直接相关,但与方差没有直接的数学关系。