数据结构 | 第十二章：优先级队列 | 堆 | 左高树 | 堆排序 | 霍夫曼编码

12.1 定义和应用

优先级队列（priority queue）是0个或多个元素的集合，每个元素都有一个优先级或值。

• 与FIFO队列（先入先出）不同：优先级队列中元素出队列的顺序由元素的优先级决定

• 最小优先级队列：“查找/删除”操作用来“查找/删除”优先级最小的元素。

• 最大优先级队列：“查找/删除”操作用来“查找/删除”优先级最大的元素。

• 优先级队列中的元素可以有相同的优先级。

12.2 抽象数据类型

ADT

抽象数据类型MaxPriorityOueue
{
	实例
		有限个元素集合，每个元素都有一个优先级
	操作
		empty():判断优先级队列是否为空，为空时返回true 
        Size():返回队列中的元素数目
        top():返回优先级最大的元素
        pop():删除优先级最大的元素
        push(x):插入元素x 
}

抽象类

class maxPriorityQueue 
{
    public:
		virtual ~maxPriorityQueue(){}
    	//判断优先级队列是否为空，为空时返回true
    	virtual bool empty()const = 0;
    	//返回队列中的元素数目
 		virtual int size()const = 0;
    	//返回优先级最大的元素
    	virtual const T& top() = 0;
    	//删除优先级最大的元素
    	virtual void pop() = 0;
		//插入元素theElement
		virtual void push(const T& theElement) = 0;
};

优先级队列的描述：线性表、堆、左高树

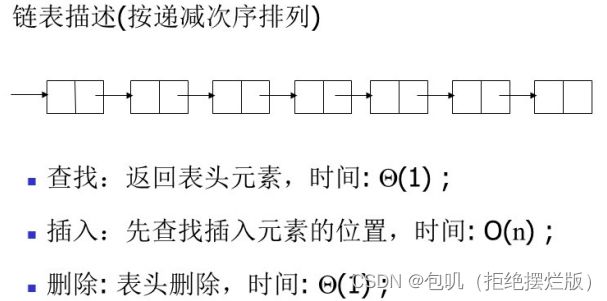
12.3 线性表

采用无序线性表描述最大优先级队列

• 

• 

采用有序线性表描述最大优先级队列

• 

• 

12.4 堆

定义

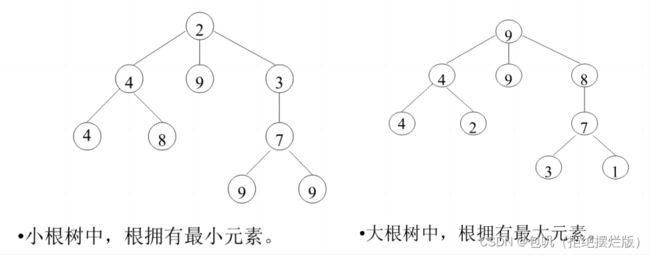
大根树(小根树)：每个节点的值都大于(小于)或等于其子节点(如果有的话)值的树。

大根树或小根树节点的子节点个数可以大于2

大根堆(小根堆)：既是大根树(小根树)，又是完全二叉树

操作(图解＋代码)

小根堆的定义及实现

template<class T>
class minHeap
{
	public:
    	minHeap(int initialCapacity = 10)
		{//构造 
    		arrayLength = initialCapacity + 1;
    		heap = new T[arrayLength];
    		heapSize = 0;
		}
    	~minHeap() { delete[] heap; }//析构 
    	const T& top()
    	{//返回优先级最大的元素的引用 
    		return heap[1];
    	}
    	void pop();//删除
		void push(const T&theElement);//插入
    	void initialize(T*theHeap, int theSize);//初始化 
    	void output(ostream& out) const;//输出 
	private:
		T* heap;//一个类型为T的一维数组 
		int arrayLength;//数组heap的容量 
    	int heapSize;//堆的元素个数               
};

数组长度变换函数

//将一个一维数组的长度从oldLength变成newLength。（后续push操作会用到） 
template<class T>
void changeLengthID(T*& array, int oldLength, int newLength)
{
    //函数首先分配一个新的、长度为newLength的数组
    T* newarray = new T[newLength]; 
    //取min {oldLength, newLength} 
    int number = (oldLength < newLength) ? oldLength : newLength; 
    for (int i = 0; i < number; i++)
        //然后把原数组的前min {oldLength, newLength} 个元素复制到新数组中
		newarray[i] = array[i];
    //释放原数组所占用的空间  
    delete[] array;  
    //将新数组赋值到旧数组完成更改
    array = newarray; 
}

小根堆的插入

新增元素首先插入在堆的末尾元素，然后依据小根堆的性质，自底向上，递归调整。 这里以小根堆为例，大根堆同理；设大根堆的元素个数是n

思路总结

• 将新元素插入到编号为n+1的位置

• 从n+1号位置开始，沿着从该位置到根的路径，判断新元素能否放在该位置（当前判断位置）

  • 能，新元素放入，结束

  • 不能，将父节点上的元素下移到该位置，当前判断位置上移到父节点，继续判断

template<class T>
void minHeap<T>::push(const T& theElement)
{//把元素theElement加入堆
    
	//必要时增加数组长度 
	if (heapSize == arrayLength - 1)
    {//数组长度加倍 
        changeLengthID(heap, arrayLength, 2 * arrayLength);
        arrayLength *= 2;
    }
    
	//为元素theElement寻找插入位置 
	//小根堆要求老叶子比新叶子小 
    int currentNode = ++heapSize;//currentNode从新叶子向上移动，就从最底下开始 
    while (currentNode != 1 && heap[currentNode / 2] > theElement)
    {//这个时候老叶子比新叶子大，不能把元素放在这 
        //把大的那个元素赋给currentNode，相当于把大的元素往下移 
        heap[currentNode] = heap[currentNode / 2]; 
        //同时把currentNode（一个打算插入theElement的位置）移向双亲，就往上移
        currentNode /= 2;                    
    }
    //循环结束，即找到合适的位置插入 
    heap[currentNode] = theElement;
}

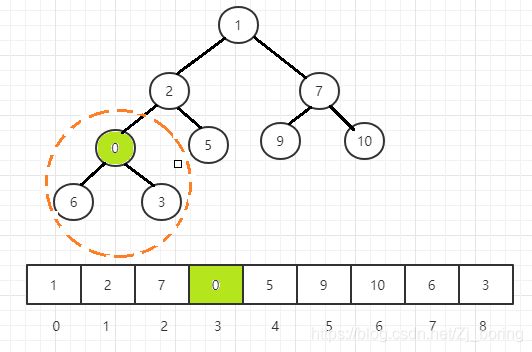
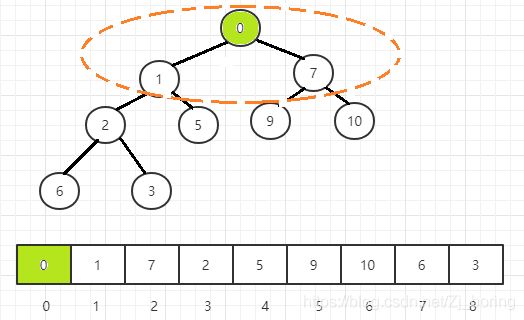
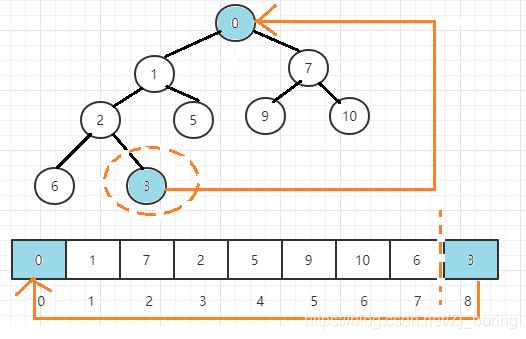
图解——以上面构建的小根堆为例，新插入元素0。

1. 首先在堆的末尾插入新增元素
   

2. 自底向上，递归调整其父节点

小根堆的删除

对于最大堆和最小堆，删除操作是针对堆顶元素而言的，即把末尾元素移动到堆顶，再自定向下(重复构建堆的操作)，递归调整。

思路总结

• 删除堆顶元素，并把末尾元素移动到堆顶

• 从根开始，沿着从根到叶子节点的路径，为移到堆顶的末尾元素寻找合适的位置

• 判断可以把lastElement放入当前位置吗？

  • 可以，lastElement放入，结束

  • 不可以，将当前位置的大孩子上移一层，当前位置下移一层，继续判断

template<class T> 
void minHeap<T>::pop()
{
	//删除堆顶元素
    heap[1].~T(); 
	//删除最后一个元素，然后重新建堆（这一步相当于把末尾元素拿出来） 
    T lastElement = heap[heapSize--];
	//开始给拿出来的末尾元素找合适的放入位置，从顶开始，自顶向下调整 
    int currentNode = 1,
        child = 2;//currentNode的孩子    
    while (child <= heapSize)
    {
    	//heap[child]应该是currentNode的更大的孩子（就是说它的值太大了，应该往后头放） 
        if (child < heapSize && heap[child] > heap[child + 1])
            child++;
		
		//可以把lastElement放在heap[currentNode]吗？ 
		//可以 
        if (lastElement <= heap[child])
            break; 
		//不可以（以下操作和上述push相关操作同理） 
        heap[currentNode] = heap[child];//把孩子child向上移动 
        currentNode = child;//向下移动一层寻找位置          
        child *= 2;
    }
    heap[currentNode] = lastElement;
}

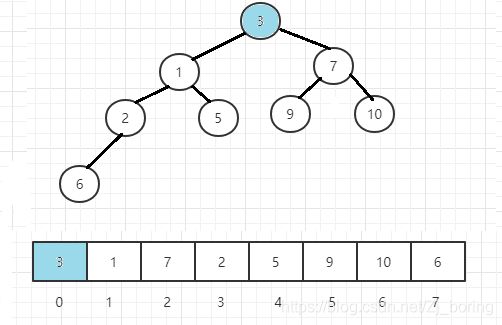
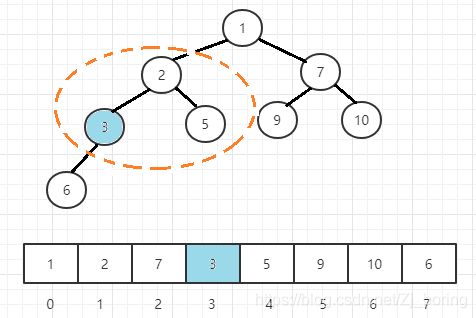
图解

小根堆的初始化

从最右一个有孩子的节点开始调整（root = heapSize / 2，heapSize是最底下，/2相当于往上一层），根据小根堆的性质，越小的数据往上移动

template<class T>
void minHeap<T>::initialize(T* theHeap, int theSize)
{//在数组theHeap[1:theSize]中建小根堆
    delete[] heap;
    heap = theHeap;
    heapSize = theSize;
	
	//堆化 
    for (int root = heapSize / 2; root >= 1; root--)
    {
        T rootElement = heap[root];

        int child = 2 * root; 
        while (child <= heapSize)
        {	
        	//heap[child]应该是兄弟中的较小者 
            if (child < heapSize && heap[child] > heap[child + 1])
                child++;
                
			//可以把rootElement放在heap[child / 2]吗? 
			//可以
            if (rootElement <= heap[child])
                break;  
            //不可以 
            heap[child / 2] = heap[child]; 
            child *= 2;                   
        }
        heap[child / 2] = rootElement;
    }
}

初始化这一部分原理和删除的依次比较流程一样，区别就是

• 删除是从上往下调整，从currentNode = 1, child = 2开始

• 而建堆是从root = heapSize / 2，child = 2 * root开始，凭root--循环向上调整的

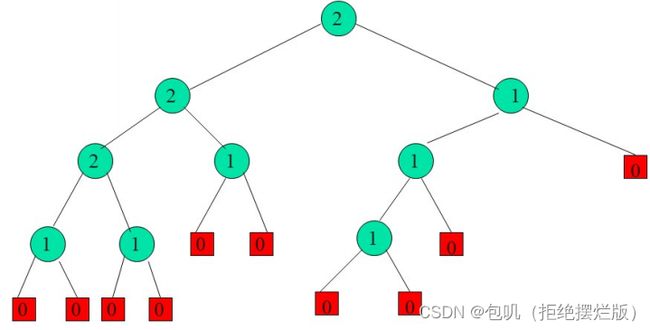
大根堆同理，以下是大根堆初始化的流程示例

12.5 左高树

定义

• 堆结构是一种隐式数据结构，时间效率和空间利用率都很高。

• 左高树是一种适合于实现优先队列的链表结构，可用于合并两个优先队列或多个长度不同的队列

扩充二叉树

• 外部节点——代替树中的空子树的节点

• 内部节点——具有非空子树的节点

• 扩充二叉树——增加了外部节点的二叉树

高度优先左高树(HBLT)

对补充二叉树中的任意节点x，令s(x)为从节点x到它子树的外部节点的所有路径中，最短的一条路径长度

根据s(x)的定义可知：

• 若x是外部节点，则s(x) = 0

• 否则，s(x) = min{s(L),s(R)} + 1，其中L和R分别为x的左右孩子。

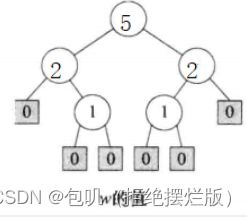
• 当且仅当一棵二叉树的任何一个内部节点，其左孩子的s值大于等于右孩子的s值时，该二叉树称为高度优先左高树。

• 定理：令x为HBLT的一个内部节点，则有：

  • 以x为根的子树的节点数目至少为$2^{s(x)}-1$
  • 若以x为根的子树有m个内部节点，那么s(x)最多为$lo{g}_2(m+1)$
  • 从x到一外部节点的最右路径（即从x开始沿右孩子移动的路径）的长度为s(x)

• 最大(小)HBLT：该二叉树为高度优先左高树同时又是最大(小)树

重量优先左高树(WBLT)

定义x的重量w(x)，为以x为根的子树的内部节点数目

• 若x是外部节点，则w(x) = 0
• 若x为内部节点，其重量为其孩子节点的重量之和加1

• 当且仅当其任何一个内部节点的左孩子的w值大于或等于右孩子的w值，称为重量优先左高树。
• 最大(小)WBIT：该二叉树为重量优先左高树同时又是最大(小)树

操作

以下都以最大HBLT为例，其他同理

类maxHblt

template<typename T>
class maxHblt : public maxPriorityQueue<T>,
				public linkedBinaryTree<pair<int,T>>
{
    public:
        //当队列为空返回true;否则返回false            
        bool empty()const;
        //返回队列的元素个数
        int size()const;
        //返回优先级最大的元素的引用
        const T& top();
		//删除队首元素
        void pop();   
        //插入元素theElement
        void push(const T& theElement);
        //清空树
        void erase(); 
        //初始化一个HBLT
        void initialize(T* theElement, int theSize);
        //将本棵HBLT与参数所指的HBLT进行合并，内部调用私有方法meld
        void meld(maxHblt<T>& theHblt); 
    private:
        void clearTree(binaryTreeNode<pair<int, T>>* t);
        void meld(binaryTreeNode<pair<int,T>>* &x, 		
                  binaryTreeNode<pair<int,T>>*& y);
    private:
        binaryTreeNode<pair<int,T>>* root; //根节点
        int treeSize;//树的大小
};

pair:

• first：节点的s值
• second：优先级队列元素

最大HBLT的插入

最大HBLT的插入操作可利用最大HBLT的合并操作来实现

• 假设元素x要插入名为H的最大HBLT中
• 先建立一棵新的只包含x元素的HBLT
• 然后将这棵新的HBLT与名为H的HBLT进行合并
• 合并之后的HBLT就为插入之后最终的HBLT

template<typename T>
void maxHblt<T>::push(const T& theElement)
{
	//创建一个新节点
	binaryTreeNode<pair<int, T>> *q = 
		new binaryTreeNode<pair<int, T>>(pair<int,T>(1, theElement));
 
	//将新节点与本HBLT进行合并
	this->meld(this->root,q);
	this->treeSize++;
}

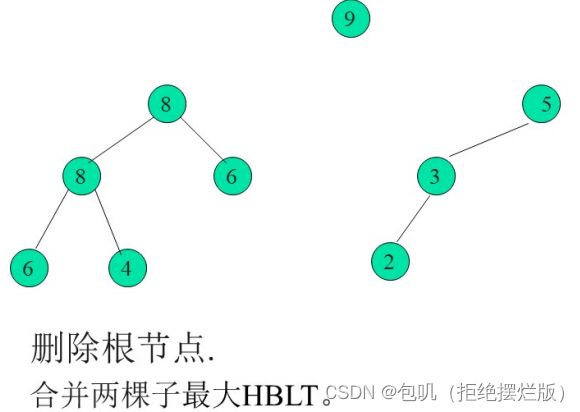
最大HBLT的删除

最大HBLT与大根堆一样，最大元素在根中，因此删除操作也是删除根节点
删除操作也是利用最大HBLT的合并操作来实现

• 若根被删除，则分别以根节点的左右孩子节点为根的子树是两棵最大HBLT
• 然后将这棵最大HBLT合并，之后便是删除后的结果

template<typename T>
void maxHblt<T>::pop()
{
	//如果HBLT为空，不能出队列
	if (this->treeSize == 0)
		throw queueEmpty();
 
	//得到根节点的左右子节点
	binaryTreeNode<pair<int, T>>* left = this->root->leftChild,
		*right=this->root->rightChild;
 
	//删除根节点，将左子节点变为新根节点，然后进行合并
	delete this->root;
	this->root = left;
	meld(this->root, right);
	this->treeSize--;
}

两棵HBLT的合并

A、B：需要合并的两棵最大HBLT。

• 如果一者为空，则另一个便是合并的结果；

• 如果两者均不为空，则进行以下步骤

  • 先比较两个HBLT的根，较大者的根作为合并后的HBLT的根
  • 假设A的根大于B，且A的左子树为AL
  • 然后将A的右子树AR与B合并，然后形成一棵名为C的HBLT（如果A没有右子树，那B就什么都不做）
  • 然后将C与A合并
    • 结果为：以A的根为根，AL与C为左右子树的最大HBLT
    • 如果AL的s值小于C的s值，则以C为左子树，AL为右子树；否则，AL为左子树，C为右子树

• 合并的策略需要使用递归来实现

演示案例

//合并两棵根分别为*x和*y的左高树
template<typename T>
void maxHblt<T>::meld(binaryTreeNode<pair<int, T>>* &x, 
                      binaryTreeNode<pair<int, T>>* &y)
{
	//如果y为空，不进行合并
	if (y == NULL)
		return;
	//如果x为空，那么就将y赋值给x
	if (x == NULL)
	{
		x = y;
		return;
	}
 	//x和y均不为空
	//如果x的值小于y的值，进行交换
	if (x->element.second < y->element.second)
		swap(x, y);
	//将x的右子节点与y合并。如果x没有右子节点，那么就将y设置为x的右子节点
	meld(x->rightChild, y);
	//如果x的左子节点为空，将右子节点设置为左子节点
	if (x->leftChild == NULL) 
    {
		x->leftChild = x->rightChild;
		x->rightChild = NULL;
		//因为把右子节点赋值给左子节点了，所以右子节点为空，那么本节点的s值就为1
		x->element.first = 1;
	}
    //如果左子节点不为空，比较是否需要交换
	else 
	{
		//如果左子节点的s值比右子节点的小，那么就进行交换
		if (x->leftChild->element.first < x->rightChild->element.first) 
        {
			swap(x->leftChild, x->rightChild);
		}
		//因为右子节点到外部节点之间的s值是最小的，所以就将x的s值设置为右子节点的s值+1
		x->element.first = x->rightChild->element.first + 1;
	}
}

最大HBLT的初始化

初始化过程是将n个元素逐个插入最初为空的最大HBLT

• 创建n个仅包含一个元素的最大HBLT，将这n棵树组成一个FIFO队列

• 从队列中依次删除两个最大HBLT，将其合并，再插入队列末尾

• 重复第2步直到队列只有一棵HBLT

演示案例：元素 7,1,9,11,2

template<typename T>
void maxHblt<T>::initialize(T* theElement, int theSize)
{
	//创建一个队列，用来初始化HBLT
	queue<binaryTreeNode<pair<int, T>>*> q;
	//清空当前HBLT
	erase();
 
	//先建立一组HBLT，每个HBLT中只有一个节点
	for (int i = 1; i <=theSize; ++i)
		q.push(new binaryTreeNode<pair<int, T>>(pair<int, T>(1,theElement[i])));
 
	//theSize个HBLT，需要合并theSize-1次
	for (int i = 1; i <= theSize - 1; ++i)
	{
		//从队列中取出两个HBLT进行合并
		binaryTreeNode<pair<int, T>>* b = q.front();
		q.pop();
		binaryTreeNode<pair<int, T>>* c = q.front();
		q.pop();
		//合并
		meld(b, c);
		//合并之后再次放入到队列中
		q.push(b);
	}
	if (theSize > 0)
		this->root = q.front();
	this->treeSize = theSize;
}

补充erase、clearTree函数

template<typename T>
void maxHblt<T>::erase()
{
	//调用clearTree
	clearTree(this->root);
	this->root = NULL;
	this->treeSize = 0;
}
 
template<typename T>
void maxHblt<T>::clearTree(binaryTreeNode<pair<int, T>>* t)
{
	//后序遍历删除
	if (t)
	{
		clearTree(t->leftChild);
		clearTree(t->rightChild);
		delete t;
	}
}

12.6 应用

12.6.1 堆排序

• 将要排序的n个元素初始化为一个大（小）根堆
• 每次从堆中提取（即删除）元素。
  • 如果使用大根堆，各元素将按递增次序提取。
  • 如果使用小根堆，各元素将按递减次序提取。

流程示例

12.6.3 霍夫曼编码

霍夫曼原理理解视频

霍夫曼编码使用补充二叉树进行编码，详见实验10.2

构建霍夫曼树

• 初始化二叉树集合，每个二叉树含一个外部节点，每个外部节点代表字符串中一个不同的字符
• 从集合中选择两棵具有最小权值的二叉树，并把它们合并成一棵新的二叉树。
  • 合并方法是把这两棵二叉树分别作为左右子树
  • 然后增加一个新的根节点，新二叉树的权值为两棵子树权值之和。
• 重复第2步，直到仅剩下一棵树为止。