动态规划(DP)及相关经典问题讲解
前言
动态规划(DP)是计算机编程算法中非常重要的一个知识点,无论是校招 社招,面试官也经常喜欢出此类的编程题来考察面试者的编程能力, 这篇博客主要是概述一下dp的主要思想 然后重点归纳一下动态规划相关经典问题的讲解。
DP基础知识
DP简单可以总结为“一个模型三个特征”。
- “一个模型”是指动态规划适合解决的问题的模型,也就是多阶段决策最优解模型(这个模型同时也是回溯 贪心解决问题的模型)。一般用动态规划解决最优问题时,解决问题需要经历多个决策阶段。每个决策阶段都对应着一组状态。然后我们寻找一组决策序列,经过这组决策序列,能够产生最后在那个期望求解的最优值。
- “三个特征”指的是:最优子结构、无后效性和重复子问题。

牢记,dp问题最重要的核心写出状态转移方程
状态转移方程法的思路:找最优子结构——写状态转移方程——将状态转移方程翻译成代码
上面的知识归纳 读者可以看看后 留个印象,下面我们来看看具体的习题。
经典习题
杨辉三角的最短路径问题
求解 从第一层走到最后一层的最短路径长度是多少
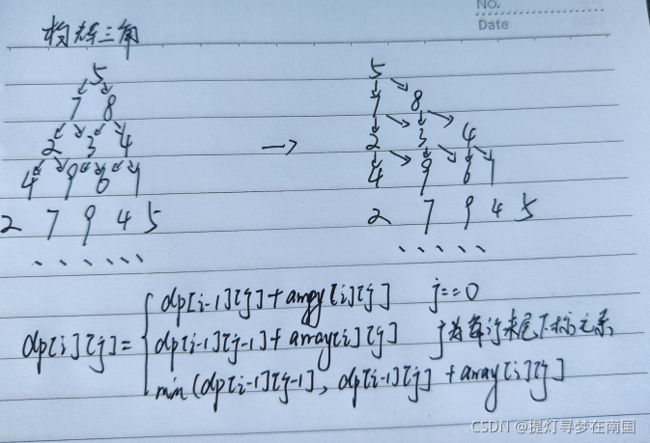
如上面左图所示,也就是我们常见的杨辉三角结构, 在计算机的存储表示中 他的形式如同上面右图所示。每一个节点的运动方向在图中显示, 根据节点数值的运动方向,我们可以比较清晰的概括出该问题的dp状态转换方程dp[i][j]。
代码如下:
public int shortestPath(int[][] array) {
//首先定义一个二维的状态转换数组 中间的值存储的是当前走过的路径
int[][] dp = new int[array.length][array[array.length - 1].length];
dp[0][0] = array[0][0];
//DP的过程如下: 画图便能得到
// 第一列元素对应的状态值只会是运动方向向下得到的 states[i][0]=states[i-1][0]+tri[i][0]
//中间位置的states[i][j] 可以由[i-1][j-1]和[i-1][j]较小的值得到
// 每一行的最后一个元素[i][j]由[i-1][j-1]得到
for (int i = 1; i < array.length; i++) {
for (int j = 0; j < array[i].length; j++) {
if (j == 0) dp[i][j] = dp[i - 1][j] + array[i][j];
else if (j == array[i].length - 1) dp[i][j] = dp[i - 1][j - 1] + array[i][j];
else dp[i][j] = Math.min(dp[i - 1][j - 1], dp[i - 1][j]) + array[i][j];
}
}
//输出最小值 也就是二维数组中最后一行中的最小值
int min = Integer.MAX_VALUE;
for (int j = 0; j < dp[array.length - 1].length; j++) {
min = Math.min(min, dp[array.length - 1][j]);
}
return min;
}
左上到右下的最短路径
一个二维数组中,每个节点的运动方向只能是向下或者向右。求解从左上到右下的最短路径:

因为和上一题杨辉三角的最短路径相似,这里不再进行过多赘述。 dp状态转换方程如图所示。
public int shortestPath(int[][] a) {
int n = a.length, m = a[0].length;
int[][] states = new int[n][m]; 定义状态转换数组
//开始写DP过程
//大多数位置的值states[i][j] 由min(states[i-1][j],states[i][j-1])得到
//第一行只能往右移动 第一列只能向下移动
states[0][0] = a[0][0];
for (int i = 1; i < m; i++) {
states[0][i] = states[0][i - 1] + a[0][i]; //第一行
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < m; j++) {
if (j == 0) states[i][j] = states[i - 1][j] + a[i][j]; //第一列
else {
states[i][j] = Math.min(states[i - 1][j], states[i][j - 1]) + a[i][j];
}
}
}
//输出结果
return states[n - 1][m - 1];
}
代码时间复杂度为O(nm) 空间复杂度为O(nm)
通过观察状态转换方程,还可以通过递归简化代码。递推公式:min_dist(i,j)=a[i][j]+min(min_dist(i-1,j),min_dist(i,j-1))
public int shortestPath2(int[][] a) {
int n = a.length, m = a[0].length;
int[][] states = new int[n][m]; 定义状态转换数组
return recursion(n - 1, m - 1, states, a);
}
public int recursion(int i, int j, int[][] states, int[][] a) { //从states[n-1][m-1]开始调用
if (i == 0 && j == 0) return a[i][j]; //递归终止条件
if (states[i][j] > 0) return states[i][j];
int minLeft = Integer.MAX_VALUE;
if (j - 1 >= 0) {
//非第一列 states[i][j]可以由states[i][j-1]得到
minLeft = recursion(i, j - 1, states, a);
}
int minUp = Integer.MAX_VALUE;
if (i - 1 >= 0) {
//非第一行 states[i][j]可以由states[i-1][j]得到
minUp = recursion(i - 1, j, states, a);
}
states[i][j] = a[i][j] + Math.min(minLeft, minUp);
return states[i][j];
}
左上到右下有多少中走法
在一个二维数组中,元素值1表示可走,元素值为0表示石头 不可通过,请问从左上到右下一共有多少条路径可以到达。
public int countPath(int[][] a) {
int n = a.length, m = a[0].length;
//首先定义一个状态转换表
int[][] state = new int[n][m];
//第一行只能向右走 走法为1
for (int i = 0; i < m; i++) {
state[0][i] = a[0][i];
}
for (int i = 1; i < n; i++) {
for (int j = 0; j < m; j++) {
//第一列都是1 只能向下得到
if (j == 0) state[i][j] = a[i][j];
else {
//这里需要对里面是不是石头进行判断
if (a[i][j] == 0) state[i][j] = 0;
else state[i][j] = state[i - 1][j] + state[i][j - 1]; //递推公式
}
}
}
return state[n - 1][m - 1];
}
0-1背包问题
0-1背包问题1 考虑物品的重量 和背包所承受的最大重量
背包能承受的最大重量为w,有一组数据weight表示每个物品的重量,求解该背包最大装载物品的重量是多少?
例如 w=9,weight=[2, 2, 4, 6, 3]。我们把整个求解过程分为n个阶段,每个阶段来决策一个商品是否装进背包, 每个物品决策完之后 背包剩余承载的最大重量会发生变化, 也就是达到不同的状态 对应到的递归树中有不同的节点。细看,你有没有发现 这就是一个多阶段决策最优解模型。 01背包问题也的确是dp 最经典的问题。

转换为代码如下:
public int DPSlove(int[] weight, int w) {
int n = weight.length;
boolean[][] state = new boolean[n][w + 1]; //定义状态转换表 二维数组)
state[0][0] = state[0][weight[0]] = true;
//利用动态规划状态转移
for (int i = 1; i < n; i++) {
for (int j = 0; j <= w; j++) {
//不把第i个物品放入背包 因为这个下标的重量状态已经存在了
if (state[i - 1][j]) state[i][j] = true;
}
for (int j = 0; j <= w - weight[i]; j++) {
//把第i个物品放入背包
if (state[i - 1][j]) state[i][j + weight[i]] = true;
}
}
//输出结果
for (int i = w; i >= 0; i--) {
if (state[n - 1][i] == true) return i;
}
return 0;
}
时间复杂度为O(nw) 空间复杂度为O(nw)
观察上述代码 for循环中不把第i个商品放入背包的判断可以不用,最后的输出结果也只会和dp数组的最后一行数组相关,因而我们可做下面代码优化:
- dp数组改为一位数组,降低空间消耗
- 0 1背包问题可简化成为只需要靠靠v当前物品是否放入背包
/**
* 在这个函数中 我们对上面的DP过程 做空间上的优化
* 这里只需要采用大小为w+1的一维数组
*/
public int DPSlove2(int[] weight, int w) {
int n = weight.length;
boolean[] states = new boolean[w + 1];
states[0] = states[weight[0]] = true;
for (int i = 1; i < n; i++) {
//DP过程
for (int j = w - weight[i]; j >= 0; j--) {
//这里j需要从大到小进行处理 如果是j从小到大的话,会出现for循环重复计算的问题
//把第i个物品放入背包
if (states[j]) states[j + weight[i]] = true;
}
}
for (int i = w; i >= 0; i--) {
//输出结果
if (states[i]) return i;
}
return 0;
}
0-1 背包问题2 考虑 背包最大承载的重量,每个物品的重量和价值
对比上一个习题,
int w = 9, n = 5;
int[] weight = {2, 2, 4, 6, 3};
int[] value = {3, 4, 8, 9, 6};
之前是 state[][] 存放的是boolean 类型数据 表示该元素放与不放,这里改为当前背包中所装物品的价值总和即可。
public int[] DPSlove(int[] weight, int[] value, int n, int w) {
int[][] state = new int[n][w + 1]; //定义状态转换表 二维数组
state[0][0] = 0;
state[0][weight[0]] = value[0];
//利用动态规划状态转移
for (int i = 1; i < n; i++) {
for (int j = 0; j <= w; j++) {
//不把第i个物品放入背包 因为这个下标的重量状态已经存在了
if (state[i - 1][j] >= 0) state[i][j] = state[i - 1][j];
}
for (int j = 0; j <= w - weight[i]; j++) {
//把第i个物品放入背包
if (state[i - 1][j] >= 0) {
int v = state[i - 1][j] + value[i];
//状态转换数组中 总是保存当前状态对应的最大总价值
if (v > state[i][j + weight[i]]) state[i][j + weight[i]] = v;
}
}
}
//输出结果
int maxValue = -1, maxpos = -1;
for (int j = 0; j <= w; j++) {
if (state[n - 1][j] > maxValue) {
maxValue = state[n - 1][j];
maxpos = j;
}
}
return new int[]{maxpos, maxValue};
}
同样的 也可以对上述代码做一些优化
/**
* 同样是对上面那个DP方法的空间做优化
* 同理 这里的状态转换数组用的是一维数组
*/
public int[] DPSlove2(int[] weight, int[] value, int n, int w) {
int[] states = new int[w + 1]; //定义以为状态转换数组
//同样需要对第一个物品做处理
states[0] = 0;
states[weight[0]] = value[0];
for (int i = 1; i < n; i++) { // dp
for (int j = w - weight[i]; j >= 0; j--) {
//第i个物品放入背包
//把第i个物品放入背包
if (states[j] >= 0) {
int v = states[j] + value[i];
//状态转换数组中 总是保存当前状态对应的最大总价值
if (v > states[j + weight[i]]) states[j + weight[i]] = v;
}
}
}
//输出结果
int maxValue = -1, maxpos = -1;
for (int i = w; i >= 0; i--) {
if (states[i] > maxValue) {
maxValue = states[i];
maxpos = i;
}
}
return new int[]{maxpos, maxValue};
}
两个字符串之间的最长公共子串
给定两个字符串,求解这两个字符串的最长公共子序列(Longest Common Sequence)。比如字符串1:BDCABA;字符串2:ABCBDAB 则这两个字符串的最长公共子序列长度为4,最长公共子序列是:BCBA
dp状态转换方程为

代码如下:
public int lcs(char[] a, char[] b) {
int n = a.length, m = b.length;
int[][] dp = new int[n + 1][m + 1];
for (int i = 1; i <= n; i++) { //这里要注意是<= 不是<
for (int j = 1; j <= m; j++) {
if (a[i - 1] == b[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
else dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
}
}
return dp[n][m];
}
一组数字中的最长递增子序列的长度
例如: 2,9,3,6,5,1,7 的最长递增子序列的长度为4(2,3,(6)5,7)
从题意得知,当前下标 a[i]的最大递增子序列是 之前所有比他小的元素中上升子序列长度最大的加1。
因而状态转换方程为 dp[i] =max(dp[j])+1 if a[i]>a[j] && i>j
public int longestLenDP(int[] a) {
int n = a.length;
int[] dp = new int[n];
Arrays.fill(dp, 1);
int max = 1;
for (int i = 1; i < n; i++) {
for (int j = 0; j < i; j++) {
if (a[j] < a[i]) dp[i] = Math.max(dp[i], dp[j] + 1);
}
max = Math.max(max, dp[i]);
}
return max;
}
股票交易相关问题
股票交易问题是leetcode 经典的dp求解问题了,有如下金典问题:
这里推荐leetcode上 总结归纳比较好的一篇文章 股票问题系列通解(转载翻译) ,强烈建议阅读到这里的读者多看看, 对于动态规划理解和代码优化 会有很大帮助。
结束语
该篇博客前前后后花了几个小时,终于写完了。结合自己的笔记和刷过的题 总结得到了该篇博客 本打算对于股票交易问题做一个叙述 但感觉这篇博客篇幅已经够长 而且网上已有大神总结很不错的文章 这里就不再细细展开了。文章中 如有错误之处 还请留言反馈。