Hashmap源码详解

在开发中的对于数据结构如何选，我们要知道各个数据结构的优缺点：
数组：采用一段连续的存储单元来存储数据。对于指定下标的查找，时间复杂度为O(1)，但在数组中间以及头部插入数据时，需要复制移动后面的元素O(n)。 优点 查找快，缺点插入慢

链表：一种在物理存储单元上非连续、非顺序的存储结构，数据元素的逻辑顺序是通过链表中的指针链接次序实现的。

链表由一系列结点（链表中每一个元素）组成，结点可以在运行时动态生成。每个结点都包含“存储数据单元的数据域”和“存储下一个结点地址的指针域”这两个部分。

由于链表不用必须按顺序存储，所以链表在插入的时候可以达到O(1)的复杂度，但查找一个结点或者访问特定编号的结点需要O(n)的时间。 优点是插入快，缺点查询慢。
而hashmap采用了数组+链表的结构，链表后面又优化为性能更好的红黑树。它的优势是平衡了链表和数组的优缺点。
小总结一下，看你的数据，如果全都是查询，那你就用数组，如果你全都是插入删除就用链表，如果你有插入删除，也有查询就用hashmap。根据实际情况，把握好度。
下面我们来看一下Hashmap源码，看看它是怎么实现的，目的就是为了更好的使用它。

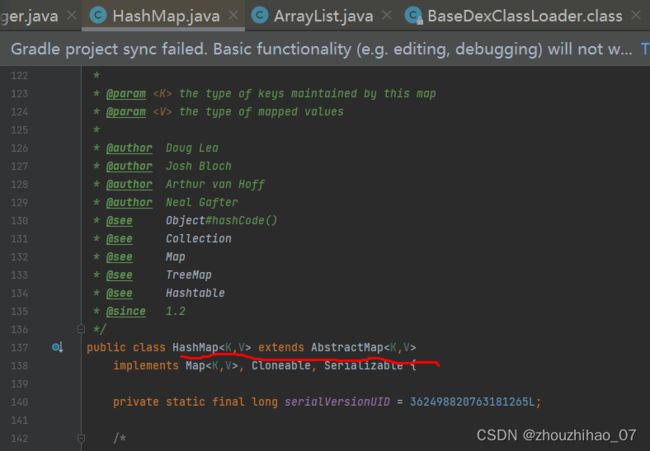
看下图，它是继承了AbstractMap并且实现了Map接口，同时要注意它实现了Cloneable, Serializable接口，是可复制和序列化的数据结构。

AbstractMap是一个抽象类，并且实现了Map接口

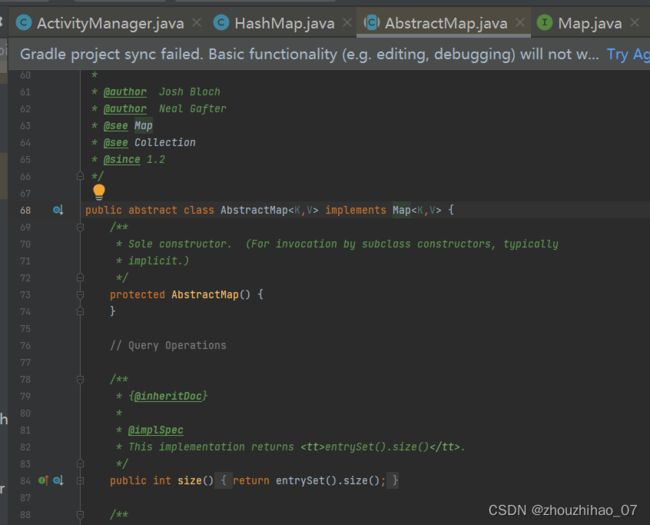
下图中是Map接口里面的一些函数。

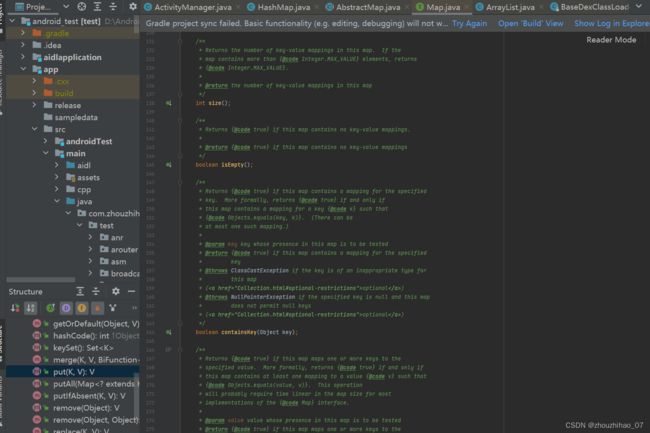
我们从它的put方法入手吧，调用了putVal函数

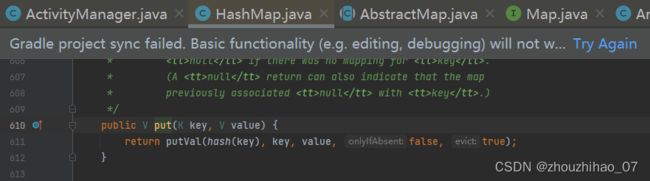
下图就是putVal函数，代码量不少，先看一下Node 是节点吧，注意它的结构 ，有hash值，key，value 还有next 下一个节点。

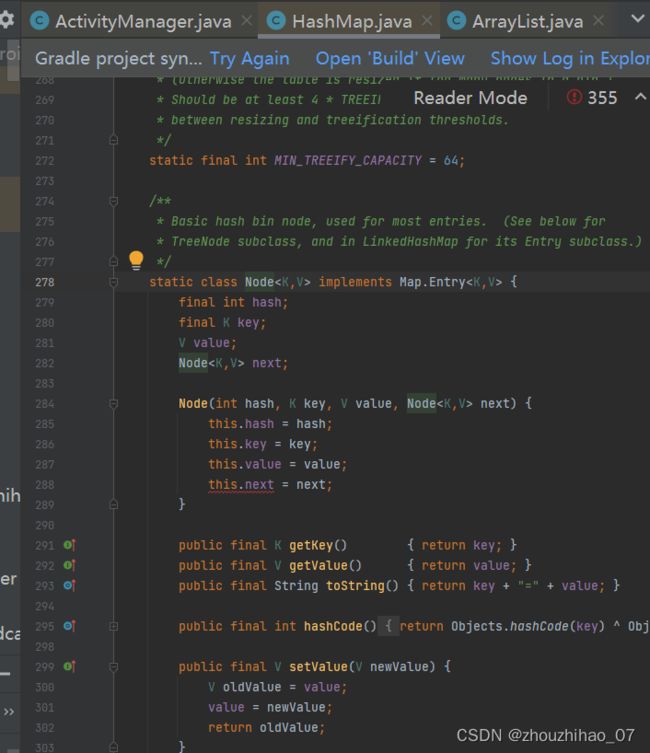
接着putVal函数的逻辑走，注释里面写了逻辑，table就是前面所说的Hashmap里面的数组，item就是链表的节点Node，还有一个数组下标用 index = (n - 1) & hash 来计算的原因，因为n是table的长度，是2^N,所以 这里的（n-1）就是11111，这样的，那么（n-1）&hash就是取hash的后N位，这样的下标index一定小于2^N ,不会下标数组越界。还有一个细节，采用了懒加载在第一次put的时候 resize中进行初始化的

final V putVal(int hash, K key, V value, boolean onlyIfAbsent,
                   boolean evict) {
        Node<K,V>[] tab; Node<K,V> p; int n, i;
        if ((tab = table) == null || (n = tab.length) == 0)
//1、判断当table为null或者tab的长度为0时，即table尚未初始化，此时通过resize()方法得到初始化的table
            n = (tab = resize()).length;
        if ((p = tab[i = (n - 1) & hash]) == null)
//1.1、此处通过（n - 1） & hash 计算出的值作为tab的下标i，并另p表示tab[i]，也就是该链表第一个节点的位置。并判断p是否为null
            tab[i] = newNode(hash, key, value, null);
//1.1.1、当p为null时，表明tab[i]上没有任何元素，那么接下来就new第一个Node节点，调用newNode方法返回新节点赋值给tab[i]
        else {
//2.1下面进入p不为null的情况，有三种情况：p为链表节点；p为红黑树节点；p是链表节点但长度为临界长度TREEIFY_THRESHOLD，再插入任何元素就要变成红黑树了。
            Node<K,V> e; K k;
            if (p.hash == hash &&
                ((k = p.key) == key || (key != null && key.equals(k))))
//2.1.1HashMap中判断key相同的条件是key的hash相同，并且符合equals方法。这里判断了p.key是否和插入的key相等，如果相等，则将p的引用赋给e，这就说明了key是独一无二的，相同的key会被覆盖。

                e = p;
            else if (p instanceof TreeNode)
//2.1.2现在开始了第一种情况，p是红黑树节点，那么肯定插入后仍然是红黑树节点，所以我们直接强制转型p后调用TreeNode.putTreeVal方法，返回的引用赋给e
                e = ((TreeNode<K,V>)p).putTreeVal(this, tab, hash, key, value);
            else {
//2.1.3接下里就是p为链表节点的情形，也就是上述说的另外两类情况：插入后还是链表/插入后转红黑树。另外，上行转型代码也说明了TreeNode是Node的一个子类
                for (int binCount = 0; ; ++binCount) {
//我们需要一个计数器来计算当前链表的元素个数，并遍历链表，binCount就是这个计数器

                    if ((e = p.next) == null) {
                        p.next = newNode(hash, key, value, null);
                        if (binCount >= TREEIFY_THRESHOLD - 1) 
// 插入成功后，要判断是否需要转换为红黑树，因为插入后链表长度加1，而binCount并不包含新节点，所以判断时要将临界阈值减1
                            treeifyBin(tab, hash);
//当新长度满足转换条件时，调用treeifyBin方法，将该链表转换为红黑树
                        break;
                    }
                    if (e.hash == hash &&
                        ((k = e.key) == key || (key != null && key.equals(k))))
                        break;
                    p = e;
                }
            }
            if (e != null) { // existing mapping for key
                V oldValue = e.value;
                if (!onlyIfAbsent || oldValue == null)
                    e.value = value;
                afterNodeAccess(e);
                return oldValue;
            }
        }
        ++modCount;
        if (++size > threshold)
            resize();
        afterNodeInsertion(evict);
        return null;
    }

下图是由链表转换成树结构的逻辑方法：

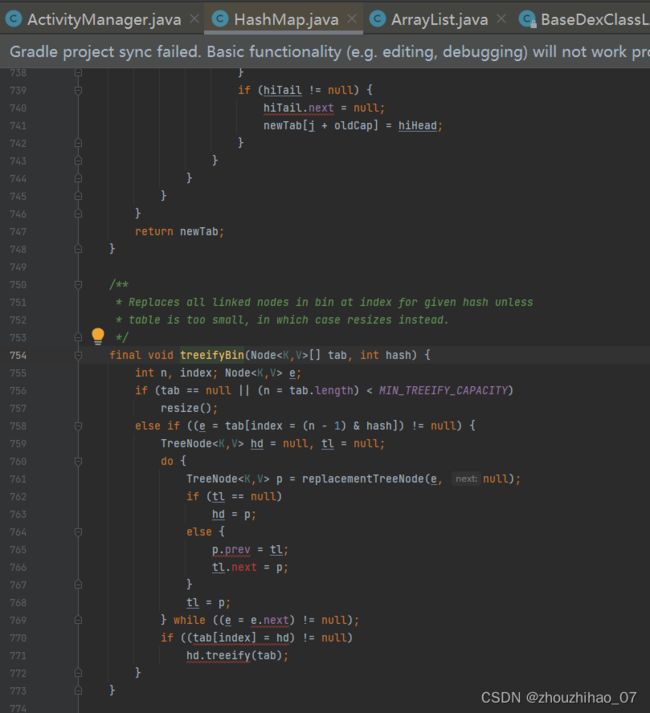
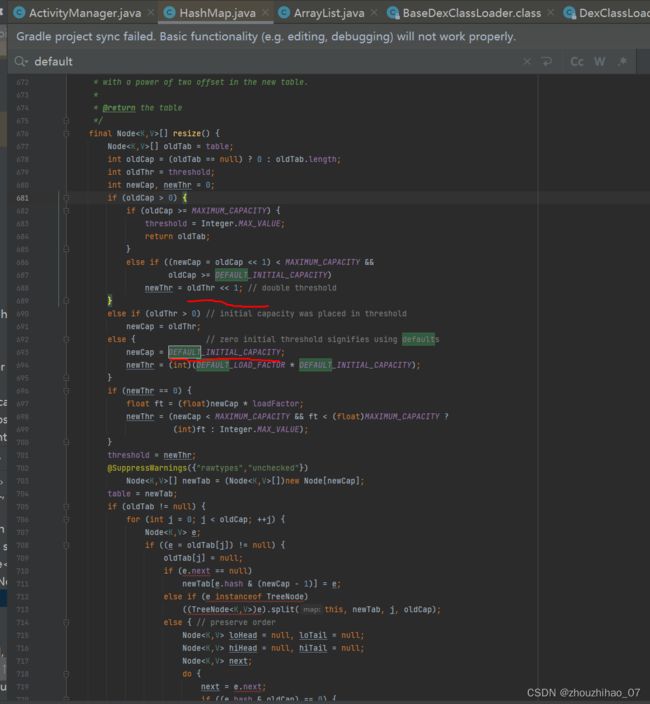
还有一个重要的函数resize（），当需要扩容的时候是左移一位就是旧的长度的2倍，初始值就是DEFAULT_INITIAL_CAPACITY=1<<4也就是16， 负载因子 DEFAULT_LOAD_FACTOR = 0.75f ，当长度达到了 newCap * loadFactor 原来长度的0.75倍 这个限制的时候就会触发resize扩容，负载因子和初始数组大小都是可以设置的，这在我们使用hashmap的时候，根据自己实际需要控制，让它更高效。

它的get方法就比较简单了，通过key 推出hash值，然后由hash值算出数组index 第一个元素，如果key一致就返回，如果不是，再往这个链表或者树上去找，这么看来，hashmap 解决hash冲突的办法是链表寻址法，关于hash冲突的问题我提一点就是：hash函数需要保证一件事情:对于两个相同的输入,产生相同的输出。这里需要强调,并不能保证两个相同的输出对应的是相同的输入。