手撕二叉树oj练习

目录

1、单值二叉树

2、检查两棵树是否相同

3、对称二叉树

4、翻转二叉树

5、二叉树前序遍历

6、二叉树中序遍历

7、二叉树后续遍历

8、另一棵树的子树

9、二叉树的构建及遍历

---

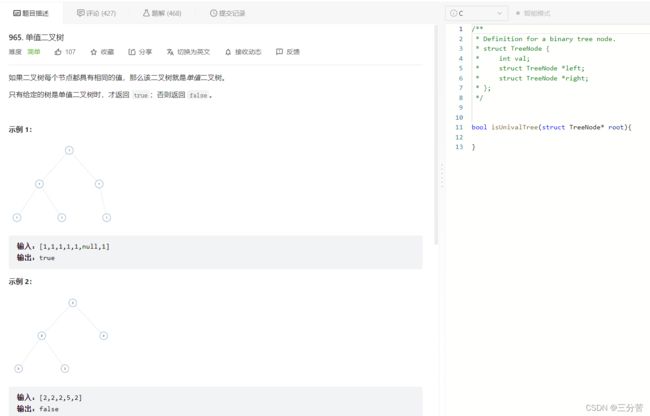
1、单值二叉树

•  链接直达：

单值二叉树

• 题目：

• 思路： 递归 + 分治

单值二叉树，顾名思义，就是说所有节点的值val是相同的，这里我们采用分治的思想。具体操作过程是将每个节点都去和根节点比较，如果存在不等，就返回false。如果每个根和其左右孩子都相等，那么我们就可以断定此二叉树必是单值二叉树，因为根节点也会成为孩子，孩子也会成为根结点。而上述操作均是建立在递归+分治的基础上完成的。

• 代码如下：

bool isUnivalTree(struct TreeNode* root) {
    if (root == NULL)
    {
        return true; //如果为空树，同样符合单值，直接返回true
    }
    if (root->left && root->left->val != root->val)
    {
        return false;//如果左孩子存在并且左孩子和根结点不同，返回false
    }
    if (root->right && root->right->val != root->val)
    {
        return false;//如果右孩子存在并且右孩子和根结点不同，返回false
    }
    return isUnivalTree(root->left) && isUnivalTree(root->right);//递归+分治，转化子问题
}

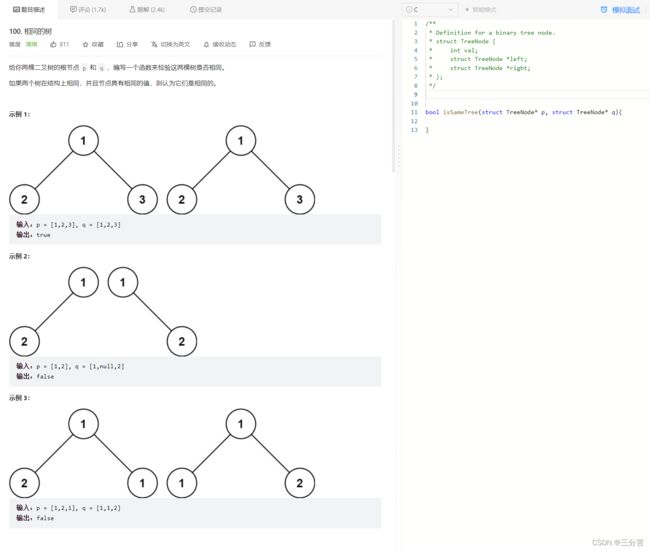
2、检查两棵树是否相同

•  链接直达：

相同的树

• 题目：

• 思路：分治+递归

首先得看清题目需求，两颗相同的树，而不是对称的树，相同的树就说明其对应节点的值val应均相等。要先排除些特殊情况，如若两棵树的根节点均为空，那么符合题意，如若有任何一棵树先为空，那么同样不符合，其次就是判断节点值是否相等，最后就是最基本的递归（递归左子树和右子树）+分治即可解决此问题。

• 代码演示：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    //都是空树
    if (p == NULL & q == NULL)
    {
        return true; //如果p和q均为NULL，成立，返回true
    }
    //一个为空，一个不为空
    if (p == NULL || q == NULL)
    {
        return false; //若p和q其中一个先为空，那么不相同，返回false
    }
    //都不为空
    if (p->val != q->val)
    {
        return false; //如果对应子树的值不同，同样返回false
    }
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);//分治+递归
}

3、对称二叉树

• 链接直达：

对称二叉树

• 题目：

• 思路：递归+分治

细看此题，要看清楚是对称二叉树，也就是说某个节点的左和对称节点的右相等，正如示例1：左子树节点2的左（3）等于右子树节点2的右（3），而2的右等于镜像2的左。此题我们可以再写一个辅助函数，专门判断，对称节点的值是否相等，再在主函数使用递归+分治的思想转换成子问题继续比较其余的节点。

• 代码演示：

 //辅助函数比较对称的值是否相等
bool _isSymmetric(struct TreeNode* p, struct TreeNode* q) {
    if (p == NULL & q == NULL)
    {
        return true; //如果p和q均为NULL，成立，返回true
    }
    if (p == NULL || q == NULL)
    {
        return false; //若p和q其中一个先为空，那么不相同，返回false
    }
    if (p->val != q->val)
    {
        return false; //如果对应子树的值不同，同样返回false
    }
    return _isSymmetric(p->left, q->right) && _isSymmetric(p->right, q->left);//分治+递归
}
bool isSymmetric(struct TreeNode* root) {
    if (root == NULL)
    {
        return true;
    }
    return _isSymmetric(root->left, root->right);
}

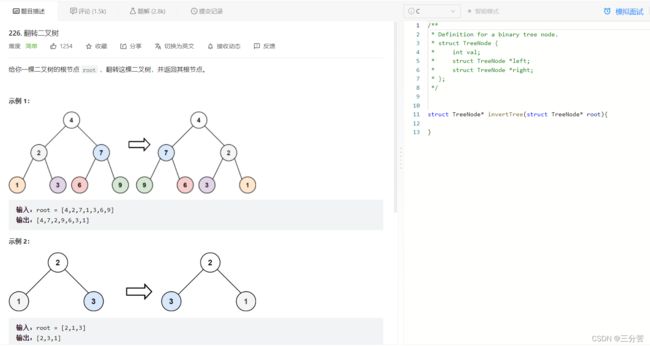
4、翻转二叉树

• 链接直达：

翻转二叉树

• 题目：

• 思路：

此题的思想依旧是递归+分治，老生常谈。可以这样下手：既然是翻转二叉树，那如果说我们可以假设就从根结点开始（根结点不为空）使根结点的左右子树交换，那么不就是解决了第一层和第二层的翻转了嘛，接下来需要达到翻转剩下层数的效果话，可以使用递归将其根结点的左子树传过去作为根结点，并交换左右子树，将根结点的右子树传过去作为新的根结点并交换左右子树……以此类推，当每一个左右子树交换完毕，则翻转完毕。因此，可以额外写一个辅助函数专门进行交换节点，主函数进行递归+分治。

• 代码演示：

//辅助函数，专门交换结点
void SwapNode(struct TreeNode* root)
{
    struct TreeNode* tmp = root->left;
    root->left = root->right;
    root->right = tmp;
}

struct TreeNode* invertTree(struct TreeNode* root) {
    if (root == NULL)
    {
        return NULL;
    }
    SwapNode(root);//交换结点
    invertTree(root->left);
    invertTree(root->right);
    return root;
}

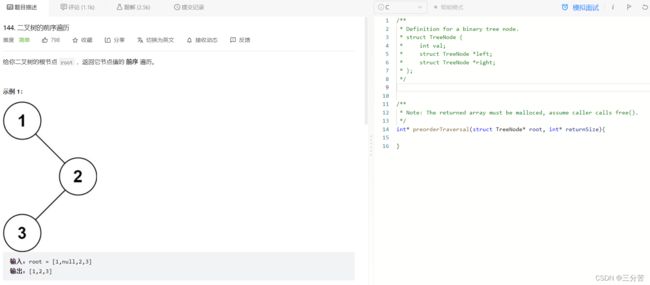
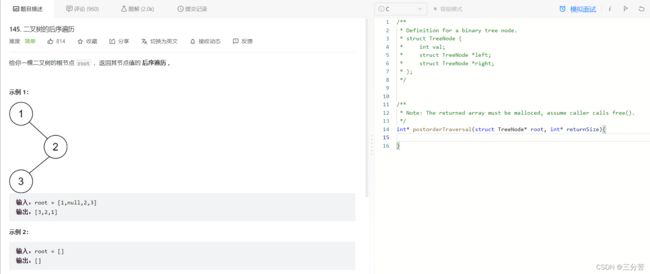
5、二叉树前序遍历

• 链接直达：

二叉树的前序遍历

• 题目：

• 思路：

前序遍历，上篇博文才讲过的遍历方式，此题让我们进行模拟实现，题中明确指出要动态开辟一块数组来存放数据，在开辟之前首先要解决的难题是，要开辟的空间是多大？我们就可以单独写个辅助函数TreeSize来帮助我们计算，求节点个数还是比较简单的，递归+分治即可，跟上篇博文思想一样，开辟数组后，接下来就和我们先前的前序遍历一样，先把数据放数组里头，再递归+分治，不过又出现一个问题，当把递归放到主函数进行时，也就意味着每递归一次都要malloc，不妥，此时再封装一个函数专门进行递归即可。

• 注意：

在我们传节点个数时，记得传地址，因为每次递归都会建立栈帧，递归完即销毁，无法保存，此点在上篇博文专门讲过这个问题，不过多赘述。

此题还有一个*returnSize，这个东西是要返回数组的元素个数，返回给调用者，让他来验证你的结果对不对

• 代码演示：

//写一个辅助函数求出二叉树的节点的个数，方便后续malloc
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

//再写一个辅助函数中专门进行递归，防止用主函数递归时每次都要malloc
void _preorder(struct TreeNode* root, int* a, int* i)
{
    //如果二叉树为空，直接返回
    if (root == NULL)
    {
        return;
    }
    //
    a[(*i)++] = root->val;
    _preorder(root->left, a, i);
    _preorder(root->right, a, i);
}

int* preorderTraversal(struct TreeNode* root, int* returnSize) {
    //用size来接收节点个数
    int size = TreeSize(root);
    //动态开辟数组
    int* a = (int*)malloc(sizeof(int) * size);
    int i = 0;
    //注意i要传地址，因为每次递归都会建立栈帧，递归完即销毁
    _preorder(root, a, &i);
    *returnSize = i;
    return a;
}

6、二叉树中序遍历

• 链接直达：

二叉树的中序遍历

• 题目：

• 思路：

此题和上题近乎一致，唯一的变化只是在赋值数据到数组的位置有所变化，具体过程看代码：

• 代码演示：

//计算树的结点个数，方便后续malloc数组
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//创建辅助函数专门用来递归
void InOrder(struct TreeNode* root, int* a, int* i)
{
    if (root == NULL)
    {
        return;
    }
    InOrder(root->left, a, i);
    a[(*i)++] = root->val;
    InOrder(root->right, a, i);
}
int* inorderTraversal(struct TreeNode* root, int* returnSize) {
    int size = TreeSize(root);
    int* a = (int*)malloc(sizeof(int) * size);
    int i = 0;
    InOrder(root, a, &i);
    *returnSize = i;
    return a;
}

7、二叉树后续遍历

• 链接直达：

二叉树的后续遍历

• 题目：

• 思路：

有了前序，中序遍历的铺垫，后续自然也差不多就可以直接写出来了：

• 代码演示：

//计算结点个数
int TreeSize(struct TreeNode* root)
{
    return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}
//辅助函数专门递归
void PosOrder(struct TreeNode* root, int* a, int* i)
{
    if (root == NULL)
    {
        return;
    }
    PosOrder(root->left, a, i);
    PosOrder(root->right, a, i);
    a[(*i)++] = root->val;
}
int* postorderTraversal(struct TreeNode* root, int* returnSize) {
    int size = TreeSize(root);
    int* a = (int*)malloc(sizeof(int) * size);
    int i = 0;
    PosOrder(root, a, &i);
    *returnSize = i;
    return a;
}

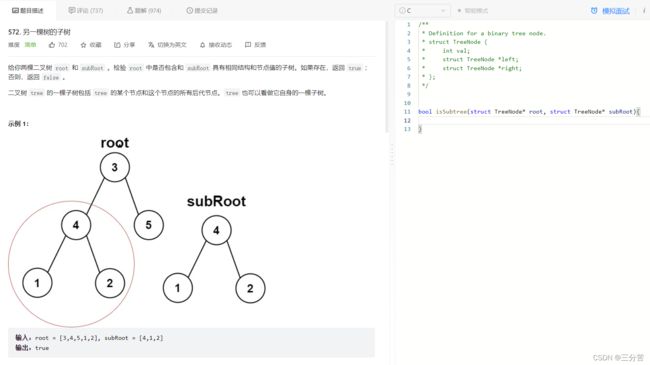
8、另一棵树的子树

• 链接直达：

另一棵树的子树

• 题目：

• 思路：

遍历左边的树的每一个结点，作子树的根，跟右边的子树都比较一下，此时我们就可以单独封装一个先前写过的函数isSameTree，用来比较两棵树是否相同，依次比较，若是子树，返回true

• 代码演示：

//辅助函数，专门判断两棵树是否相同
bool isSameTree(struct TreeNode* root, struct TreeNode* subRoot)
{
    if (root == NULL && subRoot == NULL)
    {
        return true;
    }
    if (root == NULL || subRoot == NULL)
    {
        return false;
    }
    if (root->val != subRoot->val)
    {
        return false;
    }
    return isSameTree(root->left, subRoot->left) && isSameTree(root->right, subRoot->right);
}

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot) {
    if (root == NULL)
    {
        return false; //根都为空了，何来子树，直接返回false
    }
    if (isSameTree(root, subRoot))
    {
        return true; //是子树就返回false
    }
    return isSubtree(root->left, subRoot) || isSubtree(root->right, subRoot);
}

9、二叉树的构建及遍历

• 链接直达：

二叉树的构建及遍历

• 题目：

• 思路：

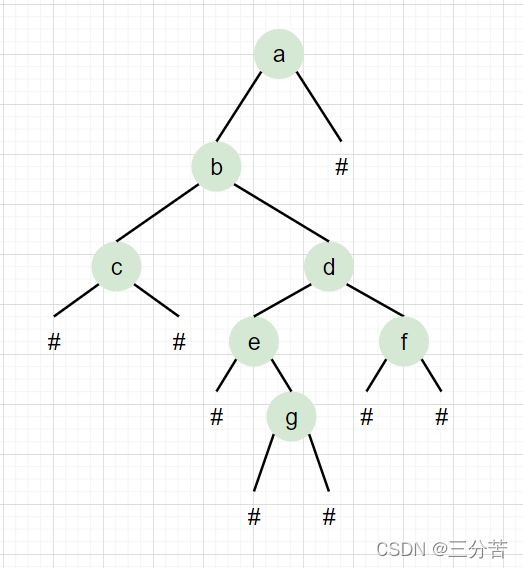
此题明确指出要根据我们输入的字符串将其构建成树，再按照中序的遍历方式输出。以此字符串为例：

• 注意：

题目中还有一个要求，在根据字符串创建树时是按照先序的遍历方式创建的，也就是根->左子树->右子树。如下递归过程：

• 构建树：

首先遇到a，不是#，继续往下构建左子树b，再往下构建左子树c，再递归构建c的左子树为#，也就是空，此时递归c的右子树#为空，递归回来链到b的右子树d，继续构建d的左子树e，构建e的左子树#为空，递归返回构建e的右子树g，再递归g的左右子树均为空，递归返回d的右子树f，构建f的左右子树均为#空，递归返回a的右子树#为空，至此构建树结束，效果如下：

• 中序遍历输出

 当我们创建好二叉树的结构后，只需要将其按照题意中序遍历的方式打印出来即可，而中序遍历已经讲解过，直接递归即可

• 代码演示： 

#include
//创建二叉树结构
typedef struct BinaryTreeNode
{
    char data;
    struct BinaryTreeNode* left;
    struct BinaryTreeNode* right;
}BTNode;
//创捷结点，先序结构创建
BTNode* CreateTree(char* a, int* pi)
{
    if (a[*pi] == '#')
    {
        (*pi)++;
        return NULL;
    }

    BTNode* root = (BTNode*)malloc(sizeof(BTNode));
    root->data = a[(*pi)++];

    root->left = CreateTree(a, pi);
    root->right = CreateTree(a, pi);
    return root;
}

void InOrder(BTNode* root)
{
    if (root == NULL)
        return;
    InOrder(root->left);
    printf("%c ", root->data);
    InOrder(root->right);
}

int main()
{
    char a[100];
    scanf("%s", a);
    int i = 0;
    BTNode* tree = CreateTree(a, &i);
    InOrder(tree);
    return 0;
}