程序员必须掌握的算法系列之搜索算法
一:引言
搜索算法是计算机科学中一类十分重要且常见的算法,它们在各个领域和应用场景中都有广泛的应用。搜索算法可以帮助程序员快速地在大规模的数据中找到目标元素,从而提高程序的效率和准确性。对于一个程序员来说,掌握各种搜索算法是必不可少的,可以帮助他们更好地解决实际问题,提高自己的编程水平。
二:常见搜索算法介绍
在计算机科学中,常见的搜索算法包括线性搜索、二分搜索、广度优先搜索(BFS)和深度优先搜索(DFS)等等。
1. 线性搜索
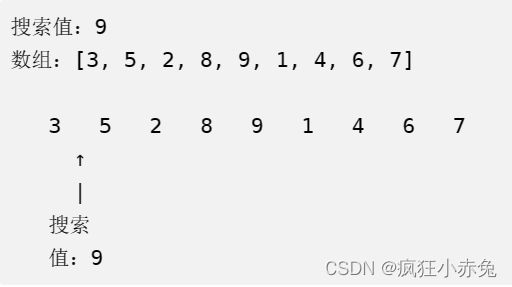
线性搜索是最简单也是最常用的搜索算法之一。它的工作原理是从数据集的起始位置开始逐个检查元素,直到找到目标元素或遍历完整个数据集。线性搜索的时间复杂度为O(n),其中n是数据集中元素的个数。
示例代码(Java):
public class LinearSearch {
public static int linearSearch(int[] arr, int target) {
for (int i = 0; i < arr.length; i++) {
if (arr[i] == target) {
return i;
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {4, 2, 9, 7, 5};
int target = 7;
int index = linearSearch(arr, target);
if (index != -1) {
System.out.println("目标元素在数组中的索引为:" + index);
} else {
System.out.println("目标元素不在数组中");
}
}
}
示例代码(Python):
def linear_search(arr, target):
for i in range(len(arr)):
if arr[i] == target:
return i
return -1
arr = [4, 2, 9, 7, 5]
target = 7
index = linear_search(arr, target)
if index != -1:
print("目标元素在列表中的索引为:", index)
else:
print("目标元素不在列表中")
2. 二分搜索
二分搜索是一种高效的搜索算法,它要求数据集必须有序。它的工作原理是通过比较目标元素和数据集中间元素的大小关系来确定目标元素在左半部分还是右半部分,从而缩小搜索范围。二分搜索的时间复杂度为O(logn),其中n是数据集中元素的个数。如上图的小游戏,就是二分算法应用于生活和娱乐的一种场景。
示例代码(Java):
public class BinarySearch {
public static int binarySearch(int[] arr, int target) {
int left = 0;
int right = arr.length - 1;
while (left <= right) {
int mid = left + (right - left) / 2;
if (arr[mid] == target) {
return mid;
} else if (arr[mid] < target) {
left = mid + 1;
} else {
right = mid - 1;
}
}
return -1;
}
public static void main(String[] args) {
int[] arr = {2, 4, 5, 7, 9};
int target = 7;
int index = binarySearch(arr, target);
if (index != -1) {
System.out.println("目标元素在数组中的索引为:" + index);
} else {
System.out.println("目标元素不在数组中");
}
}
}
示例代码(Python):
def binary_search(arr, target):
left = 0
right = len(arr) - 1
while left <= right:
mid = left + (right - left) // 2
if arr[mid] == target:
return mid
elif arr[mid] < target:
left = mid + 1
else:
right = mid - 1
return -1
arr = [2, 4, 5, 7, 9]
target = 7
index = binary_search(arr, target)
if index != -1:
print("目标元素在列表中的索引为:", index)
else:
print("目标元素不在列表中")
3. 广度优先搜索(BFS)
广度优先搜索是一种图论算法,用于在图或树中寻找某个节点到另一个节点的最短路径。它通过逐级地遍历节点来搜索目标节点,并使用队列来保存待遍历的节点。广度优先搜索的时间复杂度为O(V+E),其中V是节点数,E是边数。
示例代码(Java):
import java.util.*;
public class BreadthFirstSearch {
public static boolean bfs(HashMap<Integer, List<Integer>> graph, int start, int target) {
if (!graph.containsKey(start) || !graph.containsKey(target)) {
return false;
}
Queue<Integer> queue = new LinkedList<>();
HashSet<Integer> visited = new HashSet<>();
queue.offer(start);
visited.add(start);
while (!queue.isEmpty()) {
int node = queue.poll();
if (node == target) {
return true;
}
List<Integer> neighbors = graph.get(node);
for (int neighbor : neighbors) {
if (!visited.contains(neighbor)) {
queue.offer(neighbor);
visited.add(neighbor);
}
}
}
return false;
}
public static void main(String[] args) {
HashMap<Integer, List<Integer>> graph = new HashMap<>();
graph.put(0, Arrays.asList(1, 2));
graph.put(1, Arrays.asList(2));
graph.put(2, Arrays.asList(0, 3));
graph.put(3, Arrays.asList(3));
int start = 2;
int target = 3;
boolean result = bfs(graph, start, target);
if (result) {
System.out.println("从节点" + start + "到节点" + target + "存在路径");
} else {
System.out.println("从节点" + start + "到节点" + target + "不存在路径");
}
}
}
示例代码(Python):
from collections import deque
def bfs(graph, start, target):
if start not in graph or target not in graph:
return False
queue = deque()
visited = set()
queue.append(start)
visited.add(start)
while queue:
node = queue.popleft()
if node == target:
return True
neighbors = graph[node]
for neighbor in neighbors:
if neighbor not in visited:
queue.append(neighbor)
visited.add(neighbor)
return False
graph = {
0: [1, 2],
1: [2],
2: [0, 3],
3: [3]
}
start = 2
target = 3
result = bfs(graph, start, target)
if result:
print("从节点", start, "到节点", target, "存在路径")
else:
print("从节点", start, "到节点", target, "不存在路径")
4. 深度优先搜索(DFS)
深度优先搜索是一种图论算法,用于在图或树中寻找某个节点到另一个节点的路径。它通过递归地遍历节点来搜索目标节点,并使用栈来保存待遍历的节点。深度优先搜索的时间复杂度为O(V+E),其中V是节点数,E是边数。
当我们来到一个迷宫中,希望找到一条从起点到终点的路径。深度优先搜索就像是一个探险家在迷宫中不停地尝试所有可能的路径。我们可以从起点开始,选择一个方向前进。它会一直走到不能再前进为止,然后它会回溯到上一个决策点,换个方向前进,直到无法再走。然后它继续回溯,但这次是回溯到另一个决策点。这个过程将继续下去,直到找到一条从起点到终点的路径。
示例代码(Java):
import java.util.*;
public class DepthFirstSearch {
public static boolean dfs(HashMap<Integer, List<Integer>> graph, int start, int target) {
if (!graph.containsKey(start) || !graph.containsKey(target)) {
return false;
}
Stack<Integer> stack = new Stack<>();
HashSet<Integer> visited = new HashSet<>();
stack.push(start);
visited.add(start);
while (!stack.isEmpty()) {
int node = stack.pop();
if (node == target) {
return true;
}
List<Integer> neighbors = graph.get(node);
for (int neighbor : neighbors) {
if (!visited.contains(neighbor)) {
stack.push(neighbor);
visited.add(neighbor);
}
}
}
return false;
}
public static void main(String[] args) {
HashMap<Integer, List<Integer>> graph = new HashMap<>();
graph.put(0, Arrays.asList(1, 2));
graph.put(1, Arrays.asList(2));
graph.put(2, Arrays.asList(0, 3));
graph.put(3, Arrays.asList(3));
int start = 2;
int target = 3;
boolean result = dfs(graph, start, target);
if (result) {
System.out.println("从节点" + start + "到节点" + target + "存在路径");
} else {
System.out.println("从节点" + start + "到节点" + target + "不存在路径");
}
}
}
示例代码(Python):
def dfs(graph, start, target):
if start not in graph or target not in graph:
return False
stack = []
visited = set()
stack.append(start)
visited.add(start)
while stack:
node = stack.pop()
if node == target:
return True
neighbors = graph[node]
for neighbor in neighbors:
if neighbor not in visited:
stack.append(neighbor)
visited.add(neighbor)
return False
graph = {
0: [1, 2],
1: [2],
2: [0, 3],
3: [3]
}
start = 2
target = 3
result = dfs(graph, start, target)
if result:
print("从节点", start, "到节点", target, "存在路径")
else:
print("从节点", start, "到节点", target, "不存在路径")
三:重点搜索算法总结
搜索算法在计算机科学中有着广泛的应用,常见的搜索算法包括线性搜索、二分搜索、广度优先搜索和深度优先搜索等。这些搜索算法可以帮助程序员解决各种实际问题,提高程序的效率和准确性。
程序员需要掌握搜索算法的种类和知识点,以便在实际开发中能够灵活应用。搜索算法的选择要根据具体的应用场景和数据特点来进行,根据数据的有序性和规模合理选择适合的搜索算法。
在学习搜索算法时,建议程序员多多参考相关的教程、书籍和实践经验,通过代码实现和调试来加深对算法的理解和掌握。同时,也要积极参与算法竞赛和解题训练,锻炼自己的思维和编程能力,提升在实际工作中解决问题的能力。
掌握和深入研究搜索算法对于程序员来说是一项长期的学习和实践过程,但只要保持持续学习和不断实践,相信每个程序员都能够成为搜索算法领域的专家。让我们一起努力,抓住搜索算法这个重要的“必抓!”点,不断提高自己的算法水平!