怒刷LeetCode的第8天(Java版)
目录
第一题
题目来源
题目内容
解决方法
方法一:双指针和排序
编辑第二题
题目来源
题目内容
解决方法
方法一:双指针
方法二:递归
方法三:快慢指针
方法四:栈
第三题
题目来源
题目内容
解决方法
方法一:栈
方法二:字符串替换
方法三:链表
方法四:栈和正则表达式
第一题
题目来源
18. 四数之和 - 力扣(LeetCode)
题目内容
解决方法
方法一:双指针和排序
根据题目要求,可以使用双指针和排序法来解决这个问题。
使用双指针解决四数之和问题的算法思路如下:
1、对数组进行排序,将其从小到大排列。
2、使用两重循环分别枚举前两个数,其中第一个数的下标范围是0到n-4,第二个数的下标范围是第一个数的下标加1到n-3。
4、在两重循环中,使用双指针分别指向当前枚举的两个数之后的位置。
5、每次计算四个数的和,并根据和与目标值的比较结果进行如下操作:
- 如果和等于目标值,将四个数加入答案。
- 如果和小于目标值,将左指针右移一位。
- 如果和大于目标值,将右指针左移一位。
- 同时,如果左指针或右指针指向的数字与上一次迭代的数字相同,继续移动指针直到遇到不同的数字。
6、循环结束后,返回所有符合条件的四个数的组合。
class Solution {
public List> fourSum(int[] nums, int target) {
List> quadruplets = new ArrayList>();
if (nums == null || nums.length < 4) {
return quadruplets;
}
Arrays.sort(nums);
int length = nums.length;
for (int i = 0; i < length - 3; i++) {
if (i > 0 && nums[i] == nums[i - 1]) {
continue;
}
if ((long) nums[i] + nums[i + 1] + nums[i + 2] + nums[i + 3] > target) {
break;
}
if ((long) nums[i] + nums[length - 3] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
for (int j = i + 1; j < length - 2; j++) {
if (j > i + 1 && nums[j] == nums[j - 1]) {
continue;
}
if ((long) nums[i] + nums[j] + nums[j + 1] + nums[j + 2] > target) {
break;
}
if ((long) nums[i] + nums[j] + nums[length - 2] + nums[length - 1] < target) {
continue;
}
int left = j + 1, right = length - 1;
while (left < right) {
long sum = (long) nums[i] + nums[j] + nums[left] + nums[right];
if (sum == target) {
quadruplets.add(Arrays.asList(nums[i], nums[j], nums[left], nums[right]));
while (left < right && nums[left] == nums[left + 1]) {
left++;
}
left++;
while (left < right && nums[right] == nums[right - 1]) {
right--;
}
right--;
} else if (sum < target) {
left++;
} else {
right--;
}
}
}
}
return quadruplets;
}
} 复杂度分析:
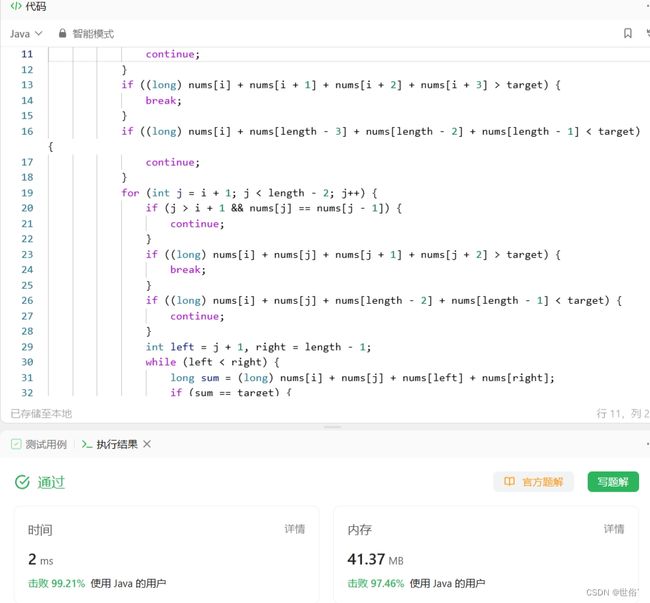
- 时间复杂度为O(n^3),其中n是数组的长度。这是因为代码中有两重循环,加上双指针的遍历,总的时间复杂度为O(n^2)。而在双指针的遍历过程中,左右指针最多各自遍历一次数组,所以时间复杂度为O(n)。
- 空间复杂度方面,代码只使用了常数级别的额外空间,主要是存储结果列表,所以空间复杂度为O(1)。
总结起来,该算法的时间复杂度为O(n^3),空间复杂度为O(1)。需要注意的是,在代码中已经进行了一些剪枝操作,以优化算法的效率。
LeetCode运行结果:
 第二题
第二题
题目来源
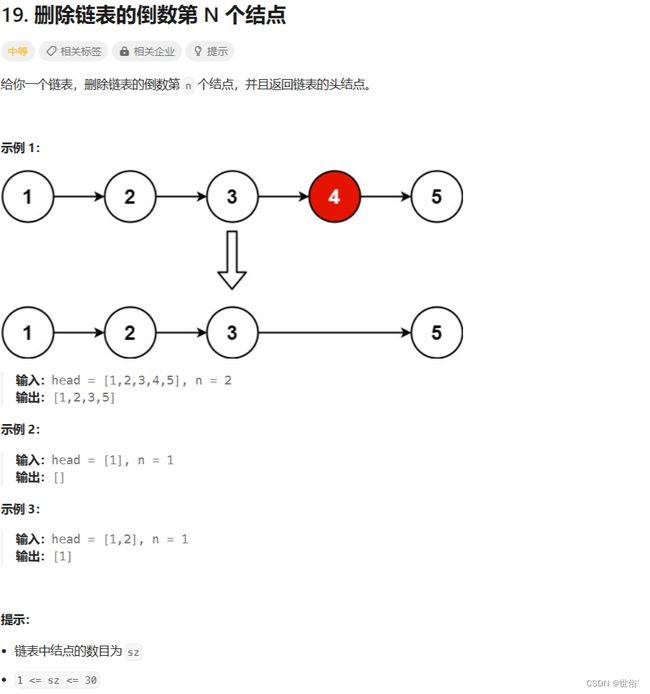
19. 删除链表的倒数第 N 个结点 - 力扣(LeetCode)
题目内容
解决方法
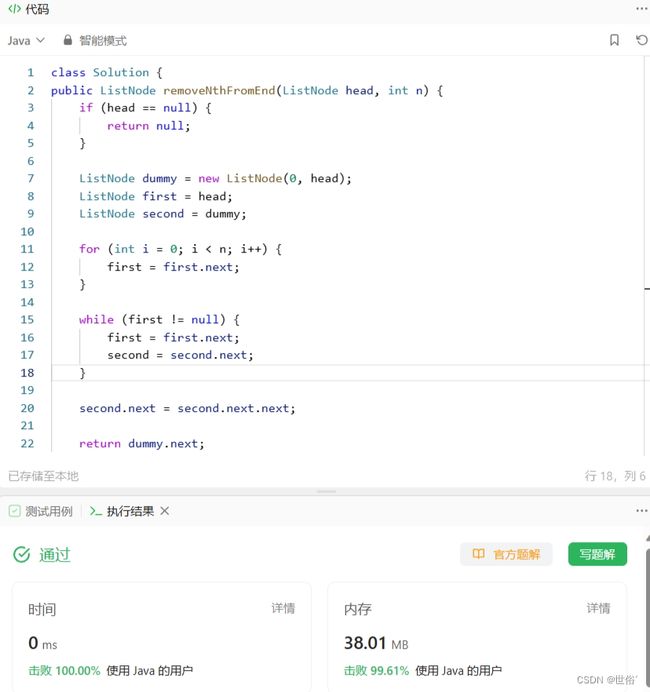
方法一:双指针
这道题可以使用双指针来实现。具体做法是,先让第一个指针往前移动n个位置,然后同时移动第一个指针和第二个指针,直到第一个指针到达链表尾部。此时,第二个指针所指向的节点就是要删除的节点的前一个节点,我们只需要将该节点的next指针指向下一个节点,即可完成删除操作。
需要注意的几点是:
- 要处理删除头结点的情况;
- 链表中可能只有一个节点。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if (head == null) {
return null;
}
ListNode dummy = new ListNode(0, head);
ListNode first = head;
ListNode second = dummy;
for (int i = 0; i < n; i++) {
first = first.next;
}
while (first != null) {
first = first.next;
second = second.next;
}
second.next = second.next.next;
return dummy.next;
}
}复杂度分析:
- 对于给定的链表,我们只需要进行一次遍历即可找到要删除的节点的前一个节点。因此,时间复杂度为O(n),其中n是链表的长度。
- 在空间复杂度方面,我们只使用了常数级别的额外空间,主要是两个指针变量和一个虚拟头节点。因此,空间复杂度为O(1)。
综上所述,该算法的时间复杂度为O(n),空间复杂度为O(1)。
LeetCode运行结果:
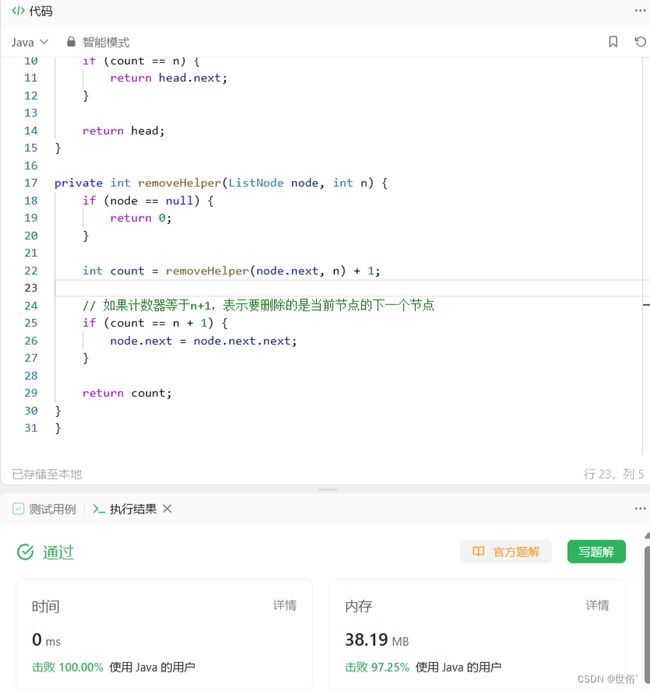
方法二:递归
除了双指针法之外,我们还可以使用递归来解决这个问题。具体做法是,在递归的过程中,使用一个计数器来记录当前遍历到的节点位置,并从链表的末尾开始向前遍历。当计数器等于n时,将当前节点的next指针指向下一个节点的next指针,即完成删除操作。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if (head == null) {
return null;
}
int count = removeHelper(head, n);
// 如果计数器等于n,表示要删除的是头结点
if (count == n) {
return head.next;
}
return head;
}
private int removeHelper(ListNode node, int n) {
if (node == null) {
return 0;
}
int count = removeHelper(node.next, n) + 1;
// 如果计数器等于n+1,表示要删除的是当前节点的下一个节点
if (count == n + 1) {
node.next = node.next.next;
}
return count;
}
}该方法的思路是通过递归实现回溯,每次递归返回当前节点所处的位置。在返回的过程中,不断判断计数器的值是否等于n或n+1,并进行相应的删除操作。
复杂度分析:
- 时间复杂度:在递归过程中,需要遍历整个链表,即O(n)次递归调用。每次递归操作都需要O(1)的时间,因此总体时间复杂度为O(n)。
- 空间复杂度:递归调用会占用栈空间,最坏情况下,递归的深度为链表的长度n,因此空间复杂度为O(n),除去递归栈空间外,不需要额外的空间。
LeetCode运行结果:
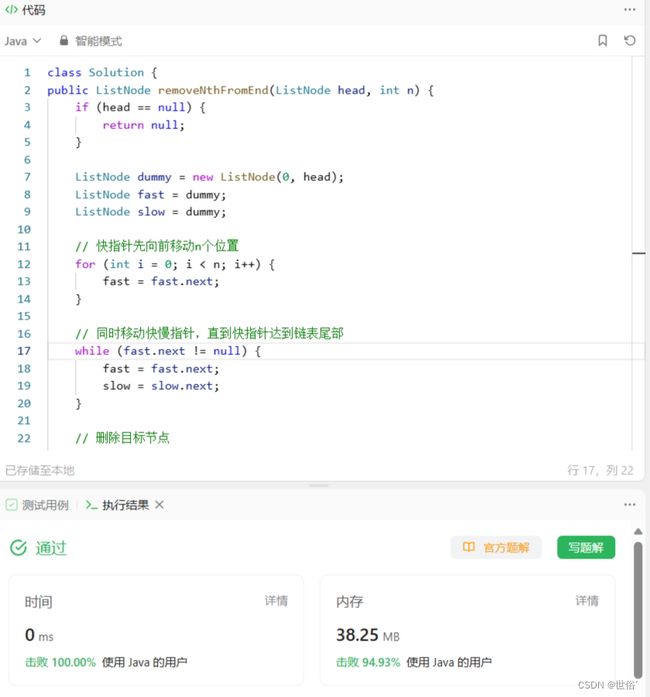
方法三:快慢指针
另一种常见的思路是使用快慢指针。首先,我们让快指针向前移动n个位置。然后,同时移动快指针和慢指针,直到快指针达到链表尾部。此时,慢指针所指的节点就是要删除的节点的前一个节点,我们只需将其next指针指向下一个节点,即可完成删除操作。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if (head == null) {
return null;
}
ListNode dummy = new ListNode(0, head);
ListNode fast = dummy;
ListNode slow = dummy;
// 快指针先向前移动n个位置
for (int i = 0; i < n; i++) {
fast = fast.next;
}
// 同时移动快慢指针,直到快指针达到链表尾部
while (fast.next != null) {
fast = fast.next;
slow = slow.next;
}
// 删除目标节点
slow.next = slow.next.next;
return dummy.next;
}
}该方法的思路是通过快慢指针的差距来定位要删除的节点的前一个节点。快指针先向前移动n个位置,然后同时移动快慢指针,直到快指针到达链表尾部。这样,慢指针所指的节点就是要删除的节点的前一个节点。
复杂度分析:
- 时间复杂度:需要遍历整个链表,除了初始化指针外,只需一次遍历即可完成任务。因此时间复杂度为O(n)。
- 空间复杂度:只使用了常数级别的额外空间,即定义的指针变量,因此空间复杂度为O(1)。
注意:递归解法和快慢指针解法的时间复杂度都是O(n),其中递归解法的空间复杂度为O(n),而快慢指针解法的空间复杂度为O(1)。因此,在大多数情况下,推荐使用快慢指针解法,因为它的空间复杂度更低。
LeetCode运行结果:
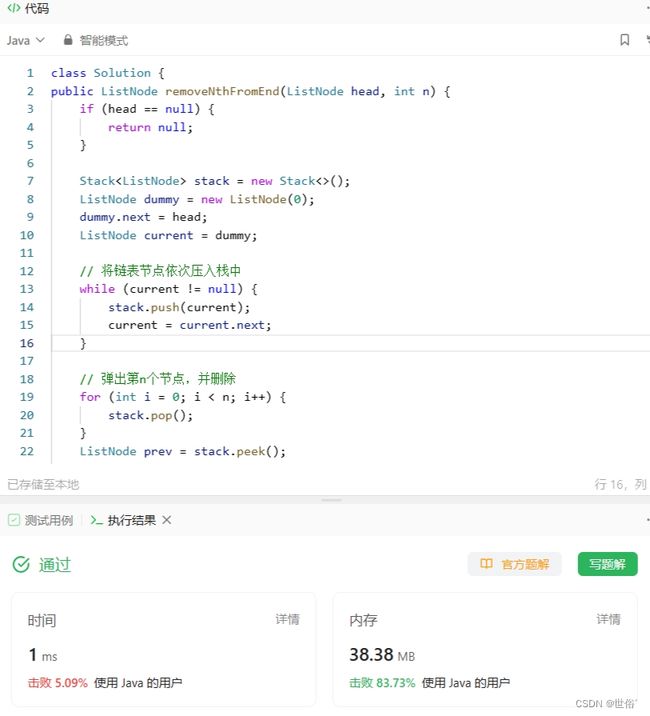
方法四:栈
- 首先,遍历链表并将每个节点都压入栈中。
- 然后,从栈顶开始弹出节点,同时计数。
- 当计数等于n时,表示栈顶节点就是要删除的节点。此时,只需修改相应的指针即可完成删除操作。
class Solution {
public ListNode removeNthFromEnd(ListNode head, int n) {
if (head == null) {
return null;
}
Stack stack = new Stack<>();
ListNode dummy = new ListNode(0);
dummy.next = head;
ListNode current = dummy;
// 将链表节点依次压入栈中
while (current != null) {
stack.push(current);
current = current.next;
}
// 弹出第n个节点,并删除
for (int i = 0; i < n; i++) {
stack.pop();
}
ListNode prev = stack.peek();
prev.next = prev.next.next;
return dummy.next;
}
} 复杂度分析:
- 时间复杂度:遍历链表将节点压入栈中需要O(n)的时间,弹出第n个节点并删除需要O(n)的时间,因此总体时间复杂度为O(n)。
- 空间复杂度:创建了一个栈来存储链表节点,栈的空间消耗取决于链表的长度,所以空间复杂度为O(n)。
综上所述,使用栈解法删除链表中倒数第n个节点的时间复杂度为O(n),空间复杂度为O(n)。相较于快慢指针解法的O(1)的空间复杂度,栈解法的空间复杂度较高。因此,在大多数情况下,推荐使用快慢指针解法。
LeetCode运行结果:
第三题
题目来源
20. 有效的括号 - 力扣(LeetCode)
题目内容
解决方法
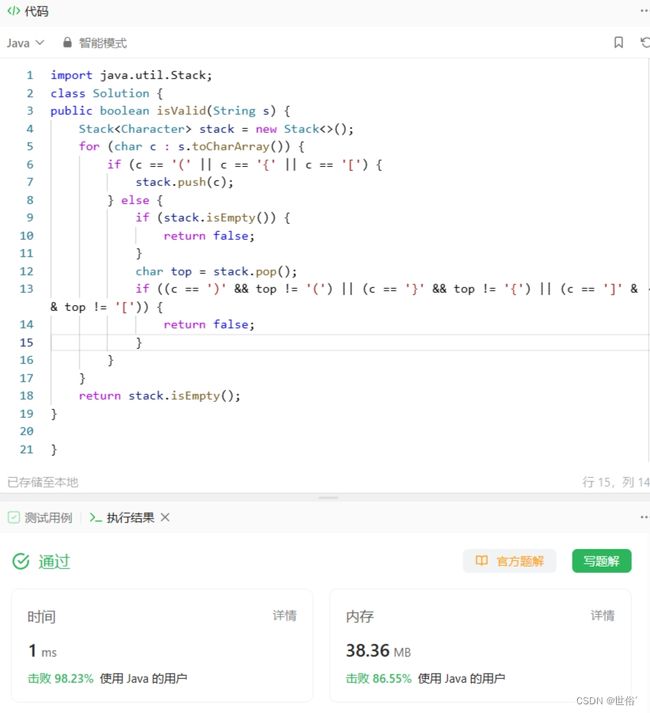
方法一:栈
这个问题可以使用栈来解决。我们可以遍历字符串,当遇到左括号时,将其入栈,当遇到右括号时,判断栈顶元素是否与当前右括号匹配。如果匹配,则将栈顶元素出栈,继续遍历;如果不匹配或栈为空,则说明字符串无效。
import java.util.Stack;
class Solution {
public boolean isValid(String s) {
Stack stack = new Stack<>();
for (char c : s.toCharArray()) {
if (c == '(' || c == '{' || c == '[') { // 遇到左括号,入栈
stack.push(c);
} else if (c == ')' || c == '}' || c == ']') { // 遇到右括号,判断是否匹配
if (stack.isEmpty()) {
return false; // 栈为空,无法匹配
}
char top = stack.pop(); // 弹出栈顶元素
if ((c == ')' && top != '(') ||
(c == '}' && top != '{') ||
(c == ']' && top != '[')) {
return false; // 括号不匹配
}
}
}
return stack.isEmpty(); // 如果栈为空,则所有括号都匹配成功
}
} 复杂度分析:
在遍历字符串时,时间复杂度为O(n),其中n是字符串的长度。同样,使用了一个栈来存储字符,空间复杂度也为O(n)。因此,该解法的时间复杂度和空间复杂度均为O(n)。
LeetCode运行结果:
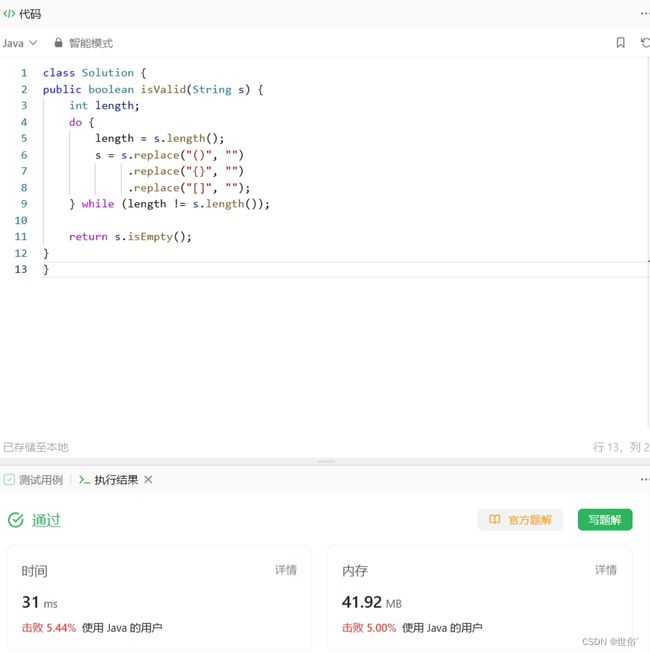
方法二:字符串替换
可以使用字符串替换的方式来判断括号是否匹配。具体思路是:不断替换匹配的括号对"()"、"{}"和"[]"为空字符串,直到字符串中不再包含任何括号对,若最终字符串为空,则说明括号是匹配的。
class Solution {
public boolean isValid(String s) {
int length;
do {
length = s.length();
s = s.replace("()", "")
.replace("{}", "")
.replace("[]", "");
} while (length != s.length());
return s.isEmpty();
}
}复杂度分析:
在每次替换操作后,字符串的长度会减少,因此时间复杂度取决于替换操作的次数。最坏情况下,需要进行n/2次替换,其中n是字符串的长度,因此时间复杂度为O(n^2)。由于每次替换操作都会创建新的字符串,因此空间复杂度为O(n)。
需要注意的是:虽然该方法实现简单,但是对于大规模的输入数据,性能可能不理想。因此,在实际应用中,更常用的是栈方法。
LeetCode运行结果:
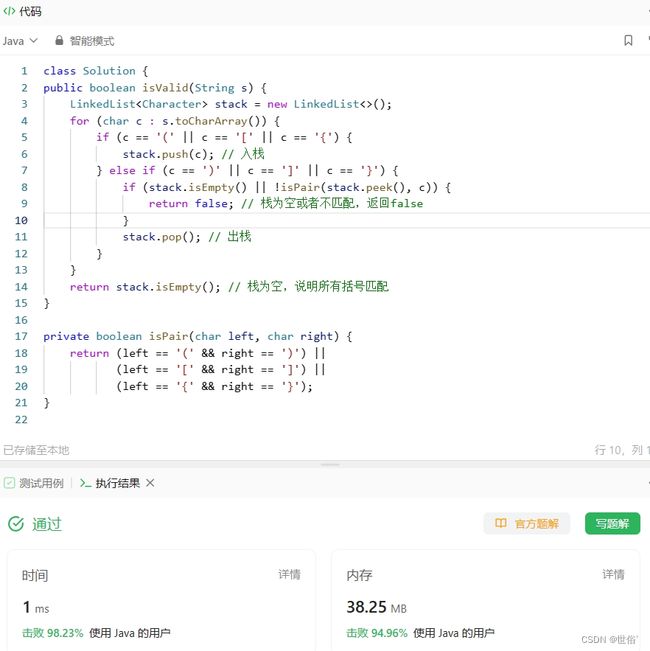
方法三:链表
可以使用链表来模拟栈的操作,从而判断括号是否匹配。具体思路是:遍历字符串,当遇到左括号时,将其入栈(即链表的头部插入节点),当遇到右括号时,判断栈顶节点与当前右括号是否匹配,如果匹配则出栈(即删除链表的头节点),否则返回false。最后,如果栈为空,则说明所有括号都已匹配。
class Solution {
public boolean isValid(String s) {
LinkedList stack = new LinkedList<>();
for (char c : s.toCharArray()) {
if (c == '(' || c == '[' || c == '{') {
stack.push(c); // 入栈
} else if (c == ')' || c == ']' || c == '}') {
if (stack.isEmpty() || !isPair(stack.peek(), c)) {
return false; // 栈为空或者不匹配,返回false
}
stack.pop(); // 出栈
}
}
return stack.isEmpty(); // 栈为空,说明所有括号匹配
}
private boolean isPair(char left, char right) {
return (left == '(' && right == ')') ||
(left == '[' && right == ']') ||
(left == '{' && right == '}');
}
} 复杂度分析:
- 在遍历字符串的过程中,每次入栈、出栈操作的时间复杂度为O(1),因此总体时间复杂度是O(n)。
- 链表的空间复杂度与字符串的长度相关,如果所有的字符都是左括号,那么链表的节点个数就是字符串的长度;如果所有的字符都是右括号,链表为空。因此,空间复杂度是O(n)。
需要注意的是,这种方法使用链表模拟栈,可能会产生额外的空间开销。相比直接使用栈数据结构,链表方式相对繁琐一些,并且在插入和删除节点时,需要更多的时间开销。
LeetCode运行结果:
方法四:栈和正则表达式
import java.util.Stack;
import java.util.regex.Pattern;
import java.util.regex.Matcher;
class Solution {
public static boolean isValid(String s) {
Pattern pattern = Pattern.compile("\\(\\)|\\[\\]|\\{\\}"); // 匹配括号对的模式
Matcher matcher;
Stack stack = new Stack<>();
while (!s.isEmpty()) {
matcher = pattern.matcher(s);
if (matcher.find()) {
s = matcher.replaceAll(""); // 替换匹配到的括号对为空字符串
} else {
char c = s.charAt(0);
if (c == '(' || c == '[' || c == '{') {
stack.push(c); // 左括号入栈
} else if (c == ')' || c == ']' || c == '}') {
if (stack.isEmpty() || !isPair(stack.pop(), c)) {
return false; // 栈为空或者不匹配,返回false
}
}
s = s.substring(1); // 删除已处理的字符
}
}
return stack.isEmpty(); // 栈为空,说明所有括号匹配
}
private static boolean isPair(char left, char right) {
return (left == '(' && right == ')')
|| (left == '[' && right == ']')
|| (left == '{' && right == '}');
}
public static void main(String[] args) {
String s = "(([]){})";
System.out.println(isValid(s)); // 输出 true
}
} 这个方法首先使用正则表达式匹配并替换字符串中的括号对为空字符串,直到字符串中不再包含任何括号对。此后,使用栈来判断剩余的括号是否匹配。最终,如果栈为空,则说明所有括号都已匹配。
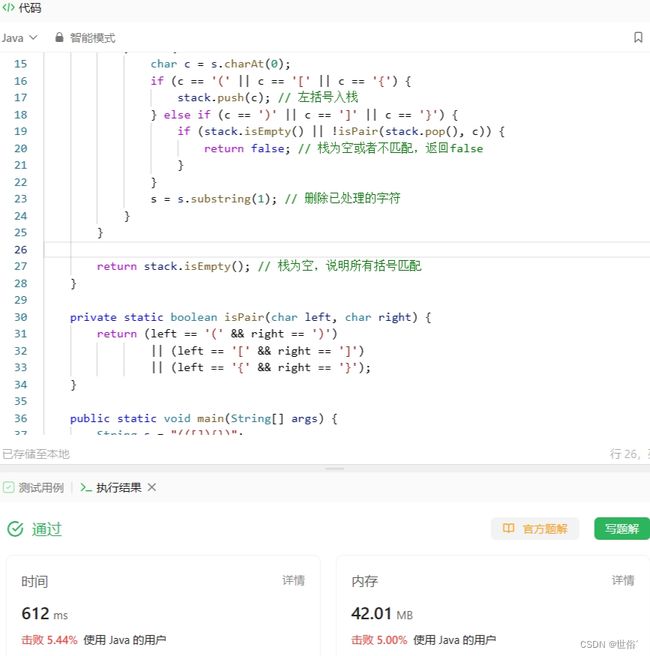
请注意,虽然这个方法利用了正则表达式来部分处理括号对的情况,但它依然使用了栈来判断括号是否匹配。这是因为正则表达式无法处理嵌套较深的括号结构。
复杂度分析:
时间复杂度分析:
- 正则表达式匹配和替换的时间复杂度:在每次循环中,使用正则表达式的
replaceAll方法替换字符串中的括号对。假设字符串长度为n,那么这个操作的时间复杂度是O(n)。 - 循环次数的上界:在最坏情况下,当括号都是成对出现且互相嵌套时,需要执行n/2次循环。因此,循环的时间复杂度是O(n)。
- 栈的操作的时间复杂度:在每次循环中,可能进行一次栈的压入或弹出操作,时间复杂度是O(1)。整个算法执行的过程中,最多进行n/2次栈操作,因此栈的时间复杂度是O(n)。
综上所述,基于正则表达式和栈的方法的总体时间复杂度是O(n)。
空间复杂度分析:
- 正则表达式对象的空间复杂度:创建一个Pattern对象来表示匹配括号对的正则表达式,其空间复杂度是O(1)。
- 栈的空间复杂度:在最坏情况下,当所有的括号都是左括号时,栈的深度是n/2。因此,栈的空间复杂度是O(n)。
- 其他临时变量的空间复杂度:除了栈之外,算法只使用了常数级别的额外空间。因此,其他临时变量的空间复杂度是O(1)。
综上所述,基于正则表达式和栈的方法的总体空间复杂度是O(n)。
需要注意的是:这些复杂度分析是基于最坏情况下的分析结果。在实际应用中,具体的时间复杂度和空间复杂度可能会有所不同,具体取决于输入字符串的特点。
LeetCode运行结果: