代码随想录Day02 数组基础2 leetcode T977有序数组的平方, T209 长度最小的子数组,T59 螺旋矩阵II
本文思路和详细解答来源于:
代码随想录
视频讲解见:
双指针法经典题目 | LeetCode:977.有序数组的平方_哔哩哔哩_bilibili
Leetcode T977 有序数组的平方
题目链接:
977. 有序数组的平方 - 力扣(LeetCode)
思路1: 暴力求解
这里先解释一下非递减顺序:
1223445
非递增顺序:
5443221
首先我们可以使用暴力求解,直接创建一个新数组,将原数组的元素平方放入新数组,再将新数组使用快排,就完成了.
时间复杂度:O(nlogn)
class Solution {
public:
vector sortedSquares(vector& A) {
for (int i = 0; i < A.size(); i++) {
A[i] *= A[i];
}
sort(A.begin(), A.end()); // 快速排序
return A;
}
}; 思路2: 双指针写法
我们发现,平方之后较大的数一定在两边,所以,我们可以创建两个指针,一个指针指向最后一个元素,一个指针指向首元素,两个指针向中间移动,这时候,由于只能先获得较大的数,我们用一个指针指向新创建的数组的最后一个元素,从后向前更新新数组.
class Solution {
public int[] sortedSquares(int[] nums) {
int size = nums.length - 1;
int i,j;
int k = size;
int[] result = new int [size + 1];
for(i = 0,j = size;i<=j;)
{
if(nums[i]*nums[i] < nums[j]*nums[j])
{
result[k] = nums[j] * nums[j];
k--;
j--;
}
else
{
result[k] = nums[i] * nums[i];
k--;
i++;
}
}
return result;
}
}这里我们 就用O(n)的时间复杂度解决了问题,仅仅遍历了一次数组,效率还是提升了不少的.
总结:
当出现有序数组的时候,我们可以考虑双指针的解法
Leetcode T209 长度最小的子数组
题目链接:209. 长度最小的子数组 - 力扣(LeetCode)
思路1: 暴力求解(现在跑不过)
这个时候我们很容易想到用两层for循环遍历两次数组,显然代码的时间复杂度是O(n^2),我们只需要给定一个sum记录子区间的总和,subLength记录总区间的长度,两个变量i和j记录子序列的起始位置和终止位置,在开始的时候定义一个result作为返回值.
class Solution {
public int minSubArrayLen(int target, int[] nums) {
int result = Integer.MAX_VALUE;
int i = 0;//开始位置
int j = 0;//结束为止
int sum = 0;
for(i = 0;i= target)
{
//取子序列的长度
subLength = j-i+1;
//找到长度最小的序列
result = result < subLength ? result : subLength;
break;
}
}
}
//如果result没变就是没有适合的元素的序列
return result == Integer.MAX_VALUE? 0: result;
}
} 总结
算法的总思路是第一次寻找起始位置,第二个for循环是寻找结束位置,从i开始累加,一旦累加的结果大于target就跳出,就说明从此时的i开始寻找到了满足条件的子序列,然后继续遍历以此类推.
思路2:滑动窗口
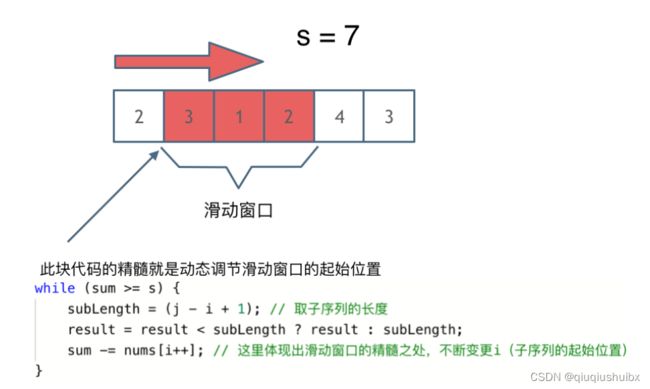
总体思想就是不断调整起始位置和终止位置,从而达到我们想要的效果
暴力解法是通过一个for循环是滑动窗口的起始位置,一个for循环是滑动窗口的结束位置,从而达到搜索整个数组的效果.
那么我们这个滑动窗口如何使用一个for循环来解决问题呢?
如果我们使用一个for循环代替起始位置,那难免会又想到暴力解法的思路上去,
所以这个for循环一定代表的是滑动窗口的末尾位置
举例说明:假设target的值是7,我们在 2 3 1 2 4 3这个数组里求最小的子数组
首先我们找到大于等于7的连续子数组 2 3 1 2, 条件:累计和>=7
这个时候我们的窗口就应该缩小了
而3 1 2是不满足的,所以我们继续向后找
3 1 2 4满足条件,缩小
1 2 4满足条件,缩小
2 4不满足条件 ,向前走
2 4 3满足条件,缩小
3 4 ,找到答案,返回2
注:图片取自于代码随想录网站,可以在文首点击查看详细解答.
解答代码:
class Solution {
public int minSubArrayLen(int target, int[] nums) {
//滑动窗口
int result = Integer.MAX_VALUE;
int i = 0;//左指针
int sum = 0;
for(int j = 0;j= target)
{
result = Math.min(result,j-i + 1);
sum -= nums[i++];
}
}
return result == Integer.MAX_VALUE?0:result;
}
} 注:不一定循环中套用循环就是O(n^2)的时间复杂度,这里是O(n*2)的时间复杂度也就是O(n)的时间复杂度,具体是么时候是O(n*n)什么时候是O(n+n).
这里我们可以看到暴力求解的时候两层都对i操作,也就是元素被操作了n*n次,就是O(n^2)的时间复杂度,这里是 在进窗口操作一次出窗口操作n次,所以是O(n)的时间复杂度.
总结:第一次做滑动窗口的问题,我认为更重要的是掌握这种让窗口动起来的同时不断更新子序列大小和位置的思想.
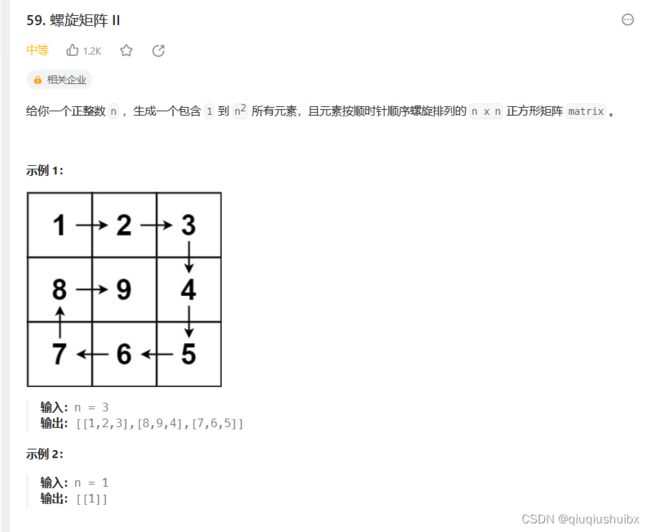
Leetcode T59 螺旋矩阵II
提示:1 <= n <= 20
思路:
题目的关键是保证循环变量中的不变量,我们的目的是用一个二维数组模拟实现这个矩阵,
定义一个起始坐标(start,start),我们定义一个while循环,循环次数是n/2次,那么有同学就会问了,我万一n是奇数怎么办,奇数的话我们的n就可以另外处理,定义一个loop,来控制每次执行完一圈我们向里进一圈.
重点:循环不变量的确定,这里我们一定要搞清楚每一次写入的区间,是左开右闭还是闭区间,这样才能保证代码的书写稳中不乱,这里我们选择的区间的左闭右开区间.
int start = 0; int count = 1; int loop = n/2; int i,j;
解答代码:
class Solution {
public int[][] generateMatrix(int n) {
int[][] arr = new int[n][n];
//起始地址
int start = 0;
//计数器
int count = 1;
//用来控制循环
int loop = 0;
//用来解决n等于奇数的问题
int mid = n/2;
int i,j;
while(loop++=loop;j--)
{
arr[i][j] = count++;
}
for(;i>=loop;i--)
{
arr[i][j] = count++;
}
start++;
}
if(n%2 == 1)
{
arr[mid][mid] = count;
}
return arr;
}
} 总结:
在遇到有序数组时,可以考虑二分法
一定要牢记循环不变量原则,找准循环中的不变量
找一个连续的子数组的总和值,可以想到滑动窗口解决问题