深度优先找出图中顶点U到顶点V的所有简单路径【C/C++】
目录
- 前言
- 步骤如下
-
- 1 对于邻接矩阵
-
- 1.1 创建邻接矩阵
- 1.2 初始化path数组和找到顶点U和顶点V的下标
- 1.3 FindPath()函数
- 1.4 测试结果
- 1.5 改进代码 感谢 @果冻的光滑 的指导和帮助!
- 2 对于邻接表
-
- 2.1 建立邻接表
- 2.2 初始化path数组和找到顶点U和顶点V的下标
- 2.3 FindPath()函数
- 2.4 测试结果
- 总结
前言
一直在复习数据结构,针对邻接矩阵书上有个算法是输出两个顶点之间的一条简单路径,这个听着很简单,仔细想了想,这不就和二叉树里输出根节点到r所指节点路径一样吗,维持一个栈,找到r指针就把栈弹空。
类似的,对于U和V顶点也是一样的,维持一个栈,在图中找到V顶点,直接弹空栈。这个对于一条简单路径来说很容易。
但是课后题有一个是输出U到V的全部简单路径,一涉及到回溯我这种榆木脑袋就头疼,思前想后,也是维持一个栈?但是弹空后怎么回溯到上一个递归的节点呢?
不断的思考,在耿国华的老师的数据结构里给我了一点启发,他利用一个pre数组来记录路线,当从某个顶点vi找到其邻接顶点vj进行访问时,将pre[j]置为i,这样在退出搜索后,就能根据pre数组从顶点v追溯到顶点u,从而输出这条从u到v的简单路径。
不得不说,耿国华老师不亏是国家教学名师,确实很厉害,但是我这个榆木脑袋是实在想不出来这么巧妙的方法。
我借鉴了耿国华老师的算法,按照自己的理解写了一个我能看懂的深度优先找出顶点U到顶点V的所有简单路径。
我这里用path数组代替耿老师的pre数组,思路是一样的,耿老师的比较精练,我自己写的虽然繁琐,但胜在自己看的懂,能复现。
步骤如下
1 对于邻接矩阵
1.1 创建邻接矩阵
//求顶点位置函数
int LocateVertex(AdjMatrix* G, VertexData v) {
int j, k;
for (k = 0; k < G->vexnum; k++) {
if (G->vertex[k] == v) {
j = k;
break;
}
}
return j;
}
//建立有向网图的邻接矩阵表示
void CreateAdjMatrix(AdjMatrix* G) {
int i, j, k, weight;
VertexData v1, v2;
printf("输入顶点数和边数\n");
scanf("%d,%d", &G->vexnum, &G->arcnum);
//对边表初始化
for (i = 0; i < G->vexnum; i++) {
for (j = 0; j < G->vexnum; j++) {
G->arcs[i][j].adj = ZHENGWUQIONG;//正无穷#define ZHENGWUQIONG 65535
}
}
//顶点表
for (i = 0; i < G->vexnum; i++) {
G->vertex[i]='A' + i;
}
printf("输入边表\n");
for (k = 0; k < G->arcnum; k++) {
scanf(" %c, %c,%d", &v1, &v2, &weight);
i = LocateVertex(G, v1);
j = LocateVertex(G, v2);
G->arcs[i][j].adj = weight;
//加上下面这行这就创建无向图。
G->arcs[j][i].adj = G->arcs[i][j].adj;
}
}
1.2 初始化path数组和找到顶点U和顶点V的下标
代码如下:
LocateVertex函数
int LocateVertex(AdjMatrix* G, VertexData v) {
int j, k;
for (k = 0; k < G->vexnum; k++) {
if (G->vertex[k] == v) {
j = k;
break;
}
}
return j;
}
初始化path数组和输入vi,vj
int* path = (int*)malloc(sizeof(int) * G.vexnum);
printf("输入要查询的两个节点,英文逗号隔开\n");
char ci, cj;
scanf(" %c, %c", &ci, &cj);
int vi = LocateVertex(&G, ci);
int vj = LocateVertex(&G, cj);
for (int i = 0; i < MAX; i++) {
visited[i] = 0;
}
FindPath(G, vi, vj, path, -1);
free(path);
1.3 FindPath()函数
接下来就是进入FindPath函数中。
path数组用来存储路径,相当于栈,d为路径长度,初始为-1,相当于栈顶指针。
将vi设为已访问,d++后,将其放入path数组中,如果vi和vj一样说明找到了v,那么就将path数组输出,每次输出都把d–,表示已经退出,并且将visited数组设为未访问,方便下一个节点的访问,但是因为递归的原因,如果返回上一个节点,那么path数组也会变为上一个节点的模样,这样就完成了回溯,简直完美。
但是visited数组是全局变量,因此在每次进入节点前都要将当时的path数组里的元素设为都已经访问过,这样就避免节点从vi=0开始搜索又搜回去了的情况。
代码如下:
void FindPath(AdjMatrix g, int vi, int vj, int* path, int d) {//d为栈顶元素下标初始为-1;
int i;
++d;
//把vi放到path数组中
path[d] = vi;
//设置vi为已访问
visited[vi] = 1;
//如果找到vj
if (vi == vj) {
int len = d;
//弹空path数组
for (int j = 0; j <= len; j++) {
printf("%c ", g.vertex[path[j]]);
//退栈
d--;
//不要把根节点设为未访问,这样容易成死循环。
if (j != 0) {
visited[path[j]] = 0;
}
}
printf("\n");
return;
}
for (i = 0; i < g.vexnum; i++) {
//在进入节点前,要把path数组里的元素都设置已访问,避免因为上一次输出path数组清零visited数组而导致的循环访问。
for (int len = d; len >= 0; len--) {
visited[path[len]] = 1;
}
if (!visited[i] && g.arcs[vi][i].adj != ZHENGWUQIONG) {
FindPath(g, i, vj, path, d);
}
}
//如果循环完了还没找到就退栈并且设置没访问过。等于走了个死胡同然后退出。
if (i == g.vexnum) {
visited[vi] = 0;
d--;
}
}
1.4 测试结果
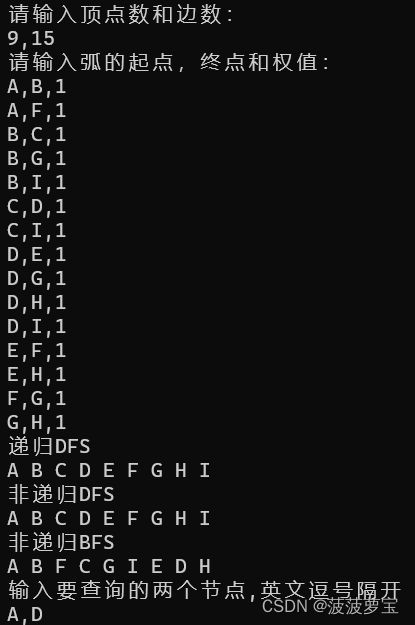
测试结果如下,找了个相当复杂的图。
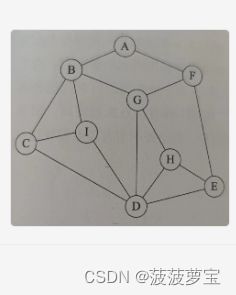


找一个最复杂的A,D

芜湖,简直完美!
1.5 改进代码 感谢 @果冻的光滑 的指导和帮助!
- 感谢 @果冻的光滑对于代码的改进!
不难发现,本文FindPath代码中17到19行 和26到28行做的工作是完全互补的,但对于代码的简明性有着较大的影响,做出一点小小的改进则可以使代码更加简洁明了
- 再次感谢 @果冻的光滑提供的两种方案!
方案一
如果找到目的节点,只许将递归进入的节点标记位设为未访问,则递归返回后再搜寻即可实现相同的前节点的路径搜寻。若搜寻相邻节点都没有路径,本层vi的访问位置为未访问退出即可。
void FindPath(AdjMatrix g, int vi, int vj, int* path, int d) {//d为栈顶元素下标初始为-1;
int i;
++d;
//把vi放到path数组中
path[d] = vi;
//设置vi为已访问
visited[vi] = 1;
//如果找到vj
if (vi == vj) {
int len = d;
//弹空path数组
for (int j = 0; j <= len; j++) {
printf("%c ", g.vertex[path[j]]);
}
visited[vi] = 0;
printf("\n");
return;
}
for (i = 0; i < g.vexnum; i++) {
if (!visited[i] && g.arcs[vi][i].adj != ZHENGWUQIONG) {
FindPath(g, i, vj, path, d);
}
}
//如果循环完了还没找到就退栈并且设置没访问过。等于走了个死胡同然后退出。
visited[vi] = 0;
}
方案二
弹出path数组后,无需return返回上一层,path数组在输出后将已访问的节点访问位置为0,在进入下一节点前再将path数组中的值置为已访问,以实现相同的前节点的路径搜寻。
void FindPath(AdjMatrix g, int vi, int vj, int* path, int d) {//d为栈顶元素下标初始为-1;
int i;
++d;
//把vi放到path数组中
path[d] = vi;
//设置vi为已访问
visited[vi] = 1;
//如果找到vj
if (vi == vj) {
int len = d;
//弹空path数组
for (int j = 0; j <= len; j++) {
printf("%c ", g.vertex[path[j]]);
if (j != 0) {
visited[path[j]] = 0;
}
}
printf("\n");
}
for (i = 0; i < g.vexnum; i++) {
for (int len = d; len >= 0; len--) {
visited[path[len]] = 1;
}
if (!visited[i] && g.arcs[vi][i].adj != ZHENGWUQIONG) {
FindPath(g, i, vj, path, d);
}
}
//如果循环完了还没找到就退栈并且设置没访问过。等于走了个死胡同然后退出。
if (i == g.vexnum) {
visited[vi] = 0;
}
}
综合对比两种方案,个人感觉方案一更加简洁,方案二延续我的执着于动态展现该层的访问情况的visited的来回标记显得过于繁琐。
再次感谢 @果冻的光滑提供的两种方案!
对于邻接表的FindPath数组也是类似的思路。
2 对于邻接表
2.1 建立邻接表
这里用的尾插法建立的边表。
//求顶点位置函数
int LocateVertex(AdjList* G, VertexData v) {
int j, k;
for (k = 0; k < G->vexnum; k++) {
if (G->vertexlist[k].data == v) {
j = k;
break;
}
}
return j;
}
//创建邻接表
void CreateAdjList(AdjList* adjlist) {
int i, j, k, weight;
char vi, vj;
printf("请输入顶点数和边数:\n");
scanf("%d,%d", &adjlist->vexnum, &adjlist->arcnum);
for (i = 0; i < adjlist->vexnum; i++) {
adjlist->vertexlist[i].data = 'A' + i;
adjlist->vertexlist[i].firstarc = NULL;
}
printf("请输入弧的起点,终点和权值:\n");
for (k = 0; k < adjlist->arcnum; k++) {
scanf(" %c ,%c,%d", &vi, &vj, &weight);
ArcNode* p = (ArcNode*)malloc(sizeof(ArcNode));
p->adjvex = LocateVertex(adjlist, vj);
ArcNode* tmp = adjlist->vertexlist[LocateVertex(adjlist, vi)].firstarc;
if (tmp == NULL) {
p->nextarc = adjlist->vertexlist[LocateVertex(adjlist, vi)].firstarc;
adjlist->vertexlist[LocateVertex(adjlist, vi)].firstarc = p;
}
else {
while (tmp->nextarc != NULL) {
tmp = tmp->nextarc;
}
p->nextarc = tmp->nextarc;
tmp->nextarc = p;
}
//无向图有
ArcNode* s = (ArcNode*)malloc(sizeof(ArcNode));
s->adjvex = LocateVertex(adjlist, vi);
ArcNode* tmp2 = adjlist->vertexlist[LocateVertex(adjlist, vj)].firstarc;
if (tmp2 == NULL) {
s->nextarc = adjlist->vertexlist[LocateVertex(adjlist, vj)].firstarc;
adjlist->vertexlist[LocateVertex(adjlist, vj)].firstarc = s;
}
else {
while (tmp2->nextarc != NULL) {
tmp2 = tmp2->nextarc;
}
s->nextarc = tmp2->nextarc;
tmp2->nextarc = s;
}
}
}
2.2 初始化path数组和找到顶点U和顶点V的下标
几乎和1.2一模一样
int* path = (int*)malloc(sizeof(int) * G.vexnum);
printf("输入要查询的两个节点,英文逗号隔开\n");
char ci, cj;
scanf(" %c, %c", &ci, &cj);
int vi = LocateVertex(&G, ci);
int vj = LocateVertex(&G, cj);
for (int i = 0; i < MAX; i++) {
visited[i] = 0;
}
FindPath(G, vi, vj, path, -1);
free(path);
2.3 FindPath()函数
和邻接矩阵的方法也是大同小异
//深度优先找出顶点u和顶点v的简单路径
void FindPath(AdjList g, int vi, int vj, int* path, int d) {
visited[vi] = 1;
d++;
path[d] = vi;
if (vi == vj) {
int i;
for (i = 0; i <= d; i++) {
printf("%c ", g.vertexlist[path[i]].data);
if (i != 0) {
visited[path[i]] = 0;
}
}
printf("\n");
return;
}
ArcNode* p = g.vertexlist[vi].firstarc;
while (p != NULL) {
for (int len = d; len >= 0; len--) {
visited[path[len]] = 1;
}
if (!visited[p->adjvex]) {
FindPath(g, p->adjvex, vj, path, d);
}
p = p->nextarc;
}
if (p == NULL) {
visited[vi] = 0;
d--;
}
}
2.4 测试结果
总结
这个算法虽然有点笨,但是我的榆木脑袋能理解,个人感觉很成功!