在无向图中求距离顶点v0的最短路径长度为K的所有顶点【C/C++】

---

前言

自己在看耿国华老师第二版数据结构中罪例题7.6在无向图中求距离顶点v0的最短路径长度为K的所有顶点按照耿国华老师的思路复现时怎么也复现不了，感觉有些问题，可能是我比较菜吧，我换了一种思路来实现。

---

一、耿老师的思路

从顶点v0开始进行广度优先搜索，将一步可达、两步可达…直至K步可达的所有顶点记录下来，同时用一个对联记录每个节点的层号，输出第K+1层的所有的顶点即为所求。

二、我的思路

1.分析思路

这里我认为耿老师用两个队列，一个存储节点，一个存储层数，想法很好，我这里延续，如果学过STL的话这里也可以采用一个unordered_map， unordered_map，key值保存层号，val保存顶点号，然后根据key值于设置的长度K进行比较，输出与K相同的哈希顺序链。对于map容器这里我只说个思路，实现也是很好实现的。
这里仍然按照耿老师的思路进行延续。
这里就不得不提非递归广度遍历无向图了，在这里面是将每一层的顶点依次输入进队列中，那么K步可达不就是输出以v0为顶点的第k层节点吗。实质上就是如果第一次出队的层号等于K，那么这时队列中所有的元素不就都是第k层的吗。
这样问题就简单了很多。
首先要写出非递归遍历无向图广度优先的算法。
这里采用邻接表来表示无向图。

2.非递归遍历无向图广度优先的算法

代码如下（示例）：

void NoReBroadFirstSearch(AdjList g, int v) {
	printf("%c ", g.vertexlist[v].data);
	visited[v] = 1;
	queue<int>Q;
	Q.push(v);
	while (!Q.empty()) {
		int front = Q.front();
		ArcNode* p = g.vertexlist[front].firstarc;
		while (p != NULL) {
			if (!visited[p->adjvex]) {
				printf("%c ", g.vertexlist[p->adjvex].data);
				visited[p->adjvex] = 1;
				Q.push(p->adjvex);
			}
			p = p->nextarc;
		}
		if (p == NULL) {
			Q.pop();
		}
	}
}
void NoReTraverseGrap(AdjList g) {
	for (int vi = 0; vi < g.vexnum; vi++) {
		visited[vi] = 0;
	}
	for (int vi = 0; vi < g.vexnum; vi++) {
		if (!visited[vi]) {
			NoReBroadFirstSearch(g, vi);
		}
	}
}

3.对于上一步算法的改进

延续耿老师的思路，采用双队列，一个存储节点，一个存储层号。
并将v0设置为已访问，初始层号为0。并将其放入队列中。

queue<int>QNode;
queue<int>QLevel;
visited[v0] = 1;
int level = 0;
QNode.push(v0);
QLevel.push(level);

只要队列不为空并且层数小于设置步数在出队前判断第一个出队的层号是否为步数K。
如果为步数K，那么该队列内所有元素均为步数K层的元素，弹空队列并输出。
如果不为步数K，则先将两个队列依次出队一个，在按照出队的顶点进行广度搜索，若未访问则入队。

4.具体代码

这里步数K为len，初始顶点为v0。

void FindNodeSetLenPath(AdjList g, int v0, int len) {
	queue<int>QNode;//顶点队列
	queue<int>QLevel;//层号队列
	for (int i = 0; i < g.vexnum; i++) {
		visited[i] = 0;//初始化访问标志数组
	}
	visited[v0] = 1;
	int level = 0;//初始层号
	QNode.push(v0);
	QLevel.push(level);
	while (!QNode.empty() && level <= len) {
		int curnode = QNode.front();
		level = QLevel.front();
		if (level == len) {
			while (!QNode.empty()) {
				int front = QNode.front();
				printf("%c ", g.vertexlist[front].data);
				QNode.pop();
			}
			return;
		}
		QNode.pop();
		QLevel.pop();
		ArcNode* p = g.vertexlist[curnode].firstarc;
		for (p; p != NULL; p = p->nextarc) {
			if (!visited[p->adjvex]) {
				visited[p->adjvex] = 1;
				QNode.push(p->adjvex);
				QLevel.push(level + 1);
			}
		}
	}
}

5.测试结果

这里依旧采用一个比较复杂的图。

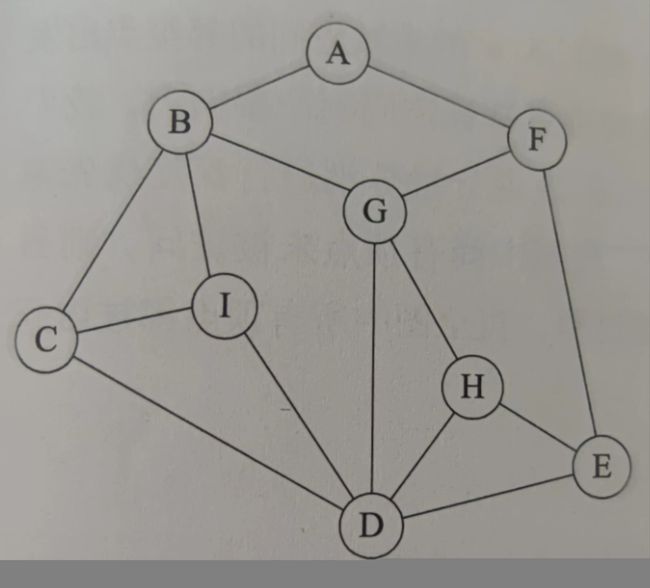
先求一下以G顶点步数为2的节点吧
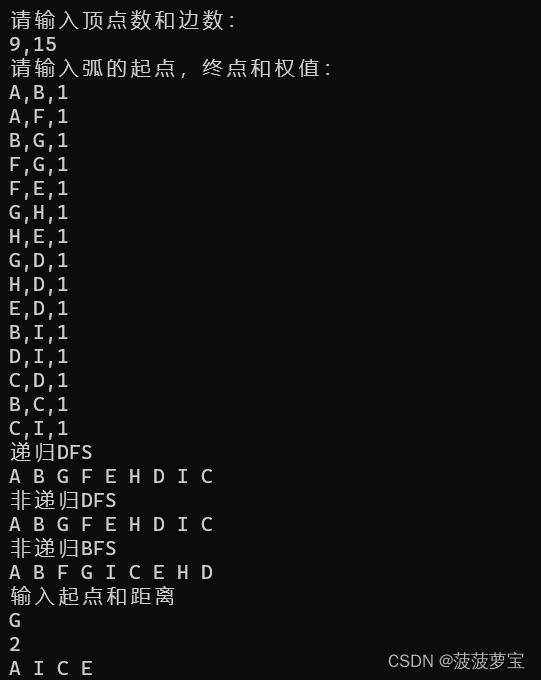以G顶点步数为2的节点为A I C E
这里可能有人要问了，你这广度遍历不对啊，你说的很有道理，是错的但是我不想改，hhh。这个受两个因素影响广度优先的顺序，一，你建立邻接表时采用的是头插法还是尾插法，第二个是你建立邻接表是节点的输入顺序。
但如果你是邻接矩阵的话就没这么多问题了，好烦！
我再把节点按逆时针好好输入一遍。

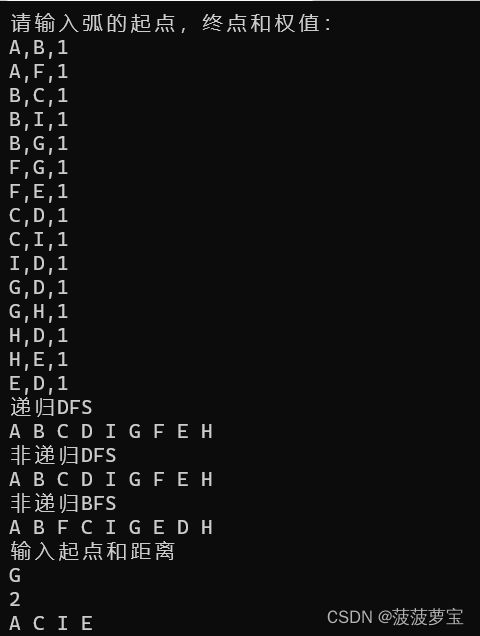
这里的广度遍历则就是按照逆时针顺序输出的节点，很完美。
再测验一个以H为顶点步数为3的节点

只有A节点符合
再测验以I节点步数为2的节点

有A G H E
测验正确！

---

总结

这里步数len可以理解成以v0顶点的第len层，这样问题就迎刃而解了。