算法设计与分析大作业之隐式图的搜索问题即八数码问题

说在前面：
对于这几个算法的研究中有一个问题没解决，就是如何更快速地检查某个状态是否已经走过，我这直接采用了遍历整棵树的方式，这样的效率太低了，其实可以采用哈希表或者其他方式将这个过程的时间复杂度降到O(1),感兴趣的自己试试吧，博主当时懒就没做。

隐式图的搜索问题
摘要：在人工智能领域中, 八数码问题一直都是一个游戏难题。本文介绍了八数码问题, 然后研究了两类算法在八数码问题中的求解过程。一类是无信息搜索算法，主要包括宽度优先搜索BFS和深度优先搜索DFS。另一类是有信息搜索算法，这里用的是启发式搜索算法即A*算法。本文对上述三种主要算法进行了实现与比对，代码运行环境为vs2019。

关键词：八数码问题 启发式搜索 宽度优先搜索 深度优先搜索

引言：八数码问题也称为九宫问题。在3X3的棋盘，摆有八个棋子，每个棋子上标有1至8的某一数字，不同棋子上标的数字不相同。棋盘上还有一个空格(以数字0来表示)，与空格相邻的棋子可以移到空格中。
要求解决的问题是:给出一个初始状态和一个目标状态，找出一种从初始转变成目标状态的移动棋子步数最少的移动步骤。
所谓问题的一个状态就是棋子在棋盘上的一种摆法。解八数码问题实际上就是找出从初始状态到达目标状态所经过的一-系列中间过渡状态。

一、问题描述
3х3九宫棋盘，放置数码为1~8的8个棋子，棋盘中留有一个空格，空格周围的棋子可以移动到空格中，从而改变棋盘的布局。
根据给定初始布局和目标布局，如何移动棋子才能从初始布局到达目标布局，找到一种最少步骤的移动方法。

二、问题分析
对于8数码问题我们首先应该想到的是问题是否可解，如何判断呢？这里给出如下判定结论：
将状态表示成一维的形式，求出除0（空格）之外所有数字的逆序数之和，也就是每个数字前面比它大的数字的个数的和，称为这个状态的逆序数。若两个状态的逆序奇偶性相同，则可相互到达，否则不可相互到达[1]。
例如：

S0表示成: 2 X 3 1 8 4 7 6 5
则:f(2)=0, f(3)=0, f(1)=2, f(8)=0, f(4)=1, f(7)=1, f(6)=2, f(5)=3
Sg表示成: 1 2 3 8 X 4 7 6 5
则:f(2)=0, f(3)=0, f(1)=2, f(8)=0, f(4)=1, f(7)=1, f(6)=2, f(5)=3
当f(a8)+f(a7)+……+f(a1)均为奇数或偶数时才能重排成功，所以，S0到Sg状态有解。
判断是否可解的问题解决了，用什么样的搜索算法找到移动路径呢？

其实，不管哪种搜索，都可以统一用这样的形式表示: 搜索的对象是一个图，它面向一个问题，不一定有明确的存储形式，但它里面的每一个结点都有可能是一个解(可行解)，搜索的目的有两个方面，或者求可行解，或者从可行解集中求最优解。

搜索算法可分为两大类:无信息的搜索算法和有信息的搜索算法。无信息的搜索又称盲目搜索，其特点是只要问题状态可以形式化表示，原则上就可用使用无信息的搜索，无信息搜索有如下常见的几种搜索策略:广度优先搜索、代价一致搜索、深度优先搜索、深度有限搜索、迭代深入优先搜索、双向搜索。我们说DFS和BFS都是蛮力搜索，因为它们在搜索到一个结点时，在展开它的后续结点时，是对它们没有任何‘认识’ 的，它认为它的孩子们都是一样的‘优秀’，但事实并非如此，后续结点是有好有坏的。好，就是说它离目标结点‘近’，如果优先处理它，就会更快的找到目标结点，从而整体上提高搜索性能。

为了改善上面的算法，我们需要对展开后续结点时对子结点有所了解，这里需要一个估值函数，估值函数就是评价函数，它用来评价子结点的好坏，因为准.确评价是不可能的，所以称为估值。这就是我们所谓的有信息搜索。如果估值函数只考虑结点的某种性能上的价值，而不考虑深度，比较有名的就是有序搜索(Ordered-Search)，它着重看好能否找出解，而不看解离起始结点的距离(深度)。如果估值函数考虑了深度，或者是带权距离(从起始结点到目标结点的距离加权和)，那就是A*。简单的来说A*就是将估值函数分成两个部分，一个部分是路径价值，另一个部分是一般性启发价值，合在一起算估整个结点的价值。

三、宽度优先搜索
1.算法设计
树的节点结构如下，节点类具有一个父类指针和四个孩子指针，一个保存九宫格信息的二维数组。

四个孩子指针对应了空格下一次移动的四种可能方向，即向上，向下，向左，向右。所以以这样的节点构造出的树是一颗四叉树。
八数码类的设计如下：
树的根节点存储了初始状态，寻找最短路径的过程就是通过宽度优先不断扩展四叉树的叶节点的过程。

BFS算法流程：
(1)调用isexist()函数判断是否有可行解。
(2)如果有可行解，将根节点start放入队列dict中。
(3)从队列dict中取出一个节点指针，判断该节点存储的状态与目的状态target是否相同。
如果相同，调用print()函数从该节点往树的根节点进行遍历，将路径存储在栈shortpath中，最后逆序输出。
如果不同，调用grow()函数判断该节点对应的形态下一步有几个可行移动方向，这里需要调用compare()函数对可行方向筛选，剔除已经遍历过的情形，将最终的可行方向构造成心得节点作为树的扩展叶节点，并将这些节点的指针存入队列dict。
(4)回到(3)。

2.算法分析
下面是宽度优先搜索算法的工作过程，可以看到宽度优先搜索就是一层层地在扩展叶节点，直到找到目的状态。

因为构造了一颗四叉树，宽度优先搜索算法最坏时间复杂度O(4^{n),空间复杂度也为O(4}n)。

3.运行结果

四、深度优先搜索
1.算法设计
树的节点结构与宽度优先搜索相同：

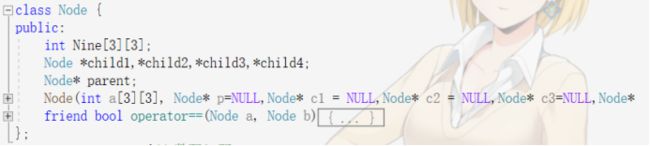
八数码类的设计中只是将dict从队列类型变量改为了栈类型，除此再无任何变动，所以从代码上来看宽度优先搜索与深度优先搜索的实现是非常类似的，特别是当使用非递归方式实现两个算法的时候。

DFS算法流程与BFS完全相同：
(1)调用isexist()函数判断是否有可行解。
(2)如果有可行解，将根节点start放入栈dict中
(3)从栈dict中取出一个节点指针，判断该节点存储的状态与目的状态target是否相同。
如果相同，调用print()函数从该节点往树的根节点进行遍历，将路径存储在栈shortpath中，最后逆序输出。
如果不同，调用grow()函数判断该节点对应的形态下一步有几个可行移动方向，这里需要调用compare()函数对可行方向筛选，剔除已经遍历过的情形，将最终的可行方向构造成心得节点作为树的扩展叶节点，并将这些节点的指针存入栈dict。
(4)回到(3)。

2.算法分析
下面是深度优先搜索算法的工作过程，可以看到深度优先搜索是一根根树枝地扩展叶节点，当一根树枝扩展到最深时又回到上一个分叉处扩展另一根树枝。

因为构造了一颗四叉树，深度优先搜索算法最坏时间复杂度O(4^{n),空间复杂度也为O(4}n)，与宽度优先搜索相同。

3.运行结果

五、启发式搜索(A*算法)
1.算法设计
启发式策略：
启发式搜索就是在状态空间种的搜索，对每一个搜索的位置进行评估，得到最好的位置，再从这个位置进行搜索直到目标。这样可以省略大量无谓的搜索路径，提高了效率。
启发中的估价是用估价函数表示的：
如：f(n)=g(n)+h(n)
f(n) ：结点n 的估价函数；
g(n) ：在状态空间中从初始节点S0到n节点的实际代价。（从初始状态变换到当前状态所移动的步数/或即为该节点的深度。）
h(n) ：是从n到目标节点Sg最佳路径的估计代价。（可采用当前状态各个数字棋子不在目标状态位置的个数，即错位数。）
例如对于下面的情况：g(n)=0，h(n)=5，f(n)=g(n)+h(n)=5。
g(n)： 从初始节点到当前节点的步数（层数）
h(n)： 当前节点“不在位”的棋格数

节点结构设计：

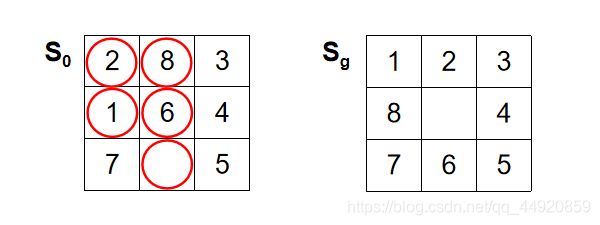
节点结构比之前多了价值和层数两个变量，以及>重载函数。

八数码类设计：

类的设计没有太大改动，主要是dict变量类型再次发生变化，这一次是双端队列类型。另外grow()函数里增添了对节点设置f值的语句。

算法流程：
(1)调用isexist()函数判断是否有可行解。
(2)如果有可行解，将根节点start放入队列dict中。
(3)对dict按节点价值进行从小到大排序。
(4)从队列dict队首中取出一个节点指针，判断该节点存储的状态与目的状态target是否相同。
如果相同，调用print()函数从该节点往树的根节点进行遍历，将路径存储在栈shortpath中，最后逆序输出。
如果不同，调用grow()函数判断该节点对应的形态下一步有几个可行移动方向，这里需要调用compare()函数对可行方向筛选，剔除已经遍历过的情形，将最终的可行方向构造成心得节点作为树的扩展叶节点，这个过程应包含对节点价值的计算，并将这些节点的指针存入队列dict。
(5)最后回到(3)。
2.算法分析
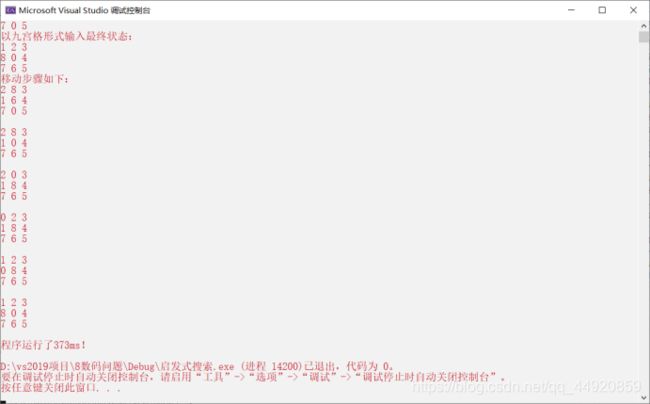
下面是启发式策略工作过程的直观展示，可以看出启发式搜索寻找目标状态的过程很迅速。

A算法的时间和空间复杂度不太好计算，但我们能确定的是，
A算法的时间和空间复杂度一定是远远小于O(4^n)的。当n很大的时候，A*算法的效率将比深度优先搜索和宽度优先搜索高许多。
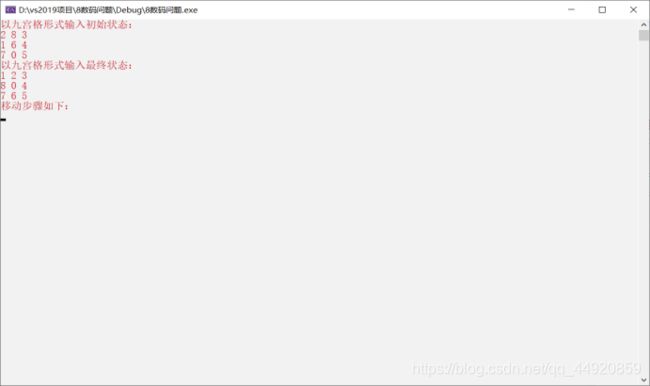
3.运行结果

六、对比与总结
1.对比
对于如下初始状态与目标状态，我们可以看一下三种算法求解出结果各自所需时长

启发式搜索：

宽度优先搜索，这是程序运行了一分钟的样子：

深度优先搜索，这也是程序运行了一分钟的样子：

从以上结果可以看出，深度优先搜索和广度优先搜索在效率上与A算法真的是天壤之别，A算法仅用了0.4秒不到给出了结果，而深度优先和广度优先算法运行一分钟都没能求解成功。

2.总结

本文对八数码问题的几种解决方案进行了实现与对比。尽管深搜、广搜和启发式搜索在代码实现上难度都差不多，但是启发式搜索的时间和空间效率都远远优于深度优先和广度优先算法。所以在这种隐式图的问题中，A*算法永远是一个不错的选择，而深度优先和广度优先算法可能更多适合于显示图的搜索问题。

我对这三种算法的实现还有一个很大的不足之处，就是在判断某个节点是否已经搜索过时我选择了遍历整棵树的节点与之进行比对，这可能是造成我所实现的BFS和DFS效率过于低下的原因。后来我想到应该使用哈希表来存储已经搜寻过的节点，这样的话“判断某个节点是否已经搜索过”的时间复杂度就能变成O(1)。

七、参考文献
[1]杨正洪.人工智能与大数据技术导论.北京.清华大学出版社
[2]邓俊辉.数据结构.北京.清华大学出版社
[3]吴陈.数据结构.科学出版社
八、附录``
广搜代码：

#pragma comment(lib, "winmm.lib ")
#include 
#include
#include
#include
using namespace std;
class Node {
public:
	int Nine[3][3];
	Node *child1,*child2,*child3,*child4;
	Node* parent;
	Node(int a[3][3], Node* p=NULL,Node* c1 = NULL,Node* c2 = NULL,Node* c3=NULL,Node* c4=NULL)
	{
		for (int i = 0; i < 3; i++)
			for (int j = 0; j < 3; j++)
				Nine[i][j] = a[i][j];
		parent = p;
		child1 = c1;
		child2 = c2;
		child3 = c3;
		child4 = c4;
	}
	friend bool operator==(Node a, Node b)//重载==，比较两个九宫格是否相同
	{
		bool flag = 1;
		for (int i = 0; i < 3; i++)
			for (int j = 0; j < 3; j++)
				if (a.Nine[i][j] != b.Nine[i][j])return false;
		return true;
	}
};
class EightPuzzle {//8数码问题
private:
	Node* start;//初始状态
	Node* target;//目标状态
	queue<Node*> dict;//BFS中存储未遍历过的节点
	stack<Node> shortpath;//存储最短路径
public:
	EightPuzzle(int a[3][3], int b[3][3]) { start = new Node(a); target = new Node(b); }
	bool compare(Node* root,Node p);//搜索当前准备添加的新路径是否已经出现过
	void grow(Node *leaf);//从叶节点扩展新的不重复的路径
	void swap(int& a, int& b);
	void BFS();
	void print();
	bool isexist();//检测是否有路径能到达目标状态
};
bool EightPuzzle::isexist() {
	int a = 0, b = 0;
	for (int i = 0; i < 9; i++)
		for (int j = 0; j < i; j++)
			if (start->Nine[j] > start->Nine[i])a++;
	for (int i = 0; i < 9; i++)
		for (int j = 0; j < i; j++)
			if (target->Nine[j] > target->Nine[i])b++;
	if (a % 2 == b % 2)return 1;
	else return 0;
}
bool EightPuzzle::compare(Node* root,Node p){
	if (root!=NULL &&*root== p)return 1;
	if (root->child1 != NULL)compare(root->child1, p);
	if (root->child2 != NULL)compare(root->child2, p);
	if (root->child3 != NULL)compare(root->child3, p);
	if (root->child4 != NULL)compare(root->child4, p);
	return 0;
}
void EightPuzzle::swap(int& a, int& b) {
	int tmp = a;
	a = b; 
	b = tmp;
}
void EightPuzzle::grow(Node* leaf) {
	int a[3][3];
	for(int i=0;i<3;i++)
		for(int j=0;j<3;j++)
			 a[i][j]= leaf->Nine[i][j];
	int x = 0, y = 0;
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 3; j++) {
			if (a[i][j] == 0) { x = i; y = j; }
		}
	}
	if ((x - 1) >= 0)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x - 1][y]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child1 = q; q->parent = leaf; dict.push(q);
		}
	}
	if (x + 1 <= 2)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x + 1][y]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child2 = q; q->parent = leaf; dict.push(q);
		}
	}
	if (y - 1 >= 0)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x][y-1]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child3 = q; q->parent = leaf; dict.push(q);
		}
	}
	if (y + 1 <= 2)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x][y+1]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child4 = q; q->parent = leaf; dict.push(q);
		}
	}
}
void EightPuzzle::BFS() {
	if (isexist() == 0) { cout << "没有移动方法能从起始状态目标状态！"; exit(1); }
	else { cout << "移动步骤如下：\n"; }
	Node *p = start;
	dict.push(p);
	while (!(*p == *target))
	{
		dict.pop();
		grow(p);
		p = dict.front();
	}
	target = p;
	Node *q = target;
	while (q != NULL)
	{
		shortpath.push(*q);
		q = q->parent;
	}
}
void EightPuzzle::print() {
	while (!shortpath.empty()) {
		Node p = shortpath.top();
		shortpath.pop();
		for (int i = 0; i < 3; i++) {
			for (int j = 0; j < 3; j++)
				cout << p.Nine[i][j]<<' ';
			cout << endl;
		}
		cout << endl;
	}
}
int main() {
	int a[3][3] ;
	int b[3][3] ;
	cout << "以九宫格形式输入初始状态：\n";
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			cin >> a[i][j];
	cout<< "以九宫格形式输入最终状态：\n";
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			cin >> b[i][j];
	EightPuzzle test(a, b);

	DWORD Start = timeGetTime();

	test.BFS();
	test.print();

	DWORD End = timeGetTime();

	cout << "程序运行了" << End - Start << "ms！\n";
	return 0;
}

深搜代码：

#pragma comment(lib, "winmm.lib ")
#include 
#include
#include
using namespace std;
class Node {
public:
	int Nine[3][3];
	Node* child1, * child2, * child3, * child4;
	Node* parent;
	Node(int a[3][3], Node* p = NULL, Node* c1 = NULL, Node* c2 = NULL, Node* c3 = NULL, Node* c4 = NULL)
	{
		for (int i = 0; i < 3; i++)
			for (int j = 0; j < 3; j++)
				Nine[i][j] = a[i][j];
		parent = p;
		child1 = c1;
		child2 = c2;
		child3 = c3;
		child4 = c4;
	}
	friend bool operator==(Node a, Node b)//重载==，比较两个九宫格是否相同
	{
		bool flag = 1;
		for (int i = 0; i < 3; i++)
			for (int j = 0; j < 3; j++)
				if (a.Nine[i][j] != b.Nine[i][j])return false;
		return true;
	}
};
class EightPuzzle {//8数码问题
private:
	Node* start;//初始状态
	Node* target;//目标状态
	stack<Node*> dict;//DFS中存储未遍历过的节点
	stack<Node> shortpath;//存储最短路径
public:
	EightPuzzle(int a[3][3], int b[3][3]) { start = new Node(a); target = new Node(b); }
	bool compare(Node* root, Node p);//搜索当前准备添加的新路径是否已经出现过
	void grow(Node* leaf);//从叶节点扩展新的不重复的路径
	void swap(int& a, int& b);
	void DFS();
	void print();
	bool isexist();//检测是否有路径能到达目标状态
};
bool EightPuzzle::isexist() {
	int a = 0, b = 0;
	for (int i = 0; i < 9; i++)
		for (int j = 0; j < i; j++)
			if (start->Nine[j] > start->Nine[i])a++;
	for (int i = 0; i < 9; i++)
		for (int j = 0; j < i; j++)
			if (target->Nine[j] > target->Nine[i])b++;
	if (a % 2 == b % 2)return 1;
	else return 0;
}
bool EightPuzzle::compare(Node* root, Node p) {
	if (root != NULL && *root == p)return 1;
	if (root->child1 != NULL)compare(root->child1, p);
	if (root->child2 != NULL)compare(root->child2, p);
	if (root->child3 != NULL)compare(root->child3, p);
	if (root->child4 != NULL)compare(root->child4, p);
	return 0;
}
void EightPuzzle::swap(int& a, int& b) {
	int tmp = a;
	a = b;
	b = tmp;
}
void EightPuzzle::grow(Node* leaf) {
	int a[3][3];
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			a[i][j] = leaf->Nine[i][j];
	int x = 0, y = 0;
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 3; j++) {
			if (a[i][j] == 0) { x = i; y = j; }
		}
	}
	if ((x - 1) >= 0)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x - 1][y]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child1 = q; q->parent = leaf; dict.push(q);
		}
	}
	if (x + 1 <= 2)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x + 1][y]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child2 = q; q->parent = leaf; dict.push(q);
		}
	}
	if (y - 1 >= 0)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x][y - 1]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child3 = q; q->parent = leaf; dict.push(q);
		}
	}
	if (y + 1 <= 2)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x][y + 1]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child4 = q; q->parent = leaf; dict.push(q);
		}
	}
}
void EightPuzzle::DFS() {
	if (isexist() == 0) { cout << "没有移动方法能从起始状态目标状态！"; exit(1); }
	else { cout << "移动步骤如下：\n"; }
	Node* p = start;
	dict.push(p);
	while (!(*p == *target))
	{
		dict.pop();
		grow(p);
		p = dict.top();
	}
	target = p;
	Node* q = target;
	while (q != NULL)
	{
		shortpath.push(*q);
		q = q->parent;
	}
}
void EightPuzzle::print() {
	while (!shortpath.empty()) {
		Node p = shortpath.top();
		shortpath.pop();
		for (int i = 0; i < 3; i++) {
			for (int j = 0; j < 3; j++)
				cout << p.Nine[i][j] << ' ';
			cout << endl;
		}
		cout << endl;
	}
}
int main() {
	int a[3][3];
	int b[3][3];
	cout << "以九宫格形式输入初始状态：\n";
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			cin >> a[i][j];
	cout << "以九宫格形式输入最终状态：\n";
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			cin >> b[i][j];
	EightPuzzle test(a, b);

	DWORD Start = timeGetTime();

	test.DFS();
	test.print();

	DWORD End = timeGetTime();

	cout << "程序运行了" << End - Start << "ms！\n";
	return 0;
}

A*算法代码：

#pragma comment(lib, "winmm.lib ")
#include 
#include
#include
#include
#include

using namespace std;
class Node {
public:
	int Nine[3][3];
	int f;//价值
	int h;//层数
	Node* child1, * child2, * child3, * child4;
	Node* parent;
	Node(int a[3][3], Node* p = NULL, Node* c1 = NULL, Node* c2 = NULL, Node* c3 = NULL, Node* c4 = NULL,int H=0)
	{
		for (int i = 0; i < 3; i++)
			for (int j = 0; j < 3; j++)
				Nine[i][j] = a[i][j];
		parent = p;
		child1 = c1;
		child2 = c2;
		child3 = c3;
		child4 = c4;
		h = H;
	}
	void setf(int g) { f = h + g; }//设置价值，g为当前节点“不在位”的棋格数
	friend bool operator==(Node a, Node b)//重载==，比较两个九宫格是否相同
	{
		bool flag = 1;
		for (int i = 0; i < 3; i++)
			for (int j = 0; j < 3; j++)
				if (a.Nine[i][j] != b.Nine[i][j])return false;
		return true;
	}
	friend bool operator>(Node a, Node b)//重载>，比较两个节点价值大小
	{
		if (a.f > b.f)return 1;
		else return 0;
	}
};
class EightPuzzle {//8数码问题
private:
	Node* start;//初始状态
	Node* target;//目标状态
	deque<Node*> dict;//Astar中存储未遍历过的节点
	stack<Node> shortpath;//存储最短路径
public:
	EightPuzzle(int a[3][3], int b[3][3]) { start = new Node(a); target = new Node(b); }
	bool compare(Node* root, Node p);//搜索当前准备添加的新路径是否已经出现过
	void grow(Node* leaf);//从叶节点扩展新的不重复的路径
	void swap(int& a, int& b);
	void Astar();
	void print();
	bool isexist();//检测是否有路径能到达目标状态
};
bool EightPuzzle::isexist() {
	int a = 0, b = 0;
	for (int i = 0; i < 9; i++)
		for (int j = 0; j < i; j++)
			if (start->Nine[j] > start->Nine[i])a++;
	for (int i = 0; i < 9; i++)
		for (int j = 0; j < i; j++)
			if (target->Nine[j] > target->Nine[i])b++;
	if (a % 2 == b % 2)return 1;
	else return 0;
}
bool EightPuzzle::compare(Node* root, Node p) {
	if (root != NULL && *root == p)return 1;
	if (root->child1 != NULL)compare(root->child1, p);
	if (root->child2 != NULL)compare(root->child2, p);
	if (root->child3 != NULL)compare(root->child3, p);
	if (root->child4 != NULL)compare(root->child4, p);
	return 0;
}
void EightPuzzle::swap(int& a, int& b) {
	int tmp = a;
	a = b;
	b = tmp;
}
void EightPuzzle::grow(Node* leaf) {
	int a[3][3];
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			a[i][j] = leaf->Nine[i][j];
	int x = 0, y = 0;
	for (int i = 0; i < 3; i++) {
		for (int j = 0; j < 3; j++) {
			if (a[i][j] == 0) { x = i; y = j; }
		}
	}
	if ((x - 1) >= 0)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x - 1][y]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child1 = q; q->parent = leaf; 
			q->h = leaf->h + 1;
			int count = 0;
			for (int i = 0; i < 3; i++)
				for (int j = 0; j < 3; j++)
					if (q->Nine[i][j] != target->Nine[i][j])count++;
			q->setf(count);
			dict.push_back(q);
		}
	}
	if (x + 1 <= 2)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x + 1][y]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child1 = q; q->parent = leaf;
			q->h = leaf->h + 1;
			int count = 0;
			for (int i = 0; i < 3; i++)
				for (int j = 0; j < 3; j++)
					if (q->Nine[i][j] != target->Nine[i][j])count++;
			q->setf(count);
			dict.push_back(q);
		}
	}
	if (y - 1 >= 0)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x][y - 1]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child1 = q; q->parent = leaf;
			q->h = leaf->h + 1;
			int count = 0;
			for (int i = 0; i < 3; i++)
				for (int j = 0; j < 3; j++)
					if (q->Nine[i][j] != target->Nine[i][j])count++;
			q->setf(count);
			dict.push_back(q);
		}
	}
	if (y + 1 <= 2)
	{
		Node p = *leaf;
		swap(p.Nine[x][y], p.Nine[x][y + 1]);
		if (!compare(start, p))
		{
			Node* q = new Node(p); leaf->child1 = q; q->parent = leaf;
			q->h = leaf->h + 1;
			int count = 0;
			for (int i = 0; i < 3; i++)
				for (int j = 0; j < 3; j++)
					if (q->Nine[i][j] != target->Nine[i][j])count++;
			q->setf(count);
			dict.push_back(q);
		}
	}
}
void EightPuzzle::Astar() {
	if (isexist() == 0) { cout << "没有移动方法能从起始状态到目标状态！"; exit(1); }
	else { cout << "移动步骤如下：\n"; }
	Node* p = start;
	dict.push_back(p);
	while (!(*p == *target))
	{
		dict.pop_front();
		grow(p);
		sort(dict.begin(), dict.end());
		p = dict.front();
	}
	Node* q = p;
	while (q != NULL)
	{
		shortpath.push(*q);
		q = q->parent;
	}
}
void EightPuzzle::print() {
	while (!shortpath.empty()) {
		Node p = shortpath.top();
		shortpath.pop();
		for (int i = 0; i < 3; i++) {
			for (int j = 0; j < 3; j++)
				cout << p.Nine[i][j] << ' ';
			cout << endl;
		}
		cout << endl;
	}
}
int main(int argc, char* argv[]) {
	int a[3][3];
	int b[3][3];
	cout << "以九宫格形式输入初始状态：\n";
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			cin >> a[i][j];
	cout << "以九宫格形式输入最终状态：\n";
	for (int i = 0; i < 3; i++)
		for (int j = 0; j < 3; j++)
			cin >> b[i][j];
	EightPuzzle test(a, b);

	DWORD Start = timeGetTime();

	test.Astar();
	test.print();

	DWORD End = timeGetTime();

	cout << "程序运行了" << End - Start << "ms！\n";
	return 0;
}