非静压模型SWASH学习（6）——二维波浪变形模拟算例（Wave transformation over an elliptic shoal on a sloped bottom）

SWASH是由Delft大学开发，用于模拟非静压条件下的水动力/波浪运动的数值模型。
与模型原理相关的内容详见以下论文：

1. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters (Marcel Zijlema, Guus Stelling, Pieter Smit)¹
2. Computation of free surface waves in coastal waters with SWASH on unstructured grids (Marcel Zijlema)²
3. An accurate and efficient finite-difference algorithm for non-hydrostatic free-surface flow with application to wave propagation³

其中，第2篇论文是描述了SWASH模型的最新功能，即可支持非结构化三角形网格。不过，本blog提及的算法、设置以swash结构化网格的版本为对象，不涉及非机构化网格。
注：有些指令、参数已经在前面的博客中进行讲解了，故之后不会再详细说明；相关内容详见之前的博文。也希望大家能留言，来相互交流！

SWASH主页：https://swash.sourceforge.io/
模型手册：https://swash.sourceforge.io/online_doc/swashuse/swashuse.html

算例简介

本算例模拟了波浪在不规则地形上的传播、折射和衍射现象。本例的模型配置详见Stelling&Zijlema³或Berkhoff et al. (1982)⁴。最后，我们将模拟结果与Berkhoff等人的论文中物理实验的结果数据进行比较。
模型输入文件及相关数据可下载于【传送门】。若要运行此算例，请将此下载的压缩文件解压，将含有.sws、 .wlv和 .bot后缀的所有文件解压至swash.exe所在的目录下。

模型配置

首先，定义一个与笛卡尔坐标系（x，y）夹角为-20°的坐标系统（x’，y’）。

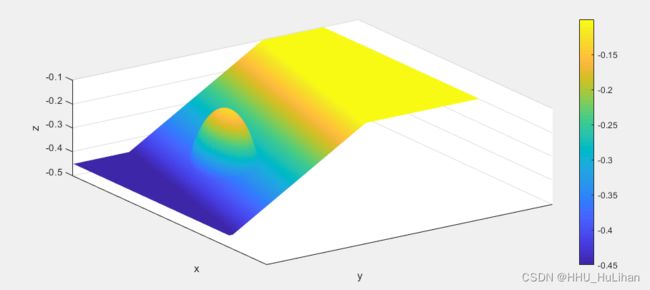
斜坡与x’的方向平行。在斜坡上有一个凸起的小丘，小丘的平面形态为：
$$(\frac{x^{\prime }}{4}{)}^2+(\frac{y^{\prime }}{3}{)}^2=1$$
小丘的高度d为：
$$d=-0.3+0.5\sqrt{1-{\frac{x^{\prime }}{5}}^2-{\frac{y^{\prime }}{3.75}}^2}$$
所以底高程可以表示为：
$$z_b=-min[0.45,max(0.10,0.45-0.02(5.84+y^{\prime }))]+d$$
波浪从y = -10m的位置向着y的正方向入射。入射波为规则波列，波高H₀=4.64cm，周期T₀=1.0s。
为最大限度地消除波浪反射和边界对计算域的影响，在模型的另一端y = 20m处设置了辐射边界和海绵层的组合。
此外，物理实验中观测了8个断面的水面变化，这8个断面的位置如上图所示。

补充：计算域三维图如下所示

网格及参数设置

网格与地形

本算例的参数文件中省略了MODE和vert，故采用默认设置 MODE TWODimensional和VERT 1，即该数值模型为平面的二维模型。

CGRID -10. -10. 0. 20. 35. 200 700
$
INPGRID BOTTOM -10. -10. 0. 200 700 0.1 0.05
READINP BOTTOM 1. 'l41berkh.bot' 3 0 FREE

计算域的原点为(-10.0m, -10.0m)，两个方向的长度分别为20.0m和35.0m。x方向和y方向的网格数分别为200和700，即Δx=0.1m、Δy=0.05m。
之后，通过INPGRID和READINP指令，从文件’l41berkh.bot’中读取地形数据。

初始条件与边界条件

INIT zero
$
BOU SIDE S CCW BTYPE WEAK CON REG 0.0464 1.
BOU SIDE N CCW BTYPE RADIATION
SPON UP 5.

INIT指令设定初始条件，即初始时水位和流速值均为零。
BOU指令设定了模型的下侧（South, y=0）和上侧（North, y=35.0m）边界的边界条件。对于波浪入射的下侧边界，模型采用了弱反射（WEAKREFL）设置，并设定规则入射波（REGular）的波高h=0.0464m，波周期per=1.0s。对于上侧边界，本模型采用了辐射边界（RADIATION）和海绵边界层（SPON）的组合。其中SPON之后的’UP‘同’North‘；参数width=5.0m，表示，边界层的厚度为5.0m（即海绵边界层位于y=15~20m）。这样的组合能够最大程度地消解传播到上侧边界的波浪，并壁面上侧边界对波浪的反射。

数值求解方法

NONHYDrostatic
$
DISCRET CORRDEP MINMOD

首先，模型采用了非静压模拟（NONHYDrostatic）的方法。对于流速计算点的水位和水深，模型采用MINMOD函数进行求解。

模型输出

QUANT DIST HEXP 10.
$
CURVE 'sect1' -4.75 1. 380  4.75  1.
CURVE 'sect2' -4.75 3. 380  4.75  3.
CURVE 'sect3' -4.75 5. 380  4.75  5.
CURVE 'sect4' -4.75 7. 380  4.75  7.
CURVE 'sect5' -4.75 9. 380  4.75  9.
CURVE 'sect6'  2.00 0. 220  2.00 11.
CURVE 'sect7'  0.00 0. 220  0.00 11.
CURVE 'sect8' -2.00 0. 220 -2.00 11.
$
TABLE 'sect1' NOHEAD 'section1.tbl' TSEC XP WATL VEL OUTPUT 000030.000 0.01 SEC
TABLE 'sect2' NOHEAD 'section2.tbl' TSEC XP WATL VEL OUTPUT 000030.000 0.01 SEC
TABLE 'sect3' NOHEAD 'section3.tbl' TSEC XP WATL VEL OUTPUT 000030.000 0.01 SEC
TABLE 'sect4' NOHEAD 'section4.tbl' TSEC XP WATL VEL OUTPUT 000030.000 0.01 SEC
TABLE 'sect5' NOHEAD 'section5.tbl' TSEC XP WATL VEL OUTPUT 000030.000 0.01 SEC
TABLE 'sect6' NOHEAD 'section6.tbl' TSEC YP WATL VEL OUTPUT 000030.000 0.01 SEC
TABLE 'sect7' NOHEAD 'section7.tbl' TSEC YP WATL VEL OUTPUT 000030.000 0.01 SEC
TABLE 'sect8' NOHEAD 'section8.tbl' TSEC YP WATL VEL OUTPUT 000030.000 0.01 SEC
$
BLOCK 'COMPGRID' NOHEAD 'l41ber01.mat' LAY 3 XP YP BOTL WATL VKSI VETA OUTPUT 000030.000 5 SEC

输出格式设置分为两部分，第一部分设置了各个监测面的位置。这部分的设置采用CURVE指令，它可在计算域中定义一条线，之后可输出该线上的物理量的值；其格式如下：

'sname’为各个监测面的名字，xp1和yp1表示所画线条的起始点，而xp和yp表示所画线条的结束点。在这条线上，我们将定义int等分点（即在两个端点内生成 int-1 个点）；之后，这些点上的值将被输出。以CURVE ‘sect1’ 为例，我们可知这条线的从
(-4.75m, 1.0m)开始，到(4.75m, 1.0m)结束，并在线段内部生成其(380-1)个等分点。

第二部分则利用TABLE指令，以无文件头表格的方式输出了各个监测点的x或y坐标（XP或YP）、水位（WATL）、三个方向的速度（VEL），以及对应的时间（TSEC）；输出数据即水位时间序列。输出的时间间隔为 0.01s，起始时间为 00：00：30.000。
此外，通过该TABLE的设置可以看出，每个tbl文件共含6列数据（第一列为时间，第二列为坐标值，第三列为水位值，第四到第六列为x、y和z方向的流速值）

计算时间

COMPUTE 000000.000 0.01 SEC 000035.000

模型计算时间为 35.0s，时间步长为 0.01s。

模拟结果

将参数文件 l41ber01.sws，以及地形数据文件 l41ber01.bot 复制到swash.exe的同一目录下。并在这个目录下，用如下指令运行：

swashrun l41ber01

运行完成后，得到6个结果数据文件 sect[N].tbl，其中N=1~8。
通过脚本mkplot.m将结果数据绘制成点线图。matlab脚本文件也在压缩包中。同时，mkplot.m实现了数据的可视化，于是得到 berkhoff_1.png 文件（图片如下）。

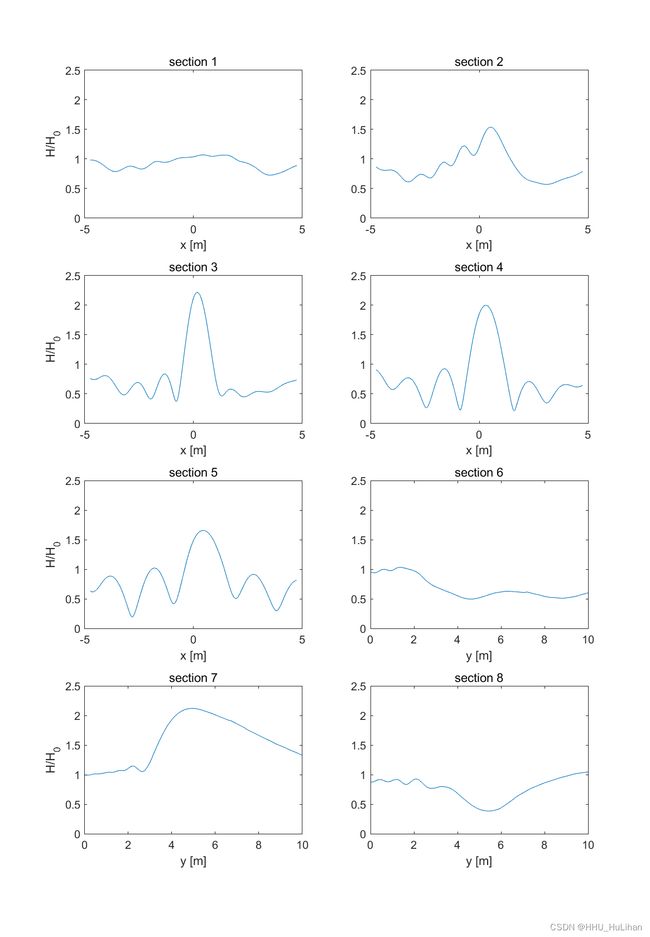
实验数据也附在压缩包的berkhoff_output.gif中，图中的红色圆圈即物理实验数据点。berkhoff_output.gif同时也是论文所示的模拟结果与物理实验结果的对比图（如下）。

---

1. https://doi.org/10.1016/j.coastaleng.2011.05.015 ↩︎

2. https://doi.org/10.1016/j.compfluid.2020.104751 ↩︎

3. https://doi.org/10.1002/fld.595 ↩︎ ↩︎

4. https://doi.org/10.1016/0378-3839(82)90022-9 ↩︎