深度学习修炼（一）线性分类器 | 权值理解、支撑向量机损失、梯度下降算法通俗理解

如图是神经网络训练的一般过程总结图
今天从线性分类器开始

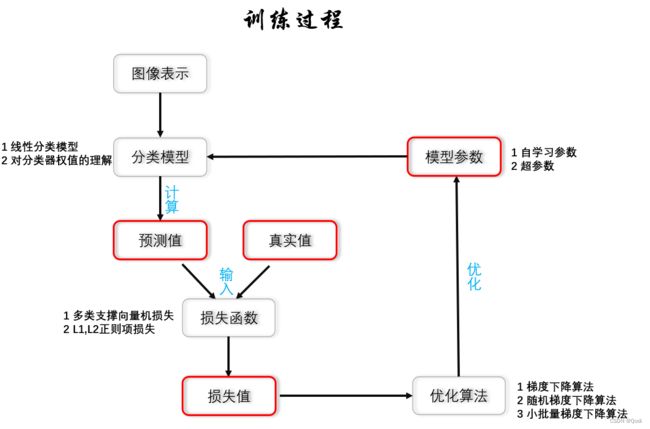
为什么我们从线性分类器开始?是由于线性分类器的基本特点决定的

1 基本特点

​ 形式简单、易于理解，通过层级结构（神经网路）或者高维映射（支撑向量机）可以形成功能强大的非线性模型。
从某种意义上来说，未来的卷积网络以及更为复杂的网络都离不开线性分类器

​ 线性分类器是一种线性映射，将输入的图像特征映射为类别分数

2 训练过程

2.1 图像预处理

​ 比如张CIFAR10 中每一张图像像素为32×32 ，每一个（采用RGB）像素通道为3，我们首先要将图片转换为一个向量，转换方式多种，现在我们只做简单的转换方式，用一个32×32×3=3072维的列向量来表示我们这张图片。

2.2 线性分类器构造

​ $f_i(x,w_i)=w_i^{T}x+b_i$ $i=1,...,c$

• x代表输入的d维图像向量 这个例子是3072维度的向量
• $w_i=[w_{i1},...,w_{id}{]}^T$为第i个类别的权值向量，行数由类别数决定，如以上例子有10类，列数由输入的x向量的维度决定，如以上例子为3072维 因而$w_i$的维度为10×3072
• $b_i$为偏置值。

当我们把一张图片（转换为3072×1的向量），输入到这个式子中，得到每个类下这张图片的分数（10×1的列向量），分数越高，是该类别的可能性就越大

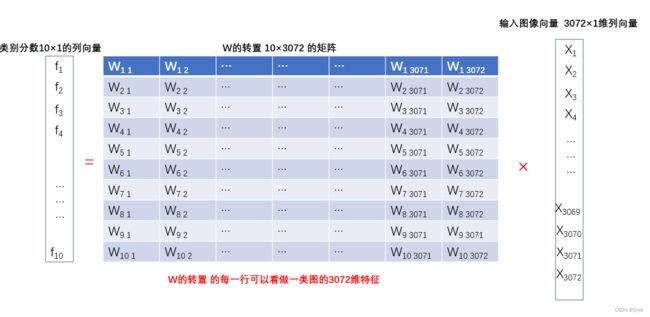
然后我们就需要让模型不断优化这些参数，使得最后正确的类别的分数尽可能高
在线性模型的例子中，我们本质学习到什么？就是上图的这个W矩阵 ! 也就是分类器的权值，优化模型也就是优化这里的权值
那边该怎么理解这个权值呢？

2.2.1多角度理解我们分类器的权值W

理解线性分类器的角度一

线性分类器的w权值信息，其实就是训练样本的平均值，统计信息，是每一类别的一个模板。由于W也是3072维的，因而我们可以进行权值模板的可视化

我们可以把它显示为32×32×3的图片，这时候就会得到10张图片，对应10类，我们实际上是将权值W可视化，观察我们可以发现：每一类其实就是该类下各个图片的一个均值，一个统计信息，如果我们新输入的图片和某一类模板相似，就会导致该类模板对应的额分数更高。

比如这里的W8代表马类，观察到两个马头，一个朝左，一个朝右，为什么呢？因为训练样本中就有的马头朝左，有的马头朝右

理解线性分类器权值角度二

如图，我们实际上就是要找一些分界面，来把不同类比的分开，如下面的红蓝绿线

• 我们距离线越远，他的得分越高，也就意味着相应的类别特征越明显
• 距离线越近，得分越低，也就类别特征越模糊

分数等于0的相当于一个决策面 分界面。

w控制着线的方向，b控制着分界面的偏移

但是真实世界中的数据集往往都不是线性可以分开的，线性网络表现会很差
所以在此基础上有很多非线性操作进行改进，如多层感知机，卷积等

2.3 损失函数计算损失值

我们要优化模型参数，就离不开损失函数的帮助

2.3.1 损失函数定义

什么是损失函数呢？

比如我们的真实值是猫咪，设有两组权值他们对于猫咪的预测的分数都是最高的，但我们权值一预测猫咪的分数是900分，权值二预测的分数是100分，很明显权值一更好，因而我们就是通过损失函数来定量的展现这样的差异。

它搭建了模型性能与模型参数之间的桥梁，指导模型参数的优化，

它其实是预测值与真实值的不一致程度，量化了这个指标，我们把它称为损失值，损失值越大，不一致程度越大，也就预测的越不准确

我们的每一次学习结束后，都可以对应得到一些新的参数，我们检测新的参数的好坏。

可以拿一百张新的图像去测试，然后把每一张图片的测试结果都对应得到一个损失值，把这一百个损失值加起来除以测试总数一百，就得到我们平均的损失值。反映了这一组参数的整体的水平，抽象为数学表达式为

$L=\frac{1}{N}\sum (L_i)$

$L_i$为 单张图片的损失值

损失函数有很多，先举一个例子

2.3.2 损失举例：多类支撑向量机损失

单样本的多类支撑向量机损失

$L_i=\sum max(0,s_{ij}-s_{yi}+1)$

如何直观理解多类支撑向量机损失？

如果模型给 正确类别打的分数比给错误类别的分数高1分及以上，这时损失函数返回为0。
否则的话就是把模型给错误类别的分数加上1分减去我们正确类别的分数就是我们得到的损失值。
看个例子就明白了
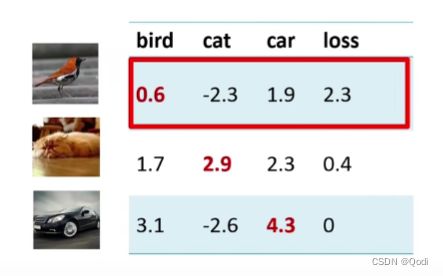
横行是模型给一张图的类别判断，分越高，模型觉得图形是哪一类

如上

• 第一行的正确类为鸟类，模型给错误类猫类分数比鸟类分数高2.9 超过一分，该项损失值为0，但对于汽车类模型没有高超过一分（反而低），因而错误的汽车类分数+1得到2.9再减去正确类鸟类的分数0.6等于2.3 1.9+1-0.6=2.3 总损失0+2.3=2.3
• 第二行的正确类为猫类，比错误类鸟类分数高超过一分，该项损失值为0，但对于汽车类没有高超过一分，因而错误的汽车类分数+1得到3.3再减去正确类猫类的分数2.9等于0.4 2.3+1-2.9=0.4 总损失0+0.4=0.4
• 第三行的正确类为汽车类，比其他错误类的分数都大于一分，因而总损失为零

2.3.3 优化损失函数

即便有了损失值，有时候我们也会出现损失值一模一样的情况，这时候如何评定参数好坏呢？就是通过添加包含超参数正则项损失 其中$\lambda$ 是超参数（超参数 不通过学习设置的参数，预先人为设定好的参数）这个超参数的作用是控制着正则项损失在总损失中占得比重

• $\lambda$为0的时候只依靠前面的损失函数
• $\lambda$为无穷的时候仅考虑正则项损失

$L=\frac{1}{N}\sum (L_i)+\lambda R(W)$

正则项具体可以分为：

​ L1 正则项 把权值矩阵W的每个元素取绝对值后再相加

​ L2 正则项 把权值矩阵W的每个元素先平方再相加

如何直观理解正则项

正则项对于大数权值进行惩罚，喜欢分散权值，鼓励分类器将所有维度的特征值用起来。而不是强烈的依赖其中少说的几维特征。防止模型训练的太好，过拟合（即只能学会自己的数据）。

使得每个维度的特征运用起来，有什么意义呢？

• 避免受到噪声影响，假设它强烈依赖某一维度，那么一但那一维度受到噪声污染，判断就会严重错误，而如果分散权值，那么即便某一维度受到影响，也不影响整体判断
• 还有避免模型产生偏好，对某一维度的特征喜欢，产生记忆，因而也就会产生过拟合，所以正则项的一个重要作用就是防止过拟合！！！

我们目前更多地是使用L2正则项，原因是计算方便

不过L1损失函数也有优点，就是L1对于异常值更不敏感，鲁棒性更强

2.4 优化算法

2.4.1 优化的定义？

是机器学习的核心步骤，利用函数的输出值作为反馈信号来调整分类器参数，以提升分类器对训练样本的预测性能。

实际上我们就是要找使得损失函数的值是最小的那一组参数！！！而我们对这类问题并不陌生，高中的时候学习导数的时候讲过求最值问题，实际上是要找一些导数为零的点，这些导数为零的点中就有我们的最小值点。

假如我们只有一个参数W,且损失函数是

$L=W^2+2W+1$

我们想要使得损失函数最小，我们可以很轻松知道是在W=-1的位置

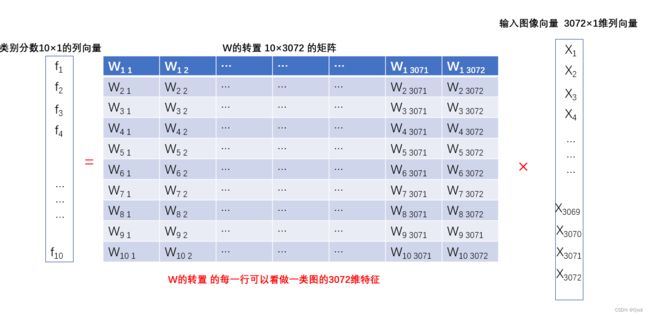
但是实际问题中，我们的损失函数L往往非常复杂，同时W也十分庞大，如下图一个简单的线性模型，他的要学习的W的参数量就达到了10*3072维=30720。直接求导数为零的点就会变得十分困难，所以我们通过梯度下降算法来使得损失减小。

2.4.2 梯度下降算法

​ 它是其中的一种简单而高效的优化算法

​ 设想我们被遮住了双眼，被困在一个寂静的山谷，我们只知道只能在山谷最低的地方才有机会存活下来。我们该怎么办

​ 唯一的办法是四处摸，找到向下的路，然后一点一点从高处移动到低处。

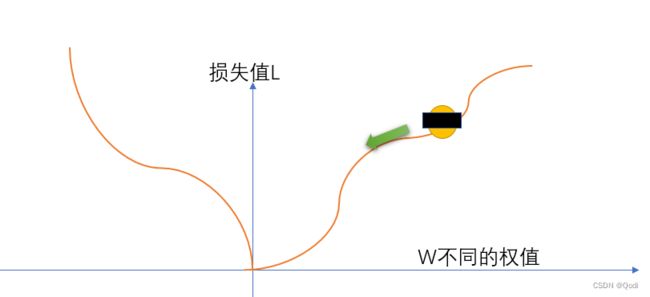
这 便是梯度下降算法的核心思想

我们需要把全部训练数据样本传入我们的分类器，这时候他就会根据我们的输出类别分数的好坏去调整参数W

相当于此时我们是$L(W{}_i)$ 自变量是W,因变量是损失值L

我们只需要解决两个问题

往哪走？

​ 负梯度方向，也就是向导数为负数且变化最快的点走，导数为负的点可以让函数值减小，也就是损失减小

走多远？

​ 步长（也就学习率）来决定，步长也是我们的认识到的第二个超参数

因而我们把问题由找到导数为零的点转换为求某一点的梯度，$\frac{\partial f}{\partial W_i}$进而来不断更新权值

权值的梯度 <=计算梯度（损失，训练样本，权值）

​ 权值 <=权值-学习率*权值的梯度

如何来求某一点的梯度呢？也就是在 一个已知一个权值矩阵的基础上如何确定他的梯度

1、 数值法

​ 也就是利用求导的定义式，所以求得的是一个近似值

​ 数值法求梯度主要用于检验解析梯度是否正确

2、 解析法

​ 求这一点的导数，然后代入这一点的值

​ 但这有一个问题，我们每次迭代计算都得把样本中的每一个数据都算一遍！当数据集样本足够大的时候，运算速度就会很慢，因而我们采用以下的方式改进

2.4.3 随机梯度下降算法

也就是我们这次不参考全部样本，而是从样本集合中随机抽取一个来更新。这样就会计算很多了，但是这样有一个问题，就是可能会抽取到噪声等一些不太好的样本，这时候会把我们带偏，但是这种方法依然可行，因为在大量抽样的情况下，整体还是向着梯度下降的方向去的。

2.4.4 小批量梯度下降算法

既然全部抽取速度太慢，部分抽取又可能会不稳定，那我们很容易想到取中间，也就是说我们随机抽取m个样本，计算损失并更新梯度。

这样的话我们计算效率会更高，同时也会更稳定！！！

梯度下降算法（Gradient Descent)的原理和实现步骤 - 知乎 (zhihu.com)

[梯度下降算法原理讲解——机器学习_zhangpaopao0609的博客-CSDN博客_梯度下降](