二叉树进阶练习
目录
一、根据二叉树创建字符串
二、二叉树的最近公共祖先
三、二叉搜索树与双向链表
四、从前序与中序遍历序列构造二叉树
五、从中序与后序遍历序列构造二叉树
六、二叉树的前序遍历(非递归实现)
七、二叉树的中序遍历(非递归实现)
八、二叉树的后序遍历(非递归实现)
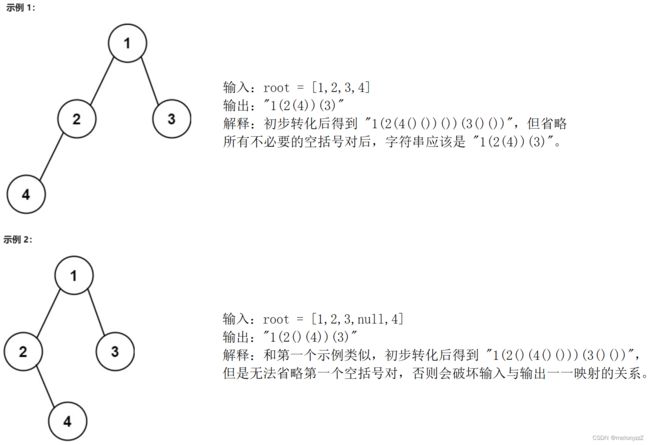
一、根据二叉树创建字符串
总结:
-
左、右子树都为空 --> 不递归遍历左、右子树
-
左子树为空,右子树不为空 --> 递归遍历左、右子树
-
左子树不为空,右子树为空 --> 只递归遍历左子树
-
左、右子树都不为空 --> 递归遍历左、右子树
即当左子树不为空或者右子树不为空时,递归遍历左子树;仅当右子树不为空时,才递归遍历右子树。
class Solution {
public:
string tree2str(TreeNode* root) {
if (root == nullptr)
return "";
string str = to_string(root->val);
// 当左子树不为空或者右子树不为空时,递归遍历左子树
if (root->left || root->right)
{
str += "(";
str += tree2str(root->left);
str += ")";
}
// 仅当右子树不为空时,才递归遍历右子树
if (root->right)
{
str += "(";
str += tree2str(root->right);
str += ")";
}
return str;
}
};二、二叉树的最近公共祖先
方法一:
因为一个节点也可以是它自己的祖先,所以首先判断当前根节点 root 是否等于节点 p 或 q,即判断 p 或 q 是否就是它们的最近公共祖先。
如果不是,则判断 p 和 q 是否分别在 root 的左、右子树中。对于一棵二叉搜索树,可以通过节点的值确定 p 和 q 是在 root 的左子树中,还是右子树中;但对于一棵普通二叉树,只能通过查找的方式确定。
-
如果 p 和 q 都在 root 的左子树中,则 p 和 q 的最近公共祖先应该在 root 的左子树中;
-
如果 p 和 q 都在 root 的右子树中,则 p 和 q 的最近公共祖先应该在 root 的右子树中;
-
如果 p 和 q 分别在 root 的左、右子树中,则 root 就是 p 和 q 的公共祖先。
class Solution {
public:
bool search(TreeNode* root, TreeNode* x) {
if (root == nullptr)
return false;
return root == x || search(root->left, x) || search(root->right, x);
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
if (root == p || root == q) // 一个节点也可以是它自己的祖先
return root;
bool pInLeft, pInRight, qInLeft, qInRight;
pInLeft = search(root->left, p);
pInRight = !pInLeft;
qInLeft = search(root->left, q);
qInRight = !qInLeft;
if (pInLeft && qInLeft)
return lowestCommonAncestor(root->left, p, q);
else if (pInRight && qInRight)
return lowestCommonAncestor(root->right, p, q);
else
return root;
}
};方法二:
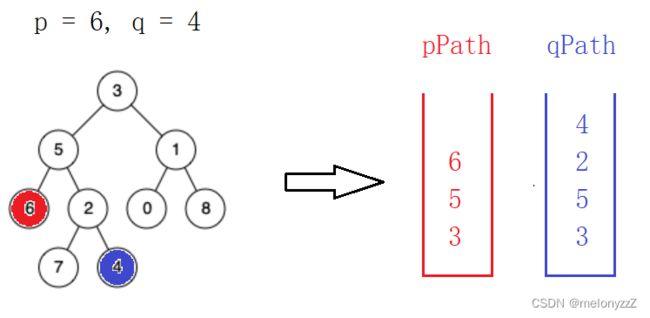
如果二叉树的存储结构为三叉链表,即节点结构中增加了一个指向其双亲结点的指针域,那么该问题就可以转化成 相交链表。
如果二叉树的存储结构为二叉链表,我们也可以沿着上述的思路解决该问题,例如:
class Solution {
public:
// 找到 root 到 x 的路径
bool FindPath(TreeNode* root, TreeNode* x, stack& path) {
if (root == nullptr)
return false;
path.push(root);
if (root == x)
return true;
if (FindPath(root->left, x, path))
return true;
if (FindPath(root->right, x, path))
return true;
path.pop();
return false;
}
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
stack pPath, qPath;
FindPath(root, p, pPath);
FindPath(root, q, qPath);
while (pPath.size() > qPath.size())
{
pPath.pop();
}
while (qPath.size() > pPath.size())
{
qPath.pop();
}
while (pPath.top() != qPath.top())
{
pPath.pop();
qPath.pop();
}
return pPath.top();
}
}; 三、二叉搜索树与双向链表
class Solution {
public:
void InOrder(TreeNode* cur, TreeNode*& prev) {
if (cur == nullptr)
return;
InOrder(cur->left, prev);
cur->left = prev;
if (prev)
prev->right = cur;
prev = cur;
InOrder(cur->right, prev);
}
TreeNode* Convert(TreeNode* pRootOfTree) {
if (pRootOfTree == nullptr)
return nullptr;
TreeNode* prev = nullptr;
InOrder(pRootOfTree, prev);
TreeNode* phead = pRootOfTree;
while (phead->left)
{
phead = phead->left;
}
return phead;
}
};四、从前序与中序遍历序列构造二叉树
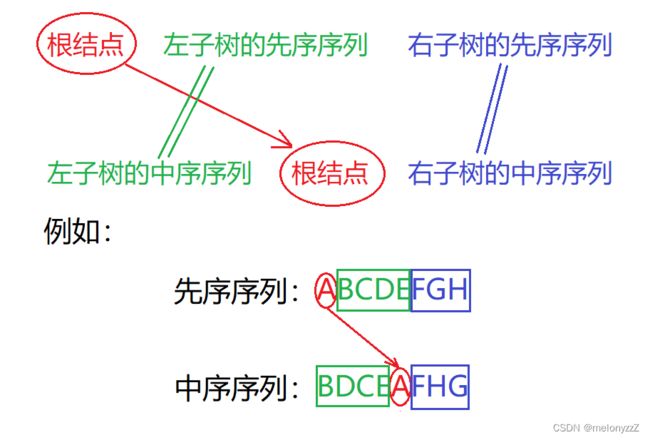
-
在先序序列中,第一个节点一定是二叉树的根节点。
-
根据根节点可以将中序序列分割成两个子序列,前一个子序列是根节点的左子树的中序序列,后一个子序列是根节点的右子树的中序序列。
-
根据这两个子序列,可以在先序序列中找到对应的左子序列和右子序列。在先序序列中,左子序列的第一个节点是左子树的根节点,右子序列的第一个根节点是右子树的根节点,这样就确定了二叉树的三个节点。同时,左子树和右子树的根节点又可以把左子序列和右子序列划分成两个子序列,如此递归下去,当取尽先序序列中的根节点时,便可得到一棵二叉树。
class Solution {
public:
TreeNode* _buildTree(vector& preorder, vector& inorder,
int L1, int R1, int L2, int R2)
{
// 先序序列的第一个节点一定是根节点
TreeNode* root = new TreeNode(preorder[L1]);
// 找到根节点在中序序列中的位置
int pos = L2;
while (pos <= R2)
{
if (preorder[L1] == inorder[pos])
break;
++pos;
}
// 判断左子树是否存在
if (pos > L2)
{
// 递归构造左子树
root->left = _buildTree(preorder, inorder,
L1 + 1, L1 + pos - L2, L2, pos - 1);
}
// 判断右子树是否存在
if (pos < R2)
{
// 递归构造右子树
root->right = _buildTree(preorder, inorder,
R1 - (R2 - pos) + 1, R1, pos + 1, R2);
}
return root;
}
TreeNode* buildTree(vector& preorder, vector& inorder)
{
return _buildTree(preorder, inorder,
0, preorder.size() - 1, 0, inorder.size() - 1);
}
}; 五、从中序与后序遍历序列构造二叉树
class Solution {
public:
TreeNode* _buildTree(vector& postorder, vector& inorder,
int L1, int R1, int L2, int R2)
{
// 后序序列的最后一个节点一定是根节点
TreeNode* root = new TreeNode(postorder[R1]);
// 找到根节点在中序序列中的位置
int pos = L2;
while (pos <= R2)
{
if (postorder[R1] == inorder[pos])
break;
++pos;
}
// 判断左子树是否存在
if (pos > L2)
{
// 递归构造左子树
root->left = _buildTree(postorder, inorder,
L1, L1 + pos - L2 - 1, L2, pos - 1);
}
// 判断右子树是否存在
if (pos < R2)
{
// 递归构造右子树
root->right = _buildTree(postorder, inorder,
R1 - (R2 - pos), R1 - 1, pos + 1, R2);
}
return root;
}
TreeNode* buildTree(vector& inorder, vector& postorder)
{
return _buildTree(postorder, inorder,
0, postorder.size() - 1, 0, inorder.size() - 1);
}
}; 六、二叉树的前序遍历(非递归实现)
class Solution {
public:
vector preorderTraversal(TreeNode* root) {
stack st;
TreeNode* cur = root;
vector v;
while (cur || !st.empty())
{
while (cur)
{
v.push_back(cur->val);
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
st.pop();
cur = top->right;
}
return v;
}
}; 七、二叉树的中序遍历(非递归实现)
class Solution {
public:
vector inorderTraversal(TreeNode* root) {
stack st;
TreeNode* cur = root;
vector v;
while (cur || !st.empty())
{
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
st.pop();
v.push_back(top->val);
cur = top->right;
}
return v;
}
}; 八、二叉树的后序遍历(非递归实现)
class Solution {
public:
vector postorderTraversal(TreeNode* root) {
stack st;
TreeNode* prev = nullptr;
TreeNode* cur = root;
vector v;
while (cur || !st.empty())
{
while (cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
// top 的右子树为空,或者
// 上一次访问完的节点是 top 的右子树的根节点,
// 说明 top 的右子树已经遍历过了
if (top->right == nullptr || top->right == prev)
{
st.pop();
v.push_back(top->val);
prev = top;
}
else
{
cur = top->right;
}
}
return v;
}
};