普通卷积、转置卷积详细介绍以及用法

1、普通卷积操作

首先回顾下普通卷积，下图以stride=1，padding=0，kernel_size=3为例，假设输入特征图大小是4x4的（假设输入输出都是单通道），通过卷积后得到的特征图大小为2x2。一般使用卷积的情况中，要么特征图变小（stride > 1），要么保持不变（stride = 1），当然也可以通过四周padding让特征图变大但没有意义

pytorch中的Tensor通道排列顺序是：[batch, channel, height, width]
卷积（Conv2d）在pytorch中对应的函数是：

torch.nn.Conv2d(in_channels, 
                out_channels, 
                kernel_size, 
                stride=1, 
                padding=0, 
                dilation=1, 
                groups=1, 
                bias=True, 
                padding_mode='zeros')

import torch.nn as nn
import torch
 
 
im = torch.randn(1, 1, 5, 5)
c = nn.Conv2d(1, 1, kernel_size=2, stride=2, padding=1)
output = c(im)
 
print(im)
print(output)
print(list(c.parameters()))

通过计算我们知道输出矩阵尺寸应该为N =（5 - 2 + 2*1）/ 2 +1 = 3.5，但实际的打印信息如下：

2、转置卷积

转置卷积（Transposed Convolution） 在语义分割或者对抗神经网络（GAN）中比较常见，其主要作用就是做上采样（UpSampling）。在有些地方转置卷积又被称作fractionally-strided convolution或者deconvolution，但deconvolution具有误导性，不建议使用。对于转置卷积需要注意的是：

• 转置卷积不是卷积的逆运算
• 置卷积也是卷积

转置卷积刚刚说了，主要作用就是起到上采样的作用。但转置卷积不是卷积的逆运算（一般卷积操作是不可逆的），它只能恢复到原来的大小（shape）数值与原来不同。转置卷积的运算步骤可以归为以下几步：


下图展示了转置卷积中不同s和p的情况：

s=1, p=0, k=3 ↑↑↑↑↑

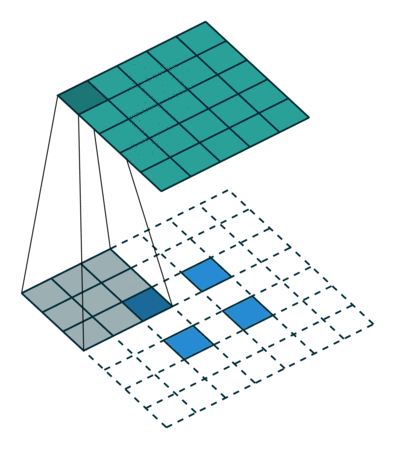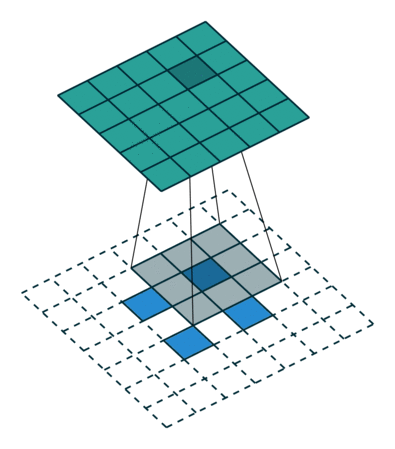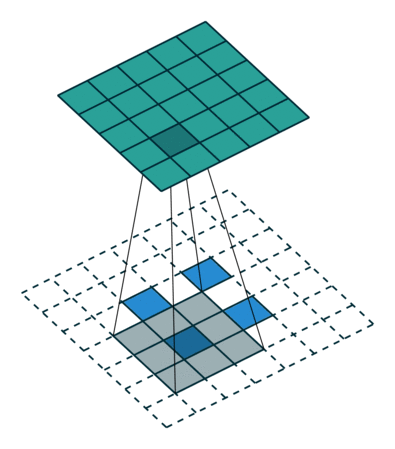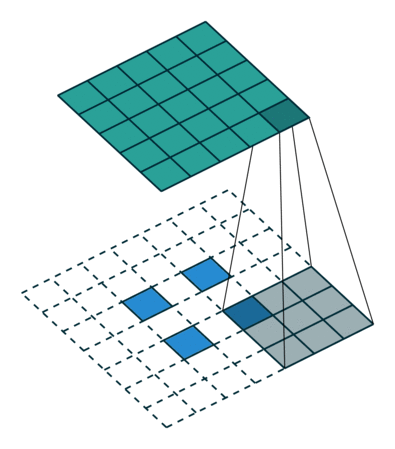
s=2, p=0, k=3 ↑↑↑↑↑

s=2, p=1, k=3 ↑↑↑↑↑
转置卷积操作后特征图的大小可以通过如下公式计算：

通过上面公式可以看出padding越大，输出的特征矩阵高、宽越小，可以理解为正向卷积过程中进行了padding然后得到了特征图，现在使用转置卷积还原到原来高、宽后要把之前的padding减掉

2.1 Pytorch转置卷积实验

下面使用Pytorch框架来模拟s=1, p=0, k=3的转置卷积操作：

import torch
import torch.nn as nn


def transposed_conv_official():
    feature_map = torch.as_tensor([[1, 0],
                                   [2, 1]], dtype=torch.float32).reshape([1, 1, 2, 2])
    print(feature_map)
    trans_conv = nn.ConvTranspose2d(in_channels=1, out_channels=1,
                                    kernel_size=3, stride=1, bias=False)
    trans_conv.load_state_dict({"weight": torch.as_tensor([[1, 0, 1],
                                                           [0, 1, 1],
                                                           [1, 0, 0]], dtype=torch.float32).reshape([1, 1, 3, 3])})
    print(trans_conv.weight)
    output = trans_conv(feature_map)
    print(output)


def transposed_conv_self():
	"""
	首先在元素间填充s-1=0行、列0（等于0不用填充）
	然后在特征图四周填充k-p-1=2行、列0
	接着对卷积核参数进行上下、左右翻转
	最后做正常卷积（填充0，步距1）
	"""
    feature_map = torch.as_tensor([[0, 0, 0, 0, 0, 0],
                                   [0, 0, 0, 0, 0, 0],
                                   [0, 0, 1, 0, 0, 0],
                                   [0, 0, 2, 1, 0, 0],
                                   [0, 0, 0, 0, 0, 0],
                                   [0, 0, 0, 0, 0, 0]], dtype=torch.float32).reshape([1, 1, 6, 6])
    print(feature_map)
    conv = nn.Conv2d(in_channels=1, out_channels=1,
                     kernel_size=3, stride=1, bias=False)
    conv.load_state_dict({"weight": torch.as_tensor([[0, 0, 1],
                                                     [1, 1, 0],
                                                     [1, 0, 1]], dtype=torch.float32).reshape([1, 1, 3, 3])})
    print(conv.weight)
    output = conv(feature_map)
    print(output)


def main():
    transposed_conv_official()
    print("---------------")
    transposed_conv_self()


if __name__ == '__main__':
    main()