【数据结构】B树的介绍及结点的插入删除

笔记是跟着B站王道考研的数据结构视频写的

B树

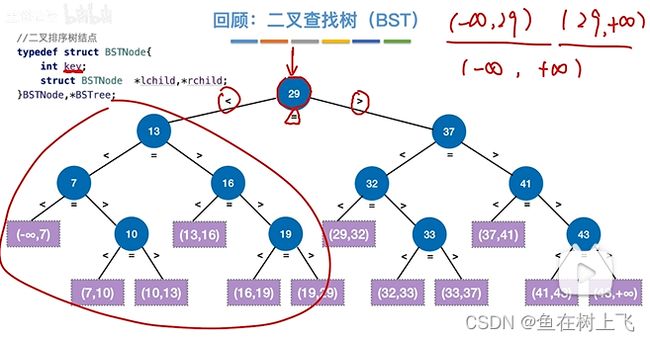
1. 二叉搜索树BST

二叉搜索树又称二叉排序树、二叉查找树，具有以下性质：

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值（没有等于，除非特殊说明，搜索树中不会有重复元素）
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

二叉搜索树的中序遍历结果是有序数组

2. 多叉查找树

struct Node{
	ElemType keys[4];//最多4个值，元素类型得一样
	struct Node* child[5];//最多5个指针
	int num;//这个比二叉树多一行，记录该节点具体有几个关键字，因为不一定是满的，比如头结点往往就1个值
};

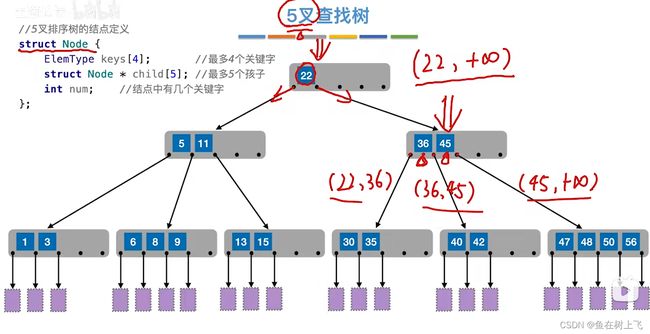
图中，紫色节点都是空结点，被称为“失败节点”（就是待查找的数值不在这棵树上，一直找到空结点了，查找失败，因此得名）
对m叉查找树，其每个节点上有m个指针，m - 1个值，查找的时候因为每个节点里面的数据是有序的，所以可以对每个节点里面也可以采用二分查找方法，尤其是m很大时，比如15叉，那一个节点里面有十四个关键字，就得用二分找的快了，这里举的例子因为不超过5，所以每个节点内部按照顺序查找方式

3. 5叉搜索树的退化

如果5叉搜索树没有规定每个节点最少有几个关键字，在整棵树的关键字总数一定时，每个节点上的关键字太少，那么需要的节点数也越多，树也越高，这样增加了查找的时间复杂度，如下图退化成了二叉查找树：

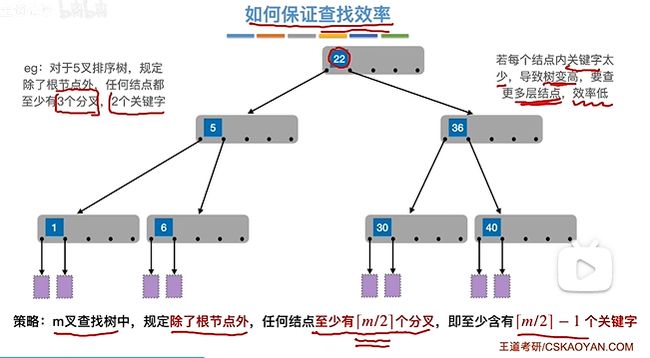
所以需要额外的规定，见上图的策略。

[m / 2]是m除以2然后向上取整，比如5叉查找树，每个节点至少有3个分叉，3 - 1 = 2个关键字

注意是除了根节点，因为如果一棵树只有一个值的话，那就只有两个分叉了，所以根节点除外（所以第二层一般就只有两个节点）

4. 平衡树

为了保证查找效率，还需要保证树的平衡，比如平衡二叉搜索树（Balanced Binary Tree），又叫AVL树（提出者的英文首字母）就是为了提高二叉搜索树的效率，它规定AVL树任何节点的两个子树的高度最大差别为1，此外，红黑树也是AVL树。

比如[1, 3, 5, 11, 22]要是以下列方式建5叉搜索树，显然查找效率太低了。按照AVL树的思维，应该以中间数值 5 作为根节点，这样左右就平衡了。

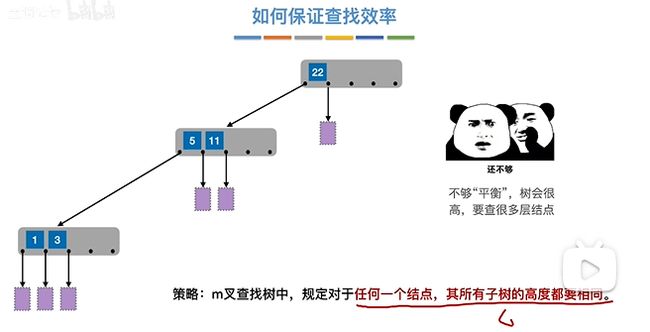
于是继续引入新规定，如图策略所示。这个策略比AVL树更严格，它要求所有子树的高度都要相同

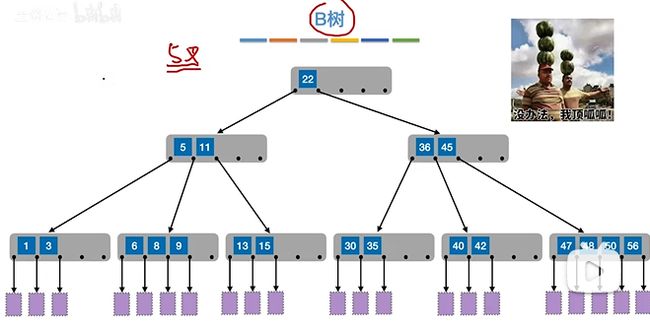
5. B树

当上面两个规定都满足时（一是为了保证树够低而对节点中关键字的数量和分叉数量的规定；二是为了保证树的平衡而对子树高度差作规定），其实就是一颗B树了。

尽管B树的提出者也没意思说明为什么叫B树，但是我们可以把它的B理解为Balance

上图是一个 5 阶B树（它的所有节点中，最多有5个分叉，比如上图右下方节点），根节点只有一个关键字

B树的完整定义：

王道这里把最底下的空结点（上图紫色）叫做叶子节点或失败节点，但我们一般算树的高度时不会算这些空的节点，因此我一般把含有数值的最底层节点叫做叶子节点，如上图1,3,6,8,9…，实际上王道在讲后面的B+树时就把最下面的非空节点成为叶子节点（即他们在不同树上对叶子节点的定义是不同的）

B树的高度：

问：含有n个关键字的m阶B树，最小高度和最大高度分别是多少？

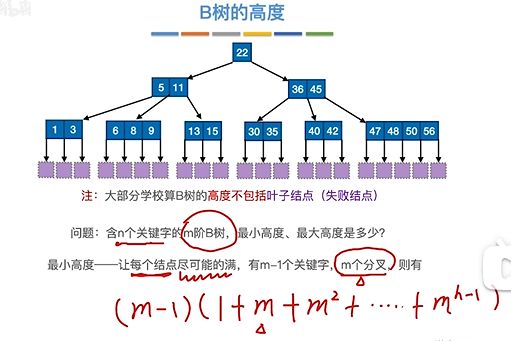
首先是最小高度：

想让高度最小，则每个节点里关键字越多越好，且分叉数越多越好。对于m阶B数，每个节点最多有 m - 1个关键字，最多有m个分叉，那么高度最小时设为h，总共的节点数就是（1 + m + m^2 + …+ m^h-1）,每个节点有m - 1个关键字，两个相乘即为关键字总数n.

等比数列求和公式s = a1(1 - q^n) / (1 -q)，可算得

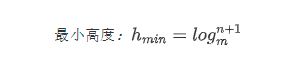
最大高度

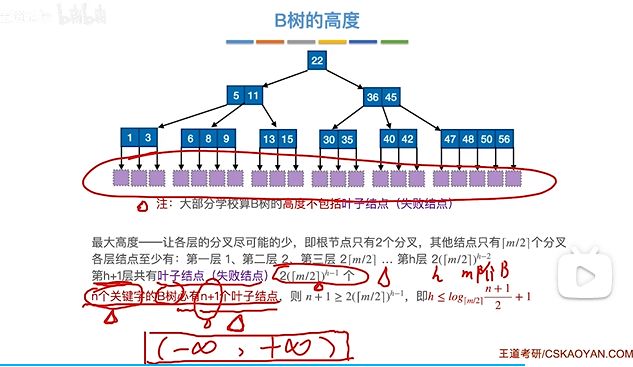
高度最大就是让分叉尽可能少，但除了根节点，不能低于[m / 2]，所以第h层的节点数如图所示。

因为n个关键字的B树最多有n + 1个失败节点。这句话可以这样理解，在B树中，n个关键字把负无穷到正无穷的区间分成了n + 1个区间，而失败的情况（最底下的空节点数，即失败节点总数）也是n + 1。

而在高度最大情况下，失败节点总数的计算即是h + 1层的节点数，也就是图中的 2([m/2]^h+1)，另n + 1和它相等，就能得到最大高度。

当然，如果关键字全是整数，而B树的最底层又有连续的，比如[1, 2, 3]那也只能分出负无穷到1、3到正无穷两个区间而不是4个区间，所以失败节点最多是n + 1个。

B树的插入和删除

插入和删除都是对一个数，即一个关键字，而不是整个节点，除非单个节点超出4个关键字时，就需要新建节点

1. 插入的话，是从底向上逐渐建树的，以5阶B树为例
   
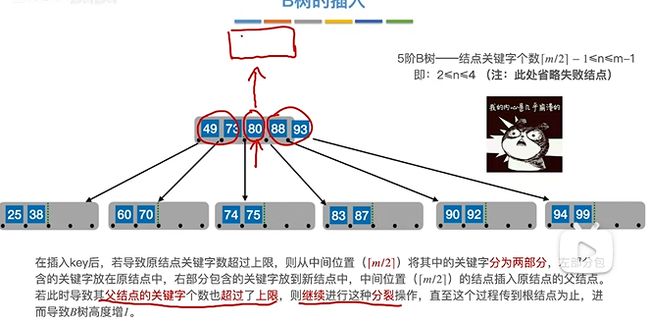
   当节点里关键字数量超出 5 - 1，即4个时，就把中间关键字向上提，
   
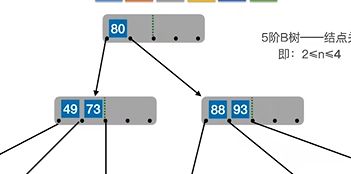
   注意每个节点的关键字在[2, 4]之间——[ ([m/2] - 1), (m - 1) ],m为5，除了根节点。

插入节点的总结：

2. 删除

首先是对非终端节点（即不是最底层的节点）

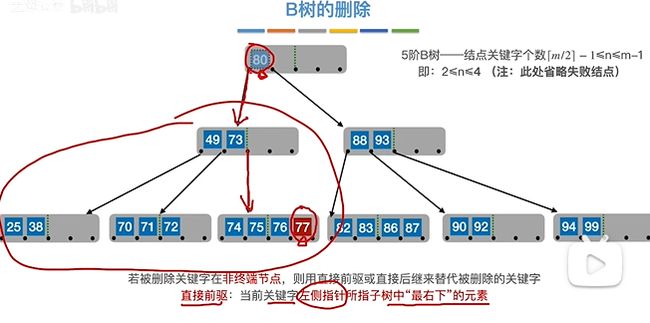
删除80后用直接前驱77替代（其实也能用82替代，即直接后继）：

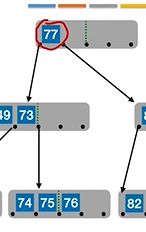
再删除77：

用直接后继82去替代（其实也能用直接前驱76替代，一样的）

所以，对非终端节点关键字的删除操作可以转化为对终端节点关键字的删除

但是删完后关键字数少于2的情况呢？

（1）当左右兄弟节点宽裕（移掉一个仍然满足关键字数量大于等于2，注意分叉数是m除以2向上取整，关键字子树是在此基础上-1），就将上一层父节点关键字替换被删节点，让兄弟节点的关键字去替换父节点移走的

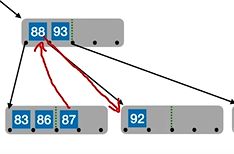
这里，删除92，就把88替换上去，再把87补在88原来的位置上。

在变换过程前后，要保证B树的特性没变，尤其是左子树上所有值<当前关键字<右子树上所有值

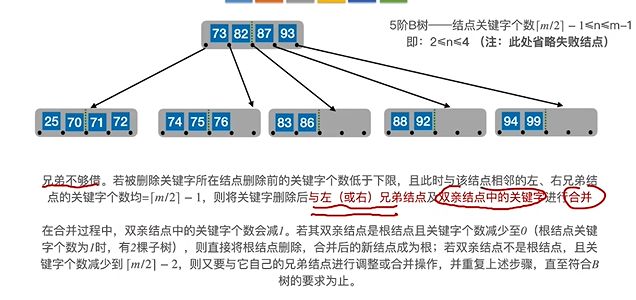
（2）当左右兄弟不宽裕时，需要将左右及其父节点合并：

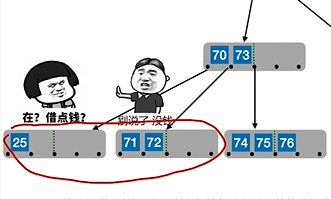
如图要删除25，但是右边也不够借，就把25, 70, 71, 72合并在一块

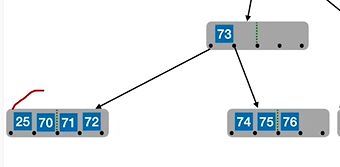
但73显然又不合法，没有大于等于2，就把73和旁边的兄弟节点、及父节点合并

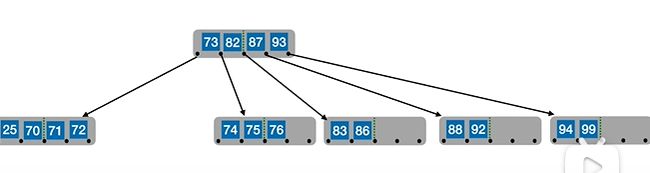
此时根节点为空了，然后删去根节点

删除节点的总结：