深入理解数据结构

数据结构

前言

• 大家好：我是一名有N年java开发经验的“猿”，在工作多年后怀揣着对技术的爱好决定探索计算机底层，学习数据结构并记录下来，在此与大家分享。在工作中虽然学会了java ，python，HTML/CSS/JS/ES6 等多种编程语言，但是缺乏对底层存储与实现的知识，本文主要用c语言实现各种数据结构，读者如果不了解c可以简单看一下c的菜鸟教程学习一下基本语法，用vscode可以很快的实现一个简单的demo，先分享下我的学习过程，首先我读了一遍，《数据结构 使用c语言（第五版）》的书，收获不是很大，然后读了一本《深入理解计算机系统》这本书内容对我启发很大，在读完这本书后再去看数据结构已经没有那么难了。希望这些可以带给大家帮助，学无止境，感谢前辈写的各种书籍供我们参考。

1. 数据结构(data structure)是带有结构特性的数据元素的集合，它研究的是数据的逻辑结构和数据的物理结构以及它们之间的相互关系，并对这种结构定义相适应的运算，设计出相应的算法，并确保经过这些运算以后所得到的新结构仍保持原来的结构类型。简而言之，数据结构是相互之间存在一种或多种特定关系的数据元素的集合，即带“结构”的数据元素的集合。“结构”就是指数据元素之间存在的关系，分为逻辑结构和存储结构。

2. 数据的逻辑结构和物理结构是数据结构的两个密切相关的方面，同一逻辑结构可以对应不同的存储结构。算法的设计取决于数据的逻辑结构，而算法的实现依赖于指定的存储结构。

3. 数据结构的研究内容是构造复杂软件系统的基础，它的核心技术是分解与抽象。通过分解可以划分出数据的3个层次；再通过抽象，舍弃数据元素的具体内容，就得到逻辑结构。类似地，通过分解将处理要求划分成各种功能，再通过抽象舍弃实现细节，就得到运算的定义。上述两个方面的结合可以将问题变换为数据结构。这是一个从具体（即具体问题）到抽象（即数据结构）的过程。然后，通过增加对实现细节的考虑进一步得到存储结构和实现运算，从而完成设计任务。这是一个从抽象（即数据结构）到具体（即具体实现）的过程。

4. 数据的逻辑结构：
   数据元素之间的相互联系方式称为数据的逻辑结构。
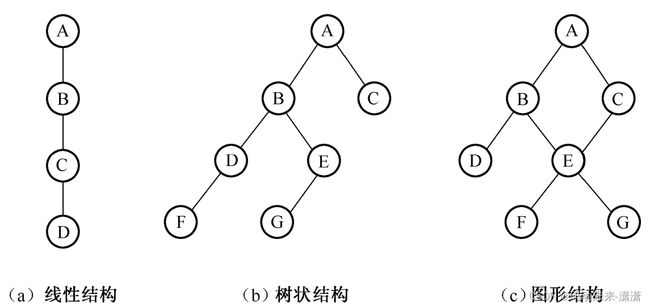
   按照数据元素之间的相互联系方式，数据的逻辑结构主要可分为线性结构、树状结构和图形结构三种。

线性结构的定义是： 除第一个和最后一个数据元素外，每个数据元素只有一个唯一的前驱数据元素和一个唯一的后继数据元素。线性结构可以表示为如图1-1（a）所示的形式，图中，A、B、C、D为数据元素，A是第一个数据元素，D是最后一个数据元素，A是B的前驱数据元素，C是B的后继数据元素；依次类推。
树状结构的定义是： 除根结点外，每个数据元素只有一个唯一的前驱数据元素，可有零个或若干个后继数据元素。图1-1（b）是一个树状结构的例子。对于数据元素A、B、C、D、E、F、G，数据元素A是根结点，A没有前驱数据元素，有两个后继数据元素B和C；数据元素B的前驱数据元素为A，后继数据元素为D和E；数据元素C的前驱数据元素为A，没有后继数据元素；
图形结构的定义是： 每个数据元素可有零个或若干个前驱数据元素和零个或若干个后继数据元素。图1-1（c）是一个图形结构的例子。对于数据元素A、B、C、D、E、F、G，若以A为起始点，则数据元素E有两个前驱数据元素B和C，有两个后继数据元素F和G。
树状结构和图形结构也可以归为非线性结构。数据元素之间不存在如图1-1（a）所示的一对一关系的结构都称为非线性结构。

5. 数据的存储结构：
   数据的存储结构是指数据的逻辑结构在计算机中的表示（又称映像，顺序印象和非顺序映像），数据元素之间的关系有两种不同的表示方法：顺序映象和非顺序映象，并由此得到两种不同的存储结构：顺序存储结构和链式存储结构

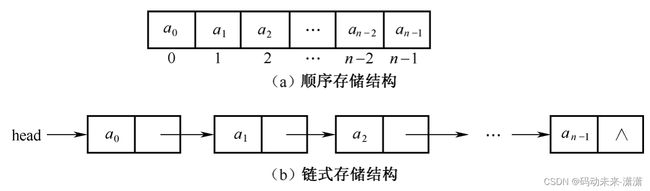
顺序存储结构: 是指把数据元素存储在一块连续地址空间的内存中。其特点是，逻辑上相邻的数据元素在物理上也相邻，数据间的逻辑关系表现在数据元素的存储位置关系上。当采用高级程序设计语言表示时，实现顺序存储结构的方法是使用数组。如图 1-2（a）所示为线性结构数据元素a0，a1，…，an-1的顺序存储结构示意图。其中，0，1，2，…，n-2，n-1既是数据元素的编号，也是存储数据元素a0，a1，…，an-1的数组下标。
//=============================================================
链式存储结构: 使用指针把相互直接关联的结点（即直接前驱结点或直接后继结点）链接起来。其特点是，逻辑上相邻的数据元素在物理上（即内存存储位置上）不一定相邻，数据间的逻辑关系表现在结点的链接关系上。如图1-2（b）所示为线性结构数据元素a0，a1，…，an-1的链式存储结构示意图。其中，上一个结点到下一个结点的箭头表示上一个结点的指针域中保存的下一个结点在内存中的存储地址。head是指向第一个结点的指针，通常称为头指针。

1. 数据的逻辑结构

1.1 线性结构

1.1.1 线性表

1. 定义： 线性结构的特点是，除第一个和最后一个数据元素外，每个数据元素只有一个前驱数据元素和一个后继数据元素。线性表是一种可以在任意位置进行插入和删除数据元素操作的、由 n（n≥0）个相同类型数据元素a0，a1，a2，…，an-1组成的线性结构。线性表是一种最简单的线性结构。

1.1.2 顺序表

1. 顺序表的存储结构
        当采用像C语言这样的高级程序设计语言描述数据结构问题时，实现顺序存储结构的方法是使用数组。数组把线性表的数据元素存储在一块连续地址空间的内存单元中，这样，线性表中逻辑上相邻的数据元素在物理存储地址上也相邻。数据元素间逻辑上的前驱、后继逻辑关系就表现在数据元素存储单元的物理前后位置关系上。
        数组有静态数组和动态数组两种。静态数组存储空间的申请和释放由系统自动完成，动态数组存储空间的申请和释放由用户通过调用系统函数自己完成。不论静态数组还是动态数组，其功能都是向系统申请一块地址连续的有限空间，只是申请空间的方法不同。
2. 顺序表的操作实现

// int_SeqList.h
#ifndef STUDY_C_202203_INT_SEQLIST_H
#define STUDY_C_202203_INT_SEQLIST_H


#define MaxSize 100
typedef int Int_DataType;
typedef struct INT_List
{
    Int_DataType list[MaxSize];
    int size;
} SeqList_int;
/**
 * 初始化
 * @param list
 */
void int_list_init(SeqList_int *list);
/**
 * 获取长度
 * @param list
 * @return
 */
int int_list_length(SeqList_int list);
/**
 * 新增数据
 * @param list 数据集合
 * @param i 下标
 * @param x data
 * @return
 */
int int_list_insert(SeqList_int *list, int i, Int_DataType x);
/**
 * 删除数据
 * @param list 数据集合
 * @param i 下标
 * @param x 删除的数据
 * @return
 */
int int_list_delete(SeqList_int *list , int i, Int_DataType *x);
/**
 * 获取下标为i位置的数据
 * @param L 数据集合
 * @param i 下标
 * @param x 返回的数据
 * @return
 */
int int_list_get(SeqList_int L, int i, Int_DataType *x);

#endif //STUDY_C_202203_INT_SEQLIST_H

// int_SeqList.c
#ifndef STUDY_C_202203_INT_SEQLIST_C
#define STUDY_C_202203_INT_SEQLIST_C


#include 
#include "int_SeqList.h"

void int_list_init(SeqList_int *list){
    list->size = 0;
}

int int_list_length(SeqList_int list)
{
    return list.size;
}

int int_list_insert(SeqList_int *list, int i, Int_DataType x)
{
    int j;
    if( list->size >= MaxSize)
    {
        printf("数组已满，无法插入\n");
        return 0;
    }
    else if(i < 0 || i > list->size)
    {
        printf("参数不合法! \n");
        return 0;
    }
    else{
        for (j = list->size; j >i ; j--) {
            list->list[j] = list->list[j-1];
        }
        list->list[i] = x;
        list->size++;
        return 1;
    }

}
int int_list_delete(SeqList_int *list , int i, Int_DataType *x)
{
    int j;
    if(list->size <= 0){
        printf("顺序表已空, 无数据可删\n");
        return 0;
    }
    else if (i < 0 || i > list->size - 1){
        printf("参数不合法");
        return 0;
    }else{
        *x = list->list[i];
        for (j = i+1; j <= list->size-1 ; j++) {
            list->list[j-1] = list->list[j];
        }
        list->size--;
        return 1;
    }
}

int int_list_get(SeqList_int L, int i, Int_DataType *x)
{
    if(i < 0 || i > L.size-1){
        printf("参数不合法");
        return 0;
    }
    else{
        *x = L.list[i];
        return 1;
    }
}
#endif //STUDY_C_202203_INT_SEQLIST_C

// main.c

#include "linear_struct/array/int_SeqList.h"

void test_array(){
    SeqList_int list;
    int i,x;
    int_list_init(&list);
    for (i = 0; i < 10; i++) {
        int_list_insert(&list,i,i+1);
    }
    int_list_delete(&list,5,&x); // 删除函数
    printf("%d --- \n",x);
    // 显示顺序表的当前数据元素
    for (i = 0; i < int_list_length(list); i++) {
        int_list_get(list,i,&x);
        printf("%d ### \n",x);
    }
}

int main() {
    test_array();
    return 0;
}

1.1.3 单向链表

1. 单链表定义

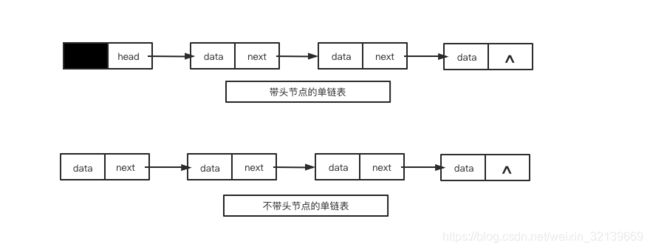
     单链表是一种链式存取的数据结构，用一组地址任意的存储单元存放线性表中的数据元素。链表中的数据是以结点来表示的，每个结点的构成：元素(数据元素的映象) + 指针(指示后继元素存储位置)，元素就是存储数据的存储单元，指针就是连接每个结点的地址数据。单链表中，构成链表的结点只有一个指向直接后继结点的指针域。

2. 单链表操作实现

// LinkedList.h
#ifndef STUDY_C_202203_LINKEDLIST_H
#define STUDY_C_202203_LINKEDLIST_H

typedef int l_DataType;

// 单向链表
typedef struct Node
{
    l_DataType data;
    struct Node *next;
} SLNode;
// 带头节点的链表
typedef struct Linked{
    struct Node *head;
    int size;
} LinkedList;

void LinkedListInit(LinkedList **linked);

/**
 * 返回链表长度
 * @param linked
 * @return
 */
int length(LinkedList *linked);

/**
 * 在第index位置插入数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
int l_insert_index(LinkedList **linked, int i, l_DataType x);

/**
 * 删除删除指定下标的数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
int l_del_index(LinkedList **linked, int i, l_DataType *x);

/**
 * 获取指定下标的数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
int l_get_index(LinkedList **linked, int i, l_DataType *x);

/**
 * 回收数据
 * @param linked
 */
void l_des(LinkedList **linked);

#endif //STUDY_C_202203_LINKEDLIST_H

// LinkedList.h
#ifndef STUDY_C_202203_LINKEDLIST_C
#define STUDY_C_202203_LINKEDLIST_C

#include 
#include 
#include "LinkedList.h"
/**
 * 初始化函数实现
 * @param linked
 */
void LinkedListInit(LinkedList **linked) {
    *linked = malloc(sizeof(LinkedList));               //初始化LinkedList结构体，申请空间
    (*linked)->head = (SLNode*)malloc(sizeof(SLNode));  //初始化head节点，分配空间
    (*linked)->size = 0;                                //初始化原素个数
}
int length(LinkedList *linked){
    return linked->size;
}
/**
 * 在第index位置插入数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
int l_insert_index(LinkedList **linked, int i, l_DataType x)
// 在带头结点单链表head的第i（0<=i<=size）个结点前插入一个存放数据元素x的结点
// 插入成功则返回1，失败则返回0
{
    SLNode *p,*q; // p 第index位置的指针
                  // q 新增的指针
    int j; //
    LinkedList *L= (*linked);
    p = L->head;
    j = -1;
    while(p->next != NULL && j < i - 1 ){
        // 最终让指针p指向第i-1个结点
        p = p->next;
        j++;
    }
    if(j != i-1){
        printf("元素参数错误");
        return 0;
    }
    q = (SLNode *) malloc(sizeof(SLNode)); // 新建结点
    q->data = x;    // 将值赋予data
    q->next = p->next; // 将index的位置的下一个指针赋予新增结点，
    p->next = q; // 将新增结点的指针赋予index位置的下一个指针，即与链表建立连接关系
    L->size++;
    return 1;
}

int l_del_index(LinkedList **linked, int i, l_DataType *x)
{
    SLNode *p,*del; // p 第index位置的指针
    // q 新增的指s
    int j; //
    LinkedList *L= (*linked);
    p = L->head;
    j = -1;
    while(p->next != NULL
        && p->next->next != NULL
        && j < i - 1 ){
        // 最终让指针p指向第i-1个结点
        p = p->next;
        j++;
    }
    if(j != i-1){
        printf("元素参数错误");
        return 0;
    }
    del = p->next; // 指针 del 指向 第index个结点
    *x = del->data; // 把指针 del 所指结点域值赋予x
    p->next = p->next->next; // 删除index位置的结点
    free(del); // 回收内存
    L->size--;
    return 1;
}
int l_get_index(LinkedList **linked, int i, l_DataType *x)
{
    SLNode *p;
    // q 新增的指s
    int j; // 临时变量
    LinkedList *L= (*linked);
    p = L->head;
    j = -1;
    while(p->next != NULL
          && j < i  ){
        // 最终让指针p指向第i-1个结点
        p = p->next;
        j++;
    }
    if(j != i){
        printf("元素参数错误");
        return 0;
    }
    *x = p->data;
    return 1;
}

void l_des(LinkedList **linked){
    SLNode *p,*cur;
    LinkedList *L= *linked;
    p = L->head;
    while(p != NULL){
        cur = p;
        p = p->next;
        free(cur);
    }
    L->head = NULL;
    free(*linked);
}

#endif //STUDY_C_202203_LINKEDLIST_C

// main.c
#include "linear_struct/linked/LinkedList.h"
void test_one_linked(){
    LinkedList *linkedList ;
    int i,x;
    LinkedListInit(&linkedList);
    for (i = 0; i < 10;i++) {
        l_insert_index(&linkedList,i,i+1);
    }
    l_del_index(&linkedList,6,&x);
    for (i = 0; i < length(linkedList); i++) {
        l_get_index(&linkedList,i,&x);
        printf("%d \n",x);
    }
    l_des(&linkedList);
}

int main() {
    test_one_linked();
    return 0;
}

1.1.4 双向链表

1. 双向链表定义

     双向链表也叫双链表，是链表的一种，它的每个数据结点中都有两个指针，分别指向直接后继和直接前驱。所以，从双向链表中的任意一个结点开始，都可以很方便地访问它的前驱结点和后继结点。

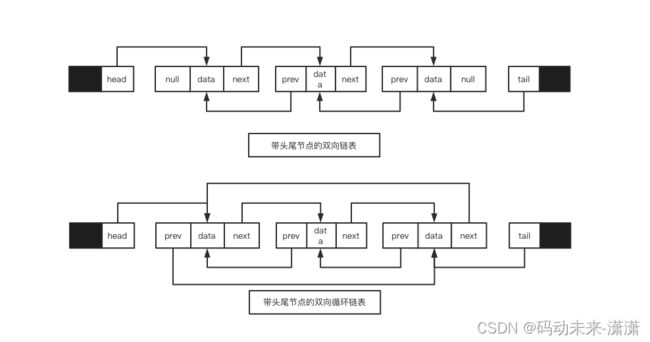
2. 双向链表操作实现

// LinkedList2.h 
#ifndef STUDY_C_202203_LINKEDLIST2_H
#define STUDY_C_202203_LINKEDLIST2_H

#include 
typedef int L2_DataType;

typedef struct Node2{
    struct Node2 *prev;//前驱结点
    L2_DataType data;
    struct Node2 *next;//后继结点
} Node2;
// 双向循环链表
typedef struct Linked2{
    struct Node2 *head;
    struct Node2 *tail;
    int size;
} LinkedList2;

void l2_LinkedListInit(LinkedList2 **linked);

/**
 * 返回链表长度
 * @param linked
 * @return
 */
int l2_length(LinkedList2 *linked);

/**
 * 在第index位置插入数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
bool l2_insert_index(LinkedList2 **linked, int i, L2_DataType x);

/**
 * 头部插入
 * @param linked
 * @param x
 * @return
 */
bool addHead(LinkedList2 **linked,L2_DataType x);

/**
 * 尾部插入
 * @param linked
 * @param x
 * @return
 */
bool addTail(LinkedList2 **linked,L2_DataType x);

/**
 * 移除数据
 * @param linked
 * @return
 */
int l2_del(LinkedList2 **linked);

/**
 * 删除删除指定下标的数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
int l2_del_index(LinkedList2 **linked, int i);

/**
 * 删除第一个结点
 * @param linked
 * @return
 */
int l2_del_first(LinkedList2 **linked);

/**
 * 删除最后一个结点
 * @param linked
 * @return
 */
int l2_del_last(LinkedList2 **linked);

/**
 * 获取指定下标的数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
int l2_get_index(LinkedList2 **linked, int i);

/**
 * 回收数据
 * @param linked
 */
void l2_des(LinkedList2 **linked);

/**
 * 头部插入
 * @param linked
 * @param x
 * @return
 */
bool addHead(LinkedList2 **linked,L2_DataType x);

/**
 * 尾部插入
 * @param linked
 * @param x
 * @return
 */
bool addTail(LinkedList2 **linked,L2_DataType x);

/**
 * 创建新结点
 * @param data
 * @param prev
 * @param next
 * @return
 */
Node2* createNode(L2_DataType data,Node2* prev,Node2* next);

// 插入数据异常检查
static bool checkPositionIndex(int size,int index);

/**
 * 任意位置插入结点
 * @param linked
 * @param index
 * @return
 */
Node2* node(LinkedList2 *linked,int index);

/**
 * 尾部插入
 * @param linked
 * @param e
 */
void linkLast(LinkedList2 **linked,L2_DataType e);

/**
 * 头部插入
 * @param linked
 * @param e
 */
void linkFirst(LinkedList2 **linked,L2_DataType e);

/**
 * 任意下标位置插入
 * @param linked
 * @param e
 * @param succ
 */
void linkBefore(LinkedList2 **linked,L2_DataType e, Node2 *succ);

/**
 * 删除时判断下标
 * @param linked
 * @param index
 * @return
 */
bool checkElementIndex(LinkedList2 *linked,int index);

/**
 * 删除指定结点数据
 * @param linked
 * @param x
 * @return
 */
int unlink(LinkedList2 **linked,Node2* x);

int unlinkFirst(LinkedList2 **linked,Node2 *f);

int unlinkLast(LinkedList2 **linked,Node2 *f);

#endif //STUDY_C_202203_LINKEDLIST2_H

// LinkedList2.c
#ifndef STUDY_C_202203_LINKEDLIST2_C
#define STUDY_C_202203_LINKEDLIST2_C

#include 
#include 
#include "LinkedList2.h"

void l2_LinkedListInit(LinkedList2 **linked){
    *linked = (LinkedList2*)malloc(sizeof(LinkedList2));
    (*linked)->head = NULL;
    (*linked)->tail = NULL;
    (*linked)->size = 0;
}

/**
 * 返回链表长度
 * @param linked
 * @return
 */
int l2_length(LinkedList2 *linked){
    return linked->size;
}

/**
 * 在第index位置插入数据
 * @param linked
 * @param i
 * @param x
 * @return
 */
bool l2_insert_index(LinkedList2 **linked, int i, L2_DataType x){
    LinkedList2 *L = *linked;
    if( !checkPositionIndex(L->size,i)){
        return false;
    }
    if (i == L->size){
        linkLast(linked,x);
    } else {
        linkBefore(linked,x, node(L,i));
    }
    return true;
}

// 头部插入
bool addHead(LinkedList2 **linked,L2_DataType x){
    return l2_insert_index(linked,0,x);
}

// 尾部插入
bool addTail(LinkedList2 **linked,L2_DataType x){
    int index = (*linked)->size;
    return l2_insert_index(linked,index,x);
}

Node2* createNode(L2_DataType data,Node2* prev,Node2* next){
    Node2* newNode = (Node2*)malloc(sizeof(Node2));
    newNode->prev = prev;
    newNode->data = data;
    newNode->next = next;
    return newNode;
}

int l2_del(LinkedList2 **linked){
    return l2_del_first(linked);
}

int l2_del_index(LinkedList2 **linked, int i){
    if(!checkElementIndex(*linked,i)){
        return -1;
    }
    return unlink(linked,node(*linked,i));
}

int l2_del_first(LinkedList2 **linked){
    Node2 *head = (*linked)->head;
    return unlinkFirst(linked,head);
}

int l2_del_last(LinkedList2 **linked){
    Node2 *tail = (*linked)->tail;
    return unlinkLast(linked,tail);
}

int l2_get_index(LinkedList2 **linked, int i){
    if(!checkElementIndex(*linked,i)){
        return -1;
    }
    Node2 *curr=node(*linked,i);
    return curr->data;
}

void l2_des(LinkedList2 **linked){
    LinkedList2 *L=*linked;
    Node2 *node = L->head;
    for (;node != NULL; node = L->head) {
        L->head = node->next;
        node->prev = NULL;
        node->next = NULL;
        free(node);
        L->size--;
    }
    (*linked)->head = NULL;
    (*linked)->tail = NULL;
}


Node2* node(LinkedList2 *linked,int index) {
    // assert isElementIndex(index);
    if (index < (linked->size >> 1)) {
        Node2 *x = linked->head;
        for (int i = 0; i < index; i++){
            x = x->next;
        }
        return x;
    } else {
        Node2 *x = linked->tail;
        for (int i = linked->size - 1; i > index; i--){
            x = x->prev;
        }
        return x;
    }
}

static bool checkPositionIndex(int size,int index){
    return index >= 0 && index <= size;
}

void linkBefore(LinkedList2 **linked,L2_DataType e, Node2 *succ) {
    // assert succ != null;
    Node2 *pred = succ->prev;
    Node2 *newNode = createNode(e, pred, succ);
    succ->prev = newNode;
    if (pred == NULL){
        (*linked)->head = newNode;
    } else {
        pred->next = newNode;
    }
    (*linked)->size++;
}

void linkFirst(LinkedList2 **linked,L2_DataType e) {
    LinkedList2 *L = *linked;
    Node2 *h = L->head;
    Node2 *newNode = createNode(e, NULL, h);
    L->head = newNode;
    if (h == NULL){
        L->tail = newNode;
    } else {
        h->prev = newNode;
    }

    L->size++;
}

void linkLast(LinkedList2 **linked,L2_DataType e) {
    LinkedList2 *link = *linked;
    Node2* l = link->tail;
    Node2 *newNode = createNode(e, l, NULL);
    link->tail = newNode;
    if (l == NULL) {
        link->head = newNode;
    } else {
        l->next = newNode;
    }
    link->size++;
}
bool checkElementIndex(LinkedList2 *linked,int index) {
    return index >= 0 && index < linked->size;
}
int unlink(LinkedList2 **linked,Node2* x) {
    // assert x != null;
    L2_DataType element = x->data;
    Node2 *next = x->next;
    Node2 *prev = x->prev;

    if (prev == NULL) {
        (*linked)->head = next;
    } else {
        prev->next = next;
        x->prev = NULL;
    }

    if (next == NULL) {
        (*linked)->tail = prev;
    } else {
        next->prev = prev;
        x->next = NULL;
    }

    x->data = 0;
    (*linked)->size--;
    return element;
}

int unlinkFirst(LinkedList2 **linked,Node2 *f) {
    // assert f == first && f != null;
    LinkedList2 *L = *linked;
    L2_DataType element = f->data;
    Node2 *next = f->next;
    f->data = 0;
    f->next = NULL;
    L->head = next;
    if (next == NULL){
        L->tail = NULL;
    } else {
        next->prev = NULL;
    }
    L->size--;
    return element;
}

int unlinkLast(LinkedList2 **linked,Node2 *f) {
    // assert f == first && f != null;
    LinkedList2 *L = *linked;
    L2_DataType element = f->data;
    Node2 *prev = f->prev;
    f->data = 0;
    f->prev = NULL;
    L->tail = prev;
    if (prev == NULL){
        L->head = NULL;
    } else {
        prev->next = NULL;
    }
    L->size--;
    return element;
}

#endif //STUDY_C_202203_LINKEDLIST2_C

// main.c

#include "linear_struct/linked/LinkedList2.h"
void test_one_linked2(){
    LinkedList2 *linkedList2;
    int i;
    l2_LinkedListInit(&linkedList2);
    for (i = 0; i < 10; i++) {
        l2_insert_index(&linkedList2,i,i+1);
    }
    int del_first = l2_del(&linkedList2);
    printf("%d \n",del_first);
    int del_index = l2_del_index(&linkedList2,2);
    printf("%d \n",del_index);
    int del_last = l2_del_last(&linkedList2);
    printf("%d \n",del_last);
    for (i = 0; i < l2_length(linkedList2); i++) {
        int del = l2_get_index(&linkedList2, i);
        printf("%d \n",del);
    }
    l2_des(&linkedList2);
    free(linkedList2);
    linkedList2 = NULL;
}
int main() {
    test_one_linked2();
    return 0;
}

1.1.5 队列

1. 队列的定义
       队列也是一种特殊的线性表，队列的数据元素及数据元素间的逻辑关系和线性表的完全相同，其差别是：线性表允许在任意位置插入和删除数据元素，而队列只允许在其一端进行插入操作，在其另一端进行删除操作。队列是先进先出原则。
2. 队列的操作与实现
        队列可以由线性表实现（即数组），也可以用链表实现，我们基于链表写一个队列的实现，（备注：基于简单数组实现对头出队，时涉及移动数据元素，要考虑性能。所以链表更适合些）

4. 栈

栈是线性数据结构，有先进后出，或者后进先出的特点。程序只能操作栈顶元素，而栈底元素是不允许操作。就像一个桶，取东西时只能从上往下取一样。
栈常应用于实现递归功能方面的场景，例如斐波那契数列。

5. 树

• 树的定义

树是由n(n>=1)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点： 每个节点有零个或多个子节点；没有父节点的节点称为根节点；每一个非根节点有且只有一个父节点；除了根节点外，每个子节点可以分为多个不相交的子树。

• 树中常用术语

度：结点的孩子结点个数即为该结点的【度】.【度】为0的结点叫叶子结点，一棵树中，最大的节点的度称为树的度；
总节点数：假设 k 为总度数，k+1=总节点数，为什么总节点数肯定比总度数多1呢？其实很简单可以解释，度可以看作节点与节点之间的线。
根：处在树的最顶端(没有双亲)的结点叫【根】结点。
节点的层次：从根开始定义起，根为第1层，根的子节点为第2层，以此类推。
树的高度或深度：树中节点的最大层次。

• 二叉树

二叉树（Binary tree）是树形结构的一个重要类型。许多实际问题抽象出来的数据结构往往是二叉树形式，即使是一般的树也能简单地转换为二叉树，而且二叉树的存储结构及其算法都较为简单，因此二叉树显得特别重要。二叉树特点是每个结点最多只能有两棵子树，且有左右之分

二叉树是n个有限元素的集合，该集合或者为空、或者由一个称为根（root）的元素及两个不相交的、被分别称为左子树和右子树的二叉树组成，是有序树。当集合为空时，称该二叉树为空二叉树。在二叉树中，一个元素也称作一个结点

• 二叉树的一些计算公式

设二叉树总结点数为N,度为0的叶子结点个数为n0,度为1的结点个数为n1.度为2的节点个数为n2
下面可得两等式:
(1)N = n0 + n1 + n2 ;
依据：很显然,二叉树总结点数等于度分别为0,1,2的结点个数总和。
(2) N -1 = 2n2 + n1 即 N = 2n2 + n1 + 1 ；
依据：二叉树的树杆(即左右斜线)数等于总结点数减1,这个隐含的条件很关键哦！！！
由(1)(2)两式即可求得: n0=n2+1 ；

（1） 非空二叉树叶子结点数 = 度为2的结点数 + 1 即，0 = 2 + 1
（2） 非空二叉树上第K层至多有2−1 个结点（≥1）
（3） 高度为H的二叉树至多有2−1 个结点（≥1）
（4） 具有N个（>0）结点的完全二叉树的高度为 ⌈₂(+1)⌉ 或 ⌊₂⌋+1
（5） 对完全二叉树按从上到下、从左到右的顺序依次编号1,2，…，N，则有以下关系：

a) 当 >1 时，结点  的双亲结点编号为 ⌊/2⌋ ，即当  为偶数时，其双亲结点的编号为/2 ，它是
双亲结点的左孩子；当  为奇数时，其双亲结点的编号为 (−1)/2 ，它是双亲结点的右孩子。
b) 当 2≤ 时，结点i的左孩子编号为 2 ，否则无左孩子。
c) 当 2+1≤ 时，结点i的右孩子编号为 2+1 ，否则无右孩子。
d) 结点  所在层次（深度）为 ⌊~2~⌋+1 。（设根结点为第1层）

• 满二叉树

一个二叉树，如果每一个层的结点数都达到最大值，则这个二叉树就是满二叉树。也就是说，如果一个二叉树的层数为K，且结点总数是(2^k) -1 ，则它就是满二叉树

• 完全二叉树

一棵深度为k的有n个结点的二叉树，对树中的结点按从上至下、从左到右的顺序进行编号，如果编号为i（1≤i≤n）的结点与满二叉树中编号为i的结点在二叉树中的位置相同，则这棵二叉树称为完全二叉 树
完全二叉树的特点： 叶子结点只能出现在最下层和次下层，且最下层的叶子结点集中在树的左部。需要注意的是，满二叉树肯定是完全二叉树，而完全二叉树不一定是满二叉树。

6. 散列

7. 堆

8. 图

java数据结构

1. 8大基本数据类型

1.1 整形

byte short int long

1.2 浮点型

float double

1.3 字符型

char

1.4 布尔型

boolean

数据类型名称	占用字节	取值范围	默认值	包装类
byte(字节)	1(8位)	-128～127	0	Byte
short(短整型)	2(16位)	-32768～32767	0	Short
int (整型)	4(32位)	-2147483648～2147483647	0	Integer
long(长整型)	8(64位)	-9223372036854774808～9223372036854774807	0L	Long
char(字符型)	2(16位)	‘a’,10,8,16进制,中文字符	\u0000	Float
float(单精度浮点型)	4(32位)	3.402823e+38～1.401298e-45	0.0F	Float
double(双精度浮点型)	8(64位)	1.797693e+308～4.9000000e-324	0.00	Double
boolean(双精度浮点型)	如果为boolean则占用4位,如果为boolean[] 则占用1位	true | false	false	Double