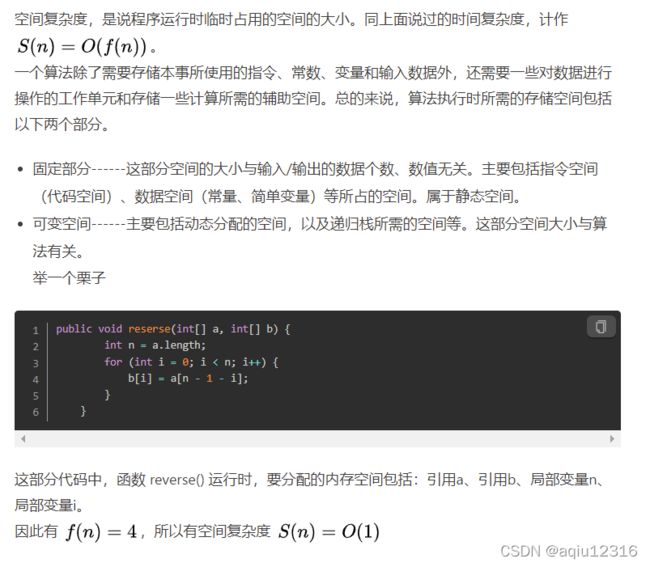
详解校招算法与数据结构
算法与数据结构(java)版
一,数据结构
1,数组和链表
(1)数组
数组是最常见的一种数据结构,它是相同类型的用一个标识符封装到一起的基本类型数据序列或者对象序列。数组使用一个统一的数组名和不同的下标来唯一确定数组中的元素。实质上,数组是一个简单的线性序列,因此访问速度很快。
数组的创建
type[] arrayName; // 数据类型[] 数组名; 或 type arrayName[]; // 数据类型 数组名[];
空间分配
声明了数组,只是得到了一个存放数组的变量,并没有为数组元素分配内存空间,不能使用。因此要为数组分配内存空间,这样数组的每一个元素才有一个空间进行存储。
arrayName = new type[size]; // 数组名 = new 数据类型[数组长度];
在图 1 中 arr 为数组名称,方括号“[]”中的值为数组的下标。数组通过下标来区分数组中不同的元素,并且下标是从 0 开始的。因此这里包含6 个元素的 arr 数组最大下标为 5。
注意:一旦声明了数组的大小,就不能再修改。这里的数组长度也是必需的,不能少。
存取值
获取单个元素是指获取数组中的一个元素,如第一个元素或最后一个元素。
arrayName[index]; //取值 arrayName[index] = value; //存值
其中,arrayName 表示数组变量,index 表示下标,下标为 0 表示获取第一个元素,下标为 array.length-1 表示获取最后一个元素。
当指定的下标值超出数组的总长度时,会拋出 ArraylndexOutOfBoundsException 异常。
数组的长度和遍历
当数组中的元素数量不多时,要获取数组中的全部元素,可以使用下标逐个获取元素。但是,如果数组中的元素过多,再使用单个下标则显得烦琐,此时使用一种简单的方法可以获取全部元素——使用循环语句。
int[] number = {1,2,3,5,8};
for (int i=0;i
多维数组
多维数组可以看成是数组的数组,比如二维数组就是一个特殊的一维数组,其每一个元素都是一个一维数组
type[][] typeName = new type[typeLength1][typeLength2];
排序
杨辉三角
多和图片相关
(2)链表
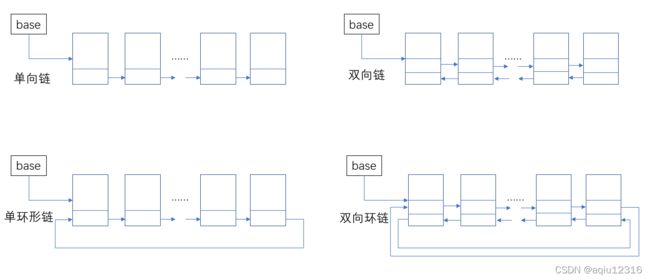
链表是一种物理存储单元上非连续、非顺序的存储结构,数据元素的逻辑顺序是通过链表中的指针连接次序实现的。
每一个链表都包含多个节点,节点又包含两个部分,一个是数据域(储存节点含有的信息),一个是引用域(储存下一个节点或者上一个节点的地址)。
链表的特点
获取数据麻烦,需要遍历查找,比数组慢;方便插入、删除。
链表的实现
-
创建一个节点类,其中节点类包含两个部分,第一个是数据域(你到时候要往节点里面储存的信息),第二个是引用域(相当于指针,单向链表有一个指针,指向下一个节点;双向链表有两个指针,分别指向下一个和上一个节点)
-
创建一个链表类,其中链表类包含三个属性:头结点、尾节点和大小,方法包含添加、删除、插入等等方法。
//单链表节点类
public class Node {
public Object data;
public Node next;
public Node(Object e){
this.data = e;
}
}
//双向链表节点类
public class Node {
public Object e;
public Node next;
public Node pre;
public Node(){
}
public Node(Object e){
this.e = e;
next = null;
pre = null;
}
}
package MutuLink;
public class MyList {
private Node head;
private Node tail;
private int size = 0;
public MyList() {
head = new Node();
tail = new Node();
head.next =null;
tail.pre = null;
}
public boolean empty() {
if (head.next == null)
return true;
return false;
}
//找到所找下标节点的前一个节点
public Node findpre(int index){
Node rnode = head;
int dex = -1;
while(rnode.next != null){
//找到了插入节点的上一个节点
if( dex== index - 1){
return rnode;
}
rnode = rnode.next;
dex++;
}
return null;
}
public Node findthis(int index){
Node rnode = head;
//把rnode想象为指针,dex为指向的下标,这个地方很容易错,因为当指向最后一个节点时没有判断IF就跳出循环了
int dex = -1;
while(rnode.next != null){
if(dex == index)
return rnode;
rnode = rnode.next;
dex++;
}
if(dex == size - 1){
return rnode;
}
// Node test = new Node(new Students("haha",1,2));
return null;
}
// 往链表末尾加入节点
public void add(Object e) {
Node node = new Node(e);
Node rnode = head;
//如果是空链表的话插入一个节点,这个节点的pre不能指向上一个节点,必须指空
if (this.empty()) {
rnode.next = node;
rnode.next.pre = null;
tail.pre = node;
size++;
} else {
while (rnode.next != null)
rnode = rnode.next;
rnode.next = node;
node.pre = rnode;
tail.pre = node;
size++;
}
}
//往链表的某一个标插入一个节点
public boolean add(int index,Object e){
if(index <0||index>=size)
return false;
Node node = new Node(e);
Node prenode = this.findpre(index);
node.next = prenode.next;
prenode.next.pre = node;
prenode.next = node;
node.pre = prenode;
size++;
return true;
}
public boolean add(int index,MyList myl){
if(index <0 || index >= size)
return false;
Node prenode = this.findpre(index);
// myl.tail.pre.next = prenode.next;
// prenode.pre = myl.tail.pre;
// tail.pre = null;
// prenode.next = myl.head.next;
// myl.head.next.pre = prenode;
// head.next = null;
myl.tail.pre.next = prenode.next;
prenode.next.pre = myl.tail.pre.pre;
myl.head.next.pre = prenode.pre;
prenode.next = myl.head.next;
myl.head = null;
myl.tail = null;
size+=myl.size;
return true;
}
public Object remove(int index){
Object ob= this.get(index);
if(index <0 || index >= size)
return null;
//特殊情况,当移除节点是最后一个节点的时候
//较为复杂通过画图来写代码
if(index == size - 1){
Node prenode = this.findpre(index);
this.tail.pre = this.tail.pre.pre;
this.tail.pre.next.pre = null;
this.tail.pre.next =null;
size--;
return ob;
}
//比较复杂,通过画图解决
else{
Node prenode = this.findpre(index);
prenode.next = prenode.next.next;
prenode.next.pre.next = null;
prenode.next.pre = prenode.next.pre.pre;
size--;
return ob;
}
}
public Object get(int index){
Node thisnode = this.findthis(index);
return thisnode.e;
}
public int size(){
return size;
}
}
2,栈和队列
(1)栈
栈(英语:stack)又称为堆栈或堆叠,栈作为一种数据结构,是一种只能在一端进行插入和删除操作的特殊线性表。它按照先进后出的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶,需要读数据的时候从栈顶开始弹出数据(最后一个数据被第一个读出来)。栈具有记忆作用,对栈的插入与删除操作中,不需要改变栈底指针。
栈是允许在同一端进行插入和删除操作的特殊线性表。允许进行插入和删除操作的一端称为栈顶(top),另一端为栈底(bottom);栈底固定,而栈顶浮动;栈中元素个数为零时称为空栈。插入一般称为进栈(PUSH),删除则称为退栈(POP)。
由于堆叠数据结构只允许在一端进行操作,因而按照后进先出(LIFO, Last In First Out)的原理运作。栈也称为后进先出表。
这里以羽毛球筒为例,羽毛球筒就是一个栈,刚开始羽毛球筒是空的,也就是空栈,然后我们一个一个放入羽毛球,也就是一个一个push进栈,当我们需要使用羽毛球的时候,从筒里面拿,也就是pop出栈,但是第一个拿到的羽毛球是我们最后放进去的。
package com.aqiu.datastructure;
import java.util.Arrays;
import java.util.EmptyStackException;
public class ArrayStack {
//存储元素的数组,声明为Object类型能存储任意类型的数据
private Object[] elementData;
//指向栈顶的指针
private int top;
//栈的总容量
private int size;
//默认构造一个容量为10的栈
public ArrayStack(){
this.elementData = new Object[10];
this.top = -1;
this.size = 10;
}
public ArrayStack(int initialCapacity){
if(initialCapacity < 0){
throw new IllegalArgumentException("栈初始容量不能小于0: "+initialCapacity);
}
this.elementData = new Object[initialCapacity];
this.top = -1;
this.size = initialCapacity;
}
//压入元素
public Object push(Object item){
//是否需要扩容
isGrow(top+1);
elementData[++top] = item;
return item;
}
//弹出栈顶元素
public Object pop(){
Object obj = peek();
remove(top);
return obj;
}
//获取栈顶元素
public Object peek(){
if(top == -1){
throw new EmptyStackException();
}
return elementData[top];
}
//判断栈是否为空
public boolean isEmpty(){
return (top == -1);
}
//删除栈顶元素
public void remove(int top){
//栈顶元素置为null
elementData[top] = null;
this.top--;
}
/**
* 是否需要扩容,如果需要,则扩大一倍并返回true,不需要则返回false
* @param minCapacity
* @return
*/
public boolean isGrow(int minCapacity){
int oldCapacity = size;
//如果当前元素压入栈之后总容量大于前面定义的容量,则需要扩容
if(minCapacity >= oldCapacity){
//定义扩大之后栈的总容量
int newCapacity = 0;
//栈容量扩大两倍(左移一位)看是否超过int类型所表示的最大范围
if((oldCapacity<<1) - Integer.MAX_VALUE >0){
newCapacity = Integer.MAX_VALUE;
}else{
newCapacity = (oldCapacity<<1);//左移一位,相当于*2
}
this.size = newCapacity;
int[] newArray = new int[size];
elementData = Arrays.copyOf(elementData, size);
return true;
}else{
return false;
}
}
}
利用栈判断分隔符是否匹配
写过xml标签或者html标签的,我们都知道<必须和最近的>进行匹配,[ 也必须和最近的 ] 进行匹配。
比如:这是符号相匹配的,如果是 abc] 那就是不匹配的。
对于 12,我们分析在栈中的数据:遇到匹配正确的就消除
最后栈中的内容为空则匹配成功,否则匹配失败!!!
//分隔符匹配
//遇到左边分隔符了就push进栈,遇到右边分隔符了就pop出栈,看出栈的分隔符是否和这个有分隔符匹配
@Test
public void testMatch(){
ArrayStack stack = new ArrayStack(3);
String str = "12";
char[] cha = str.toCharArray();
for(char c : cha){
switch (c) {
case '{':
case '[':
case '<':
stack.push(c);
break;
case '}':
case ']':
case '>':
if(!stack.isEmpty()){
char ch = stack.pop().toString().toCharArray()[0];
if(c=='}' && ch != '{'
|| c==']' && ch != '['
|| c==')' && ch != '('){
System.out.println("Error:"+ch+"-"+c);
}
}
break;
default:
break;
}
}
}
(2)队列
队列(queue)是一种特殊的线性表,特殊之处在于它只允许在表的前端(front)进行删除操作,而在表的后端(rear)进行插入操作,和栈一样,队列是一种操作受限制的线性表。进行插入操作的端称为队尾,进行删除操作的端称为队头。队列中没有元素时,称为空队列。
队列的数据元素又称为队列元素。在队列中插入一个队列元素称为入队,从队列中删除一个队列元素称为出队。因为队列只允许在一端插入,在另一端删除,所以只有最早进入队列的元素才能最先从队列中删除,故队列又称为先进先出(FIFO—first in first out)线性表。
比如我们去电影院排队买票,第一个进入排队序列的都是第一个买到票离开队列的人,而最后进入排队序列排队的都是最后买到票的。
在比如在计算机操作系统中,有各种队列在安静的工作着,比如打印机在打印列队中等待打印。
队列分为:
①、单向队列(Queue):只能在一端插入数据,另一端删除数据。
②、双向队列(Deque):每一端都可以进行插入数据和删除数据操作。
这里我们还会介绍一种队列——优先级队列,优先级队列是比栈和队列更专用的数据结构,在优先级队列中,数据项按照关键字进行排序,关键字最小(或者最大)的数据项往往在队列的最前面,而数据项在插入的时候都会插入到合适的位置以确保队列的有序。
单向队列
在实现之前,我们先看下面几个问题:
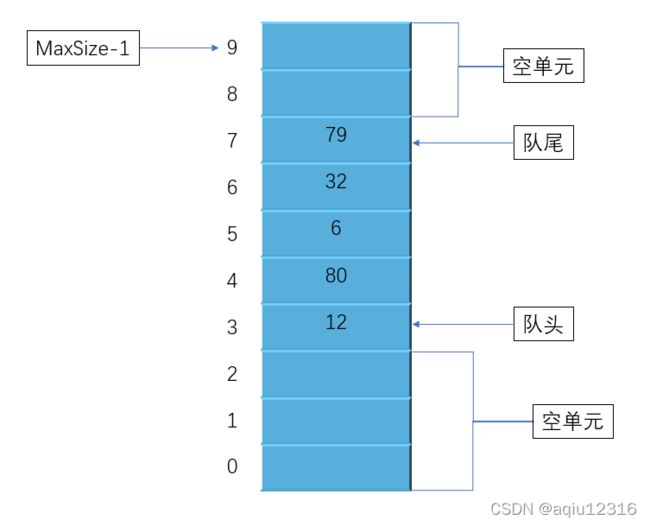
①、与栈不同的是,队列中的数据不总是从数组的0下标开始的,移除一些队头front的数据后,队头指针会指向一个较高的下标位置,如下图:
②、我们再设计时,队列中新增一个数据时,队尾的指针rear 会向上移动,也就是向下标大的方向。移除数据项时,队头指针 front 向上移动。那么这样设计好像和现实情况相反,比如排队买电影票,队头的买完票就离开了,然后队伍整体向前移动。在计算机中也可以在队列中删除一个数之后,队列整体向前移动,但是这样做效率很差。我们选择的做法是移动队头和队尾的指针。
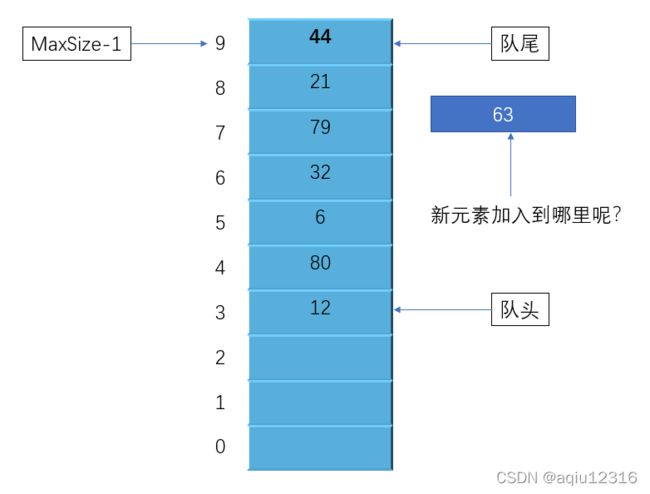
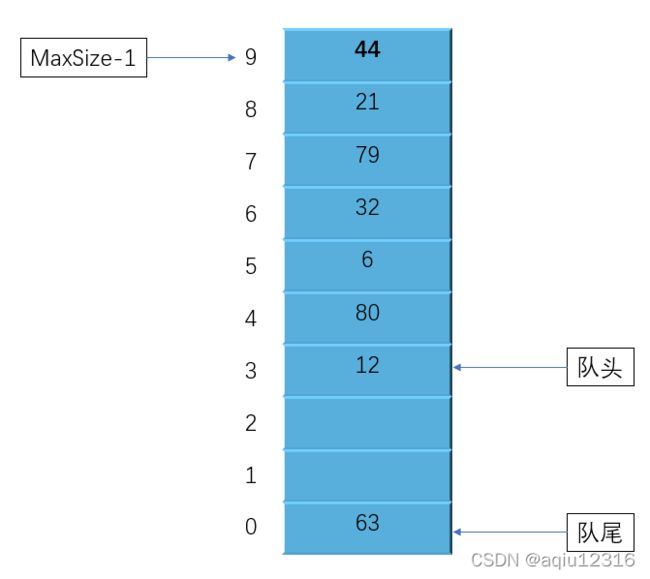
③、如果向第②步这样移动指针,相信队尾指针很快就移动到数据的最末端了,这时候可能移除过数据,那么队头会有空着的位置,然后新来了一个数据项,由于队尾不能再向上移动了,那该怎么办呢?如下图:
为了避免队列不满却不能插入新的数据,我们可以让队尾指针绕回到数组开始的位置,这也称为“循环队列”。
package com.aqiu.datastructure;
public class MyQueue {
private Object[] queArray;
//队列总大小
private int maxSize;
//前端
private int front;
//后端
private int rear;
//队列中元素的实际数目
private int nItems;
public MyQueue(int s){
maxSize = s;
queArray = new Object[maxSize];
front = 0;
rear = -1;
nItems = 0;
}
//队列中新增数据
public void insert(int value){
if(isFull()){
System.out.println("队列已满!!!");
}else{
//如果队列尾部指向顶了,那么循环回来,执行队列的第一个元素
if(rear == maxSize -1){
rear = -1;
}
//队尾指针加1,然后在队尾指针处插入新的数据
queArray[++rear] = value;
nItems++;
}
}
//移除数据
public Object remove(){
Object removeValue = null ;
if(!isEmpty()){
removeValue = queArray[front];
queArray[front] = null;
front++;
if(front == maxSize){
front = 0;
}
nItems--;
return removeValue;
}
return removeValue;
}
//查看对头数据
public Object peekFront(){
return queArray[front];
}
//判断队列是否满了
public boolean isFull(){
return (nItems == maxSize);
}
//判断队列是否为空
public boolean isEmpty(){
return (nItems ==0);
}
//返回队列的大小
public int getSize(){
return nItems;
}
}
双端队列
双端队列就是一个两端都是结尾或者开头的队列, 队列的每一端都可以进行插入数据项和移除数据项,这些方法可以叫做:
insertRight()、insertLeft()、removeLeft()、removeRight()
如果严格禁止调用insertLeft()和removeLeft()(或禁用右端操作),那么双端队列的功能就和前面讲的栈功能一样。
如果严格禁止调用insertLeft()和removeRight(或相反的另一对方法),那么双端队列的功能就和单向队列一样了。
优先级队列
优先级队列(priority queue)是比栈和队列更专用的数据结构,在优先级队列中,数据项按照关键字进行排序,关键字最小(或者最大)的数据项往往在队列的最前面,而数据项在插入的时候都会插入到合适的位置以确保队列的有序。
优先级队列 是0个或多个元素的集合,每个元素都有一个优先权,对优先级队列执行的操作有:
(1)查找
(2)插入一个新元素
(3)删除
一般情况下,查找操作用来搜索优先权最大的元素,删除操作用来删除该元素 。对于优先权相同的元素,可按先进先出次序处理或按任意优先权进行。
这里我们用数组实现优先级队列,这种方法插入比较慢,但是它比较简单,适用于数据量比较小并且不是特别注重插入速度的情况。
后面我们会讲解堆,用堆的数据结构来实现优先级队列,可以相当快的插入数据。
数组实现优先级队列,声明为int类型的数组,关键字是数组里面的元素,在插入的时候按照从大到小的顺序排列,也就是越小的元素优先级越高。
package com.aqiu.datastructure;
public class PriorityQue {
private int maxSize;
private int[] priQueArray;
private int nItems;
public PriorityQue(int s){
maxSize = s;
priQueArray = new int[maxSize];
nItems = 0;
}
//插入数据
public void insert(int value){
int j;
if(nItems == 0){
priQueArray[nItems++] = value;
}else{
j = nItems -1;
//选择的排序方法是插入排序,按照从大到小的顺序排列,越小的越在队列的顶端
while(j >=0 && value > priQueArray[j]){
priQueArray[j+1] = priQueArray[j];
j--;
}
priQueArray[j+1] = value;
nItems++;
}
}
//移除数据,由于是按照大小排序的,所以移除数据我们指针向下移动
//被移除的地方由于是int类型的,不能设置为null,这里的做法是设置为 -1
public int remove(){
int k = nItems -1;
int value = priQueArray[k];
priQueArray[k] = -1;//-1表示这个位置的数据被移除了
nItems--;
return value;
}
//查看优先级最高的元素
public int peekMin(){
return priQueArray[nItems-1];
}
//判断是否为空
public boolean isEmpty(){
return (nItems == 0);
}
//判断是否满了
public boolean isFull(){
return (nItems == maxSize);
}
}
insert() 方法,先检查队列中是否有数据项,如果没有,则直接插入到下标为0的单元里,否则,从数组顶部开始比较,找到比插入值小的位置进行插入,并把 nItems 加1.
remove 方法直接获取顶部元素。
优先级队列的插入操作需要 O(N)的时间,而删除操作则需要O(1) 的时间,后面会讲解如何通过 堆 来改进插入时间。
3,树
(1)树,二叉树
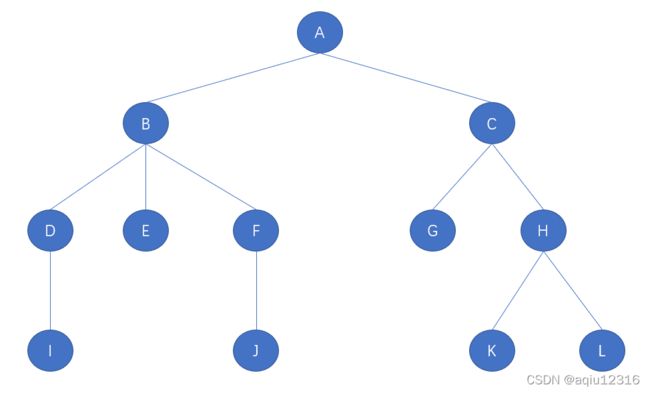
树是一种非线性的数据结构,是由n(n>=1)个有限节点组成的有层次关系的集合,在树中有许多节点,每一个节点最多只有一个父节点,并且可能会有0个或者更多个子节点,没有父节点的那个称为根节点,除了根节点外,每个节点又可分为多个不相交的子树。
树的相关概念术语:
1)节点
2)根节点或树根
3)子树
4)节点的度:一个节点直接含有的子树的个数,称之为节点的度。比如上图中B节点的度为3,C节点的度是2,I、J、K、L节点的度是0
5)叶子节点、叶节点、终端节点:度为0的节点叫做叶子节点,也叫叶节点、终端节点,其实就是没有子节点的节点,或者说没有子树的节点
6)双亲节点、父节点:父节点就是一个节点上头的那个节点,如果一个节点包含若干子节点,那么这个节点就是这些子节点的父节点,也叫双亲节点
7)兄弟节点:拥有相同父节点的节点互称为兄弟节点
8)树的度:一棵树中最大节点的度称之为树的度,即树中哪个节点的子节点最多,那么这个节点的度也就是树的度
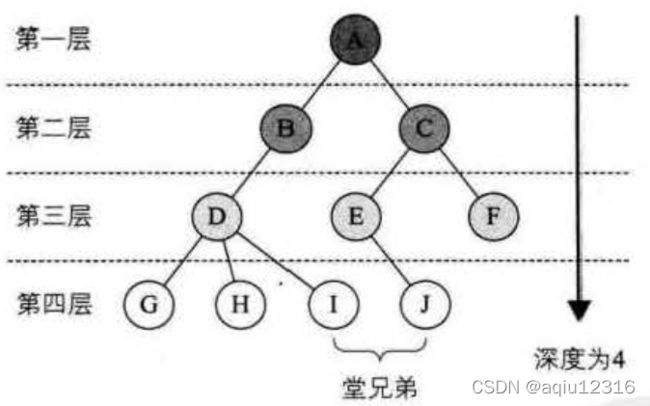
9)节点的层次:从根这一层开始,根算1层,根的子节点算2层,一直到最下面一层
10)树的高度、深度(这里属于树的层次结构):
树的深度是从根节点开始、自顶向下逐层累加(根节点的高度是1)助记:深度从上到下 树的高度是从叶节点开始、自底向上逐层累加(叶节点的高度是1)助记:高度由下向上 虽然树的高度和深度一样,但是具体到某个节点上,其高度和深度通常是不一样的。
11)堂兄弟节点:堂兄弟节点是同一层,父节点不同,或者说双亲节点在同一层的节点称之为堂兄弟节点
12)节点的祖先:从根节点到某一节点一路顺下来的除了该节点的所有节点都是该节点的祖先节点
13)节点的子孙:以某节点为根的子树中,任何一个节点都是其子孙,也就是说这个节点下面与这个节点有关的节点都是这个节点的子孙
14)森林:由m棵不相交的树组成的集合,叫做森林,对比树中每个节点的子树的集合其实就构成了森林。
二叉树
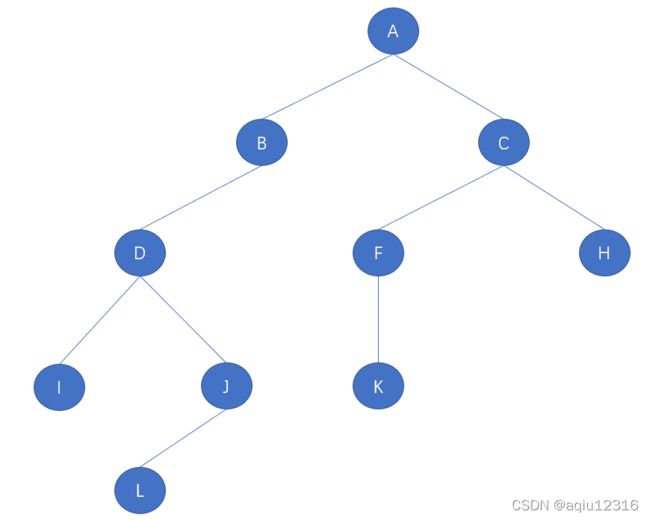
对于在某个阶段都是两种结果的情形,比如开和关、0和1、真和假、上和下、对与错、正面与反面,都适合用树状结构来建模,这种树是一种很特殊的树状结构,称之为二叉树。对于上图中的树由于D有三个节点,所以它不是二叉树。
二叉树中不存在子树或者有一棵子树都是可以的。左子树和右子树是有顺序的,次序不能任意颠倒。即使树中某节点只有一棵子树也要区分它是左子树还是右子树。
斜树:线性表就是一种树的极其特殊的表现形式。比如上面的树2和树5。
满二叉树:非叶子节点的度一定是2。
完全二叉树:满二叉树一定是完全二叉树,但是完全二叉树不一定是满二叉树。(按层次编号一一对应)相当于是满二叉树的某些位置去掉之后的树,形式上还是满足满二叉树的形式的。
(1)叶子节点只能出现在最下两层
(2)最下层叶子一定集中在左部连续位置
(3)倒数二层,若有叶子节点,一定都在右部连续位置
(4)如果节点度为1,则该结点只有左孩子,即不存在只有右子树的情况
(5)同样结点数的二叉树,完全二叉树的深度最小
二叉树的性质:
性质1:在二叉树的第i层上至多有2^(i-1)个节点(i>=1)。
性质2:深度为k的二叉树至多有2^k-1个节点(k>=1)。最多就是满二叉树的情况。
性质3:对任何一棵二叉树T,如果其终端节点数(叶子节点数)为n0,度为2的节点数为n2,则n0=n2+1。(除了叶子节点外只有度为1或2的节点数了)
性质4:具有n个节点的完全二叉树的深度为【log2n】+1(【x】表示不大于x的最大整数)。由于深度为k的满二叉树的节点数n一定是2^k-1,这个深度就是该二叉树的度,所以反推可以得到满二叉树的度k=log2(n+1)。
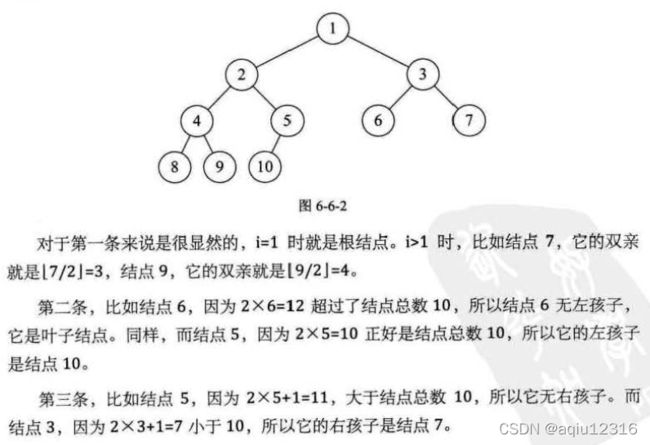
性质5:如果对一棵有n个节点的完全二叉树(其深度为【log2n】+1)的节点按层序编号(从第一层到第【log2n】+1层,每层从左到右),对任一节点i(1<=i<=n)有:
(2)搜索树(查找树)
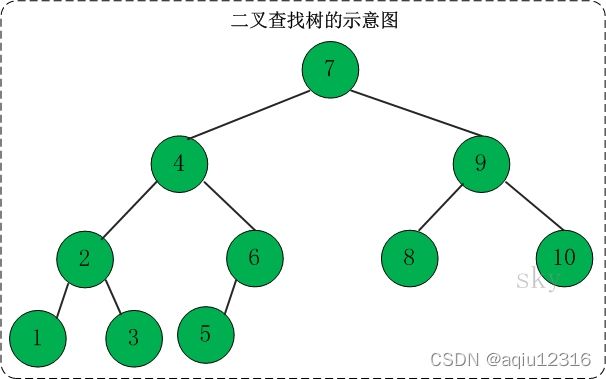
二叉查找树(Binary Search Tree),又被称为二叉搜索树。 它是特殊的二叉树:对于二叉树,假设x为二叉树中的任意一个结点,x节点包含关键字key,节点x的key值记为key[x]。如果y是x的左子树中的一个结点,则key[y] <= key[x];如果y是x的右子树的一个结点,则key[y] >= key[x]。那么,这棵树就是二叉查找树。如下图所示:
在二叉查找树中: (01) 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值; (02) 任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值; (03) 任意节点的左、右子树也分别为二叉查找树。 (04) 没有键值相等的节点(no duplicate nodes)。
操作
-
插入
插入节点的过程是:若原二叉查找树为空,则直接插入;否则,若关键字 k 小于根节点关键字,则插入到左子树中,若关键字 k 大于根节点关键字,则插入到右子树中。注意每次插入的节点必是叶节点。
-
删除
二叉查找树的删除操作是相对复杂一点,它要按 3 种情况来处理:
若被删除节点 t 是叶子节点,则直接删除,不会破坏二叉排序树的性质;
若节点 t 只有左子树或只有右子树,则让 t 的子树成为 t 父节点的子树,替代 t 的位置;
若节点 t 既有左子树,又有右子树,则用 t 的直接前驱或者直接后继代替 t,然后从二叉查找树中删除这个后继,这样就转换成了第一或第二种情况。
-
查找
查找是从根节点开始,若二叉树非空,将给定值与根节点的关键字比较,若相等,则查找成功;若不等,则当给定值小于根节点关键字时,在根节点的左子树中查找,否则在根节点的右子树中查找。
其查找平均时间复杂度为O(logn),但是最差情况为插入的节点是有序的,则该二叉搜索树会变成左斜树(或者右斜树或者可以理解为“链表”),即最差时间复杂度为O(n),故而查找性能不是严格意义上的O(logn),不稳定。
搜索树实现:
public class SortedBinaryTree {undefined
private Node root; // 根节点
private int size; // 二叉树元素个数
/**
* 二叉树节点
*/
private static class Node {undefined
E element; // 节点元素
Node lChild; // 左孩子
Node rChild; // 右孩子
public Node(E element) {undefined
this(element, null, null);
}
public Node(E element, Node lChild, Node rChild) {undefined
this.element = element;
this.lChild = lChild;
this.rChild = rChild;
}
}
public SortedBinaryTree(List elements) {undefined
for (E e : elements) {undefined
add(e);
}
}
public SortedBinaryTree(E[] elements) {undefined
for (E e : elements) {undefined
add(e);
}
}
public SortedBinaryTree() {undefined
}
/**
* 判断当前元素是否存在于树中
*
* @param element
* @return
*/
public boolean contains(E element) {undefined
return search(root, element);
}
/**
* 递归搜索,查找当前以curRoot为根节点的树中element存在与否
*
* @param curRoot
* @param element
* @return
*/
@SuppressWarnings("unchecked")
private boolean search(Node curRoot, E element) {undefined
if (curRoot == null)
return false;
Comparable super E> e = (Comparable super E>) element;
int cmp = e.compareTo(curRoot.element);
if (cmp > 0) {undefined
// 查找的元素大于当前根节点对应的元素,向右走
return search(curRoot.rChild, element);
} else if (cmp < 0) {undefined
// 查找的元素小于当前根节点对应的元素,向左走
return search(curRoot.lChild, element);
} else {undefined
// 查找的元素等于当前根节点对应的元素,返回true
return true;
}
}
/**
* 非递归搜索,查找当前以curRoot为根节点的树中的element是否存在
*
* @param curRoot
* 二叉排序树的根节点
* @param element
* 被搜索的元素
* @param target
* target[0]指向查找路径上最后一个节点: 如果当前查找的元素存在,则target[0]指向该节点
* @return
*/
@SuppressWarnings("unchecked")
private boolean find(Node curRoot, E element, Node[] target) {undefined
if (curRoot == null)
return false;
Node tmp = curRoot;
Comparable super E> e = (Comparable super E>) element;
while (tmp != null) {undefined
int cmp = e.compareTo(tmp.element);
target[0] = tmp;
if (cmp > 0) {undefined
// 查找的元素大于当前节点对应的元素,向右走
tmp = tmp.rChild;
} else if (cmp < 0) {undefined
// 查找的元素小于当前节点对应的元素,向左走
tmp = tmp.lChild;
} else {undefined
// 查找的元素等于当前根节点对应的元素,返回true
return true;
}
}
return false;
}
/**
* 向二叉排序树中添加元素,如果当前元素已经存在,则添加失败,返回false,如果当前元素不存在,则添加成功,返回true
*
*/
@SuppressWarnings("unchecked")
public boolean add(E element) {undefined
if (root == null) {undefined
root = new Node(element);
size++;
return true;
}
Node[] target = new Node[1];
if (!find(root, element, target)) {undefined
// 当前元素不存在,插入元素
// 此时target节点即为需要插入的节点的父节点
Comparable super E> e = (Comparable super E>) element;
int cmp = e.compareTo(target[0].element);
Node newNode = new Node(element);
if (cmp > 0) {undefined
// 插入的元素大于target指向的节点元素
target[0].rChild = newNode;
} else {undefined
// 插入的元素小于target指向的节点元素
target[0].lChild = newNode;
}
size++;
return true;
}
return false;
}
/**
* 删除二叉排序树中的元素,如果当前元素不存在,则删除失败,返回false;如果当前元素存在,则删除该元素,重构二叉树,返回true
*
* @param element
* @return
*/
@SuppressWarnings("unchecked")
public boolean remove(E element) {undefined
Node[] target = new Node[1];
if (find(root, element, target)) {undefined
// 被删除的元素存在,则继续执行删除操作
remove(target[0]);
return true;
}
return false;
}
/**
* 释放当前节点
*
* @param node
*/
private void free(Node node) {undefined
node.element = null;
node.lChild = null;
node.rChild = null;
node = null;
}
/**
* 删除二叉排序树中指定的节点
*
* @param node
*/
private void remove(Node node) {undefined
Node tmp;
if (node.lChild == null && node.rChild == null) {undefined
// 当前node为叶子节点,删除当前节点,则node = null;
node = null;
} else if (node.lChild == null && node.rChild != null) {undefined
// 如果被删除的节点左子树为空,则只需要重新连接其右子树
tmp = node;
node = node.rChild;
free(tmp);
} else if (node.lChild != null && node.rChild == null) {undefined
// 如果被删除的节点右子树为空,则只需要重新连接其左子树
tmp = node;
node = node.lChild;
free(tmp);
} else {undefined
// 当前被删除的节点左右子树均存在,不为空
// 找到离当前node节点对应元素且最近的节点target(左子树的最右边节点 或者 右子树最左边节点)
// 将node节点元素替换成target节点的元素,将target节点删除
tmp = node; // tmp是target的父节点
Node target = node.lChild; // 找到左子树最大子树
while (target.rChild != null) { // 在左子树中进行右拐
tmp = target;
target = target.rChild;
}
node.element = target.element; // node.element元素替换为target.element
if (tmp == node) {undefined
// tmp == node 说明没有在左子树中进行右拐,也就是node节点的左孩子没有右孩子,
// 需要重新连接tmp节点左孩子
tmp.lChild = target.lChild;
} else {undefined
// tmp != node, 进行了右拐,那么将重新连接tmp的右子树,将target.lChild赋值给tmp.rChild
tmp.rChild = target.lChild;
}
// 释放节点
free(target);
}
// 删除成功,size--;
size--;
}
public int size() {undefined
return size;
}
public boolean isEmpty() {undefined
return size() == 0;
}
public List preOrderTraverse() {undefined
List list = new ArrayList();
preOrderTraverse(root, list);
return list;
}
private void preOrderTraverse(Node curRoot, List list) {undefined
if (curRoot == null)
return;
E e = curRoot.element;
list.add(e);
preOrderTraverse(curRoot.lChild, list);
preOrderTraverse(curRoot.rChild, list);
}
public List inOrderTraverse() {undefined
List list = new ArrayList();
inOrderTraverse(root, list);
return list;
}
private void inOrderTraverse(Node curRoot, List list) {undefined
if (curRoot == null)
return;
inOrderTraverse(curRoot.lChild, list);
list.add(curRoot.element);
inOrderTraverse(curRoot.rChild, list);
}
public List postOrderTraverse() {undefined
List list = new ArrayList();
postOrderTraverse(root, list);
return list;
}
private void postOrderTraverse(Node curRoot, List list) {undefined
if (curRoot == null)
return;
inOrderTraverse(curRoot.lChild, list);
inOrderTraverse(curRoot.rChild, list);
list.add(curRoot.element);
}
/**
* 返回中序遍历结果
*/
@Override
public String toString() {undefined
return inOrderTraverse().toString();
}
public static void main(String[] args) {undefined
Integer[] elements = new Integer[] { 62, 88, 58, 47, 73, 99, 35, 51, 93, 29, 37, 49, 56, 36, 48, 50 };
SortedBinaryTree tree = new SortedBinaryTree(elements);
System.out.println(tree);
System.out.println(tree.contains(93));
System.out.println(tree.size());
System.out.println(tree.remove(47));
System.out.println(tree.preOrderTraverse());
System.out.println(tree.size());
}
}
(3)平衡树(AVL)
红黑树(Red-Black Tree,简称R-B Tree),它一种特殊的二叉查找树。 红黑树是特殊的二叉查找树,意味着它满足二叉查找树的特征:任意一个节点所包含的键值,大于等于左孩子的键值,小于等于右孩子的键值。 除了具备该特性之外,红黑树还包括许多额外的信息。
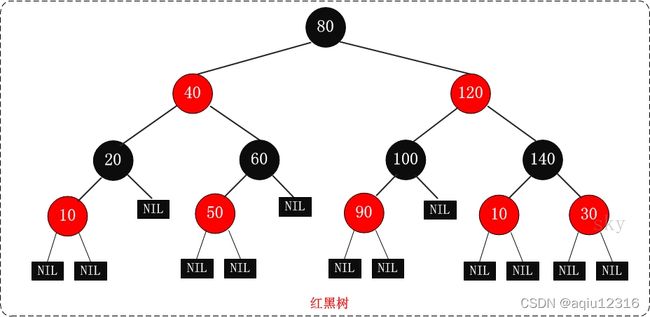
红黑树的每个节点上都有存储位表示节点的颜色,颜色是红(Red)或黑(Black)。 红黑树的特性: (1) 每个节点或者是黑色,或者是红色。 (2) 根节点是黑色。 (3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!] (4) 如果一个节点是红色的,则它的子节点必须是黑色的。 (5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
关于它的特性,需要注意的是: 第一,特性(3)中的叶子节点,是只为空(NIL或null)的节点。 第二,特性(5),确保没有一条路径会比其他路径长出俩倍。因而,红黑树是相对是接近平衡的二叉树。
红黑树示意图如下:
红黑树的基本操作是添加、删除和旋转。在对红黑树进行添加或删除后,会用到旋转方法。为什么呢?道理很简单,添加或删除红黑树中的节点之后,红黑树就发生了变化,可能不满足红黑树的5条性质,也就不再是一颗红黑树了,而是一颗普通的树。而通过旋转,可以使这颗树重新成为红黑树。简单点说,旋转的目的是让树保持红黑树的特性。 旋转包括两种:左旋 和 右旋。下面分别对红黑树的基本操作进行介绍。
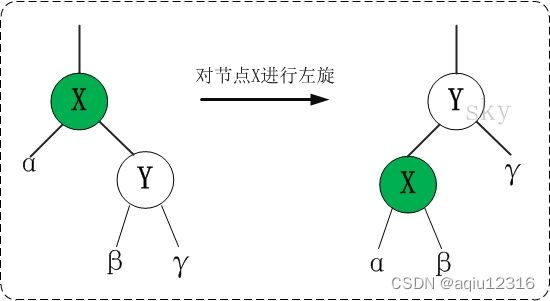
1.左旋
对x进行左旋,意味着"将x变成一个左节点"。
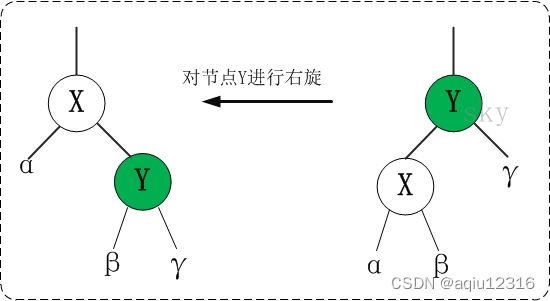
2. 右旋
对y进行左旋,意味着"将y变成一个右节点"。
3. 基本定义
RBTree是红黑树对应的类,RBTNode是红黑树的节点类。在RBTree中包含了根节点mRoot和红黑树的相关API。 注意:在实现红黑树API的过程中,我重载了许多函数。重载的原因,一是因为有的API是内部接口,有的是外部接口;二是为了让结构更加清晰。
public class RBTree> {
private RBTNode mRoot; // 根结点
private static final boolean RED = false;
private static final boolean BLACK = true;
public class RBTNode> {
boolean color; // 颜色
T key; // 关键字(键值)
RBTNode left; // 左孩子
RBTNode right; // 右孩子
RBTNode parent; // 父结点
public RBTNode(T key, boolean color, RBTNode parent, RBTNode left, RBTNode right) {
this.key = key;
this.color = color;
this.parent = parent;
this.left = left;
this.right = right;
}
}
...
}
4. 添加
将一个节点插入到红黑树中,需要执行哪些步骤呢?首先,将红黑树当作一颗二叉查找树,将节点插入;然后,将节点着色为红色;最后,通过"旋转和重新着色"等一系列操作来修正该树,使之重新成为一颗红黑树。详细描述如下: 第一步: 将红黑树当作一颗二叉查找树,将节点插入。 红黑树本身就是一颗二叉查找树,将节点插入后,该树仍然是一颗二叉查找树。也就意味着,树的键值仍然是有序的。此外,无论是左旋还是右旋,若旋转之前这棵树是二叉查找树,旋转之后它一定还是二叉查找树。这也就意味着,任何的旋转和重新着色操作,都不会改变它仍然是一颗二叉查找树的事实。 好吧?那接下来,我们就来想方设法的旋转以及重新着色,使这颗树重新成为红黑树!
第二步:将插入的节点着色为"红色"。 为什么着色成红色,而不是黑色呢?为什么呢?在回答之前,我们需要重新温习一下红黑树的特性: (1) 每个节点或者是黑色,或者是红色。 (2) 根节点是黑色。 (3) 每个叶子节点是黑色。 [注意:这里叶子节点,是指为空的叶子节点!] (4) 如果一个节点是红色的,则它的子节点必须是黑色的。 (5) 从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。 将插入的节点着色为红色,不会违背"特性(5)"!少违背一条特性,就意味着我们需要处理的情况越少。接下来,就要努力的让这棵树满足其它性质即可;满足了的话,它就又是一颗红黑树了。o(∩∩)o...哈哈
第三步: 通过一系列的旋转或着色等操作,使之重新成为一颗红黑树。 第二步中,将插入节点着色为"红色"之后,不会违背"特性(5)"。那它到底会违背哪些特性呢? 对于"特性(1)",显然不会违背了。因为我们已经将它涂成红色了。 对于"特性(2)",显然也不会违背。在第一步中,我们是将红黑树当作二叉查找树,然后执行的插入操作。而根据二叉查找数的特点,插入操作不会改变根节点。所以,根节点仍然是黑色。 对于"特性(3)",显然不会违背了。这里的叶子节点是指的空叶子节点,插入非空节点并不会对它们造成影响。 对于"特性(4)",是有可能违背的! 那接下来,想办法使之"满足特性(4)",就可以将树重新构造成红黑树了。
添加操作的实现代码(Java语言)
/*
* 将结点插入到红黑树中
*
* 参数说明:
* node 插入的结点 // 对应《算法导论》中的node
*/
private void insert(RBTNode node) {
int cmp;
RBTNode y = null;
RBTNode x = this.mRoot;
// 1. 将红黑树当作一颗二叉查找树,将节点添加到二叉查找树中。
while (x != null) {
y = x;
cmp = node.key.compareTo(x.key);
if (cmp < 0)
x = x.left;
else
x = x.right;
}
node.parent = y;
if (y!=null) {
cmp = node.key.compareTo(y.key);
if (cmp < 0)
y.left = node;
else
y.right = node;
} else {
this.mRoot = node;
}
// 2. 设置节点的颜色为红色
node.color = RED;
// 3. 将它重新修正为一颗二叉查找树
insertFixUp(node);
}
/*
* 新建结点(key),并将其插入到红黑树中
*
* 参数说明:
* key 插入结点的键值
*/
public void insert(T key) {
RBTNode node=new RBTNode(key,BLACK,null,null,null);
// 如果新建结点失败,则返回。
if (node != null)
insert(node);
}
内部接口 -- insert(node)的作用是将"node"节点插入到红黑树中。 外部接口 -- insert(key)的作用是将"key"添加到红黑树中。
添加修正操作的实现代码(Java语言)
/*
* 红黑树插入修正函数
*
* 在向红黑树中插入节点之后(失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* node 插入的结点 // 对应《算法导论》中的z
*/
private void insertFixUp(RBTNode node) {
RBTNode parent, gparent;
// 若“父节点存在,并且父节点的颜色是红色”
while (((parent = parentOf(node))!=null) && isRed(parent)) {
gparent = parentOf(parent);
//若“父节点”是“祖父节点的左孩子”
if (parent == gparent.left) {
// Case 1条件:叔叔节点是红色
RBTNode uncle = gparent.right;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2条件:叔叔是黑色,且当前节点是右孩子
if (parent.right == node) {
RBTNode tmp;
leftRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是左孩子。
setBlack(parent);
setRed(gparent);
rightRotate(gparent);
} else { //若“z的父节点”是“z的祖父节点的右孩子”
// Case 1条件:叔叔节点是红色
RBTNode uncle = gparent.left;
if ((uncle!=null) && isRed(uncle)) {
setBlack(uncle);
setBlack(parent);
setRed(gparent);
node = gparent;
continue;
}
// Case 2条件:叔叔是黑色,且当前节点是左孩子
if (parent.left == node) {
RBTNode tmp;
rightRotate(parent);
tmp = parent;
parent = node;
node = tmp;
}
// Case 3条件:叔叔是黑色,且当前节点是右孩子。
setBlack(parent);
setRed(gparent);
leftRotate(gparent);
}
}
// 将根节点设为黑色
setBlack(this.mRoot);
}
insertFixUp(node)的作用是对应"上面所讲的第三步"。它是一个内部接口。
5. 删除操作
将红黑树内的某一个节点删除。需要执行的操作依次是:首先,将红黑树当作一颗二叉查找树,将该节点从二叉查找树中删除;然后,通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。详细描述如下: 第一步:将红黑树当作一颗二叉查找树,将节点删除。 这和"删除常规二叉查找树中删除节点的方法是一样的"。分3种情况: ① 被删除节点没有儿子,即为叶节点。那么,直接将该节点删除就OK了。 ② 被删除节点只有一个儿子。那么,直接删除该节点,并用该节点的唯一子节点顶替它的位置。 ③ 被删除节点有两个儿子。那么,先找出它的后继节点;然后把“它的后继节点的内容”复制给“该节点的内容”;之后,删除“它的后继节点”。在这里,后继节点相当于替身,在将后继节点的内容复制给"被删除节点"之后,再将后继节点删除。这样就巧妙的将问题转换为"删除后继节点"的情况了,下面就考虑后继节点。 在"被删除节点"有两个非空子节点的情况下,它的后继节点不可能是双子非空。既然"的后继节点"不可能双子都非空,就意味着"该节点的后继节点"要么没有儿子,要么只有一个儿子。若没有儿子,则按"情况① "进行处理;若只有一个儿子,则按"情况② "进行处理。
第二步:通过"旋转和重新着色"等一系列来修正该树,使之重新成为一棵红黑树。 因为"第一步"中删除节点之后,可能会违背红黑树的特性。所以需要通过"旋转和重新着色"来修正该树,使之重新成为一棵红黑树。
删除操作的实现代码(Java语言)
/*
* 删除结点(node),并返回被删除的结点
*
* 参数说明:
* node 删除的结点
*/
private void remove(RBTNode node) {
RBTNode child, parent;
boolean color;
// 被删除节点的"左右孩子都不为空"的情况。
if ( (node.left!=null) && (node.right!=null) ) {
// 被删节点的后继节点。(称为"取代节点")
// 用它来取代"被删节点"的位置,然后再将"被删节点"去掉。
RBTNode replace = node;
// 获取后继节点
replace = replace.right;
while (replace.left != null)
replace = replace.left;
// "node节点"不是根节点(只有根节点不存在父节点)
if (parentOf(node)!=null) {
if (parentOf(node).left == node)
parentOf(node).left = replace;
else
parentOf(node).right = replace;
} else {
// "node节点"是根节点,更新根节点。
this.mRoot = replace;
}
// child是"取代节点"的右孩子,也是需要"调整的节点"。
// "取代节点"肯定不存在左孩子!因为它是一个后继节点。
child = replace.right;
parent = parentOf(replace);
// 保存"取代节点"的颜色
color = colorOf(replace);
// "被删除节点"是"它的后继节点的父节点"
if (parent == node) {
parent = replace;
} else {
// child不为空
if (child!=null)
setParent(child, parent);
parent.left = child;
replace.right = node.right;
setParent(node.right, replace);
}
replace.parent = node.parent;
replace.color = node.color;
replace.left = node.left;
node.left.parent = replace;
if (color == BLACK)
removeFixUp(child, parent);
node = null;
return ;
}
if (node.left !=null) {
child = node.left;
} else {
child = node.right;
}
parent = node.parent;
// 保存"取代节点"的颜色
color = node.color;
if (child!=null)
child.parent = parent;
// "node节点"不是根节点
if (parent!=null) {
if (parent.left == node)
parent.left = child;
else
parent.right = child;
} else {
this.mRoot = child;
}
if (color == BLACK)
removeFixUp(child, parent);
node = null;
}
/*
* 删除结点(z),并返回被删除的结点
*
* 参数说明:
* tree 红黑树的根结点
* z 删除的结点
*/
public void remove(T key) {
RBTNode node;
if ((node = search(mRoot, key)) != null)
remove(node);
}
内部接口 -- remove(node)的作用是将"node"节点插入到红黑树中。 外部接口 -- remove(key)删除红黑树中键值为key的节点。
删除修正操作的实现代码(Java语言)
/*
* 红黑树删除修正函数
*
* 在从红黑树中删除插入节点之后(红黑树失去平衡),再调用该函数;
* 目的是将它重新塑造成一颗红黑树。
*
* 参数说明:
* node 待修正的节点
*/
private void removeFixUp(RBTNode node, RBTNode parent) {
RBTNode other;
while ((node==null || isBlack(node)) && (node != this.mRoot)) {
if (parent.left == node) {
other = parent.right;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
setBlack(other);
setRed(parent);
leftRotate(parent);
other = parent.right;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.right==null || isBlack(other.right)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
setBlack(other.left);
setRed(other);
rightRotate(other);
other = parent.right;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.right);
leftRotate(parent);
node = this.mRoot;
break;
}
} else {
other = parent.left;
if (isRed(other)) {
// Case 1: x的兄弟w是红色的
setBlack(other);
setRed(parent);
rightRotate(parent);
other = parent.left;
}
if ((other.left==null || isBlack(other.left)) &&
(other.right==null || isBlack(other.right))) {
// Case 2: x的兄弟w是黑色,且w的俩个孩子也都是黑色的
setRed(other);
node = parent;
parent = parentOf(node);
} else {
if (other.left==null || isBlack(other.left)) {
// Case 3: x的兄弟w是黑色的,并且w的左孩子是红色,右孩子为黑色。
setBlack(other.right);
setRed(other);
leftRotate(other);
other = parent.left;
}
// Case 4: x的兄弟w是黑色的;并且w的右孩子是红色的,左孩子任意颜色。
setColor(other, colorOf(parent));
setBlack(parent);
setBlack(other.left);
rightRotate(parent);
node = this.mRoot;
break;
}
}
}
if (node!=null)
setBlack(node);
}
removeFixup(node, parent)是对应"上面所讲的第三步"。它是一个内部接口。
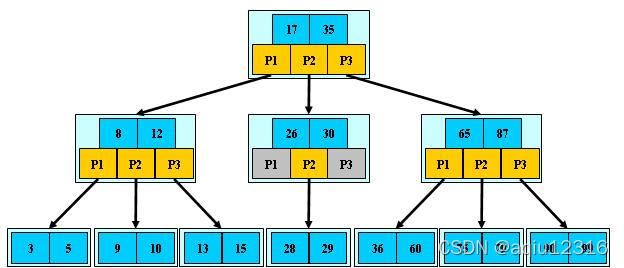
(4)B树
定义
在计算机科学中,B树(英语:B-tree)是一种自平衡的树,能够保持数据有序。这种数据结构能够让查找数据、顺序访问、插入数据及删除的动作,都在对数时间内完成。
为什么要引入B树?
首先,包括前面我们介绍的红黑树是将输入存入内存的一种内部查找树。
而B树是前面平衡树算法的扩展,它支持保存在磁盘或者网络上的符号表进行外部查找,这些文件可能比我们以前考虑的输入要大的多(难以存入内存)。
既然内容保存在磁盘中,那么自然会因为树的深度过大而造成磁盘I/O读写过于频繁(磁盘读写速率是有限制的),进而导致查询效率低下。
那么降低树的深度自然很重要了。因此,我们引入了B树,多路查找树。
特点
树中每个结点最多含有m个孩子(m>=2);
除根结点和叶子结点外,其它每个结点至少有[ceil(m / 2)]个孩子(其中ceil(x)是一个取上限的函数);
若根结点不是叶子结点,则至少有2个孩子(特殊情况:没有孩子的根结点,即根结点为叶子结点,整棵树只有一个根节点);
所有叶子结点都出现在同一层(最底层),叶子结点为外部结点,保存内容,即key和value。
其他结点为内部结点,保存索引,即key和next。
内部结点的关键字key:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
内容结点的指针next:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
例如:(M=3)
java代码实现
public class BTree, Value>
{
// max children per B-tree node = M-1
// (must be even and greater than 2)
private static final int M = 4;
private Node root; // root of the B-tree
private int height; // height of the B-tree
private int n; // number of key-value pairs in the B-tree
// helper B-tree node data type
private static final class Node
{
private int m; // number of children
private Entry[] children = new Entry[M]; // the array of children
// create a node with k children
private Node(int k)
{
m = k;
}
}
// internal nodes: only use key and next
// external nodes: only use key and value
private static class Entry
{
private Comparable key;
private Object val;
private Node next; // helper field to iterate over array entries
public Entry(Comparable key, Object val, Node next)
{
this.key = key;
this.val = val;
this.next = next;
}
}
/**
* Initializes an empty B-tree.
*/
public BTree()
{
root = new Node(0);
}
/**
* Returns true if this symbol table is empty.
* @return {@code true} if this symbol table is empty; {@code false} otherwise
*/
public boolean isEmpty()
{
return size() == 0;
}
/**
* Returns the number of key-value pairs in this symbol table.
* @return the number of key-value pairs in this symbol table
*/
public int size()
{
return n;
}
/**
* Returns the height of this B-tree (for debugging).
*
* @return the height of this B-tree
*/
public int height()
{
return height;
}
/**
* Returns the value associated with the given key.
*
* @param key the key
* @return the value associated with the given key if the key is in the symbol table
* and {@code null} if the key is not in the symbol table
* @throws NullPointerException if {@code key} is {@code null}
*/
public Value get(Key key)
{
if (key == null)
{
throw new NullPointerException("key must not be null");
}
return search(root, key, height);
}
@SuppressWarnings("unchecked")
private Value search(Node x, Key key, int ht)
{
Entry[] children = x.children;
// external node到最底层叶子结点,遍历
if (ht == 0)
{
for (int j = 0; j < x.m; j++)
{
if (eq(key, children[j].key))
{
return (Value) children[j].val;
}
}
}
// internal node递归查找next地址
else
{
for (int j = 0; j < x.m; j++)
{
if (j+1 == x.m || less(key, children[j+1].key))
{
return search(children[j].next, key, ht-1);
}
}
}
return null;
}
/**
* Inserts the key-value pair into the symbol table, overwriting the old value
* with the new value if the key is already in the symbol table.
* If the value is {@code null}, this effectively deletes the key from the symbol table.
*
* @param key the key
* @param val the value
* @throws NullPointerException if {@code key} is {@code null}
*/
public void put(Key key, Value val)
{
if (key == null)
{
throw new NullPointerException("key must not be null");
}
Node u = insert(root, key, val, height); //分裂后生成的右结点
n++;
if (u == null)
{
return;
}
// need to split root重组root
Node t = new Node(2);
t.children[0] = new Entry(root.children[0].key, null, root);
t.children[1] = new Entry(u.children[0].key, null, u);
root = t;
height++;
}
private Node insert(Node h, Key key, Value val, int ht)
{
int j;
Entry t = new Entry(key, val, null);
// external node外部结点,也是叶子结点,在树的最底层,存的是内容value
if (ht == 0)
{
for (j = 0; j < h.m; j++)
{
if (less(key, h.children[j].key))
{
break;
}
}
}
// internal node内部结点,存的是next地址
else
{
for (j = 0; j < h.m; j++)
{
if ((j+1 == h.m) || less(key, h.children[j+1].key))
{
Node u = insert(h.children[j++].next, key, val, ht-1);
if (u == null)
{
return null;
}
t.key = u.children[0].key;
t.next = u;
break;
}
}
}
for (int i = h.m; i > j; i--)
{
h.children[i] = h.children[i-1];
}
h.children[j] = t;
h.m++;
if (h.m < M)
{
return null;
}
else
{ //分裂结点
return split(h);
}
}
// split node in half
private Node split(Node h)
{
Node t = new Node(M/2);
h.m = M/2;
for (int j = 0; j < M/2; j++)
{
t.children[j] = h.children[M/2+j];
}
return t;
}
/**
* Returns a string representation of this B-tree (for debugging).
*
* @return a string representation of this B-tree.
*/
public String toString()
{
return toString(root, height, "") + "\n";
}
private String toString(Node h, int ht, String indent)
{
StringBuilder s = new StringBuilder();
Entry[] children = h.children;
if (ht == 0)
{
for (int j = 0; j < h.m; j++)
{
s.append(indent + children[j].key + " " + children[j].val + "\n");
}
}
else
{
for (int j = 0; j < h.m; j++)
{
if (j > 0)
{
s.append(indent + "(" + children[j].key + ")\n");
}
s.append(toString(children[j].next, ht-1, indent + " "));
}
}
return s.toString();
}
// comparison functions - make Comparable instead of Key to avoid casts
private boolean less(Comparable k1, Comparable k2)
{
return k1.compareTo(k2) < 0;
}
private boolean eq(Comparable k1, Comparable k2)
{
return k1.compareTo(k2) == 0;
}
/**
* Unit tests the {@code BTree} data type.
*
* @param args the command-line arguments
*/
public static void main(String[] args)
{
BTree st = new BTree();
st.put("www.cs.princeton.edu", "128.112.136.12");
st.put("www.cs.princeton.edu", "128.112.136.11");
st.put("www.princeton.edu", "128.112.128.15");
st.put("www.yale.edu", "130.132.143.21");
st.put("www.simpsons.com", "209.052.165.60");
st.put("www.apple.com", "17.112.152.32");
st.put("www.amazon.com", "207.171.182.16");
st.put("www.ebay.com", "66.135.192.87");
st.put("www.cnn.com", "64.236.16.20");
st.put("www.google.com", "216.239.41.99");
st.put("www.nytimes.com", "199.239.136.200");
st.put("www.microsoft.com", "207.126.99.140");
st.put("www.dell.com", "143.166.224.230");
st.put("www.slashdot.org", "66.35.250.151");
st.put("www.espn.com", "199.181.135.201");
st.put("www.weather.com", "63.111.66.11");
st.put("www.yahoo.com", "216.109.118.65");
System.out.println("cs.princeton.edu: " + st.get("www.cs.princeton.edu"));
System.out.println("hardvardsucks.com: " + st.get("www.harvardsucks.com"));
System.out.println("simpsons.com: " + st.get("www.simpsons.com"));
System.out.println("apple.com: " + st.get("www.apple.com"));
System.out.println("ebay.com: " + st.get("www.ebay.com"));
System.out.println("dell.com: " + st.get("www.dell.com"));
System.out.println();
System.out.println("size: " + st.size());
System.out.println("height: " + st.height());
System.out.println(st);
System.out.println();
}
}
(5)哈夫曼树(Huffman Tree)
哈夫曼树(霍夫曼树)又称为最优树.
1、路径和路径长度 在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长
2、结点的权及带权路径长度 若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度 树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
树节点:
/**
* 树节点
*
* @author pang
*
* @param
*/
public class Node implements Comparable> {
private T data;
private int weight;
private Node left;
private Node right;
public Node(T data, int weight) {
this.data = data;
this.weight = weight;
}
@Override
public String toString() {
// TODO Auto-generated method stub
return "data:" + this.data + ",weight:" + this.weight + "; ";
}
@Override
public int compareTo(Node o) {
// TODO Auto-generated method stub
if (o.weight > this.weight) {
return 1;
} else if (o.weight < this.weight) {
return -1;
}
return 0;
}
public T getData() {
return data;
}
public void setData(T data) {
this.data = data;
}
public int getWeight() {
return weight;
}
public void setWeight(int weight) {
this.weight = weight;
}
public Node getLeft() {
return left;
}
public void setLeft(Node left) {
this.left = left;
}
public Node getRight() {
return right;
}
public void setRight(Node right) {
this.right = right;
}
}
HuffmanTree:
import java.util.ArrayList;
import java.util.Collections;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;
public class HuffmanTree {
public static Node createTree(List> nodes) {
while (nodes.size() > 1) {
Collections.sort(nodes);
Node left = nodes.get(nodes.size() - 1);
Node right = nodes.get(nodes.size() - 2);
Node parent = new Node(null, left.getWeight()
+ right.getWeight());
parent.setLeft(left);
parent.setRight(right);
nodes.remove(left);
nodes.remove(right);
nodes.add(parent);
}
return nodes.get(0);
}
public static List> breath(Node root) {
List> list = new ArrayList>();
Queue> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node pNode = queue.poll();
list.add(pNode);
if (pNode.getLeft() != null) {
queue.add(pNode.getLeft());
}
if (pNode.getRight() != null) {
queue.add(pNode.getRight());
}
}
return list;
}
}
(6)树的遍历
二叉树遍历分为前序、中序、后序递归和非递归遍历、还有层序遍历。
//二叉树节点
public class BinaryTreeNode {
private int data;
private BinaryTreeNode left;
private BinaryTreeNode right;
public BinaryTreeNode() {}
public BinaryTreeNode(int data, BinaryTreeNode left, BinaryTreeNode right) {
super();
this.data = data;
this.left = left;
this.right = right;
}
public int getData() {
return data;
}
public void setData(int data) {
this.data = data;
}
public BinaryTreeNode getLeft() {
return left;
}
public void setLeft(BinaryTreeNode left) {
this.left = left;
}
public BinaryTreeNode getRight() {
return right;
}
public void setRight(BinaryTreeNode right) {
this.right = right;
}
}
前序递归遍历算法:访问根结点-->递归遍历根结点的左子树-->递归遍历根结点的右子树
中序递归遍历算法:递归遍历根结点的左子树-->访问根结点-->递归遍历根结点的右子树
后序递归遍历算法:递归遍历根结点的左子树-->递归遍历根结点的右子树-->访问根结点
import com.ccut.aaron.stack.LinkedStack;
public class BinaryTree {
//前序遍历递归的方式
public void preOrder(BinaryTreeNode root){
if(null!=root){
System.out.print(root.getData()+"\t");
preOrder(root.getLeft());
preOrder(root.getRight());
}
}
//前序遍历非递归的方式
public void preOrderNonRecursive(BinaryTreeNode root){
Stack stack=new Stack();
while(true){
while(root!=null){
System.out.print(root.getData()+"\t");
stack.push(root);
root=root.getLeft();
}
if(stack.isEmpty()) break;
root=stack.pop();
root=root.getRight();
}
}
//中序遍历采用递归的方式
public void inOrder(BinaryTreeNode root){
if(null!=root){
inOrder(root.getLeft());
System.out.print(root.getData()+"\t");
inOrder(root.getRight());
}
}
//中序遍历采用非递归的方式
public void inOrderNonRecursive(BinaryTreeNode root){
Stack stack=new Stack();
while(true){
while(root!=null){
stack.push(root);
root=root.getLeft();
}
if(stack.isEmpty())break;
root=stack.pop();
System.out.print(root.getData()+"\t");
root=root.getRight();
}
}
//后序遍历采用递归的方式
public void postOrder(BinaryTreeNode root){
if(root!=null){
postOrder(root.getLeft());
postOrder(root.getRight());
System.out.print(root.getData()+"\t");
}
}
//后序遍历采用非递归的方式
public void postOrderNonRecursive(BinaryTreeNode root){
Stack stack=new Stack();
while(true){
if(root!=null){
stack.push(root);
root=root.getLeft();
}else{
if(stack.isEmpty()) return;
if(null==stack.lastElement().getRight()){
root=stack.pop();
System.out.print(root.getData()+"\t");
while(root==stack.lastElement().getRight()){
System.out.print(stack.lastElement().getData()+"\t");
root=stack.pop();
if(stack.isEmpty()){
break;
}
}
}
if(!stack.isEmpty())
root=stack.lastElement().getRight();
else
root=null;
}
}
}
//层序遍历
public void levelOrder(BinaryTreeNode root){
BinaryTreeNode temp;
Queue queue=new LinkedList();
queue.offer(root);
while(!queue.isEmpty()){
temp=queue.poll();
System.out.print(temp.getData()+"\t");
if(null!=temp.getLeft())
queue.offer(temp.getLeft());
if(null!=temp.getRight()){
queue.offer(temp.getRight());
}
}
}
public static void main(String[] args) {
BinaryTreeNode node10=new BinaryTreeNode(10,null,null);
BinaryTreeNode node8=new BinaryTreeNode(8,null,null);
BinaryTreeNode node9=new BinaryTreeNode(9,null,node10);
BinaryTreeNode node4=new BinaryTreeNode(4,null,null);
BinaryTreeNode node5=new BinaryTreeNode(5,node8,node9);
BinaryTreeNode node6=new BinaryTreeNode(6,null,null);
BinaryTreeNode node7=new BinaryTreeNode(7,null,null);
BinaryTreeNode node2=new BinaryTreeNode(2,node4,node5);
BinaryTreeNode node3=new BinaryTreeNode(3,node6,node7);
BinaryTreeNode node1=new BinaryTreeNode(1,node2,node3);
BinaryTree tree=new BinaryTree();
//采用递归的方式进行遍历
System.out.println("-----前序遍历------");
tree.preOrder(node1);
System.out.println();
//采用非递归的方式遍历
tree.preOrderNonRecursive(node1);
System.out.println();
//采用递归的方式进行遍历
System.out.println("-----中序遍历------");
tree.inOrder(node1);
System.out.println();
//采用非递归的方式遍历
tree.inOrderNonRecursive(node1);
System.out.println();
//采用递归的方式进行遍历
System.out.println("-----后序遍历------");
tree.postOrder(node1);
System.out.println();
//采用非递归的方式遍历
tree.postOrderNonRecursive(node1);
System.out.println();
//采用递归的方式进行遍历
System.out.println("-----层序遍历------");
tree.levelOrder(node1);
System.out.println();
}
}
4,哈希表(散列表)
哈希表的结构是由数组+链表或者数组+二叉树组成,实现的思路是创建一个固定大小的链表数组,将各条链表交给数组来进行管理,根据自定义的规则,将数据依次插入链表中,这样查找起来会非常方便。
package cn.mrlij.hash;
import java.util.Scanner;
public class HashTableDemo {
public static void main(String[] args) {
// 创建Hashtab
HashTable ht = new HashTable(7);
String key = "";
Scanner sc = new Scanner(System.in);
while (true) {
System.out.println("添加雇员:add");
System.out.println("遍历雇员:list");
System.out.println("查找雇员:get");
System.out.println("删除雇员:del");
System.out.println("退出:exit");
key = sc.next();
switch (key) {
case "add":
System.out.println("输入id");
int id = sc.nextInt();
System.out.println("输入姓名");
String name = sc.next();
Emp emp = new Emp(id, name);
ht.add(emp);
break;
case "list":
ht.list();
break;
case "exit":
System.out.println("退出系统!");
sc.close();
System.exit(0);
case "get":
System.out.println("请输入id");
int no = sc.nextInt();
ht.findById(no);
break;
case "del":
System.out.println("请输入要删除员工的Id");
int eid = sc.nextInt();
ht.del(eid);
break;
default:
System.out.println("输入错误!");
break;
}
}
}
}
//创建hash表,管理多条链表
class HashTable {
private EmpLinkedList[] arr;
private int size;
// 初始化构造器
public HashTable(int size) {
// 创建大小为7的数组
arr = new EmpLinkedList[size];
this.size = size;
// 除了初始化数组,还需要初始化链表
for (int i = 0; i < size; i++) {
arr[i] = new EmpLinkedList();
}
}
// 添加员工
public void add(Emp emp) {
// 根据散列函数确定员工编号应该放在哪条链表上面
int hashFun = hashFun(emp.id);
arr[hashFun].add(emp);
}
// 自定义散列函数
public int hashFun(int id) {
return id % size;
}
// 遍历哈希表
public void list() {
for (int i = 0; i < size; i++) {
arr[i].list(i);
}
}
//根据id删除员工
public void del(int no) {
int id = hashFun(no);
arr[id].del(no);
}
// 根据Id查找雇员
public void findById(int id) {
int hashFun = hashFun(id);
Emp emp = arr[hashFun].findById(id);
if (emp == null) {
System.out.println("没有该员工!");
} else {
System.out.printf("员工id:%d,姓名:%s", emp.id, emp.name);
}
}
}
//创建一个雇员
class Emp {
public int id;
public String name;
public Emp next;
public Emp(int id, String name) {
this.id = id;
this.name = name;
}
}
//创建一个链表类,封装增删改查方法
class EmpLinkedList {
// 创建一个头结点,直接指向第一个Emp
private Emp head;// 默认为null
// 根据雇员ID查找
public Emp findById(int id) {
// 当头结点为空时,说明链表为空!
if (head == null) {
return null;
}
Emp temp = head;
while (true) {
// 找到ID
if (temp.id == id) {
break;
}
// 链表遍历完毕没有找到
if (temp.next == null) {
temp = null;
break;
}
temp = temp.next;
}
return temp;
}
/*
* 添加雇员
*/
public void add(Emp emp) {
// 如果是添加的是第一个雇员,将头结点直接指向当前添加的节点
if (head == null) {
head = emp;
return;
}
Emp temp = head;// 定义辅助节点
// 不是第一个节点,遍历链表,将待添加的节点放在最后一个节点的后面
// 循环遍历找到最后一个节点
while (true) {
if (temp.next == null) {
break;
}
temp = temp.next;
}
// 将添加的节点放在找到的最后节点的后面
temp.next = emp;
}
// 遍历节点
public void list(int no) {
if (head == null) {
System.out.println("第" + (no + 1) + "链表为空!");
return;
}
Emp temp = head;// 定义辅助节点,用于遍历
while (true) {
System.out.printf("第" + (no + 1) + "链表的id是%d,姓名是%s\t", temp.id, temp.name);
if (temp.next == null) {
break;
}
temp = temp.next;
}
System.out.println();
}
// 删除雇员
public void del(int no) {
if(head == null) {
System.out.println("该链表为空!");
return;
}
// 当头结点的id等于要查找的id,直接删除
if (head.id == no) {
head = head.next;
return;
}
Emp temp = head;// 定义辅助节点
boolean flag = false;
while (true) {
if (temp.next == null) {
break;// 说明没有找到该点
}
if (temp.next.id == no) {
// 删除操作
flag = true;
break;
}
}
if (flag) {
// 找到该id,删除
temp.next = temp.next.next;
} else {
System.out.println("没有找到该员工!");
}
}
}
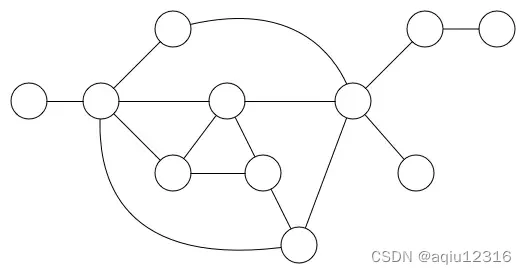
5,图
图看起来就像下图这样:
在计算机科学中,一个图就是一些顶点的集合,这些顶点通过一系列边结对(连接)。顶点用圆圈表示,边就是这些圆圈之间的连线。顶点之间通过边连接。
注意:顶点有时也称为节点或者交点,边有时也称为链接。
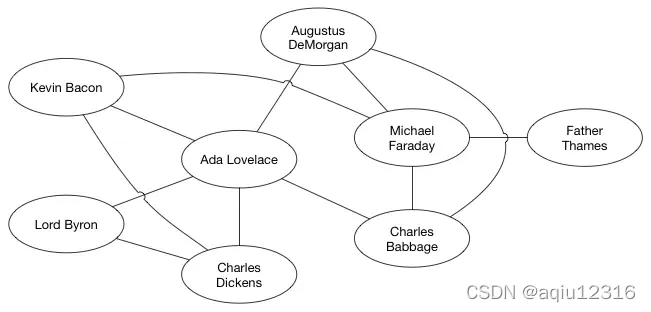
一个图可以表示一个社交网络,每一个人就是一个顶点,互相认识的人之间通过边联系。
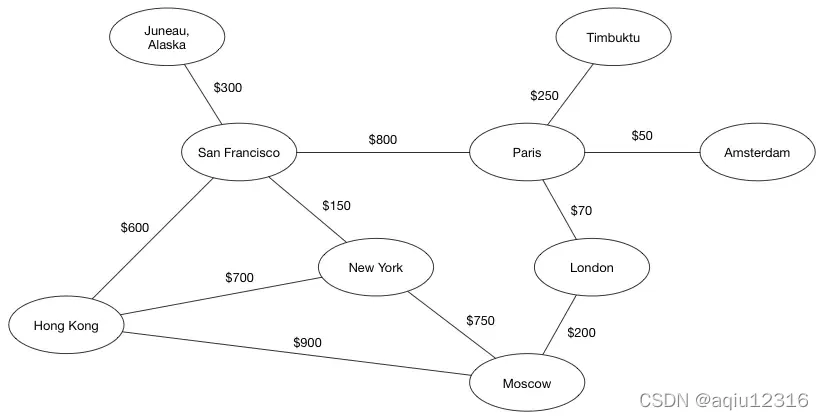
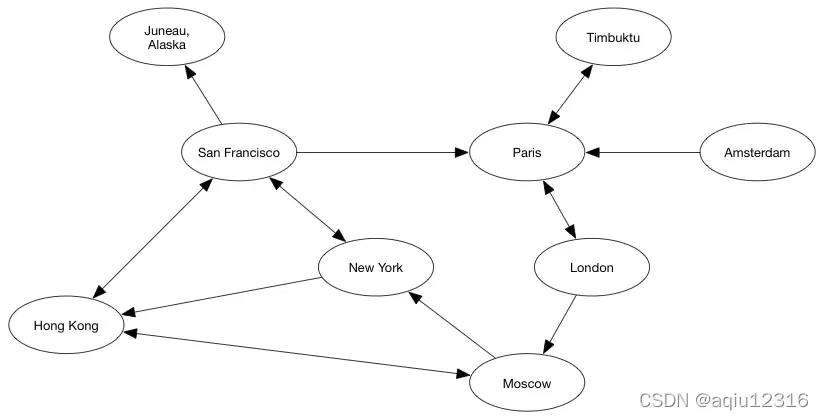
图有各种形状和大小。边可以有权重(weight),即每一条边会被分配一个正数或者负数值。考虑一个代表航线的图。各个城市就是顶点,航线就是边。那么边的权重可以是飞行时间,或者机票价格。
有了这样一张假设的航线图。从旧金山到莫斯科最便宜的路线是到纽约转机。
边可以是有方向的。在上面提到的例子中,边是没有方向的。例如,如果 Ada 认识 Charles,那么 Charles 也就认识 Ada。相反,有方向的边意味着是单方面的关系。一条从顶点 X 到 顶点 Y 的边是将 X 联向 Y,不是将 Y 联向 X。
继续前面航班的例子,从旧金山到阿拉斯加的朱诺有向边意味着从旧金山到朱诺有航班,但是从朱诺到旧金山没有(我假设那样意味着你需要走回去)。
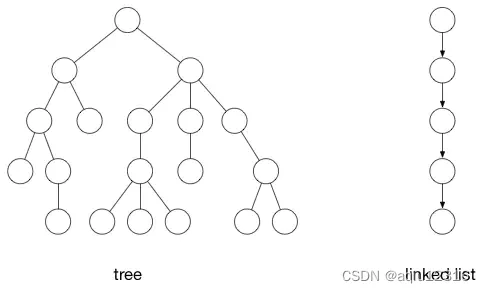
下面的两种情况也是属于图:
左边的是树,右边的是链表。他们都可以被当成是树,只不过是一种更简单的形式。他们都有顶点(节点)和边(连接)。
第一种图包含圈(cycles),即你可以从一个顶点出发,沿着一条路劲最终会回到最初的顶点。树是不包含圈的图。
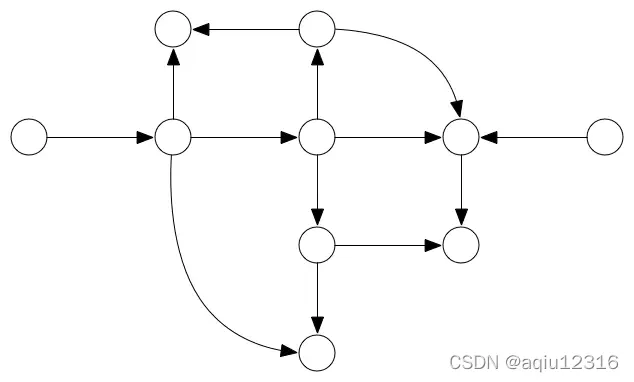
另一种常见的图类型是单向图或者 DAG:
就像树一样,这个图没有任何圈(无论你从哪一个节点出发,你都无法回到最初的节点),但是这个图有有向边(通过一个箭头表示,这里的箭头不表示继承关系)。
为什么要使用图?
也许你耸耸肩然后心里想着,有什么大不了的。好吧,事实证明图是一种有用的数据结构。
如果你有一个编程问题可以通过顶点和边表示出来,那么你就可以将你的问题用图画出来,然后使用著名的图算法(比如广度优先搜索 或者 深度优先搜索)来找到解决方案。
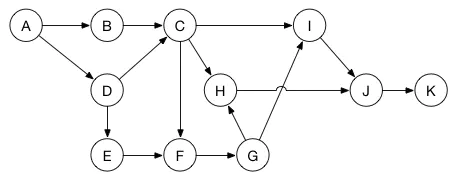
例如,假设你有一系列任务需要完成,但是有的任务必须等待其他任务完成后才可以开始。你可以通过非循环有向图来建立模型:
每一个顶点代表一个任务。两个任务之间的边表示目的任务必须等到源任务完成后才可以开始。比如,在任务B和任务D都完成之前,任务C不可以开始。在任务A完成之前,任务A和D都不能开始。
现在这个问题就通过图描述清楚了,你可以使用深度优先搜索算法来执行执行拓扑排序。这样就可以将所有的任务排入最优的执行顺序,保证等待任务完成的时间最小化。(这里可能的顺序之一是:A, B, D, E, C, F, G, H, I, J, K)
不管是什么时候遇到困难的编程问题,问一问自己:“如何用图来表述这个问题?”。图都是用于表示数据之间的关系。 诀窍在于如何定义“关系”。
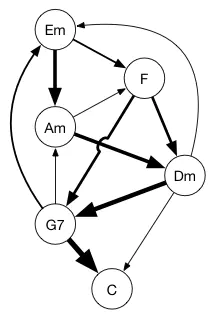
如果你是一个音乐家你可能会喜欢这个图:
这些顶点来自C大调的和弦。这些边--表示和弦之间的关系--描述了怎样从一个和弦到另一个和弦。这是一个有向图,所以箭头的方向表示了怎样从一个和弦到下一个和弦。它同时还是一个加权图,每一条边的权重(这里用线条的宽度来表示)说明了两个和弦之间的强弱关系。如你所见,G7-和弦后是一个C和弦和一个很轻的 Am 和弦。
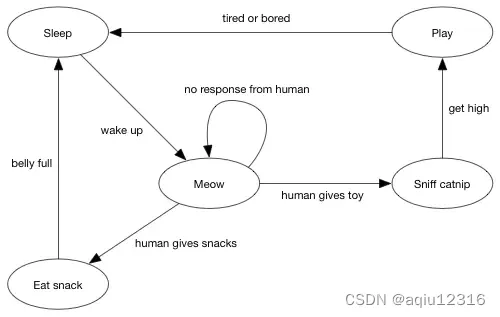
程序员常用的另一个图就是状态机,这里的边描述了状态之间切换的条件。下面这个状态机描述了一个猫的状态:
图真的很棒。Facebook 就从他们的社交图中赚取了巨额财富。如果计划学习任何数据结构,则应该选择图,以及大量的标准图算法。
顶点和边
理论上,图就是一堆顶点和边对象而已,但是怎么在代码中来描述呢?
有两种主要的方法:邻接列表和邻接矩阵。
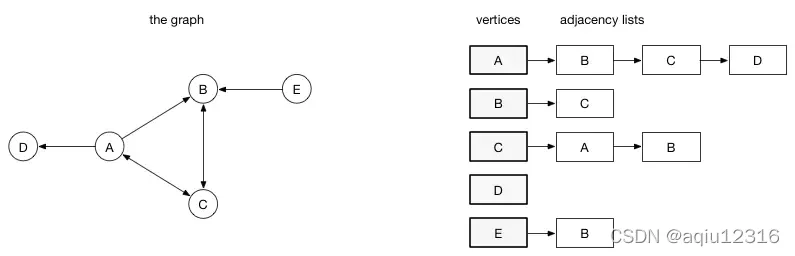
邻接列表:在邻接列表实现中,每一个顶点会存储一个从它这里开始的边的列表。比如,如果顶点A 有一条边到B、C和D,那么A的列表中会有3条边
邻接列表只描述了指向外部的边。A 有一条边到B,但是B没有边到A,所以 A没有出现在B的邻接列表中。查找两个顶点之间的边或者权重会比较费时,因为遍历邻接列表直到找到为止。
邻接矩阵:在邻接矩阵实现中,由行和列都表示顶点,由两个顶点所决定的矩阵对应元素表示这里两个顶点是否相连、如果相连这个值表示的是相连边的权重。例如,如果从顶点A到顶点B有一条权重为 5.6 的边,那么矩阵中第A行第B列的位置的元素值应该是5.6:
往这个图中添加顶点的成本非常昂贵,因为新的矩阵结果必须重新按照新的行/列创建,然后将已有的数据复制到新的矩阵中。
所以使用哪一个呢?大多数时候,选择邻接列表是正确的。下面是两种实现方法更详细的比较。
假设 V 表示图中顶点的个数,E 表示边的个数。
操作
邻接列表
邻接矩阵
存储空间
O(V + E)
O(V^2)
添加顶点
O(1)
O(V^2)
添加边
O(1)
O(1)
检查相邻性
O(V)
O(1)
“检查相邻性” 是指对于给定的顶点,尝试确定它是否是另一个顶点的邻居。在邻接列表中检查相邻性的时间复杂度是O(V),因为最坏的情况是一个顶点与每一个顶点都相连。
在 稀疏图的情况下,每一个顶点都只会和少数几个顶点相连,这种情况下相邻列表是最佳选择。如果这个图比较密集,每一个顶点都和大多数其他顶点相连,那么相邻矩阵更合适。
代码:顶点和边
先看一下边的定义:
class Edge(val from: Vertex,
val to: Vertex,
val weight: Double? = 0.toDouble()) {
}
边包含了3个属性 “from” 和 “to” 顶点,以及权重值。注意 Edge 对象总是有方向的。如果需要添加一条无向边,你需要在相反方向添加一个 Edge 对象。weight 属性是可选的,所以加权图和未加权图都可以用它们来描述。
Vertex 的定义:
class Vertex(var data: T? = null, var index: Int = 0) {
//val edgeList : List> = emptyList()
val edges: ArrayList> = ArrayList()
var visited = false
//var distance = 0
fun addEdge(edge: Edge){
edges.add(edge)
}
override fun toString(): String {
return data.toString()
}
}
由于是泛型定义,所以它可以存放任何类型的数据。
图
注意:图的实现方式有很多,这里给出来的只是一种可能的实现。你可以根据不同问题来裁剪这些代码。例如你的边可能不需要 weight 属性,你也可能不需要区分有向边和无向边。
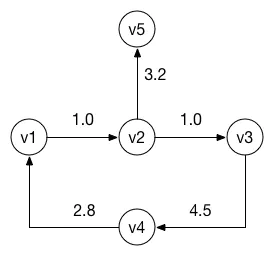
这里有一个简单的图:
我们可以用邻接列表或者邻接矩阵来实现。实现这些概念的类都是继承自通用的 API AbstractGraph,所以它们可以相同的方式创建,但是背后各自使用不同的数据结构。
我们来创建一个有向加权图,来存储上面的数据:
val graph = Graph()
val v1 = graph.createVertex(1)
val v2 = graph.createVertex(2)
val v3 = graph.createVertex(3)
val v4 = graph.createVertex(4)
val v5 = graph.createVertex(5)
graph.addDirectedEdge(fromVertex = v1, toVertex = v2, weightValue = 1.0)
graph.addDirectedEdge(fromVertex = v2, toVertex = v3, weightValue = 1.0)
graph.addDirectedEdge(fromVertex = v3, toVertex = v4, weightValue = 4.5)
graph.addDirectedEdge(fromVertex = v4, toVertex = v1, weightValue = 2.8)
graph.addDirectedEdge(fromVertex = v2, toVertex = v5, weightValue = 3.2)
graph.printAdjacencyList()
前面我们已经说过,如果要添加一条无向边,需要添加两条有向边。对于无向图,我们可以使用下面的代码来替换:
graph.addUnDirectedEdge(fromVertex = v1, toVertex = v2, weightValue = 1.0)
graph.addUnDirectedEdge(fromVertex = v2, toVertex = v3, weightValue = 1.0)
graph.addUnDirectedEdge(fromVertex = v3, toVertex = v4, weightValue = 4.5)
graph.addUnDirectedEdge(fromVertex = v4, toVertex = v1, weightValue = 2.8)
graph.addUnDirectedEdge(fromVertex = v2, toVertex = v5, weightValue = 3.2)
如果是未加权图,weight 这个参数我们可以不用传递值。
邻接列表的实现
为了维护邻接列表,需要一个类(EdgeList)将边列表映射到一个顶点。然后图只需要简单的维护这样一个对象(EdgeList)的列表就可以,并根据需要修改这个列表。
class EdgeList (var vertex: Vertex ){
var edges: ArrayList> = ArrayList()
fun addEdge(edge: Edge){
edges.add(edge)
}
}
Graph 的完整实现:
class Graph(private val vertices: ArrayList> = ArrayList(),
private val adjacencyList: ArrayList> = ArrayList()) {
fun createVertex(value: T): Vertex {
val matchingVertices = vertices.filter { it.data == value }
if (matchingVertices.isNotEmpty()) {
return matchingVertices.last()
}
val vertex = Vertex(value, adjacencyList.size)
vertices.add(vertex)
adjacencyList.add(EdgeList(vertex))
return vertex
}
fun addDirectedEdge(fromVertex: Vertex, toVertex: Vertex, weightValue: Double) {
val edge = Edge(from = fromVertex,
to = toVertex,
weight = weightValue)
fromVertex.addEdge(edge)
val fromIndex = vertices.indexOf(fromVertex)
adjacencyList[fromIndex].edges.add(edge)
}
fun addUnDirectedEdge(fromVertex: Vertex, toVertex: Vertex, weightValue: Double = 0.0) {
addDirectedEdge(fromVertex, toVertex, weightValue)
addDirectedEdge(toVertex, fromVertex, weightValue)
}
fun printAdjacencyList() {
(0 until vertices.size)
.filterNot { adjacencyList[it].edges.isEmpty() }
.forEach { println("""${vertices[it].data} ->[${adjacencyList[it].edges.joinToString()}] """) }
}
}
来测试一下上面的那个航线图:
val planeGraph = Graph()
val hk = planeGraph.createVertex("Hong Kong")
val ny = planeGraph.createVertex("New York")
val mosc = planeGraph.createVertex("Moscow")
val ld = planeGraph.createVertex("London")
val pairs = planeGraph.createVertex("Pairs")
val am = planeGraph.createVertex("Amsterdam")
val sf = planeGraph.createVertex("San Francisco")
val ja = planeGraph.createVertex("Juneau Alaska")
val tm = planeGraph.createVertex("Timbuktu")
planeGraph.addUnDirectedEdge(hk, sf, 500.0)
planeGraph.addUnDirectedEdge(hk,mosc,900.0)
planeGraph.addDirectedEdge(sf, ja, 300.0)
planeGraph.addUnDirectedEdge(sf, ny, 150.0)
planeGraph.addDirectedEdge(mosc,ny, 750.0)
planeGraph.addDirectedEdge(ld, mosc, 200.0)
planeGraph.addUnDirectedEdge(ld, pairs, 70.0)
planeGraph.addDirectedEdge(sf,pairs, 800.0)
planeGraph.addUnDirectedEdge(pairs, tm, 250.0)
planeGraph.addDirectedEdge(am, pairs, 50.0)
planeGraph.printAdjacencyList()
运行结果如下:
Hong Kong ->[(San Francisco: 500.0), (Moscow: 900.0)]
Moscow ->[(New York: 750.0)]
London ->[(Moscow: 200.0), (Pairs: 70.0)]
Pairs ->[(Timbuktu: 250.0)]
Amsterdam ->[(Pairs: 50.0)]
San Francisco ->[(Juneau Alaska: 300.0), (New York: 150.0), (Pairs: 800.0)]
最短路径
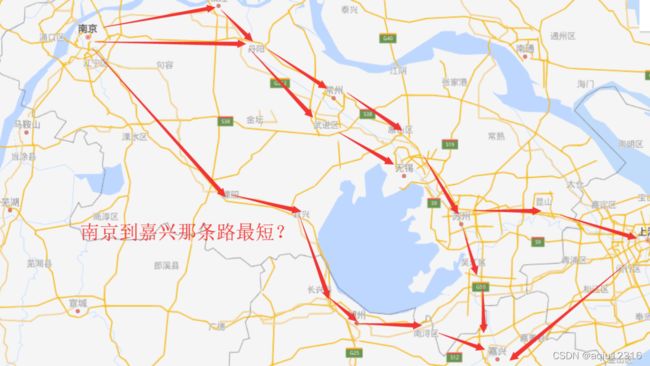
Dijkstra是用来求单源最短路径的
就拿上图来说,假如直到的路径和长度已知,那么可以使用dijkstra算法计算南京到图中所有节点的最短距离。
单源什么意思?
-
从一个顶点出发,Dijkstra算法只能求一个顶点到其他点的最短距离而不能任意两点。
和bfs求的最短路径有什么区别?
-
bfs求的与其说是路径,不如说是次数。因为bfs他是按照队列一次一次进行加入相邻的点,而两点之间没有权值或者权值相等(代价相同)。处理的更多是偏向迷宫类的这种都是只能走邻居(不排除特例)。
Dijkstra在处理具体实例的应用还是很多的,因为具体的问题其实带权更多一些。
比如一个城市有多个乡镇,乡镇可能有道路,也可能没有,整个乡镇联通,如果想计算每个乡镇到a镇的最短路径,那么Dijkstra就派上了用场。
算法分析
对于一个算法,首先要理解它的运行流程。 对于一个Dijkstra算法而言,前提是它的前提条件和环境:
-
一个连通图,若干节点,节点可能有数值,但是路径一定有权值。并且路径不能为负。否则Dijkstra就不适用。
Dijkstra的核心思想是贪心算法的思想。不懂贪心?
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。 贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
对于贪心算法,在很多情况都能用到。下面举几个不恰当的例子!
打个比方,吃自助餐,目标是吃回本,那么胃有限那么每次都仅最贵的吃。
上学时,麻麻说只能带5个苹果,你想带最多,那么选五个苹果你每次都选最大的那个五次下来你就选的最重的那个。
不难发现上面的策略虽然没有很强的理论数学依据,或者不太好说明。但是事实规律就是那样,并且对于贪心问题大部分都需要排序,还可能会遇到类排序。并且一个物体可能有多个属性,不同问题需要按照不同属性进行排序,操作。
那么我们的Dijkstra是如何贪心的呢?对于一个点,求图中所有点的最短路径,如果没有正确的方法胡乱想确实很难算出来,并且如果暴力匹配复杂度呈指数级上升不适合解决实际问题。
那么我们该怎么想呢?
Dijkstra算法的前提:
-
首先,Dijkstra处理的是带正权值的有权图,那么,就需要一个二维数组(如果空间大用list数组)存储各个点到达(边)的权值大小。(邻接矩阵或者邻接表存储)
-
其次,还需要一个boolean数组判断那些点已经确定最短长度,那些点没有确定。int数组记录距离(在算法执行过程可能被多次更新)。
-
需要优先队列加入已经确定点的周围点。每次抛出确定最短路径的那个并且确定最短,直到所有点路径确定最短为止。
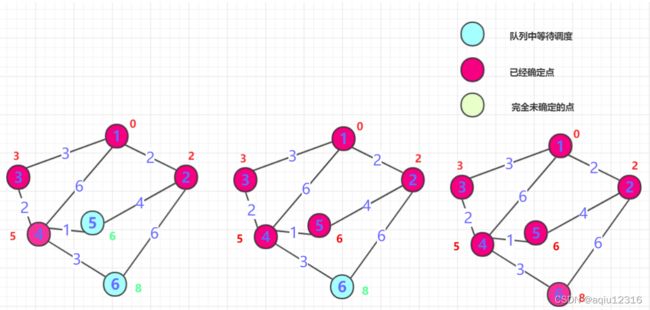
简单的概括流程为:
-
一般从选定点开始抛入优先队列。(路径一般为0),boolean数组标记0的位置(最短为0) , 然后0周围连通的点抛入优先队列中(可能是node类),并把各个点的距离记录到对应数组内(如果小于就更新,大于就不动,初始第一次是无穷肯定会更新),第一次就结束了
-
从队列中抛出距离最近的那个点B(第一次就是0周围邻居)。这个点距离一定是最近的(所有权值都是正的,点的距离只能越来越长。)标记这个点为true,并且将这个点的邻居加入队列(下一次确定的最短点在前面未确定和这个点邻居中产生),并更新通过B点计算各个位置的长度,如果小于则更新! 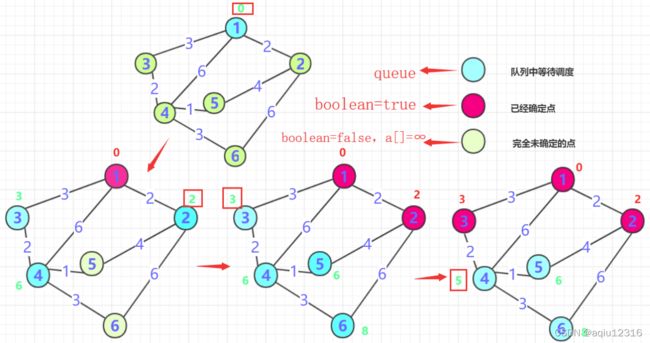
-
重复二的操作,直到所有点都确定。
-
算法实现
package 图论;
import java.util.ArrayDeque;
import java.util.Comparator;
import java.util.PriorityQueue;
import java.util.Queue;
import java.util.Scanner;
public class dijkstra {
static class node
{
int x; //节点编号
int lenth;//长度
public node(int x,int lenth) {
this.x=x;
this.lenth=lenth;
}
}
public static void main(String[] args) {
int[][] map = new int[6][6];//记录权值,顺便记录链接情况,可以考虑附加邻接表
initmap(map);//初始化
boolean bool[]=new boolean[6];//判断是否已经确定
int len[]=new int[6];//长度
for(int i=0;i<6;i++)
{
len[i]=Integer.MAX_VALUE;
}
Queueq1=new PriorityQueue(com);
len[0]=0;//从0这个点开始
q1.add(new node(0, 0));
int count=0;//计算执行了几次dijkstra
while (!q1.isEmpty()) {
node t1=q1.poll();
int index=t1.x;//节点编号
int length=t1.lenth;//节点当前点距离
bool[index]=true;//抛出的点确定
count++;//其实执行了6次就可以确定就不需要继续执行了 这句可有可无,有了减少计算次数
for(int i=0;i0&&!bool[i])
{
node node=new node(i, length+map[index][i]);
if(len[i]>node.lenth)//需要更新节点的时候更新节点并加入队列
{
len[i]=node.lenth;
q1.add(node);
}
}
}
}
for(int i=0;i<6;i++)
{
System.out.println(len[i]);
}
}
static Comparatorcom=new Comparator() {
public int compare(node o1, node o2) {
return o1.lenth-o2.lenth;
}
};
private static void initmap(int[][] map) {
map[0][1]=2;map[0][2]=3;map[0][3]=6;
map[1][0]=2;map[1][4]=4;map[1][5]=6;
map[2][0]=3;map[2][3]=2;
map[3][0]=6;map[3][2]=2;map[3][4]=1;map[3][5]=3;
map[4][1]=4;map[4][3]=1;
map[5][1]=6;map[5][3]=3;
}
}
二,贪心算法
什么是贪心算法? 贪心算法,又称贪婪算法(Greedy Algorithm),是指在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优解出发来考虑,它所做出的仅是在某种意义上的局部最优解。 贪婪算法是一种分阶段的工作,在每一个阶段,可以认为所做决定是最好的,而不考虑将来的后果。这种“眼下能够拿到的就拿”的策略是这类算法名称的来源。 贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性,即某个状态以后的过程不会影响以前的状态,只与当前状态有关。所以对所采用的贪心策略一定要仔细分析其是否满足无后效性。
贪心算法的基本思路:
-
建立数学模型来描述问题。
-
把求解的问题分成若干个子问题。
-
对每一子问题求解,得到子问题的局部最优解。
-
把子问题的解局部最优解合成原来解问题的一个解。
贪心算法适用的问题 贪心策略适用的前提是:局部最优策略能导致产生全局最优解。也就是当算法终止的时候,局部最优等于全局最优。
贪心算法的实现框架 从问题的某一初始解出发; while (能朝给定总目标前进一步) { 利用可行的决策,求出可行解的一个解元素; } 由所有解元素组合成问题的一个可行解;
贪心策略的选择 因为用贪心算法只能通过解局部最优解的策略来达到全局最优解,因此,一定要注意判断问题是否适合采用贪心算法策略,找到的解是否一定是问题的最优解。 如果确定可以使用贪心算法,那一定要选择合适的贪心策略;
1,纸币找零问题
假设1元、2元、5元、10元、20元、50元、100元的纸币,张数不限制,现在要用来支付K元,至少要多少张纸币?
很显然,我们很容易就想到使用贪心算法来解决,并且我们所根据的贪心策略是,每一步尽可能用面值大的纸币即可。当然这是正确的,代码如下:
public static void greedyGiveMoney(int money) {
System.out.println("需要找零: " + money);
int[] moneyLevel = {1, 5, 10, 20, 50, 100};
for (int i = moneyLevel.length - 1; i >= 0; i--) {
int num = money/ moneyLevel[i];
int mod = money % moneyLevel[i];
money = mod;
if (num > 0) {
System.out.println("需要" + num + "张" + moneyLevel[i] + "块的");
}
}
}
算法分析
(1)如果不限制纸币的金额,那这种情况还适合用贪心算法么。比如1元,2元,3元,4元,8元,15元的纸币,用来支付K元,至少多少张纸币?
经我们分析,这种情况是不适合用贪心算法的,因为我们上面提供的贪心策略不是最优解。比如,纸币1元,5元,6元,要支付10元的话,按照上面的算法,至少需要1张6元的,4张1元的,而实际上最优的应该是2张5元的。
(2)如果限制纸币的张数,那这种情况还适合用贪心算法么。比如1元10张,2元20张,5元1张,用来支付K元,至少多少张纸币?
同样,仔细想一下,就知道这种情况也是不适合用贪心算法的。比如1元10张,20元5张,50元1张,那用来支付60元,按照上面的算法,至少需要1张50元,10张1元,而实际上使用3张20元的即可;
(3)所以贪心算法是一种在某种范围内,局部最优的算法。
2,区域选择
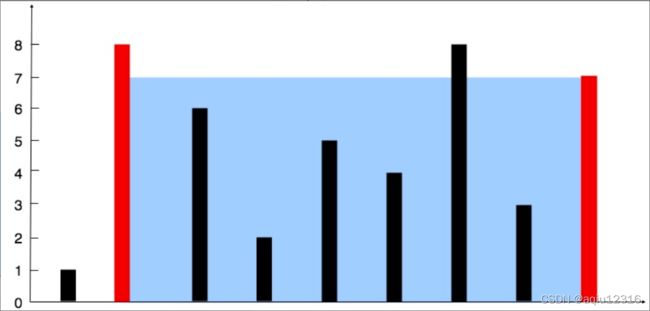
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
public static int maxArea(int[] height) {
int l=0, r=height.length-1, Max=0;
while(l
双指针+贪心 头指针表示左边界位置,尾指针表示右边界位置。每次比较左右边界高度:若左边界高度<右边界高度,最大面积=max(最大面积,左边界高度×当前宽度),左边界右移;否则最大面积=max(最大面积,右边界高度×当前宽度),右边界左移。
3,跳跃游戏
给定一个非负整数数组 nums ,你最初位于数组的 第一个下标 。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
判断你是否能够到达最后一个下标。
示例 1:
输入:nums = [2,3,1,1,4]
输出:true
解释:可以先跳 1 步,从下标 0 到达下标 1, 然后再从下标 1 跳 3 步到达最后一个下标。
示例 2:
输入:nums = [3,2,1,0,4]
输出:false
解释:无论怎样,总会到达下标为 3 的位置。但该下标的最大跳跃长度是 0 , 所以永远不可能到达最后一个下标。
public class Solution {
public boolean canJump(int[] nums) {
int n = nums.length;
int rightmost = 0;
for (int i = 0; i < n; ++i) {
if (i <= rightmost) {
rightmost = Math.max(rightmost, i + nums[i]);
if (rightmost >= n - 1) {
return true;
}
}
}
return false;
}
}
三,动态规划
基本思想:动态规划算法通常用于求解具有某种最优性质的问题。在这类问题中,可能会有许多可行解。每一个解都对应于一个值,我们希望找到具有最优解的解。动态规划算法与分治法类似,其基本思想也是将待求解问题分解成若干个子问题,先求解子问题过程中,计算当前值时往往依赖之前的求解值,然后从这些子问题的解得到原问题的解。
1,路径最大和
在下面的数字三角形中寻找一条从顶部到底边的路径,使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。只需要求出这个最大和即可,不必给出具体路径。
7
3 8
8 1 0
2 7 4 4
4 5 2 6 5
求解思路:从下向上,逆向求出每层最大值,重新计算路径最大和。
30
23 21
20 13 10
7 12 10 10
4 5 5 6 5
public static int sol(int[][] arr){
int[][] temp = new int[arr.length][arr[arr.length-1].length];
for(int i=arr.length-1;i>=0;i--){
if(i==arr.length-1){
for(int j=0;j
2,最大公共子串(LCS)
LCS(Longest Common Subsequence) 就是求两个字符串最长公共子串的问题。
比如:
String str1 = new String("21232523311324"); String str2 = new String("312123223445"); str1与str2的公共子串就是21232.
求解思路:解法就是用一个矩阵来记录两个字符串中所有位置的两个字符之间的匹配情况,若是匹配则为1,否则为0。然后求出对角线最长的1序列,其对应的位置就是最长匹配子串的位置.
但是在0和1的矩阵中找最长的1对角线序列又要花去一定的时间。通过改进矩阵的生成方式和设置标记变量,可以省去这部分时间。下面是新的矩阵生成方式:
当字符匹配的时候,我们并不是简单的给相应元素赋上1,而是赋上其左上角元素的值加一。我们用两个标记变量来标记矩阵中值最大的元素的位置,在矩阵生成的过程中来判断当前生成的元素的值是不是最大的,据此来改变标记变量的值,那么到矩阵完成的时候,最长匹配子串的位置和长度就已经出来了。
这样做速度比较快,但是花的空间太多。我们注意到在改进的矩阵生成方式当中,每生成一行,前面的那一行就已经没有用了。因此我们只需使用一维数组即可。最终的代码如下:
import java.util.ArrayList;
import java.util.List;
public class LSC {
public static List get_lsc(String str1,String str2){
int max_len = str1.length()>str2.length()?str1.length():str2.length();
int[] max = new int[max_len];
int[] index = new int[max_len];
int[] c = new int[max_len];
for(int i=0;i=0;j--){
if(str1.charAt(i)==str2.charAt(j)){
if(i==0||j==0){
c[j] = 1;
}else{
c[j] = c[j-1]+1;
}
}else{
c[j] = 0;
}
if(c[j]!=0){
if(c[j]>max[0]){
max[0] = c[j];
index[0] = j;
for(int k=1;k list = new ArrayList<>();
for(int i=0;i list = get_lsc(str1,str2);
for(String s:list){
System.out.println(s);
}
}
}
3,零钱兑换
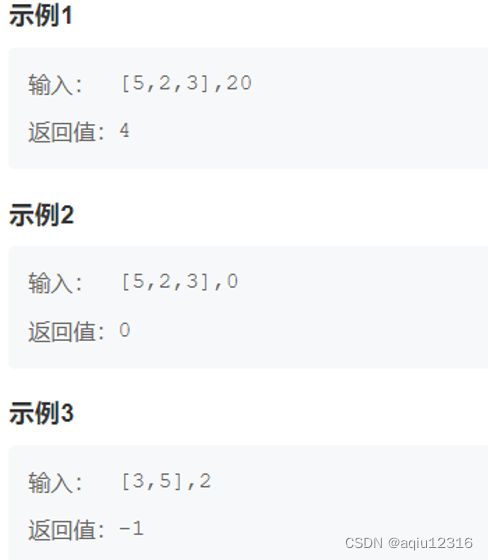
给定数组arr,arr中所有的值都为正整数且不重复。每个值代表一种面值的货币,每种面值的货币可以使用任意张,再给定一个aim,代表要找的钱数,求组成aim的最少货币数。 如果无解,请返回-1.
求解思路:使用动态规划
定义数组dp[]
dp[i] 代表给定钱数为i的时候最少货币数,即要凑成 i 元钱,至少需要dp[i] 张arr中面值纸币。
当arr[j]>i,不能兑换。
当arr[j]<=i时,dp[i]=dp[i-arr[j]]+1,即要凑成i元钱就需要凑成i-arr[j]元钱的纸币数量+1,令dp[i] = min(dp[i], dp[i-a[j]])
例如,当前纸币面额为3,即arr[j]=3,要凑成4元钱,即i=4,则凑成4元钱所需要的最少的纸币数就是dp[4],dp[4]=dp[4-3]+1,也就是说,若要凑成4元,则需要一张3元加上凑成1元的最少纸币数量。
import java.util.*;
public class Solution {
/**
* 最少货币数
* @param arr int整型一维数组 the array
* @param aim int整型 the target
* @return int整型
*/
public int minMoney (int[] arr, int aim) {
if(arr == null || arr.length == 0){
return -1;
}
int[] dp = new int[aim+1];
for(int i = 0;i<=aim;i++){
dp[i] = aim+1;
}
dp[0] = 0;
for(int i = 1;i<=aim;i++){
for(int j = 0;j< arr.length;j++){
if(arr[j] <= i){
dp[i] = Math.min(dp[i], dp[i-arr[j]] +1);
}
}
}
return (dp[aim] > aim) ?-1 : dp[aim];
}
}
4,背包问题
假设现有容量10kg的背包,另外有3个物品,分别为a1,a2,a3。物品a1重量为3kg,价值为4;物品a2重量为4kg,价值为5;物品a3重量为5kg,价值为6。将哪些物品放入背包可使得背包中的总价值最大?
求解思路:先将原始问题一般化,欲求背包能够获得的总价值,即欲求前i个物体放入容量为m(kg)背包的最大价值ci——使用一个数组来存储最大价值,当m取10,i取3时,即原始问题了。而前i个物体放入容量为m(kg)的背包,又可以转化成前(i-1)个物体放入背包的问题。下面使用数学表达式描述它们两者之间的具体关系。
public class BackPack {
public static void main(String[] args) {
int m = 10;
int n = 3;
int w[] = {3, 4, 5};
int p[] = {4, 5, 6};
int c[][] = BackPack_Solution(m, n, w, p);
for (int i = 1; i <=n; i++) {
for (int j = 1; j <=m; j++) {
System.out.print(c[i][j]+"\t");
if(j==m){
System.out.println();
}
}
}
//printPack(c, w, m, n);
}
/**
* @param m 表示背包的最大容量
* @param n 表示商品个数
* @param w 表示商品重量数组
* @param p 表示商品价值数组
*/
public static int[][] BackPack_Solution(int m, int n, int[] w, int[] p) {
//c[i][v]表示前i件物品恰放入一个重量为m的背包可以获得的最大价值
int c[][] = new int[n + 1][m + 1];
for (int i = 0; i < n + 1; i++)
c[i][0] = 0;
for (int j = 0; j < m + 1; j++)
c[0][j] = 0;
for (int i = 1; i < n + 1; i++) {
for (int j = 1; j < m + 1; j++) {
//当物品为i件重量为j时,如果第i件的重量(w[i-1])小于重量j时,c[i][j]为下列两种情况之一:
//(1)物品i不放入背包中,所以c[i][j]为c[i-1][j]的值
//(2)物品i放入背包中,则背包剩余重量为j-w[i-1],所以c[i][j]为c[i-1][j-w[i-1]]的值加上当前物品i的价值
if (w[i - 1] <= j) {
if (c[i - 1][j] < (c[i - 1][j - w[i - 1]] + p[i - 1]))
c[i][j] = c[i - 1][j - w[i - 1]] + p[i - 1];
else
c[i][j] = c[i - 1][j];
} else
c[i][j] = c[i - 1][j];
}
}
return c;
}
四,排序
1,冒泡排序
基本思想:在要排序的一组数中,对当前还未排好序的范围内的全部数,自上而下对相邻的两个数依次进行比较和调整,让较大的数往下沉,较小的往上冒。即:每当两相邻的数比较后发现它们的排序与排序要求相反时,就将它们互换。
public class bubbleSort {
public bubbleSort(){
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
int temp=0;
for(int i=0;ia[j+1]){
temp=a[j];
a[j]=a[j+1];
a[j+1]=temp;
}
}
}
for(int i=0;i
2,选择排序
基本思想:在要排序的一组数中,选出最小的一个数与第一个位置的数交换;然后在剩下的数当中再找最小的与第二个位置的数交换,如此循环到倒数第二个数和最后一个数比较为止。
publicclass selectSort {
public selectSort(){
int a[]={1,54,6,3,78,34,12,45};
int position=0;
for(int i=0;i
3,插入排序
基本思想:在要排序的一组数中,假设前面(n-1) [n>=2] 个数已经是排好顺序的,现在要把第n个数插到前面的有序数中,使得这n个数也是排好顺序的。如此反复循环,直到全部排好顺序。
package com.njue;
publicclass insertSort {
public insertSort(){
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
int temp=0;
for(int i=1;i=0&&temp
4,快速排序
基本思想:选择一个基准元素,通常选择第一个元素或者最后一个元素,通过一趟扫描,将待排序列分成两部分,一部分比基准元素小,一部分大于等于基准元素,此时基准元素在其排好序后的正确位置,然后再用同样的方法递归地排序划分的两部分。
public class quickSort {
inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
public quickSort(){
quick(a);
for(int i=0;i= tmp) {
high--;
}
list[low] = list[high]; //比中轴小的记录移到低端
while (low < high && list[low] <= tmp) {
low++;
}
list[high] = list[low]; //比中轴大的记录移到高端
}
list[low] = tmp; //中轴记录到尾
return low; //返回中轴的位置
}
public void _quickSort(int[] list, int low, int high) {
if (low < high) {
int middle = getMiddle(list, low, high); //将list数组进行一分为二
_quickSort(list, low, middle - 1); //对低字表进行递归排序
_quickSort(list, middle + 1, high); //对高字表进行递归排序
}
}
public void quick(int[] a2) {
if (a2.length > 0) { //查看数组是否为空
_quickSort(a2, 0, a2.length - 1);
}
}
}
5,归并排序
基本思想:归并(Merge)排序法是将两个(或两个以上)有序表合并成一个新的有序表,即把待排序序列分为若干个子序列,每个子序列是有序的。然后再把有序子序列合并为整体有序序列。
import java.util.Arrays;
public class mergingSort {
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
public mergingSort(){
sort(a,0,a.length-1);
for(int i=0;i
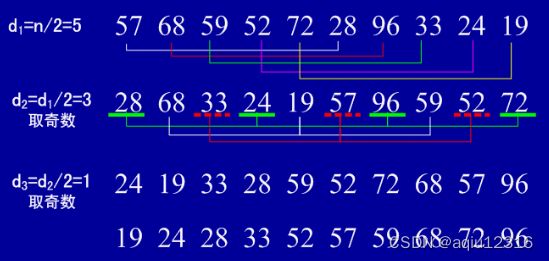
6,希尔排序
基本思想:先将要排序的一组数按某个增量d(n/2,n为要排序数的个数)分成若干组,每组中记录的下标相差d.对每组中全部元素进行直接插入排序,然后再用一个较小的增量(d/2)对它进行分组,在每组中再进行直接插入排序。当增量减到1时,进行直接插入排序后,排序完成。
publicclass shellSort {
publicshellSort(){
int a[]={1,54,6,3,78,34,12,45,56,100};
double d1=a.length;
int temp=0;
while(true){
d1= Math.ceil(d1/2);
int d=(int) d1;
for(int x=0;x=0&&temp
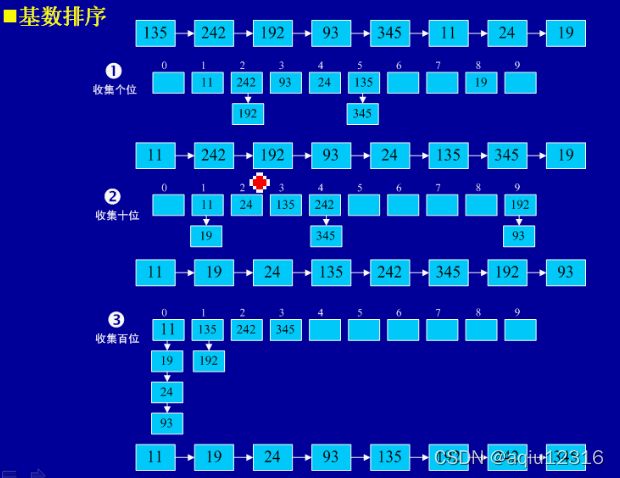
7,基数排序
基本思想:将所有待比较数值(正整数)统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序。这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
import java.util.List;
public class radixSort {
int a[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,101,56,17,18,23,34,15,35,25,53,51};
public radixSort(){
sort(a);
for(int i=0;imax){
max=array[i];
}
}
int time=0;
//判断位数;
while(max>0){
max/=10;
time++;
}
//建立10个队列;
List queue=new ArrayList();
for(int i=0;i<10;i++){
ArrayList queue1=new ArrayList();
queue.add(queue1);
}
//进行time次分配和收集;
for(int i=0;i queue2=queue.get(x);
queue2.add(array[j]);
queue.set(x, queue2);
}
int count=0;//元素计数器;
//收集队列元素;
for(int k=0;k<10;k++){
while(queue.get(k).size()>0){
ArrayList queue3=queue.get(k);
array[count]=queue3.get(0);
queue3.remove(0);
count++;
}
}
}
}
}
8,堆排序
基本思想:堆排序是一种树形选择排序,是对直接选择排序的有效改进。
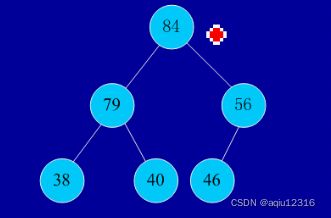
堆的定义如下:具有n个元素的序列(h1,h2,...,hn),当且仅当满足(hi>=h2i,hi>=2i+1)或(hi<=h2i,hi<=2i+1)(i=1,2,...,n/2)时称之为堆。在这里只讨论满足前者条件的堆。由堆的定义可以看出,堆顶元素(即第一个元素)必为最大项(大顶堆)。完全二叉树可以很直观地表示堆的结构。堆顶为根,其它为左子树、右子树。初始时把要排序的数的序列看作是一棵顺序存储的二叉树,调整它们的存储序,使之成为一个堆,这时堆的根节点的数最大。然后将根节点与堆的最后一个节点交换。然后对前面(n-1)个数重新调整使之成为堆。依此类推,直到只有两个节点的堆,并对它们作交换,最后得到有n个节点的有序序列。从算法描述来看,堆排序需要两个过程,一是建立堆,二是堆顶与堆的最后一个元素交换位置。所以堆排序有两个函数组成。一是建堆的渗透函数,二是反复调用渗透函数实现排序的函数。
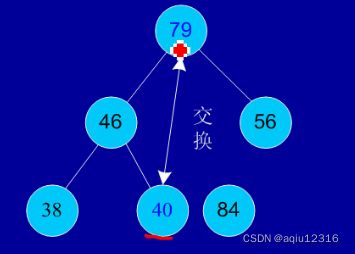
初始序列:46,79,56,38,40,84
建堆:
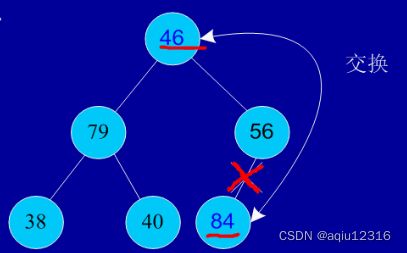
交换,从堆中踢出最大数
剩余结点再建堆,再交换踢出最大数
依次类推:最后堆中剩余的最后两个结点交换,踢出一个,排序完成。
import java.util.Arrays;
publicclass HeapSort {
inta[]={49,38,65,97,76,13,27,49,78,34,12,64,5,4,62,99,98,54,56,17,18,23,34,15,35,25,53,51};
public HeapSort(){
heapSort(a);
}
public void heapSort(int[] a){
System.out.println("开始排序");
int arrayLength=a.length;
//循环建堆
for(int i=0;i=0;i--){
//k保存正在判断的节点
int k=i;
//如果当前k节点的子节点存在
while(k*2+1<=lastIndex){
//k节点的左子节点的索引
int biggerIndex=2*k+1;
//如果biggerIndex小于lastIndex,即biggerIndex+1代表的k节点的右子节点存在
if(biggerIndex
9,计数排序
为了更好的理解计数排序,我们先来想象一下如果一个数组里所有元素都是整数,而且都在0-k以内。那对于数组里每个元素来说,如果我能知道数组里有多少项小于或等于该元素。我就能准确地给出该元素在排序后的数组的位置。
拿上图这个数组来说,元素5之前有8个元素小于等于5(含5本身),因此我排序后5所在的位置肯定是8.所以我只要构造一个(k+1)大小的数组,里面存下所有对应A中每个元素之前的元素个数,理论上就能在线性时间内完成排序。
算法过程
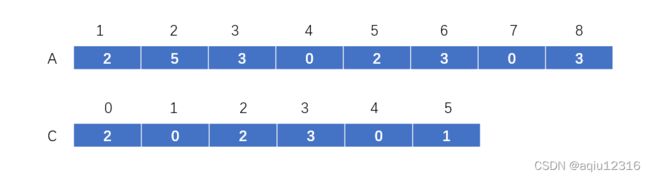
根据以上说明,我们能得出计数算法的过程:
我们可以得到原数组中有2个0,0个1,2个2,3个3,0个4,1个5.
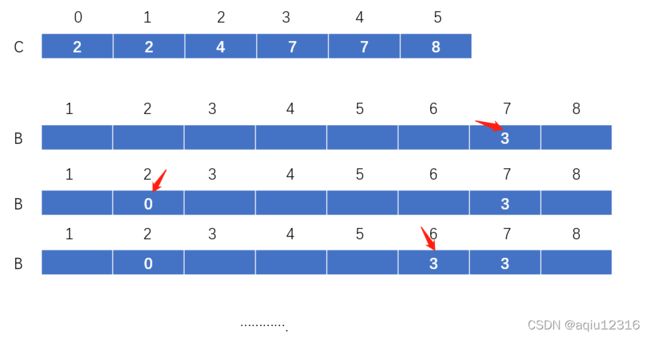
2.我们将C中每个i位置的元素大小改成C数组前i项和(基于之前的算法思考,我们不难理解这么做的道理):
3.OK,现在我们已经快看到成功的曙光了。现在要做的就是初始化一个和A同样大小的数组B用于存储排序后数组,然后倒序遍历A中元素(后面会提到为何要倒序遍历),通过查找C数组,将该元素放置到B中相应的位置,同时将C中对应的元素大小-1(表明已经放置了一个这样大小的元素,下次再放同样大小的元素,就要往前挤一个位置)。遍历完A数组后,就完成了所有的排序工作(只画出了前3步):
最后排序结果B:
我们现在回过头来思考一下为什么要限定A中是整数而且要限定元素大小?以及这个计数算法的时间复杂度是多少?
首先第一个问题,要知道我们要在C数组中存储所有A中对应元素之前的元素个数,因此如果不是整数或者大小范围无限大的话,我们就没法构造C数组,加之我们要对C数组遍历操作,如果K太大的话,这个算法的线性复杂度也就没有任何意义了。所以限制是整数纯粹只是为了限制C数组的大小,如果你想提出另外一种有限范围的限制,比如都是整数或者0.5结尾的小数(1.5,3.5等)也是可以的,只要将C的数组大小变成2k+2就可以了,只不过这种假设几乎没有任何实际意义而已。
对于第二个问题,我们来看看算法过程:第一步我们遍历了A数组,因此操作时间是Θ(n),第二步遍历C数组操作时间是Θ(k),第三步遍历A数组插入B,因此操作时间是也是Θ(n)。加起来时间复杂度就是Θ(n+k)。据此我们也能得到该算法的适用场景仅限于k较小的情况,如果k很大的话,就不如使用比较排序效率高了。
细心的读者应该还记得我在前文提过要解释为何要倒序遍历A数组,我们观察一下A数组中的3,我们可以看到有3个元素都等于3,对应位置:3,6,8。这3个3最后在5,6,7位置
我们是把8位置的3放在了7位置上,6位置的3放在了6位置上,3位置的3放在了5位置上。也就是说所有元素仍保持了之前的相对位置,我们称这个性质为排序的稳定性。有可能有人会觉得这个稳定性看起来没什么用,单纯从计数排序结果看,确实没什么用处,但是当在其他地方用到计数排序时,稳定性就非常有用了,比如前面介绍的基数排序。
package sort;
public class CountSort {
private static int[] countSort(int[] array,int k)
{
int[] C=new int[k+1];//构造C数组
int length=array.length,sum=0;//获取A数组大小用于构造B数组
int[] B=new int[length];//构造B数组
for(int i=0;i=0;i--)//遍历A数组,构造B数组
{
B[C[array[i]]-1]=array[i];//将A中该元素放到排序后数组B中指定的位置
C[array[i]]--;//将C中该元素-1,方便存放下一个同样大小的元素
}
return B;//将排序好的数组返回,完成排序
}
public static void main(String[] args)
{
int[] A=new int[]{2,5,3,0,2,3,0,3};
int[] B=countSort(A, 5);
for(int i=0;i
10,桶排序
桶排序也是时间复杂度仅为 O(n) 的一种排序方法,它假设输入数据服从均匀分布,我们将数据分别放入到 n 个桶内,先对桶内数据进行排序,然后遍历桶依次取出桶中的元素即可完成排序。
和计数排序类似,桶排序也对输入数据作了某种假设,因此它的速度也很快。具体来说,计数排序假设了输入数据都属于一个小区间内的整数,而桶排序则假设输入数据是均匀分布的,即落入每个桶中的元素数量理论也是差不多的,不会出现很多数落入同一个桶内的情况。
例如输入数据:21,8,6,11,36,50,27,42,0,12。
然后分别放入对应的桶内排序,最后依次遍历桶取出元素即可完成排序。
import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.ListIterator;
public class Main {
public static void main(String[] args) {
// 输入元素均在 [0, 10) 这个区间内
float[] arr = new float[] { 0.12f, 2.2f, 8.8f, 7.6f, 7.2f, 6.3f, 9.0f, 1.6f, 5.6f, 2.4f };
bucketSort(arr);
printArray(arr);
}
public static void bucketSort(float[] arr) {
// 新建一个桶的集合
ArrayList> buckets = new ArrayList>();
for (int i = 0; i < 10; i++) {
// 新建一个桶,并将其添加到桶的集合中去。
// 由于桶内元素会频繁的插入,所以选择 LinkedList 作为桶的数据结构
buckets.add(new LinkedList());
}
// 将输入数据全部放入桶中并完成排序
for (float data : arr) {
int index = getBucketIndex(data);
insertSort(buckets.get(index), data);
}
// 将桶中元素全部取出来并放入 arr 中输出
int index = 0;
for (LinkedList bucket : buckets) {
for (Float data : bucket) {
arr[index++] = data;
}
}
}
/**
* 计算得到输入元素应该放到哪个桶内
*/
public static int getBucketIndex(float data) {
// 这里例子写的比较简单,仅使用浮点数的整数部分作为其桶的索引值
// 实际开发中需要根据场景具体设计
return (int) data;
}
/**
* 我们选择插入排序作为桶内元素排序的方法 每当有一个新元素到来时,我们都调用该方法将其插入到恰当的位置
*/
public static void insertSort(List bucket, float data) {
ListIterator it = bucket.listIterator();
boolean insertFlag = true;
while (it.hasNext()) {
if (data <= it.next()) {
it.previous(); // 把迭代器的位置偏移回上一个位置
it.add(data); // 把数据插入到迭代器的当前位置
insertFlag = false;
break;
}
}
if (insertFlag) {
bucket.add(data); // 否则把数据插入到链表末端
}
}
public static void printArray(float[] arr) {
for (int i = 0; i < arr.length; i++) {
System.out.print(arr[i] + ", ");
}
System.out.println();
}
}
桶排序中很重要的一步就是桶的设定了,我们必须根据输入元素的情况,选择一个恰当的 “getBucketIndex” 算法,使得输入元素能够正确的放入对应的桶内,且保证输入数据能够尽量均匀的放入不同的桶内。
最糟糕的情况下,即所有的数据都放入了一个桶内,桶内自排序算法为插入排序,那么其时间复杂度就为 O(n ^ 2) 了。
其次,我们可以发现,区间划分的越细,即桶的数量越多,理论上分到每个桶中的元素就越少,桶内数据的排序就越简单,其时间复杂度就越接近于线性。
极端情况下,就是区间小到只有1,即桶内只存放一种元素,桶内的元素不再需要排序,因为它们都是相同的元素,这时桶排序差不多就和计数排序一样了。
五,查找算法
1,二分法
二分法的前提是 有序
比如 我们有一个数组{1,2,3,4,5,6,7,8.9} 我们要找 8;
有什么思路呢?for 循环 然后一个个比较?虽然说这样也行 但是当我们这个数组特别大的时候代码执行的时间就会特别长 所以就有了二分的思想
我们先拿8和我数组中间的数比较 也就是和5比较 8比5大 也就是说在整个数组中5之前都不可能有8(这也就是为什么二分法实现前提的一定是有序,如果是无序的话 我们不能保证5之前没有8) 排除了5及5之前的数 我们继续找(在{6,7,8,9}中找) {6,7,8,9}中间值7 8比7大 再继续({8,9})中找 中间值8 就找到了中间值计算方式 数组.length-1(也就是最后一个数的索引)
class BinarySearch{
/*
二分法查找
*/
public static void main(String[] args){
int[] arr = {1,2,3,4,5,6,7,8};
int a = 0;
System.out.println(binarySearch(a,arr));
}
// 二分法查找
static int binarySearch(int a,int[] arr){
// 最大索引
int maxIndex = arr.length -1;
// 最小索引
int minIndex = 0;
// 中间索引
int halfIndex = minIndex+(maxIndex-minIndex)/2;
while (minIndex<=maxIndex){
// 找到时
if (arr[halfIndex]==a){
return halfIndex;
}else if (arr[halfIndex]
二维数组的二分法其实和一维数组的差不多,就是多了个换行,多一些判断
class TwoDimensionalArray{
/*
有序的二维数组二分法
*/
public static void main(String[] args) {
int[][] arr = {{1,2,3},
{4,5,6},
{7,8,9}};
int[] res = search(arr,1);
String str = java.util.Arrays.toString(res);
System.out.println(str);
}
static int[] search(int[][] arr, int a){
int minIndex_x = 0;
int minIndex_y = 0;
int maxIndex_x = arr.length-1;
int maxIndex_y = arr[0].length-1;
int halfIndex_x = minIndex_x + (maxIndex_x - minIndex_x)/2;
int halfIndex_y = minIndex_y + (maxIndex_y - minIndex_y)/2;
int x = arr.length-1;
int y = arr[0].length-1;
while (minIndex_y <= maxIndex_y && minIndex_x <= maxIndex_x){
if (a==arr[halfIndex_x][halfIndex_y]){
int[] res = {halfIndex_x,halfIndex_y};
return res;
}else if (a>arr[halfIndex_x][halfIndex_y]){
// 搜索值比中间值大
if (halfIndex_y==y & halfIndex_x != x){
minIndex_x = halfIndex_x + 1;
minIndex_y = 0;
}else{
minIndex_y = halfIndex_y + 1;
}
}else{// 搜索值比中间值小
if (halfIndex_y==0 & halfIndex_x != 0){
maxIndex_x = halfIndex_x - 1;
maxIndex_y = y;
}else{
maxIndex_y = halfIndex_y - 1;
}
}
halfIndex_x = minIndex_x + (maxIndex_x - minIndex_x)/2;
halfIndex_y = minIndex_y + (maxIndex_y - minIndex_y)/2;
}
int[] res_null = {-1,-1};
return res_null;
}
}
2,KMP
一、什么是KMP算法?
维基百科的解释是:在计算机科学中,Knuth-Morris-Pratt字符串查找算法(简称为KMP算法)可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始,从而避免重新检查先前已经匹配过的字符。
二、字符串的前缀与后缀
前缀:字符串除了最后一个字符的全部头部组合;
后缀:字符串处理第一个字符的全部头部组合;例如
三、字符串部分匹配表
"部分匹配"的实质是,有时候,字符串头部和尾部会有重复。比如,"ABCDAB"之中有两个"AB",那么它的"部分匹配值"就是2("AB"的长度)。搜索词移动的时候,第一个"AB"向后移动4位(字符串长度-部分匹配值),就可以来到第二个"AB"的位置。所以我们需要找到一个字符串中每一个子串的匹配值,即找到字符串的部分匹配值表,这样的话我们在下面匹配字符串的过程中就可以根据匹配表来进行跳跃了,而不必一个一个字符往后移,这就是关键所在。
四、KMP算法实现过程
简单来说,KMP算法就是根据上面我们已经得到的部分匹配表来判断:匹配过程中发现子串的某个字符与待匹配串不对应时,子串应该往后移几位。
移动的位数 = 已经匹配成功的串的总长度 - 已经匹配成功的串的部分匹配值
有些绕,举个栗子,假如我要判断字符串"BBC ABCDAB ABCDABCDABDE"中是否含有串“ABCDABD”,我把前面这个长串叫做待匹配串,把“ABCDABD”叫做子串(有可能叫法不对但明白就行)。
匹配的过程为:
将字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符,进行比较。因为B与A不匹配,所以搜索词后移一位。直到有匹配的字符位置,如下:
图中当匹配到D时发现不对应了,此时:
已经匹配成功的串为:ABCDAB
已经匹配成功的串的总长度:6
已经匹配成功的串的部分匹配值 :2
移动的位数 = 6 - 2,直接将子串往后移动4位,继续开始匹配
一样的道理,此时已经匹配成功的串为AB,移动的位数 = 2 - 0,往后移动2位继续匹配
没有匹配成功的串,往后移一位
已经匹配成功的串为:ABCDAB,ABCDAB的部分匹配值为2,移动的位数 = 6 - 2,往后移动4位
此时子串所有的字符都被匹配,搜索完成。
public class KmpAlgo {
//寻找待匹配串的部分匹配值,放在next数组中
static void getNext(String pattern,int[] next){
int j = 0;
int k = -1;
next[0] = -1;
int len = pattern.length();
while(j < len-1){
if(k == -1 || pattern.charAt(j) == pattern.charAt(j)){
j++;
k++;
next[j] = k;
}else{
k = next[k];
}
}
}
static int kmp(String s,String pattern){
int i = 0;
int j = 0;
int slen = s.length();
int plen = pattern.length();
int[] next = new int[plen];
getNext(pattern,next);
while(i < slen && j < plen){
if(s.charAt(i) == pattern.charAt(j)){
i++;
j++;
}else if(next[j] == -1){
i++;
j = 0;
}else{
j = next[j];
}
if(j == plen){
return i-j;
}
}
return -1;
}
/**
*@param
*/
public static void main(String[] args){
String str = "ABCDABDEYGF";
String pat = "ABCDABD";
//KmpAlgo.kmp(str, pat);
System.out.println(KmpAlgo.kmp(str, pat));
}
}
3,哈希表查找
在记录的存储位置和它的关键字之间建立一个确定的对应关系f,使每个关键字和表中一个唯一的存储位置相对应,称这个对应关系f为哈希(散列)函数,根据这个思想建立的表称为哈希表。
在哈希表中,若出现key1≠key2,而f(key1)=f(key2),则这种现象称为地址冲突key1和key2对哈希函数f来说是同义词。根据设定的哈希函数f=H(key)和处理冲突的方法,将一组关键字映射到一个有限的连续的地址集上,并以关键字在地址集中的“象作为记录中的存储位置,这一映射过程为构造哈希表(散列表)。 好的哈希函数应该使一组关键字的哈希地址均匀分布在整个哈希表中,从而减少冲突,常用的构造哈希函数的方法有:
(1)直接地址法。取关键字或关键字的某个线性函数值为哈希地址,即H(key)=key或H(key)=a*ket+b,其中,a和b为常数 (2)数字分析法。假设关键字是r进制数(如十进制数),并且哈希表中可能出现的关键字都是事先知道的,则可选取关键字的若干数位组成哈希地址。选取的原则是使得到的哈希地址尽量避免冲突,即所选数位上的数字尽可能是随机的。 (3)平方取中法。取关键字平方后的中间几位为哈希地址。这是一种较常用的方法。通常在选定哈希函数时不一定能知道关键字的全部情况,仅取其中的几位为地址不一定合适,而一个数平方后的中间几位数和数的每一位都相关,由此得到的哈希地址随机性更大。 (4)除留余数法。取关键字被某个不大于哈希表长m的数p除后所得的余数为哈希地址。即:H(key)= key mod p(p<=m)。这是一种最简单、最常用的方法,它不仅可以键字直接取模,也可在折叠、平方取中等运算上取模。 采用均匀的哈希函数可以减少地址冲突,但是不能避免冲突,因此,必须有良好的法来处理冲突,通常,处理地址冲突的方法有以下两种:
(1)开放地址法。在开放地址法中,以发生冲突的哈希地址为自变量,通过某周哈希冲突函数得到一个新的空闲的哈希地址。这种得到新地址的方法有很多种,主要有线性探查法和平方探查法。线性探查法是从发生冲突的地址开始,依次探查该地址的下一地址,直到找到一个空闲单元为止。而平方探查法则是在发生冲突的地址上加减某个因子的平方作为新的地址。 (2)拉链法。拉链法是把所有的同义词用单链表链接起来的方法。在这种方哈希表中每个单元中存放的不再是记录本身,而是相应同义词单链表的头指针。 例1:有如下数字构成的序列:A = { 7,4,1,14,100,30,5,9,20,134 } 请构造一张哈希表。 对数字序列:A = { 7,4,1,14,100,30,5,9,20,134 }中的10个元素,就可以采用除留余数法来构造哈希表,哈希函数为H(key)=key%p(p<=m),其中p用13,m用15,而对与哈希冲突的解决,可以采用开放地址中的线性探查法,具体构造哈希表的过程如下:
首先在哈希表可用空间里取用15个连续空间来存放对应元素,对于A中第一个元素用哈希函数求其对应的空间位置为:7%13=7,所以把第一个元素7放入位置为7的空间里。
对于A中第二个元素4,用哈希函数求其对应的空间位置为:4%13=4,所以把第个元素4放入位置为4的空间里。
对于A中第三个元素1,用哈希函数求其对应的空间位置为:1%13=1,所以把第三个元素1放入位置为1的空间里。
对于A中第四个元素14,用哈徐函数求其对应的空间地址为:14%13=1,但由于位置1的空间里有元素了,就采用开发地址中的线性探查法解决地址冲突,依此往后探索地址,得到位置2的空间可用,所以把第4个元素14放入位置2的空间里。
按如此寻址规律循环下去,把剩下的元素全部放入哈希表中,得到哈希表如下:
为了便于查验构造哈希表结果的正确性,构造哈希表的代码里面添加了显示哈希表内容的函数和构造哈希表驱动程序,具体代码如下:
public class HashTable {
public int[] key;
public int nullKey = -1;
public int count = 0;
public HashTable() {
this.key = new int[50];
}
public void insertHT(HashTable ha, int key, int p, int m) {
int i, adr;
adr = key % p;
if (ha.key[adr] == nullKey){
ha.key[adr] = key;
ha.count = 1;
} else {
i = 1;
do {
adr = (adr + 1) % m;
} while (ha.key[adr] != nullKey);
ha.key[adr] = key;
ha.count = i;
}
}
public void createHT(HashTable ha, int [] a, int n, int m, int p) {
int i;
for (i = 0; i < m; i++){
ha.key[i] = nullKey;
ha.count = 0;
}
for (i = 0; i < n; i++) {
insertHT(ha, a[i], p, m);
}
}
public void dispHT(HashTable ha, int m){
int i;
for (i = 0; i < m; i++) {
System.out.println(i + " ");
}
System.out.println();
for (i = 0; i < m; i++) {
if (ha.key[i] != nullKey) {
if (ha.key[i] < 10) {
System.out.println(ha.key[i] + " ");
} else if (ha.key[i] >= 100) {
System.out.println(ha.key[i] + " ");
} else {
System.out.println(ha.key[i] + " ");
}
} else {
System.out.println(" ");
}
}
System.out.println();
}
public static void main(String[] args) {
int[] a= {7, 4, 1, 14, 100, 30, 5, 9, 20, 134};
HashTable ht = new HashTable();
ht.createHT(ht, a, a.length, 15, 13);
ht.dispHT(ht, 15);
}
}
例2:在例:1所构造的哈希表中,查找100是否存在,并输出结果。 在哈希表中对X值(如100)进行查找,则按照哈希函数获取待查元素的地址,若对应地址空间的值不等于待查元素的值,则线性搜索下一地址,比较对应地址空间的值,直到找到为止;若搜索到哈希表尾都未找到,则查找失败,具体Java代码如下:
public int searchHT(HashTable ha, int p, int m, int a){
int adr;
adr = a % p;
while (ha.key[adr]!=nullKey && ha.key[adr]!=a) {
adr=(adr+1)%m;
}
if (ha.key[adr]==a) {
return adr;
} else {
return -1;
}
}
public static void main(String[] args) {
int[] a= {7, 4, 1, 14, 100, 30, 5, 9, 20, 134};
HashTable ht = new HashTable();
ht.createHT(ht, a, a.length, 15, 13);
ht.dispHT(ht, 15);
int x = ht.searchHT(ht, 13, 15, 100);
if (x==-1) {
System.out.println("查找失败,不存在该元素");
} else {
}
System.out.println("查找成功,该元素的地址为:" + x);
}
算法分析:哈希表查找法查找成功时的平均查找长度是指查到表中已有的表象的平均获查次数,它是找到表中各个已有表项的探查次数的平均值。而查找不成功的平均查装长度是指在表中查找不到待查的表项,但找到插入位置的平均探查次数,它是表中所有可能散列到的位置上要插入新元素时未找到空位置的探查次数的平均值。
4,字典树(Tire-Tree)查找
字典树又称单词查找树,Trie树,是一种树形结构,是一种哈希树的变种。典型应用是用于统计,排序和保存大量的字符串(但不仅限于字符串),所以经常被搜索引擎系统用于文本词频统计。它的优点是:利用字符串的公共前缀来节约存储空间,最大限度地减少无谓的字符串比较,查询效率比哈希表高。
Trie的核心思想是空间换时间。利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。 3个基本性质: 1.根节点不包含字符,除根节点外每一个节点都只包含一个字符。 2.从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。 3.每个节点的所有子节点包含的字符都不相同。
Trie树的构建 本质上,Trie是一颗存储多个字符串的树。相邻节点间的边代表一个字符,这样树的每条分支代表一则子串,而树的叶节点则代表完整的字符串。和普通树不同的地方是,相同的字符串前缀共享同一条分支。举一个例子。给出一组单词,inn, int, at, age, adv, ant, 我们可以得到下面的Trie: 搭建Trie的基本算法很简单,无非是逐一把每则单词的每个字母插入Trie。插入前先看前缀是否存在。如果存在,就共享,否则创建对应的节点和边。比如要插入单词add,就有下面几步: 1. 考察前缀"a",发现边a已经存在。于是顺着边a走到节点a。 2. 考察剩下的字符串"dd"的前缀"d",发现从节点a出发,已经有边d存在。于是顺着边d走到节点ad 3. 考察最后一个字符"d",这下从节点ad出发没有边d了,于是创建节点ad的子节点add,并把边ad->add标记为d。
字典树与字典很相似,当你要查一个单词是不是在字典树中,首先看单词的第一个字母是不是在字典的第一层,如果不在,说明字典树里没有该单词,如果在就在该字母的孩子节点里找是不是有单词的第二个字母,没有说明没有该单词,有的话用同样的方法继续查找.字典树不仅可以用来储存字母,也可以储存数字等其它数据。
普通数组LIST查找字符串和字典树查找字符串比较
import java.io.*;
import java.util.*;
//测试字典树的建立以及测试
public class testtrie {
public static void main(String[] args) {
// TODO 自动生成的方法存根
testbasic();
tree root=null;
root=createtree(root);
long startTime = System.currentTimeMillis();//获取当前时间
teststr(root);
long endTime = System.currentTimeMillis();
System.out.println("字典树查询字符串程序运行时间:"+(endTime-startTime)+"ms");
}
//普通数组测试查找字符串
public static void testbasic(){
try {
List strlist=new ArrayList();
File file=new File("E:\\strs.txt");
if(file.isFile() && file.exists()){ //判断文件是否存在
InputStreamReader read = new InputStreamReader(
new FileInputStream(file));//考虑到编码格式
BufferedReader bufferedReader = new BufferedReader(read);
String lineTxt = null;
while((lineTxt = bufferedReader.readLine()) != null){
strlist.add(lineTxt);
}
read.close();
long startTime = System.currentTimeMillis();//获取当前时间
try {
file=new File("E:\\strs.txt");
if(file.isFile() && file.exists()){ //判断文件是否存在
read = new InputStreamReader(
new FileInputStream(file));//考虑到编码格式
bufferedReader = new BufferedReader(read);
lineTxt = null;
while((lineTxt = bufferedReader.readLine()) != null){
if(!strlist.contains(lineTxt)){
System.out.println("NO");
}
}
read.close();
}else{
System.out.println("找不到指定的文件");
}
} catch (Exception e) {
System.out.println("读取文件内容出错");
e.printStackTrace();
}
long endTime = System.currentTimeMillis();
System.out.println("普通查询字符串程序运行时间:"+(endTime-startTime)+"ms");
}else{
System.out.println("找不到指定的文件");
}
} catch (Exception e) {
System.out.println("读取文件内容出错");
e.printStackTrace();
}
}
//字典树方法测试查找字符串
public static void teststr(tree root){
try {
File file=new File("E:\\strs.txt");
if(file.isFile() && file.exists()){ //判断文件是否存在
InputStreamReader read = new InputStreamReader(
new FileInputStream(file));//考虑到编码格式
BufferedReader bufferedReader = new BufferedReader(read);
String lineTxt = null;
while((lineTxt = bufferedReader.readLine()) != null){
if(!Search_intree(root,lineTxt)){
System.out.println("NO");
}
}
read.close();
}else{
System.out.println("找不到指定的文件");
}
} catch (Exception e) {
System.out.println("读取文件内容出错");
e.printStackTrace();
}
}
public static tree createtree(tree root){
root=new tree('#');
try {
File file=new File("E:\\strs.txt");
if(file.isFile() && file.exists()){ //判断文件是否存在
InputStreamReader read = new InputStreamReader(
new FileInputStream(file));//考虑到编码格式
BufferedReader bufferedReader = new BufferedReader(read);
String lineTxt = null;
while((lineTxt = bufferedReader.readLine()) != null){
insertintotree(root,lineTxt);//建立该字符串的字典树
}
read.close();
}else{
System.out.println("找不到指定的文件");
}
} catch (Exception e) {
System.out.println("读取文件内容出错");
e.printStackTrace();
}
System.out.println("创建字典树完成!");
return root;
}
public static void insertintotree(tree root,String str){
if(root==null || str.length()==0){
return ;
}
for(int i=0;i='a' && str.charAt(i)<='z'){
if(root.childs[str.charAt(i)-'a']==null){
tree node=new tree(str.charAt(i));
root.childs[str.charAt(i)-'a']=node;
root.childcount++;
root=node;
}else{
root=root.childs[str.charAt(i)-'a'];
}
}
}
root.flag=true;
}
public static void PreOrder(tree root){
if(root!=null){
System.out.print(root.data);
if(root.childcount!=0){
for(int i=0;i<26;i++){
PreOrder(root.childs[i]);
}
}else{
System.out.println();
}
}
}
public static boolean Search_intree(tree root,String str){
if(root==null || str.length()==0){
return false;
}else{
int i=0;
for(i=0;i
六,复杂度计算
不同时间复杂度时间变化图
2,空间复杂度