数据结构-栈

数据结构-栈

---

---

前言

栈作为一种基本的数据结构，属于线性序列结构，典型的特点是先进后出(先出后进)。在实际应用中有很多例子，例如：网络浏览器多会将用户最近访问过的地址组织为一个栈。这样，用户每访问一个新页面，其地址就会被存放至栈顶；而用户每按下一次“后退”按钮，即可沿相反的次序返回此前刚访问过的页面。类似地，主流的文本编辑器也大都支持编辑操作的历史记录功能，用户的编辑操作被依次记录在一个栈中。一旦出现误操作，用户只需按下“撤销”按钮，即可取消最近一次操作并回到此前的编辑状态。

---

一、栈是什么？

• 1.栈的介绍：

  栈(Stack)是存放数据的一种特殊线性容器，其中的数据元素按线性的逻辑次序排列。与线性向量容器不同之处在于，其仅支持在容器的某一特定端进行插入和删除操作。其中，栈中可操作的一段称为栈顶(stack top)，另一端无法直接操作的称之为栈底(stack bottom)。

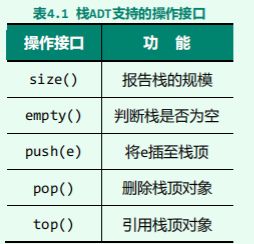
• 2.栈支持的操作接口：

  
  其中，插入(push)操作称为入栈，删除(pop)操作称出栈。

• 3.栈的特点：

• 栈中元素接受操作的次序必然始终遵循所谓后进先出（last-in-first-out, LIFO）的规律：从栈结构的整个生命期来看，更晚（早） 出栈的元素，应为更早（晚）入栈者；反之，更晚（早）入栈者应更早（晚）出栈。

• 4.栈的操作示例：

二、栈的实现

1.栈(Stack)-头文件

#ifndef STACK_STACK_H
#define STACK_STACK_H

#include 

const int DEFAULT_CAPACITY = 3; //默认容量

template<typename T> class Stack {

public:
    explicit Stack(int capacity=DEFAULT_CAPACITY);
    ~Stack();

public:
    bool empty() const;  //判断栈是否为空
    int size() const;    //获取栈的大小
    T pop();   //出栈
    void push(T const& e); //出栈
    T& top();  //取栈顶元素
private:
    int _size;  //栈的大小
    int _capacity; //容量
    T* _elem;  //栈中的元素
};
#endif //STACK_STACK_H

2.栈-cpp文件

//构造函数
template<typename T>
Stack<T>::Stack(int capacity):_size(0),_capacity(capacity){
    _elem = new T[_capacity];
}

//析构函数
template<typename T>
Stack<T>::~Stack() {
    delete[] _elem;
}

//入栈
template<typename T>
void Stack<T>::push(const T &e) {
    //判断是否需要扩容
    if(_size>=_capacity) {
        T* _oldElem = _elem;
        //容器容量扩大为原来的两倍
        _elem = new T[_capacity<<=1];
        for(int i=0;i<_size;i++) {
            _elem[i] = _oldElem[i];
        }
        delete[] _oldElem;
    }
    //入栈
    _elem[_size] = e;
    _size++;
}

//判栈是否为空
template<typename T>
bool Stack<T>::empty() const {
    return !_size;
}

//判断栈的大小
template<typename T>
int Stack<T>::size() const {
    return _size;
}

//出栈
template<typename T>
T Stack<T>::pop() {
    if(empty()) {
        std::cout<<"stack is empty,operator 'pop' error";
        std::cout<<std::endl;
        return 0;
    }
    T e = _elem[_size-1];
    _size--;
    //如果必要对容器容量进行收缩
    if(_capacity<DEFAULT_CAPACITY<<1) {
        return e;
    }
    //收缩的下界为容器容量的25%
    if(_size<<2 > _capacity) {
        return e;
    }
    T* oldElem = _elem;
    _elem = new T[_capacity>>=1];
    for(int i=0; i<_size; i++) {
        _elem[i] = oldElem[i];
    }
    delete[] oldElem;
    return e;
}

//获取栈顶元素
template<typename T>
T &Stack<T>::top() {
    return _elem[_size-1];
}

---

栈的典型应用

1. 逆序输出

在栈所擅长解决的典型问题中，有一类具有以下共同特征：首先，虽有明确的算法，但其解
答却以线性序列的形式给出；其次，无论是递归还是迭代实现，该序列都是依逆序计算输出的；
最后，输入和输出规模不确定，难以事先确定盛放输出数据的容器大小。因其特有的“后进先出”
特性及其在容量方面的自适应性，使用栈来解决此类问题可谓恰到好处。
例：进制转换：

#include "Stack.h"

/****************************
 * 十进制向其他进制进行转换
 * @param s：char类型栈，存储转换后数据
 * @param n：需转换的十进制数据
 * @param base: 转换目标进制
 *****************************/
void convert(Stack<char>& s, __int64 n, int base) {
    static char digit[] = {'0','1','2','3','4','5','6','7','8','9','A','B','C','D','E','F'};
    while(n > 0) {
        int reminder = (int)(n%base);
        s.push(digit[reminder]);
        n /= base;
    }
}


//数据测试
int main() {
    Stack<char> s;
    convert(s,1024,2);
    while(!s.empty()) {
        printf("%c",s.pop());
    }
    return 0;
}

---

2. 递归嵌套:

具有自相似性的问题多可嵌套地递归描述，但因分支位置和嵌套深度并不固定，其递归算法
的复杂度不易控制。栈结构及其操作天然地具有递归嵌套性，故可用以高效地解决这类问题。
例1：括号匹配：

#ifndef STACK_PAREN_H
#define STACK_PAREN_H

#include "Stack.h"

/***********************
 * 检查括号匹配
 * @param exp 待检查括号匹配表达式
 * @param lo 表达式待检查匹配区间下限
 * @param hi 表达式待检查匹配区间上限
 * @return 括号匹配返回True,否则返回false
**************************/
bool paren(const char exp[], int lo, int hi) {
    Stack<char> s;
    for (int i = lo; i < hi; i++) {
        //如遇见左括号入栈
        if(exp[i]=='('||exp[i]=='{'||exp[i]=='[') {
            s.push(exp[i]);
        } else if(!s.empty()) {
            //遇到右括号，栈弹出左括号进行匹配，
            //若不匹配则返回false
            if(exp[i]==')'&&s.pop()!='(') {
                return false;
            }
            if(exp[i]=='}'&&s.pop()!='{') {
                return false;
            }
            if(exp[i]==']'&&s.pop()!='[') {
                return false;
            }
        } else {
            //遇到右括号，且栈为空，则括号必不匹配
            return false;
        }
    }
    //栈为空，表示括号匹配，否则不匹配；
    return s.empty();
}

#endif //STACK_PAREN_H

例2：鉴别栈混淆：

#ifndef STACK_STACKPERMUTATION_H
#define STACK_STACKPERMUTATION_H
#include "Stack.h"
/***********************
 * 鉴别栈混淆
 * @param source 源栈排列
 * @param target 待检查目标栈
 * @return 若是栈混淆返回true,否则返回false
 */
bool isStackPermutation(Stack<char> source, const char target[]) {
    Stack<char> s;
    int num = source.size();
    for(int i=0;i<num;i++) {
        s.push(source.pop());
        if(s.top()==target[i]) {
            s.pop();
        }
        if(source.empty()&&!s.empty()) {
            return false;
        }
    }
    return true;
}

#endif //STACK_STACKPERMUTATION_H

---

3.延迟缓冲:

在一些应用问题中，输入可分解为多个单元并通过迭代依次扫描处理，但过程中的各步计算
往往滞后于扫描的进度，需要待到必要的信息已完整到一定程度之后，才能作出判断并实施计算。
在这类场合，栈结构则可以扮演数据缓冲区的角色。