《动手学深度学习 Pytorch版》 7.3 网络中的网络(NiN)

LeNet、AlexNet和VGG的设计模式都是先用卷积层与汇聚层提取特征，然后用全连接层对特征进行处理。

AlexNet和VGG对LeNet的改进主要在于扩大和加深这两个模块。网络中的网络（NiN）则是在每个像素的通道上分别使用多层感知机。

import torch
from torch import nn
from d2l import torch as d2l

7.3.1 NiN

NiN的想法是在每个像素位置应用一个全连接层。 如果我们将权重连接到每个空间位置，我们可以将其视为 $1\times 1$ 卷积层，即是作为在每个像素位置上独立作用的全连接层。 从另一个角度看，是将空间维度中的每个像素视为单个样本，将通道维度视为不同特征（feature）。

NiN块以一个普通卷积层开始，后面是两个 $1\times 1$ 的卷积层。这两个卷积层充当带有ReLU激活函数的逐像素全连接层。

def nin_block(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

7.3.2 NiN 模型

最初的 NiN 网络是在 AlexNet 后不久提出的，显然 NiN 网络是从 AlexNet 中得到了一些启示的。 NiN 使用窗口形状为 $11\times 11$ 、 $5\times 5$ 和 $3\times 3$ 的卷积层，输出通道数量与 AlexNet 中的相同。每个NiN块后有一个最大汇聚层，汇聚窗口形状为 $3\times 3$ ，步幅为 2。

NiN 和 AlexNet 之间的显著区别是 NiN 使用一个 NiN 块取代了全连接层。其输出通道数等于标签类别的数量。最后放一个全局平均汇聚层，生成一个对数几率。

NiN 设计的一个优点是显著减少了模型所需参数的数量。然而，在实践中，这种设计有时会增加训练模型的时间。

net = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

X = torch.rand(size=(1, 1, 224, 224))
for layer in net:
    X = layer(X)
    print(layer.__class__.__name__,'output shape:\t', X.shape)

Sequential output shape:	 torch.Size([1, 96, 54, 54])
MaxPool2d output shape:	 torch.Size([1, 96, 26, 26])
Sequential output shape:	 torch.Size([1, 256, 26, 26])
MaxPool2d output shape:	 torch.Size([1, 256, 12, 12])
Sequential output shape:	 torch.Size([1, 384, 12, 12])
MaxPool2d output shape:	 torch.Size([1, 384, 5, 5])
Dropout output shape:	 torch.Size([1, 384, 5, 5])
Sequential output shape:	 torch.Size([1, 10, 5, 5])
AdaptiveAvgPool2d output shape:	 torch.Size([1, 10, 1, 1])
Flatten output shape:	 torch.Size([1, 10])

7.3.3 训练模型

lr, num_epochs, batch_size = 0.1, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
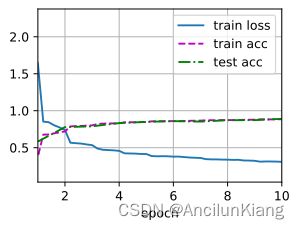
d2l.train_ch6(net, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())  # 大约需要二十五分钟，慎跑

loss 0.600, train acc 0.769, test acc 0.775
447.9 examples/sec on cuda:0

练习

（1）调整 NiN 的超参数，以提高分类准确性。

net2 = nn.Sequential(
    nin_block(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    nin_block(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    nn.Flatten())

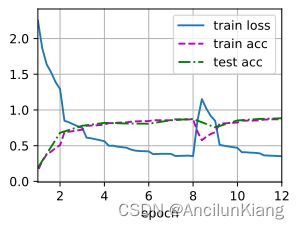
lr, num_epochs, batch_size = 0.15, 12, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net2, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())  # 大约需要三十分钟，慎跑

loss 0.353, train acc 0.871, test acc 0.884
449.5 examples/sec on cuda:0

学习率调大一点点之后精度更高了，但是波动变的分外严重。

---

（2）为什么 NiN 块中有两个 $1\times 1$ 的卷积层？删除其中一个，然后观察和分析实验现象。

def nin_block2(in_channels, out_channels, kernel_size, strides, padding):
    return nn.Sequential(
        nn.Conv2d(in_channels, out_channels, kernel_size, strides, padding),
        nn.ReLU(),
        nn.Conv2d(out_channels, out_channels, kernel_size=1), nn.ReLU())

net3 = nn.Sequential(
    nin_block2(1, 96, kernel_size=11, strides=4, padding=0),
    nn.MaxPool2d(3, stride=2),
    nin_block2(96, 256, kernel_size=5, strides=1, padding=2),
    nn.MaxPool2d(3, stride=2),
    nin_block2(256, 384, kernel_size=3, strides=1, padding=1),
    nn.MaxPool2d(3, stride=2),
    nn.Dropout(0.5),
    # 标签类别数是10
    nin_block2(384, 10, kernel_size=3, strides=1, padding=1),
    nn.AdaptiveAvgPool2d((1, 1)),
    # 将四维的输出转成二维的输出，其形状为(批量大小,10)
    nn.Flatten())

lr, num_epochs, batch_size = 0.15, 10, 128
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size, resize=224)
d2l.train_ch6(net3, train_iter, test_iter, num_epochs, lr, d2l.try_gpu())  # 大约需要二十分钟，慎跑

loss 0.309, train acc 0.884, test acc 0.890
607.5 examples/sec on cuda:0

有时候会更好，有时候会不收敛。

---

（3）计算 NiN 的资源使用情况。

a. 参数的数量是多少？

b. 计算量是多少？

c. 训练期间需要多少显存?

d. 预测期间需要多少显存?

a. 参数数量：

$$\begin{array}{rl}& [11\times 11+2]+[5\times 5+2]+[3\times 3+2]+[3\times 3+2]\\ =& 123+27+11+11\\ =& 172\end{array}$$

b. 计算量：

$$\begin{array}{rl}& \{[(224-11+4)/4{]}^2\times 11^2\times 96+224^2\times 2\}+[(26-5+2+1{)}^2\times 5^2\times 96\times 256+26^2\times 2]+\\ & [(12-3+1+1{)}^2\times 3^2\times 256\times 384+12^2\times 2]+[(5-3+1+1{)}^2\times 3^2\times 384\times 10+5^2\times 2]\\ =& 34286966+353895752+107053344+553010\\ =& 495789072\end{array}$$

---

（4）一次性直接将 $384\times 5\times 5$ 的表示压缩为 $10\times 5\times 5$ 的表示，会存在哪些问题？

压缩太快可能导致特征损失过多。