刷题学习—算法思想(双指针、排序、回溯、二分法、滑动窗口、贪心、单调栈)
算法思想
第一章 算法性能分析
1.时间复杂度分析
- 时间复杂度是一个函数,它定性描述该算法的运行时间。
- 大O用来表示上界的,当用它作为算法的最坏情况运行时间的上界,就是对任意数据输入的运行时间的上界
- 输入数据的形式对程序运算时间是有很大影响的,在数据本来有序的情况下时间复杂度是O(n),但如果数据是逆序的话,插入排序的时间复杂度就是O(n^2)。也就有了最坏时间复杂度的概念,如果输入的数据是逆序,自然排序的时间就会长。就要时刻想着数据用例的不一样,时间复杂度也是不同的
- 在决定使用哪些算法的时候,不是时间复杂越低的越好(因为简化后的时间复杂度忽略了常数项等等),要考虑数据规模,如果数据规模很小甚至可以用O(n^2)的算法比O(n)的更合适
- 时间复杂度都是省略常数项系数的,是因为一般情况下都是默认数据规模足够的大,基于这样的事实,给出的算法时间复杂的的一个排行:O(1)常数阶 < O(logn)对数阶 < O(n)线性阶 < O(n^2)平方阶 < O(n^3)(立方阶) < O(2^n) (指数阶)
- O(logn)中的log:抽出来以2为底的10是常数,所以还是一律叫做logn
2.空间复杂度分析
- 空间复杂度是对一个算法在运行过程中占用内存空间大小的量度,记做S(n)=O(f(n)。可以对程序运行中需要多少内存有个预先估计。
- 求其空间复杂度公式:递归算法的空间复杂度 = 每次递归的空间复杂度 * 递归深度
第二章 双指针
1. 两数之和 II - 输入有序数组
找到数组中两数和为目标值的数,返回计数位置
双指针单向双层逐个遍历:182ms
class Solution {
public int[] twoSum(int[] numbers, int target) {
for (int i = 0; i < numbers.length; i++) {
for (int j = i + 1; j < numbers.length; j++) {
if(target == numbers[i] + numbers[j])return new int[]{
i + 1,j + 1};
}
}
return null;
}
}
双指针法不讨论
运用hash表:2ms
class Solution {
public int[] twoSum(int[] numbers, int target) {
HashMap<Integer, Integer> map = new HashMap<>();
int[] arr = new int[2];
for (int i = 0; i < numbers.length; i++) {
if(map.containsKey(target - numbers[i])){
return new int[]{
map.get(target - numbers[i]) + 1,i + 1};
}
map.put(numbers[i],i);
}
return null;
}
}
双指针单层双向遍历:0ms
class Solution {
public int[] twoSum(int[] numbers, int target) {
if(numbers == null)return null;
int i = 0,j = numbers.length - 1;
while (i < j) {
int sum = numbers[i] + numbers[j];
if(sum > target){
j--;
} else if (sum < target) {
i++;
}else {
return new int[]{
i + 1,j + 1};
}
}
return null;
}
}
- 双指针单向双层逐个遍历:对数组中所有的两个数进行了遍历,时间复杂度为O ( n ^ 2)
- hash表:遍历一次,所以时间复杂度为O ( n ),空间复杂度也为O ( n )
- 双指针单层双向遍历:双向遍历,时间复杂度为O ( n ),空间复杂度为O ( 1 )
★总结:
- 双指针法不一定采用双层单向遍历,如果仅限于 双指针单向双层逐个遍历,几乎是暴力解法。双指针是一个很好的算法思路,用双指针解可以考虑第三种单层双向遍历,效率要高的多
- 对于逻辑简单,题目不复杂的题,需要寻找两个数的时候,可以采用双指针
2.平方数之和
是否存在一个数,是两个数的平方的和
运用sqrt函数,即取根,为了方式数据溢出,取一个数的平方要定义成long型
class Solution {
public boolean judgeSquareSum(int c) {
for (long a = 0; a * a <= c; a++) {
double b = Math.sqrt(c - a * a);
if(b == (int) b){
return true;
}
}
return false;
}
}
双指针双向减小范围验证是否是平方和数
class Solution {
public boolean judgeSquareSum(int c) {
long a = 0;
long b = (long) Math.sqrt(c - a * a);
while (a <= b) {
long sum = a * a + b * b;
if (sum > (long) c) {
b--;
}else if(sum < (long) c){
a++;
}else {
return true;
}
}
return false;
}
}
先假设两个数,一大一小,计算它们的平方和数
不断减小区间至两数相等,如果存在他们的和等于形参,说明是对的
3.反转字符串中的元音字母
class Solution {
public String reverseVowels(String s) {
if(s == null)return null;
char[] carr = s.toCharArray();
long a = 0;
long b = carr.length - 1;
while (a < b) {
if(isYuan(carr[(int) b]) && isYuan(carr[(int) a])){
char tmp = carr[(int) b];
carr[(int) b] = carr[(int) a];
carr[(int) a] = tmp;
a++;
b--;
}else if(isYuan(carr[(int) a]) && !isYuan(carr[(int) b])){
b--;
}else if(!isYuan(carr[(int) a]) && isYuan(carr[(int) b])){
a++;
}else {
a++;
b--;
}
}
return new String(carr);
}
public boolean isYuan(char c){
if(c == 'a' || c == 'e' || c == 'i' || c == 'o' || c == 'u' ||
c == 'A' || c == 'E' || c == 'I' || c == 'O' || c == 'U')return true;
return false;
}
}
思路:
- 定义一个方法,判断是否是元音字母
- 将字符串转为char数组,双指针分头遍历,只有双指针均指向元音字母时,进行调换
- 调换成功后返回新的字符串
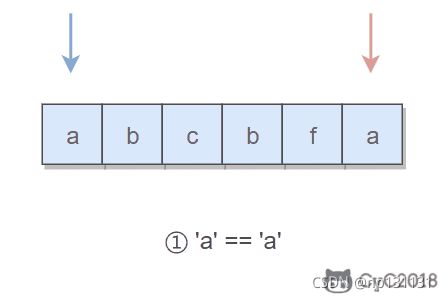
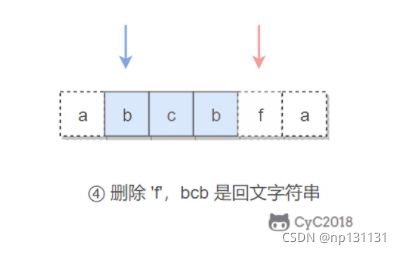
4.验证回文字符串 Ⅱ
给定一个非空字符串 s,最多删除一个字符。判断是否能成为回文字符串。
可以删除一个字符,判断是否能构成回文字符串。
class Solution {
public boolean validPalindrome(String s) {
for (int i = 0,j = s.length() - 1; i < j; i++,j--) {
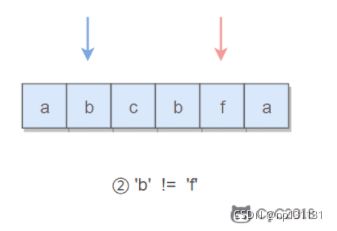
if(s.charAt(i) != s.charAt(j)){
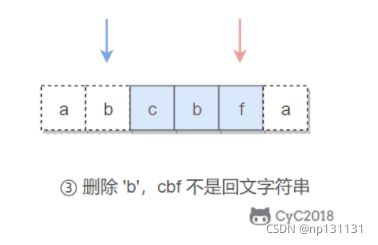
//当前不等没关系但是后面要是有一个是回文串,就说明符合题意,如abac
return isvalidPalindrome(s,i,j - 1) || isvalidPalindrome(s,i + 1,j);
}
}
return true;//对应的字符都相等了,出来的就是回文串
}
public boolean isvalidPalindrome(String s,int b,int e){
while (b < e) {
if (s.charAt(b++) != s.charAt(e--)) {
return false;
}
}
return true;
}
}
- 先构造一个判断回文数的方法,给予前后索引指针来判断
- 双指针双向遍历,只要当前双指针指向的字符不相等,就保留一个索引移动另一个索引(达到删除一个字符的目的)
- 因为之前对应的字符已经是对称的了,所以他们的子串如果有一个是回文的,说明删除一个字符后存在有回文串,那么就能计算出答案
5.合并两个有序数组
①合并后排序但是面试时属于最差解法
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
for (int i = m,j = 0; i < nums1.length && j < nums2.length; i++,j++) {
nums1[i] = nums2[j];
}
Arrays.sort(nums1);
}
}
②常规双指针
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int[] arr = new int[m + n];
int i1 = 0,i2 = 0;
int cur;
while (i1 < m || i2 < n) {
if(i1 == m){
//索引到达数组1的尾部
cur = nums2[i2++];
}else if(i2 == n){
//索引到达数组2的尾部
cur = nums1[i1++];
}else if(nums1[i1] < nums2[i2]){
cur = nums1[i1++];
}else {
cur = nums2[i2++];
}
arr[i1 + i2 - 1] = cur;
}
for (int i = 0; i < m + n; i++) {
nums1[i] = arr[i];
}
}
}
思路:
- 构建一个新数组,对两个数组开头定一个索引,逐个合并放入新数组
- 再将新数组转到nums1中
★③逆序双指针:
class Solution {
public void merge(int[] nums1, int m, int[] nums2, int n) {
int tail = nums1.length - 1;//尾索引
int i1 = m - 1;
int i2 = n - 1;
while (i2 >= 0) {
if(i1 < 0 || nums1[i1] <= nums2[i2]){
nums1[tail--] = nums2[i2--];
}else {
nums1[tail--] = nums1[i1--];
}
}
}
}
思路:
观察可知, nums1的后半部分是空的, 可以直接覆盖而不会影响结果, 所以可以将指针设置为从后向前遍历, 每次取两者之中的较大者放进nums1的最后面
6.环形链表
给定一个链表,判断链表中是否有环。
public class Solution {
public boolean hasCycle(ListNode head) {
if(head == null || head.next == null)return false;
ListNode fast = head;
ListNode slow = head;
while (fast != null) {
fast = fast.next;
if (fast != null) {
fast = fast.next;
}
if (fast == slow) {
return true;
}
slow = slow.next;
}
return false;
}
}
思路:
定义快慢指针,快指针走的速度是慢指针的两倍,如果两个指针从起点走,最终还能遇到的话说明链表存在环
7.通过删除字母匹配到字典里最长单词
给你一个字符串 s 和一个字符串数组 dictionary ,找出并返回 dictionary 中最长的字符串,该字符串可以通过删除 s 中的某些字符得到。
class Solution {
public String findLongestWord(String s, List<String> dictionary) {
int n = s.length();
String ans = "";
for (String sl : dictionary) {
int m = sl.length();
int p = 0, q = 0;
while (p < n && q < m) {
if (s.charAt(p) == sl.charAt(q)) {
q++;
}
p++;
}
if (q == sl.length()) {
if (sl.length() == ans.length()) {
ans = sl.compareTo(ans) < 0 ? sl : ans;
} else {
ans = sl.length() > ans.length() ? sl : ans;
}
}
}
return ans;
}
}
问题:
- 如何判断 dictionary 中的字符串 t 是否可以通过删除 s 中的某些字符得到;
- 如何找到长度最长且字典序最小的字符串。
思路:
- 定义一个记录结果的字符串,由于结果存在多种可能,所以用于计算最后保留下来的结果
- 取出集合中的每个小字符串,定义大字符串和小字符串的索引
- 在不越界的条件下比较他们的每一个字符,当大小字符串对应的字符相等时,小字符串索引右移,否则,大字符串索引右移
- 当小字符串索引到达最后一个字符时,我们进行对第二个问题的判断
- 如果当前字符串长度和之前保存的答案的长度不相等,我们将结果字符串取最长的那个字符串
- 如果当前字符串长度和之前保存的答案的长度相等,结果字符串取当前字符串与之前字符串的ASCII码差值
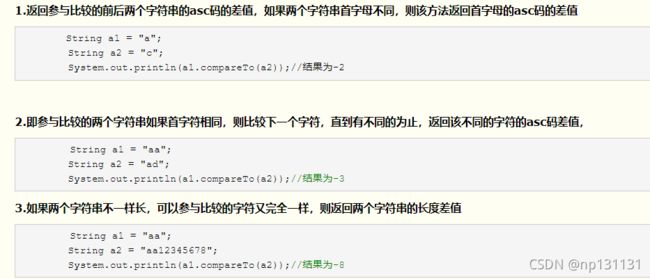
根据compareTo方法 ( 2 )能得到字典序最小的字符串
双指针总结
核心总结
1. 常常解决的问题:
- 快慢指针解决链表问题
- 左右指针解决数组或字符串相关的问题
- 双指针可以根据循环条件,设置查找步数
- 问题的分析结果往往是一个变量体内的两个部分,如数组中的某两个数,字符串中的某两个char
双指针的思想就是建立两个指针,这两个指针可以使相同方向,一般前进的速度不同或者两者的前进顺序不一致;也可能是相反的方向,通过使用相关的变量控制来达到我们的目的。
2.类型:快慢指针 & 左右指针
快慢指针
1.判断有无环:快指针一步走两个,慢指针一步一个,如果有环,最后指针会相遇;如果无环快指针先遇到null;
2.快慢指针可以寻找链表的中点(左右指针也可以)
3.相差问题,寻找链表的倒数第k个元素
快指针先走k步,然后快慢指针同时同速前进,当快指针遇到null时,慢指针到达倒数第k个节点。
左右指针
1.二分查找、有序的两数之和、反转数组
2.快速排序
第三章 排序
排序总结
1.排序类型
- 排序主要分为:内部排序和外部排序
①★内部排序:使用内存的排序
②*外部排序:使用内外存结合 - 内部排序:★八大排序
插入排序:直接插入排序和希尔排序
选择排序:简单选择排序和堆排序
交换排序:冒泡排序和快速排序
归并排序
基数排序
2.排序题常见的难点
- 边界的选取
- 循环条件的选取
- 堆排序、桶排序、归并排序
1.直接插入排序
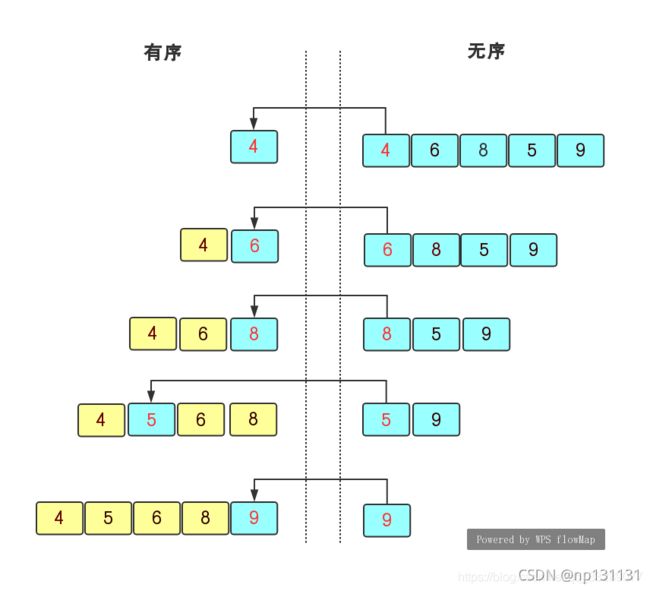
思路:
将每个元素逐个插入,先将先记录有序表的最后一个数,用无序表的第一个数与有序表的每个元素逐个比较。如果无序表中的拿到的数大于有序表中第一个数的话,就进行互换
public static void InsertSort1(int[] arr) {
int temp,i,j;
for (i = 1; i < arr.length; i++) {
//待插入元素从第二个数开始
for (j = i - 1; j >= 0 && arr[j] > arr[j + 1]; j--) {
//在满足指针非空且当前数大于前一个数时,全部一个个交换
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
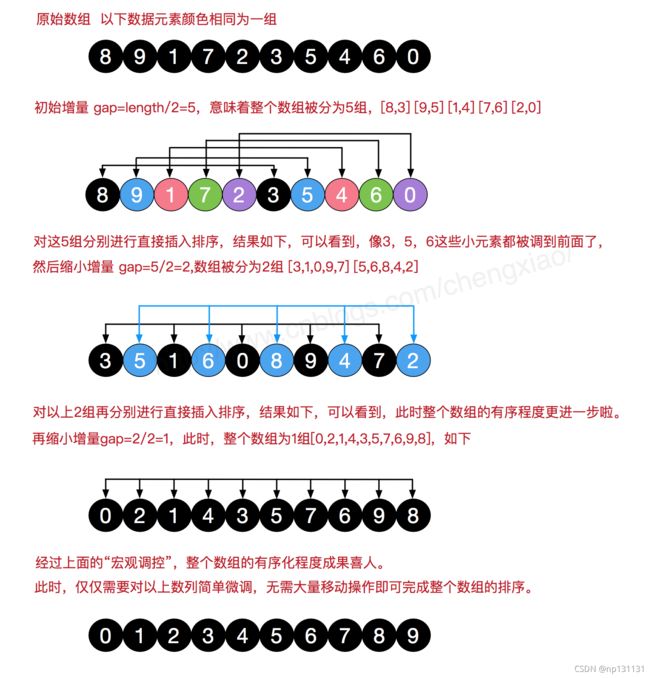
2.希尔排序
public static void shellSort(int[] arr){
for (int gap = arr.length / 2; gap > 0; gap /= 2) {
//分gap组
for (int i = gap; i < arr.length; i++) {
//在gap确定时,分小组
for (int j = i - gap; j >= 0; j -= gap) {
//比较每一小组的两个数的大小
if(arr[j] > arr[j + gap]){
int temp = arr[j];
arr[j] = arr[j + gap];
arr[j + gap] = temp;
}
}
}
}
}
3.简单选择排序
先找出数组中最小的,拿最小的和第一个值比较,小的放到最前面
public static void selectSort(int[] arr){
for(int i = 0; i < nums.length - 1; i++) {
//遍历长度-1次
for(int j = i + 1; j < nums.length; j++) {
if(nums[i] > nums[j]) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}
}
}
4.堆排序
基于对这种数据结构,即根节点的值大于所有孩子结点的值。堆排序的两大步骤:
①将无序序列构建成一个堆,根据升序降序需求选择大顶堆或小顶堆
②将堆顶元素与末尾元素交换,将最大元素"沉"到数组末端
③重新调整结构,使其满足堆定义,然后继续交换堆顶元素与当前末尾元素,反复执行调整+交换步骤,直到整个序列有序
public static void adjustheap(int[] arr, int i,int length){
int temp = arr[i];//先取出当前元素的值,保存在临时变量
for (int k = 2*i + 1; k < length; k=2*k+1) {
//k = i * 2 + 1 k 是 i节点的左子节点
if(k+1 < length && arr[k] < arr[k+1]){
//如果左子节点小于右子节点,就把指针指到右子节点上
k++;//即k++
}
if(temp < arr[k]){
//此时k在右子节点上,如果右子节点的数大于当前的节点的数
arr[i] = arr[k];//就把右子节点(大数)给到子树根(也就是一开始的当前节点,小数)
i = k;//指针i此时指在右子节点上
}else{
break;//如果子节点比根节点小,就不管,不操作
}
arr[i] = temp;//此时将小数给右子节点,完成互换
}
}
/**
* 功能:完成将以i对应的非叶子结点的树调整成大顶堆
* @param arr 待调整的数组
* @param i 表示非叶子结点在数组中索引
* @param length 表示对多少个元素继续调整, length是在逐渐的减少
*/
public static void heapsort(int[] arr){
int temp = 0;
for (int i = arr.length / 2 - 1; i >= 0; i--) {
//大顶堆的构建要经历(非叶子节点的个数)次
adjustheap(arr,i,arr.length);
}
for (int i = arr.length - 1; i > 0; i--) {
//一共排序要经历(数组长度-1)次
temp = arr[i];
arr[i] = arr[0];
arr[0] = temp;//此时把大顶堆上的大数和数组的第一个(最小的数)互换
adjustheap(arr,0,i);
}
}
5.冒泡排序
思路:
- 外层循环是冒泡排序要经历数组长度-1次遍历,而内层循环指的是指针从新的位置开始遍历,判断当前数和下一个数的大小
- 两个数进行比较,如果后数大于前数,加通过中间数(temp)进行交换
- 如果没有进行交换就说明,数组是按顺序排列的,此时直接跳出内层循环,即开始新的位置遍历
public static void bubble(int []arr){
int temp = 0;
for (int i = 0; i < arr.length - 1; i++) {
//经历长度-1次
for (int j = 0; j < arr.length - 1 - i; j++) {
//在去掉i的区间里交换数即可
if (arr[j] > arr[j + 1]) {
temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
}
}
}
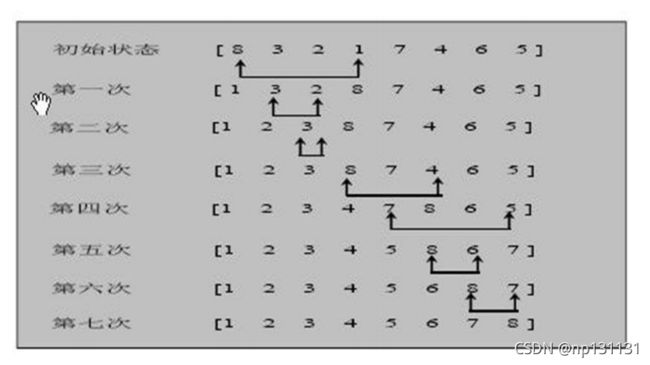
6.快速排序
public static void quicksort(int arr[], int left, int right) {
int l = left;//左指针
int r = right;//右指针
int pivot = arr[(left + right) / 2];//基准值
int temp = 0;
while (l < r) {
while (arr[l] < pivot) {
//左指针对应数小于基准值
l += 1;//左指针右移
}
while (pivot < arr[r]) {
//右指针对应数大于基准值
r -= 1;//右指针左移
}
if(l>=r){
//如果移着移着,左指针大于等于右指针,直接结束
break;
}
temp = arr[r];//左右指针指针移动完之后,进行数据交换
arr[r] = arr[l];
arr[l] = temp;
if (arr[r] == pivot) {
//如果此时的数和基准值相同
l += 1;
}
if (arr[l] == pivot) {
r -= 1;
}
}
// 如果 l == r, 必须l++, r--, 否则为出现栈溢出
if (l == r) {
r -= 1;
l += 1