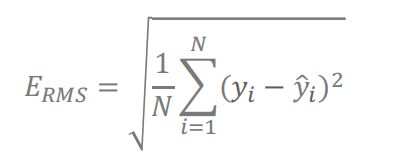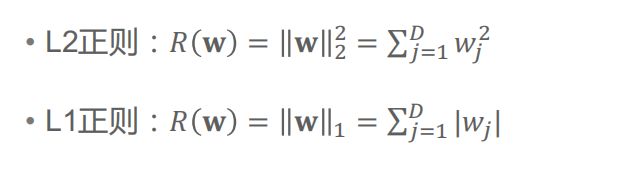过拟合
index:
- 机器学习中过拟合的概念
- 抑制过拟合的方法
过拟合
过拟合:模型过于复杂,在训练集上面的拟合效果非常好 甚至可以达到损失为0 但是在测试集的拟合效果很不好
欠拟合: 模型过于简单 在训练集和测试集的拟合的效果都不好
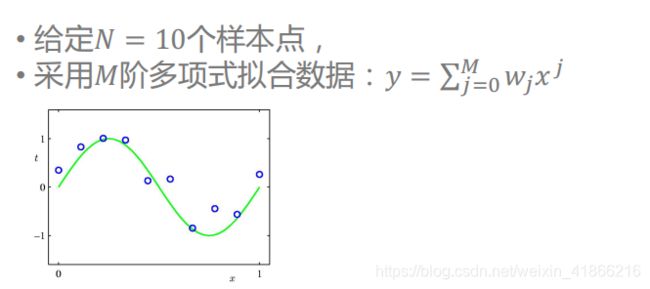
例: sin曲线拟合
数据产生模型是由sin函数和噪声组成的。 这个随机生成的噪声满足正太分布 均值为0 方差:0.003的平方
使用模型生成10个数据点 绿色代表函数 sin函数
关于多项式拟合:
当j=0时即用0阶多项式进行拟合 拟合的函数 是一条y=W0的直线
当j=1时即用1阶多项式进行拟合 拟合的函数 是y=W1x+W0 是一条有斜率 有截距的一次函数 形状是一条直线
当j=2时即用2阶多项式进行拟合 拟合的函数 是y=W2x²+ W1x+W0 是一条抛物线
以此类推 不同阶级的多项式拟合函数
下图为不同阶级的多项式拟合sin函数的图像:
由上图可以看出: 0阶多项式 和 1阶多项式 模型过于简单不能 拟合出sin函数的形状 这种现象叫做欠拟合
3阶多项式 刚好拟合出sin函数的图像 这样的拟合效果是理想中的效果
9阶多项式 模型过于复杂 虽然把图中所有的数据点都记住了 但是模型自身波动很大 对于新的数据不能有好的预测效果 这种现象叫过拟合。
也可以通过训练误差和预测误差的角度来分析模型的拟合程度:
注:公式中 开根号 是为了把数值 放在 与 y相同的量级上。
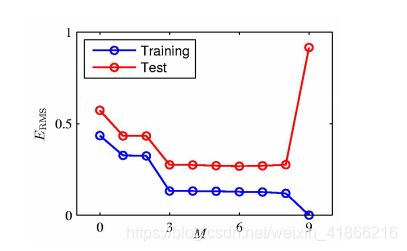
不同阶级的多项式函数在训练集和测试集上面的拟合效果
从上图可以看出:
从0到3 模型过于简单 训练集和测试集拟合的效果都不好
从3到8 : 3点模型达到了 拟合的效果 从3 往后 模型变的更加复杂 但是对于拟合的效果没有更好的提升 这块模型复杂度提升是不必要的 反而增加了 计算的复杂度 和 内存的占用。
从8到9 :模型更加复杂 完全拟合训练数据 但是在预测数据上面的预测误差大幅度的加大 这样的模型不能在新的数据上面有很好的预测效果 属于过拟合现象
评价模型性能的不应该在 在训练集的学习的效果上 而应该在新的数据(测试集)上的 预测能力上
这个叫 模型的泛化能力 也叫推广性。
不同拟合效果的参数
可以看到过拟合模型的参数 数值上是很大的,在图像上面显示就是即使x小幅度的变化 在预测残差上面 也会波动很大。
抑制过拟合的方法
1增加训练的样本数量
2在损失函数上面添加正则项
3改变数据生成模型的噪声生成的方差
在目标函数中增加正则
在给定有限训练样本数目时,可通过在目标函数中增加正则项减弱过
拟合现象
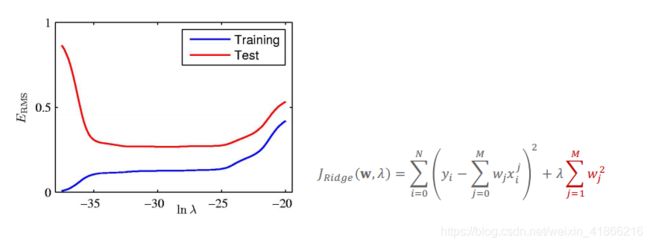
给定N = 10个样本点,目标函数中增加L2正则项,得到岭回归
(Ridge Regression)
岭回归系数(正则项系数):
• λ越大,回归系数(绝对值/平方)越小,模型越简单。
不同正则参数对应岭回归的训练误差 vs. 测试误差
λ越大,对模型复杂度惩罚越多,模型越简单,越不容易过拟合。
常用正则项
j是从1开始计算的,因为j=0时 W0对应的是截距项 正则项不对截距项进行惩罚。
还有一个正则是L0正则 他可以是一部分参数w 数值为0 从而起到 特征选择的效果
但是L0正则是一个np难问题 我们一般不使用L0正则
L1正则是L0正则在数学上的最优凸优化 因此L1正则 有着 和L0 相似的效果 即把部分参数压制到接近0 的效果。
还有一种减弱过拟合的另一种方法是减少数据的噪声。就是减小生成的数据的波动大小
一般情况下 生成数据的函数是固定的
样本的数量也可能是固定的
我们最常用的抑制过拟合的方法就是添加正则项