数据结构PTA 基础实验7-2.2 插入排序还是堆排序

题目

根据维基百科的定义：

插入排序是迭代算法，逐一获得输入数据，逐步产生有序的输出序列。每步迭代中，算法从输入序列中取出一元素，将之插入有序序列中正确的位置。如此迭代直到全部元素有序。

堆排序也是将输入分为有序和无序两部分，迭代地从无序部分找出最大元素放入有序部分。它利用了大根堆的堆顶元素最大这一特征，使得在当前无序区中选取最大元素变得简单。

现给定原始序列和由某排序算法产生的中间序列，请你判断该算法究竟是哪种排序算法？

输入格式：
输入在第一行给出正整数 N (≤100)；随后一行给出原始序列的 N 个整数；最后一行给出由某排序算法产生的中间序列。这里假设排序的目标序列是升序。数字间以空格分隔。

输出格式：
首先在第 1 行中输出Insertion Sort表示插入排序、或Heap Sort表示堆排序；然后在第 2 行中输出用该排序算法再迭代一轮的结果序列。题目保证每组测试的结果是唯一的。数字间以空格分隔，且行首尾不得有多余空格。

输入样例 1：

10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0

输出样例 1：

Insertion Sort
1 2 3 5 7 8 9 4 6 0

输入样例 2：

10
3 1 2 8 7 5 9 4 6 0
6 4 5 1 0 3 2 7 8 9

输出样例 2：

Heap Sort
5 4 3 1 0 2 6 7 8 9

解法一：不找规律，直接按照插入排序和堆排序的流程走一遍

思路
这种判断某一过程的序列是哪种排序的题目，总有一种“绝活”，那就是按照排序算法走一趟，每走一趟，就与给定的中间过程的序列进行比较，一旦相等，就打印结果，并且再走一趟排序，输出排序结果。
这种思路就是不得以而为之，因为它的时间复杂度和空间复杂度都很高，但是思路简单。

在能找到规律的前提下，不要使用这种方法

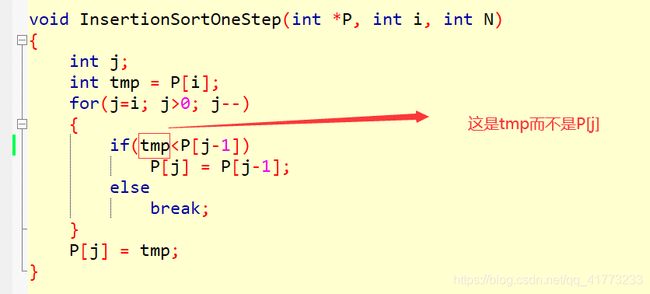
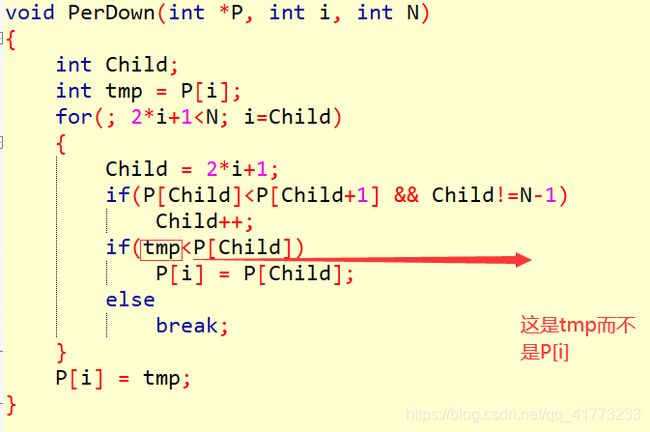
这里还是把这种算法列出来，作为巩固堆排序算法和插入排序算法。

堆排序算法和插入排序算法有一个小地方一定要注意：


实现

#include
#include

void Swap(int *a, int *b)
{
    int tmp = *a; *a = *b; *b = tmp;
}

void InsertionSortOneStep(int *P, int i, int N)
{
    int j;
    int tmp = P[i];
    for(j=i; j>0; j--)
    {
        if(tmp<P[j-1])
            P[j] = P[j-1];
        else
            break;
    }
    P[j] = tmp;
}

void ScanNumber(int *P, int N)
{
    for(int i=0; i<N; i++)
        scanf("%d", &P[i]);
}

void CopyArr(int *P1, int *P2, int N)
{
    for(int i=0; i<N; i++)
        P2[i] = P1[i];
}

int IsEqual(int *P, int *P1, int N)
{
    for(int i=0; i<N; i++)
    {
        if(P[i]!=P1[i])
            return 0;
    }
    return 1;
}

void ShowResult(int *P ,int N)
{
    printf("%d", P[0]);
    for(int i=1; i<N; i++)
        printf(" %d", P[i]);
}

void BuildHeap(int *P, int N)
{
    for(int i=(N-1)/2; i>=0; i--)
        PerDown(P, i, N);
}

void PerDown(int *P, int i, int N)
{
    int Child;
    int tmp = P[i];
    for(; 2*i+1<N; i=Child)
    {
        Child = 2*i+1;
        if(P[Child]<P[Child+1] && Child!=N-1)
            Child++;
        if(tmp<P[Child])
            P[i] = P[Child];
        else
            break;
    }
    P[i] = tmp;
}

//void HeapSortOneStep(int *P, int N);


int main()
{

    int N;
    scanf("%d", &N);
    int *P1 = (int *)malloc(N*sizeof(int));
    int *P2 = (int *)malloc(N*sizeof(int));
    ScanNumber(P1, N);
    CopyArr(P1, P2, N);

    int *CP = (int *)malloc(N*sizeof(int));
    ScanNumber(CP, N);


    //InsertionSort Test
    int i;
    int flag = 0;
    for(i=1; i<N; i++)
    {
        InsertionSortOneStep(P1, i, N);
        if(IsEqual(P1, CP, N))
        {
            flag = 1;
            break;
        }

    }

    if(flag == 1)
    {
        printf("Insertion Sort\n");
        InsertionSortOneStep(P1, i+1, N);
        ShowResult(P1 ,N);
    }
    else
    {
        BuildHeap(P2, N);
        for(i=N-1; i>0; i--)
        {
            Swap(&P2[i], &P2[0]);
            PerDown(P2, 0, i);
            if(IsEqual(P2, CP, N))
            {
                printf("Heap Sort\n");
                Swap(&P2[i-1], &P2[0]);
                PerDown(P2, 0, i-1);
                ShowResult(P2 ,N);
                break;
            }
        }
    }


    return 0;
}

解法二：找到插入排序和堆排序的本质区别

思路

1. 堆排序的本质是，从数组的最后一个元素开始，向前有序，当遇到某一个元素比第一个元素还小的时候，就说明这个元素还没进行堆的元素置换，也就是堆排序的下一步要对这个元素进行排列。且无序序列的部分与初始数组部分不一致
   比如在给的样例中：

10
3 1 2 8 7 5 9 4 6 0
6 4 5 1 0 3 2 7 8 9

9>6,8>6,7>6，但是2<6

2. 插入排序的本质是，从数组的第一个元素开始，向后有序。无序序列的部分与初始数组部分完全一致。

10
3 1 2 8 7 5 9 4 6 0
1 2 3 7 8 5 9 4 6 0

1<2<3<7<8, 8>5下一步要对5进行插入排序。

只要懂得以上的本质过程，此题就很简单了。
方法：

1. 检查给定的某一中间过程的序列，检查其无序部分，如果无序部分与初始序列相同，那么就是插入排序的结果，否则是堆排序。
2. 如果是插入排序，找到那个无序的初始点，就是P[j]>P[j+1]的那个j点。
3. 如果是堆排序，找到比P[0]小的点，即为下一步要进行的排序置换的点。

实现

#include
#include

void Swap(int *a, int *b)
{
    int tmp = *a; *a = *b; *b = tmp;
}

void InsertionSortOneStep(int *P, int i, int N)
{
    int j;
    int tmp = P[i];
    for(j=i; j>0; j--)
    {
        if(tmp<P[j-1])
            P[j] = P[j-1];
        else
            break;
    }
    P[j] = tmp;
}

void ScanNumber(int *P, int N)
{
    for(int i=0; i<N; i++)
        scanf("%d", &P[i]);
}



void ShowResult(int *P ,int N)
{
    printf("%d", P[0]);
    for(int i=1; i<N; i++)
        printf(" %d", P[i]);
}


void PerDown(int *P, int i, int N)
{
    int Child;
    int tmp = P[i];
    for(; 2*i+1<N; i=Child)
    {
        Child = 2*i+1;
        if(P[Child]<P[Child+1] && Child!=N-1)
            Child++;
        if(tmp<P[Child])
            P[i] = P[Child];
        else
            break;
    }
    P[i] = tmp;
}

int FindBeginIndex(int *CP, int N)
{
    for(int i=1; i<N; i++)
    {
        if(CP[i]<CP[i-1])
            return i;
    }
}

int FindHeapBeginIndex(int *CP, int N)
{
    for(int i=N-1; i>=0; i--)
    {
        if(CP[i]<CP[0])
            return i;
    }
}

int main()
{

    int N;
    scanf("%d", &N);
    int *P = (int *)malloc(N*sizeof(int));
    ScanNumber(P, N);

    int *CP = (int *)malloc(N*sizeof(int));
    ScanNumber(CP, N);


    //InsertionSort Test
    int k = FindBeginIndex(CP, N);
    int i;
    int flag = 0;
    for(i=k; i<N; i++)
    {
        if(P[i]!=CP[i])
        {
            flag = 1;
            break;
        }
    }

    if(flag == 0)
    {
        printf("Insertion Sort\n");
        InsertionSortOneStep(CP, k, N);
        ShowResult(CP, N);
    }
    else
    {
        printf("Heap Sort\n");
        k = FindHeapBeginIndex(CP, N);
        Swap(&CP[k], &CP[0]);
        PerDown(CP, 0, k);
        ShowResult(CP, N);
    }


    return 0;
}