算法(2)：排序算法-快速-归并-计数

一.快速排序

快速排序是一种非常高效的排序算法，采用 “分而治之” 的思想，把大的拆分为小的，小的拆分为更小的。其原理是，对于给定的记录，选择一个基准数，通过一趟排序后，将原序列分为两部分，使得前面的比后面的小，然后再依次对前后进行拆分进行快速排序，递归该过程，直到序列中所有记录均有序。

步骤：分解--递归--合并

设当前待排序序列为R[low:high]，其中low ≤ high，如果待排序的序列规模足够小，则直接进行排序，否则分3步处理。

1、分解

在R[low:high]中选定一个元素R[pivot]，以此为标准将要排序的序列划分为两个序列R[low:pivot-1]与R[pivot+1：high]，并使序列R[low:pivot-1]中所有元素的值小于等于R[pivot]，序列R[pivot+1：high]所有的值大于R[pivot]，此时基准元素以位于正确位置，它无需参加后续排序。

2、递归

对于子序列R[low:pivot-1]与R[pivot+1：high]，分别调用快速排序算法来进行排序。

3、合并

由于对序列R[low:pivot-1]与R[pivot+1：high]的排序是原地进行的，所以R[low:pivot-1]与R[pivot+1：high]都已经排好序后，不需要进行任何计算，就已经排好序。

注：基准元素，一般来说选取有几种方法

• 取第一个元素
• 取最后一个元素
• 取第中间位置元素
• 取第一个、最后一个、中间位置3者的中位数元素

写法1：不需要开辟新空间

实现方法：

1.取出第一个作为基准点（基准点位置空出（index）可作为后续排序的冗余位置）

2.左右指针(left，right)指向头尾，从右指针位开始比较，有小于基准点则赋值到基准点位置，right--，原右侧指针位空出位置成为index；然后从左指针比较有小大于基准则赋值到右侧空出位。

3.第一轮比完后，赋值基准值到index；index左右数组按步骤1进行（基准为不可参与下轮比较）

注意点：

1.递归退出的条件

2.当前基准值不能放在下一轮递归中，否则会出现死循环

3.基准点取出空位可作为

def fast_sort(nums,start,end):
    """
    快速排序
    :param nums:
    :return:
    """
    if start >= end: return
    point = nums[start]
    left = index = start
    right = end
    while left <= right:
        if index <= left:
            if nums[right] < point:
                nums[index] = nums[right]
                index = right
            right -= 1
        else:
            if nums[left] > point:
                nums[index] = nums[left]
                index = left
            left += 1
    nums[index] = point
    fast_sort(nums,start,index-1)
    fast_sort(nums,index+1,end)

写法2：需要开辟新空间

def quick_sort(b):
    """快速排序"""
    if len(b) < 2:
        return arr
    # 选取基准，随便选哪个都可以，选中间的便于理解
    mid = arr[len(b) // 2]
    # 定义基准值左右两个数列
    left, right = [], []
    # 从原始数组中移除基准值
    b.remove(mid)
    for item in b:
        # 大于基准值放右边
        if item >= mid:
            right.append(item)
        else:
            # 小于基准值放左边
            left.append(item)
    # 使用迭代进行比较
    return quick_sort(left) + [mid] + quick_sort(right)

二.归并排序

实现：

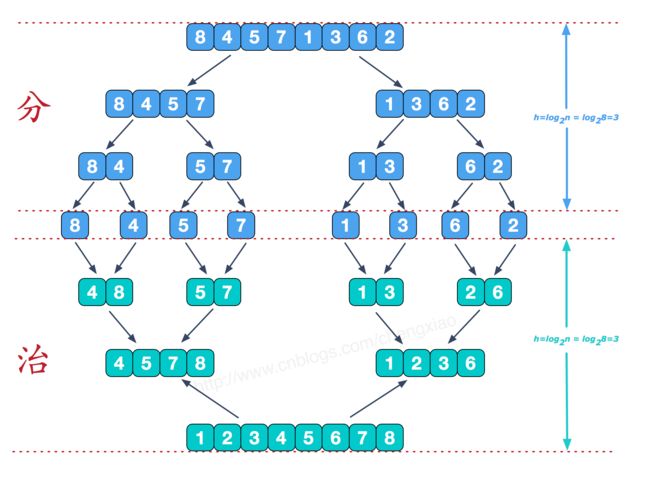
将大数组逐层拆分为小数组，将小数组排序后逐层合并成大数组。

实现方法：

1.实现一个有序数组合并函数merge，按上图治的过程就是合并有序数组

2.嵌套思想：

 

def merge_sort(nums):
    """
    归并排序
    :param nums:
    :return:
    """
    def merge(left,right):
        result = []
        left_i = right_i = 0
        l = max(len(left),len(right))

        while left_i < len(left) and right_i < len(right):
            if left[left_i] <= right[right_i]:
                result.append(left[left_i])
                left_i += 1
            else:
                result.append(right[right_i])
                right_i += 1
        while left_i < len(left):
            result.append(left[left_i])
            left_i += 1
        while right_i < len(right):
            result.append(right[right_i])
            right_i += 1
        return result

    l_nums = len(nums)
    if l_nums >1:
        num_l = nums[0:int(l_nums/2)]
        num_r = nums[int(l_nums/2)::]
        mx = merge_sort(num_l)
        my = merge_sort(num_r)   # 拆
        return merge(mx, my) # 合
        #return merge(merge_sort(num_l), merge_sort(num_r))
    else: # 拆到头了，返回
        return nums

三.计数排序

计数排序是非比较排序，只适用于数字数组排序，最好是最大最小值相差不大的数组

实现

1.找出原数组最大最小值

2.开辟新计数数组 长度为 最大值-最小值+1： 索引作为原数组值，值作为索引在原数组出现的次数

3.遍历计数数组，值不为0的位置都是原数组的值，将结果返回

def count_sort(nums):
    """
    计数排序
    :param nums:
    :return:
    """
    n_min = n_max = nums[0]
    for i in nums:
        if i < n_min: n_min = i
        if i > n_max: n_max = i
    ll = n_max - n_min +1
    count_list = [0]*ll
    for i in nums:
        count_list[i-n_min] += 1

    result = []
    for i in range(ll):
        for j in range(count_list[i]):
            result.append(i+n_min)
    return result

 参考：

图解排序算法(四)之归并排序 - dreamcatcher-cx - 博客园