Top K 问题的最优解 - 快速选择算法（图解详细教程）

Leetcode 215. Kth Largest Element in an Array

题意：给定一个无序的数组，寻找第K大的元素。

1.1：快速选择算法流程

输入：
nums = [3,2,1,5,6,4]
k=2

• step 1： 随机选择一个 pivot，通过一系列计算，查看是否是我们需要找到的 Top k 对应的 pivot
  
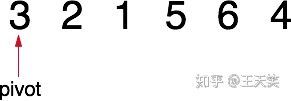
• step 2: 把 pivot 移动到最右的位置，以最右为标杆，从头开始对剩余部分进行选择查找
  
• step 3: 定义两个指针，初始化为0，查看 j 所在的指针是否小于等于 pivot，4 大于 3，所以我们把 j 指针右移一位
  
• step 4: 查看 j 所在的指针是否小于等于 pivot，2 小于等于 3，我们替换 i 指针和 j 指针所在的位置，同时把 i 和 j 指针都右移一位。
  
• step 5: 查看 j 所在的指针是否小于等于 pivot，1 小于等于 3，我们替换 i 指针和 j 指针所在的位置，同时把 i 和 j 指针都右移一位。
  
• step 6: 重复上述步骤，直到 j 指针移动到最右边
  
  
• step 7: 把pivot放到中间来，把数组划分为左右两个部分
  
• step 8: 此时 pivot 3 左边的值都小于 3，右边的值都大于 3，pivot 3 对应的是 Top 4 而不是 我们需要找的 Top 2，但我们可以知道，Top 2 一定在 pivot 3 右边的位置。
  
• step 9: 把右半部分按照重复执行上述步骤，最终找到 Top 2 的 pivot，对应的值为 5
  

1.2：注意事项

pivot 的选择很重要，如果对于一个已排序的数组，我们每次都选择最大/最小的值为 pivot，那么时间复杂度为 O(N^2) 。每次通过 random 选择 pivot 可以尽量避免最坏情况发生。

快速选择算法的平均时间复杂度是 O(N)，但最坏情况下的时间复杂度是 O(N^2) ，因为我们已经随机选择 pivot，所以能够最大程度上的减少最坏情况发生

1.3：python实现

def findKthLargest(self, nums, k):
	def quickSelect(nums, lo, hi, k): # 从小到大排序
        pivot = random.randint(lo, hi) # 0-len(nums)-1中随机取一个下标，避免最坏的情况
        nums[hi], nums[pivot] = nums[pivot], nums[hi] # 最右边存这个支点

        i = j = lo
        while j < hi:
            if nums[j] <= nums[hi]: # 找到一个比支点还小的数
                nums[i], nums[j] = nums[j], nums[i] # i, j相互交换
                i += 1
            j += 1 # 每一次j都要前进一步
        nums[i], nums[j] = nums[j], nums[i] # 把pivot放到中间来

        if hi > k + i - 1: # Topk在右边
            return quickSelect(nums, i + 1, hi, k) 
        elif hi < k + i -1: # Topk在左边
            return quickSelect(nums, lo, i - 1, k - (hi - i + 1))
        else:
            return nums[i]

    return quickSelect(nums, 0, len(nums)-1, k)

Leetcode 973. K Closest Points to Origin

1.1 题意

给定一个二维数组，数组中每一行代表一个点，求距离原点（0,0）最近的K个点

1.2 思路

还是按照以上的快速选择排序算法，稍微做一点点修改：

• 上一题的数组是从小往大排序，最后从右边开始数第K大的元素。
• 这一题是从大往小排序，最后从右边开始数K个小的元素，返回一个数组。

1.3 python实现

def kClosest(self, points, K):
	# 从小到大，找的是从右边数的第k大的元素
    def quickSort(points, lo, hi, k):
        pivot = random.randint(lo,hi)   #在闭区间里面选择
        points[hi], points[pivot] = points[pivot], points[hi]
        
        i = j = lo
        while j < hi: # 从左到右开始遍历
            if dis(points[j]) > dis(points[hi]): # 修改1：从大往小排序
                points[i], points[j] = points[j], points[i]  # 交换点i,j，把小数移到左边去
                i += 1
            j += 1
        
        points[i], points[j] = points[j], points[i]  # 把pivot放在中间来
        
        # 以下是根据pivot的位置来进行划分
        if hi > k + i -1: # i太小了，Topk在右边
            return quickSort(points, i+1, hi, k)
        elif hi < k + i - 1: # Topk在左边
            return quickSort(points, lo, i-1, k-(hi-i+1))
        else:
            
            return points[i:][:]  # 修改2：返回最后的k个最近的点
    
    def dis(dot): # 求得距离
        return dot[0]**2 + dot[1]**2
    
    return quickSort(points, 0, len(points)-1, K) # 要的是从左往右的点

3. 牛客：最小的K个数

链接：最小的k个数

3.1 题意：

输入n个整数，找出其中最小的K个数。例如输入4,5,1,6,2,7,3,8这8个数字，则最小的4个数字是1,2,3,4。

3.2 分析

这道题和上一道题"距离原点最近的k个节点"非常类似，因此也可以使用快速选择算法来做，并且时间复杂度很低，O(N)来做了

3.3 python实现

import random
class Solution:
    def GetLeastNumbers_Solution(self, tinput, k):
        # write code here
        if k <=0 or k > len(tinput) or not tinput: return []
        
        def quickSelect(nums, lo, hi, k): # 从小到大排序
            pivot = random.randint(lo, hi) # 0-len(nums)-1中随机取一个下标，避免最坏的情况
            nums[hi], nums[pivot] = nums[pivot], nums[hi] # 最右边存这个支点

            i = j = lo
            while j < hi:
                if nums[j] > nums[hi]: # 找到一个比支点还大的数
                    nums[i], nums[j] = nums[j], nums[i] # i, j相互交换，把大数放后面
                    i += 1
                j += 1 # 每一次j都要前进一步
            nums[i], nums[j] = nums[j], nums[i] # 把pivot放到中间来

            if hi > k + i - 1: # Topk在右边
                return quickSelect(nums, i + 1, hi, k) 
            elif hi < k + i -1: # Topk在左边
                return quickSelect(nums, lo, i - 1, k - (hi - i + 1))
            else:
                return nums[i:]
        
        res = quickSelect(tinput, 0, len(tinput)-1, k)
        res.sort() # 可能退化为O(N^2)啊！
        return res

最后：heapq模块实现top N—nlargest()和nsmallest()函数

通过以上快速选择算法选择的top N个元素后，原来的数组的顺序已经打乱了，使用heapq模块取出top N个元素后，不会修改原来的数组的顺序！

>>> import heapq
>>> nums=[1,8,2,23,7,-4,18,23,42,37,2]
>>> print(heapq.nlargest(3,nums)) # 从大到小排序
[42, 37, 23]
>>> print(heapq.nsmallest(3,nums))  #从小到大排序
[-4, 1, 2]