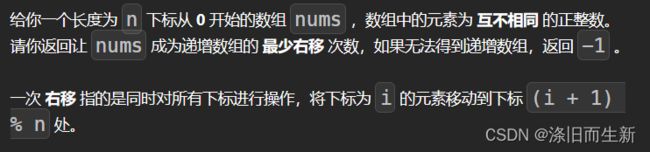
力扣第113场双周赛
前言
这场双周赛是我打得最差的一回,只做出来一道题,呜呜呜,我是个fw,下次继续加油吧!
2855. 使数组成为递增数组的最少右移次数
明确右移操作该如何进行:nums[-1:] + nums[:-1] 即可!
首先,构造出一个排序好的数组,进行0~n - 1次右移操作,每次操作后与有序数组进行比较,若相同则返回次数,否则继续,若超过n - 1次,就返回 -1!
class Solution:
def minimumRightShifts(self, nums: List[int]) -> int:
lst = sorted(nums)
n = len(nums)
cnt = 0
if lst == nums:
return 0
while 1:
if cnt == n:
return -1
tmp = nums[-1:] + nums[:-1]
if tmp == lst:
return cnt + 1
nums = tmp
cnt += 1
作为,第一题比赛的时候这样做,是无可厚非的,但比完赛就要思考有没有是什么更好的方法呢?
首先,看一下更优雅但未改进的方法(灵神的!)
class Solution:
def minimumRightShifts(self, nums: List[int]) -> int:
for i in range(len(nums)):
if all(x < y for x, y in pairwise(nums)):
return i
nums = nums[-1:] + nums[:-1]
return -1
那么,该怎么改进呢?
思考:如果最后可以使数组成为递增数组,那么一开始必定是这样两种情况!
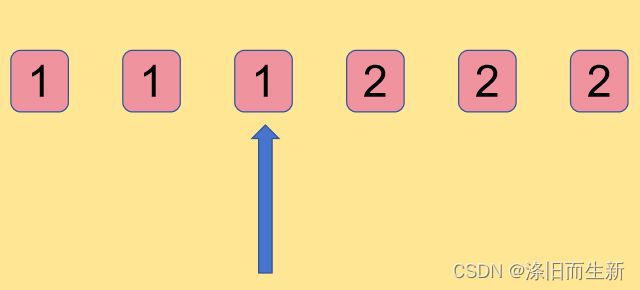
①一开始就是递增的;
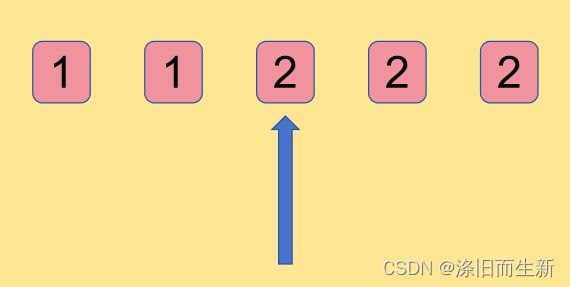
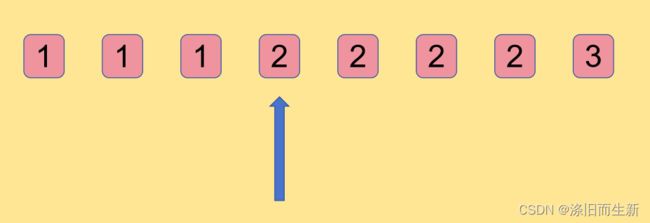
②有且仅有有两段递增序列,且第二段递增序列的值是最大值小于第一段递增序列的最小值!【如下图:3 < 4】

如果,我们找到大于两段递增序列的话,那么一定是不合法的,返回-1即可!
class Solution:
def minimumRightShifts(self, nums: List[int]) -> int:
i,n = 1,len(nums)
while i < n and nums[i - 1] < nums[i]:
i += 1
# 说明一开始就是递增序列,返回0!
if i == n:
return 0
# 如果第二段递增序列的值是最大值大于第一段递增序列的最小值,不合法,返回-1。
if nums[0] < nums[-1]:
return -1
x = i
i += 1
while i < n and nums[i - 1] < nums[i]:
i += 1
# 如果多余两段递增序列,那么返回-1。
if i < n:
return -1
return n - x
类似于这样的题,还有搜索旋转排序数组。
有兴趣的,可以去做一下,我贴一下代码,用到了不寻常的二分!
class Solution:
def search(self, nums: List[int], target: int) -> int:
left,right = 0,len(nums) - 1
while left <= right:
mid = left + right >> 1
if nums[mid] == target:return mid
if nums[0] <= nums[mid]:
if nums[0] <= target < nums[mid]:
right = mid - 1
else:
left = mid + 1
else:
if nums[mid] < target <= nums[-1]:
left = mid + 1
else:
right = mid - 1
return -1
2856. 删除数对后的最小数组长度
这种题目需要找规律,首先从特例出发!设数组的长度为n
特例:设出现次数最多的那个数是x,且个数为cnt
①如果 cnt > n // 2,那剩下 n - cnt 个数肯定可以与x组合进行删除,最后剩下的数肯定只有x了,其个数为:cnt - (n - cnt) = 2cnt - n
②如果 cnt = n // 2,这里还要判断,n是否为奇数,如果是的话,最后一定会剩下1个数,如果是偶数的话,一定什么也不剩了,x可以与剩下的所有数组合,删除!
③如果 cnt < n // 2,这种情况就要考验数学思维了!我们来具体分析一波!
我们将除了x之外的其他数,分成两堆 y 与 z,只要这两堆中的数没有相同的就可以了!
一定可以分成两堆,如果只有一堆的话,则有x + y = n;x < n // 2;y < n // 2;这与题意不符!
如下图所示,我们设x出现了7次,y出现了6次,z出现了5次

我们可以让y,z进行组合,直到y和z的和加起来小于等于 x(此处由于n为偶数,所以可以全部消去),进行一个状态的转换,使得第三种情况,转换成前面两种情况!
那么,我们可以不可以得到这样一个结论,y与z这两堆中的数进行组合消去后,一定可以使得y1 + z1 <= x呢?
答案是肯定的,我们来证明一波!
现有三堆元素,每一堆的元素数量分别为x,y,z,总数量为n;
【数量最大的是x;且x < n // 2;y > z;不同堆中的元素可以相互消除!】
只要,我们证明 y - z <= x即可,因为y与z这两堆的元素相互抵消后,最终剩下的元素的最小值为y - z,也就是把z给抵没了,如果满足的话,那么一定可以使 y1 + z1 == x 或者 y1 + z1 == x -1 (y1,z1为抵消后的数量,一开始 y + z > x),那样,就可以这道题了!
已知:x + y + z = n,x < n // 2,y + z > x,x > y > z;
求证:y - z <= x
证明如下:
假设,y - z > x;
则有,y > x + z
则有,y > n - y
则有,2y > n
则有,y > n // 2,则 y > x,这与题意矛盾,所以反证成功!
那么,这个题的代码就水到渠成了!
class Solution:
def minLengthAfterRemovals(self, nums: List[int]) -> int:
cnt,n = Counter(nums),len(nums)
# Python的collection.Counter的一个比较方便的操作!
x = cnt.most_common(1)[0][1]
if x > n // 2:
return 2 * x - n
else:
return n & 1
这里贴一个灵神大佬的神奇代码,巧妙利用二分,如果一个元素的数量大于等于 n // 2,这个数一定是最中间的那个数!
class Solution:
def minLengthAfterRemovals(self, nums: List[int]) -> int:
n = len(nums)
x = nums[n // 2]
max_cnt = bisect_right(nums, x) - bisect_left(nums, x)
return max(max_cnt * 2 - n, n % 2)
还有另一种方法,就是贪心。
贪心,每次选择数量最多的两个元素消除,这样保证可以最大程度的利用数量较多的元素进行消除!使用堆就可以了,注意Python中的是小根堆,加个负号就可以了!
class Solution:
def minLengthAfterRemovals(self, nums: List[int]) -> int:
cnt = Counter(nums).values()
heap = []
for x in cnt:
heappush(heap,-x)
while len(heap) >= 2:
m,n = -heappop(heap),-heappop(heap)
m -= 1
n -= 1
if m: heappush(heap,-m)
if n: heappush(heap,-n)
if len(heap) == 0:
return 0
else:
return -heap[0]
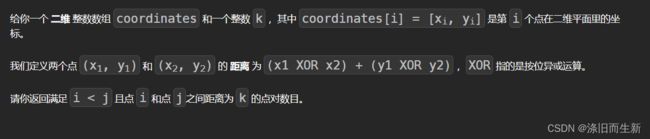
2857. 统计距离为 k 的点对
思路讲解
此题的关键在于数据范围,还有就是异或的性质,注意k的范围只有[0,100]
x1 ^ x2 + y1 ^ y2 = k
我们可以枚举 0 到 k
使得统计每一次枚举时,如果【x1 ^ x2 = i 以及 y1 ^ y2 = k - i】,累加!
如果这样枚举的话,需要O(n^2 * k)的时间复杂度,肯定会超时的!
注意:
x1 ^ x2 = i 可以推出 x1 ^ i = x2
这样的话:x1 ^ i = x2 、y1 ^ (k - i) = y2
每次枚举存储【x1,y1】在哈希表中,
我们只需要判断 【x2 ^ i,y2 ^ (k - i)】是否在已经存储过的哈希表中就可以了,如果哈希表中有【x2 ^ i,y2 ^ (k - i)】,那就累加!
两数之和的思想还是十分重要的!
代码就比较简单了:
class Solution:
def countPairs(self, coordinates: List[List[int]], k: int) -> int:
cnt = Counter()
ans = 0
for x,y in coordinates:
for i in range(k + 1):
ans += cnt[x ^ i,y ^ (k - i)]
cnt[x,y] += 1
return ans
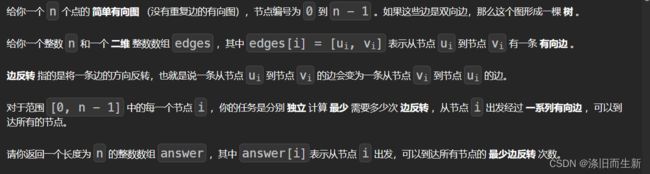
2858. 可以到达每一个节点的最少边反转次数
思路分析
我们首先思考,如果从节点0出发,到达所有节点的最少反转边次数该怎样做?
有两种思路:dfs、bfs
首先,我们建一个图
g = [set() for _ in range(n)]
for u,v in edges:
g[u].add(v)
# 如果,边相反的话就取相反数
g[v].add(-u)
我们先用dfs试一下
cnt = 0
vis = [0 for _ in range(n)]
def dfs(u):
global cnt
vis[u] = 1
for v in g[u]:
if vis[abs(v)]:continue
if v < 0:
cnt += 1
dfs(abs(v))
dfs(0)
print(cnt)
再用bfs试一波
cnt = 0
vis = [0 for _ in range(n)]
q = [0]
vis[0] = 1
while q:
q1 = []
for u in q:
for v in g[u]:
if vis[abs(v)]:continue
if v < 0:
cnt += 1
vis[abs(v)] = 1
q1.append(abs(v))
q = q1
print(cnt)
那么,如果我们对每个点都用一遍dfs或者bfs是否可以呢?
当然不可以,n最大为10**5,这样的时间复杂度是O(n ** 2)的,肯定不可以!
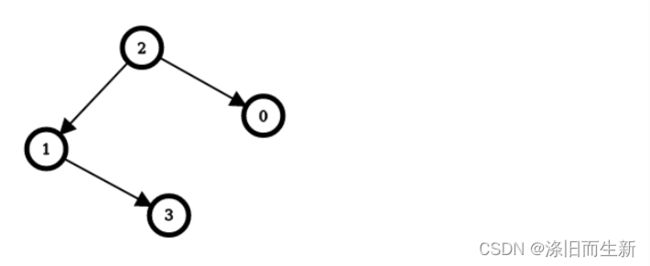
我们已经求得ans[0] = 1;
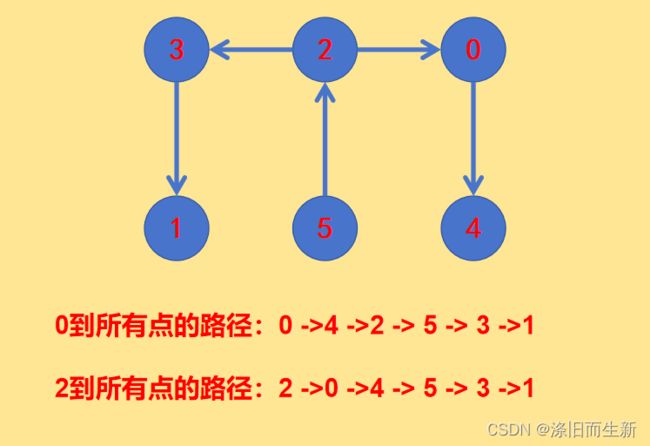
只需要反转0 - 2这条边,那么我们可以推出ans[2]吗?
实际上是可以的,我们只需要看2 到 0这条边是否需要反转就可以了,如果不需要反转的话,那么ans[2] = ans[0] - 1;如果需要反转的话,ans[2] = ans[0] + 1。
为什么,可以这样说呢?
因为,0到所有点与2到所有点不同的是只是在 2 - 0之间这一条路径上,其余的路径都是相同的!
所以,我们可以根据ans[0]把所有的ans[i]都给推出来,只需要看两个节点之间的边的方向就可以了!
class Solution:
def minEdgeReversals(self, n: int, edges: List[List[int]]) -> List[int]:
g = [set() for _ in range(n)]
for u,v in edges:
g[u].add(v)
# 如果,边相反的话就取相反数
g[v].add(-u)
ans = [0 for _ in range(n)]
vis = [0 for _ in range(n)]
def dfs(u):
vis[u] = 1
for v in g[u]:
if vis[abs(v)]:continue
if v < 0:
ans[0] += 1
dfs(abs(v))
dfs(0)
vis = [0 for _ in range(n)]
def dfs1(u):
nonlocal vis
vis[u] = 1
for v in g[u]:
if vis[abs(v)]:continue
# 说明 v -> u 是顺边
if v < 0:
ans[-v] = ans[u] - 1
# 说明 v -> u 是逆边,因为 u -> v 是顺边!
else:
ans[v] = ans[u] + 1
dfs1(abs(v))
dfs1(0)
return ans
同时,这个题我们还有一个思路,那就是通过一遍bfs,维护所有点到0之间的距离step,以及该点到0之间的路径需要反转的边数cnt!
那么,ans[i] = ans[0] - cnt + (step - cnt) = ans[0] + step - 2cnt
ans[0] - cnt 表示在 0 到 i 路径之外的需要翻转的数量!
step - cnt 表示在 0 到 i 路径之内的需要翻转的数量!
其代码如下所示:
class Solution:
def minEdgeReversals(self, n: int, edges: List[List[int]]) -> List[int]:
ans = [0 for _ in range(n)]
g = [set() for _ in range(n)]
for u,v in edges:
g[u].add(v)
g[v].add(-u)
# vis[i][0]表示0与i之间的距离step,vis[i][1]表示0与i之间的需要翻转的边的数量!
vis = {0:(0,0)}
# q里存的是,节点和需要翻转的边的数量;【距离可以通过step来维护,因为是bfs,每一层加1】
# 相当于一个层序遍历了!
q = [(0,0)]
step = 1
while q:
q1 = []
for u,cnt in q:
for v in g[u]:
if v > 0 and v not in vis:
q1.append((v,cnt))
vis[v] = (step,cnt)
if v < 0 and -v not in vis:
q1.append((-v,cnt + 1))
vis[-v] = (step,cnt + 1)
ans[0] += 1
q = q1
step += 1
for i in range(1,n):
ans[i] = ans[0] + vis[i][0] - 2 * vis[i][1]
return ans
总结
终于写完了,这篇博客花了我4个小时,好在每道题都弄懂了,也学到了新的东西,加油!