计算鬼成像学习笔记一:简介
这里写目录标题
- 1 何为鬼成像?
-
- 1.1 传统光学成像:所见即所得
- 1.2 鬼成像:又称关联成像
-
- 1.2.1 桶探测器:
- 1.2.2 CCD
- 1.2.3 空间分辨率:
- 1.2.4 光源
- 1.2.5 纠缠光子
- 1.2.6 赝热光源
- 1.2.7 散斑
- 2 何为计算鬼成像?
- 3 鬼成像发展历程
- 4 鬼成像特点(相比较传统成像优点和缺点)
-
- 4.1 优点:
- 4.2 缺点:
- 5 影响鬼成像质量的因素与一步步发展
-
- 5.1 光源(散斑的产生与结构)
- 5.2 光路
- 5.2 系统优化与重构方法
- 问题汇总1
1 何为鬼成像?
1.1 传统光学成像:所见即所得
物体发出的光,经过光学系统,成立一个倒立的虚像,例如人眼、照相机、透镜等成像,都属于经典成像范畴,主要包括光源、物体、光学系统三部分。
光照在物体上,反射的光射入人眼视网膜成像。
1.2 鬼成像:又称关联成像
如图所示,用分光棱镜将光分为两束,一束光照在物体上称为信号光路(也称为物臂,有多种称呼),后面放置无空间分辨率的桶探测器D1,收集照射到物体后的反射,透射的总光强(得到一个数,记作D1)。
另一束直接照在CCD相机上,称为参考光路(也称为参考臂,有多种称呼)。CCD相机具有空间分辩率,对该光路横截面进行扫描得到空间分布信息(收集到的是一个矩阵信息,记作I1)
经过N次测量,将D1、D2、…Dn和I1、I2…In这些N组数据进行“关联运算”就可以恢复物体的像。这里的关联运算就属于算法的问题了,就是图像重构的问题。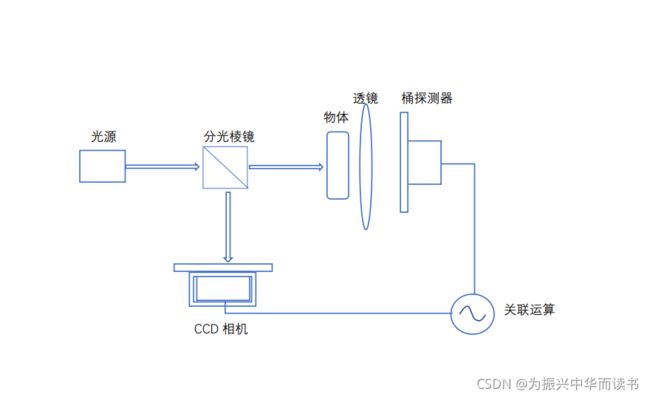
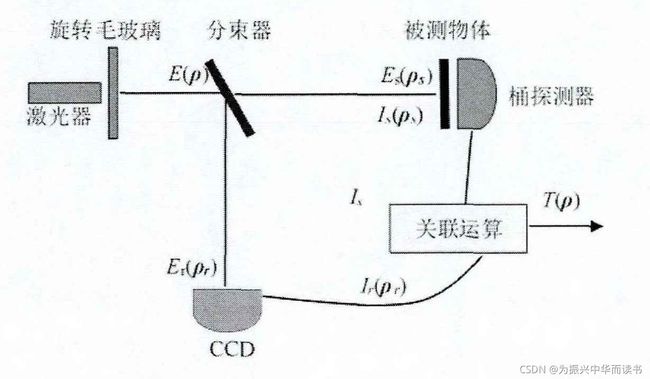
1.2.1 桶探测器:
暂且理解为 一个桶状探测器,收集所有方向的总光强信息。
1.2.2 CCD
CCD Charge coupled Device,中文全称:电荷耦合元件,可以称为CCD图像传感器。CCD是一种半导体器件,能够把光学影像转化为数字信号。
1.2.3 空间分辨率:
空间分辨率是指像素所代表的的地面范围的大小,即扫描仪的*瞬时视场,或地面物体能分辨的最小单元。
可以把空间分辨率理解为显示器分辨率,就是代表一个一个小格子,每个格子可以记录一个数据,那全部的数据不就是一个矩阵了。
1.2.4 光源
按照鬼成像的发展历程:纠缠双光子、赝热光源
1.2.5 纠缠光子
简单地说,纠缠光子就是两个光子不分你我,即使隔得很远,一个光子也能知道另一个光子的情况。
比如两个光子发生纠缠,你用一个光子照亮物体,另一个光子会符合的有关联现象发生
1.2.6 赝热光源
赝热光(pseudothermal light),又称伪热光,与真热光相对。
所谓的赝热光源,是由激光束照射在一块旋转的毛玻璃上,从而产生杂乱
的散射场。由于毛玻璃的表面较为粗糙,故会对经过的激光束产生较为明显,且杂乱无章的散射情况,从而产生近似于热光源的光强分布情况,即高斯随机分布的散射场,其光强-空间分布满足中心极限定理,赝热光也因此而得名。赝热光可以模拟真热光的光场统计性质,但相干性要比真热光好得多,因此更利于对热光的性质研究,在诸如鬼成像等对光场相干性的研究中广泛使用。
1.2.7 散斑
激光在散射体表面的漫反射或通过一个透明散射体(如毛玻璃)时,在散射表面或附近的光场中可以观察到一种无规分布的亮暗斑点,这种斑点称为激光散斑(Laser Speckles)。
无论是由激光打在毛玻璃上、还是SLM、还是DMD,形成的都是散斑,散斑就是光。这些散斑就可以理解为 整个鬼成像系统的光源。
由Matlab仿真出的散斑如图所示:
2 何为计算鬼成像?
上面讲到的鬼成像是由两条光路进行关联得到物体像的,其中任何一条光路单拿出来都不能得到物体的像。
而计算鬼成像只需要一条光路,就是信号光路,参考光路不需要了。
原理如下:
在上述讲到的热光鬼成像中,是利用激光照射在旋转的毛玻璃上可以产生赝热光。
还可以利用:SLM(空间光调制器)或DMD(数字微镜器件)这两个东西对光场进行相位或振幅调制,来产生赝热光。
热光鬼成像中,产生的赝热光场是无法通过计算得到的,因此参考光强只能通过CCD相机探测得到。但是在计算鬼成像中,SLM对光场的调制是可以控制的,调制产生的赝热光场分布是已知的。所以,赝热光自由传播一段距离后得到的参考光场可以按照公式计算得到,而不需要CCD进行探测。如此热光鬼成像中的参考光路便可以省去,变成了一条光路,如图所示。
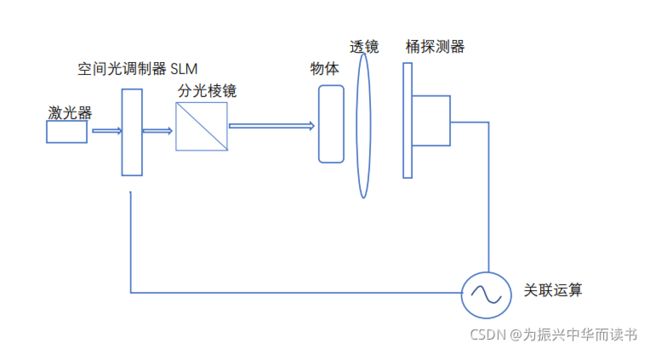
3 鬼成像发展历程
1956年
Hanbury Brown和Twiss
HBT实验:(Hanbury Brown和Twiss1956年Hanbury Brown和Twiss两哥们想测量天狼星的直径,怎么测呢?他们开始想用迈克尔逊干涉仪的方法测量,大家知道迈克尔逊干涉仪是根据两束光场E1和E2的干涉条纹来确定光程差(也就是距离的),既然是干涉条纹,那就需要两束光的相位要相干,而相位相干,我们把它叫做光场的一阶关联g(1)。但是天狼星离地球何止十万八千里,大概是8.6光年的样子,所以两束光的相位在到达地球后早就因为传播过程中的扰动而不相干了,所以根本测不出。于是,他俩一拍脑子,说既然光场E1和E2的关联测不到,那我们就测测他们光强I1(I1等于E1的平方)和I2的关联看看,也就是二阶关联g(2)。光强值相对于光场的相位信息来说稳定多了,经过积分求平均后,信号出现了。于是,他们不仅一年灌了两篇Nature(Nature 177, 27 (1956). Nature 178, 1046 (1956).),还从此成就了以自己名字命名的量子光学中的开山实验——HBT实验。
1963年
Glauber
在HBT实验的基础上 提出了光场的二阶关联函数,奠定了鬼成像的物理基础
1988年
Klyshko
理论上 提出了基于纠缠光子对的关联成像方案。
1995年
美国马里兰大学史砚华小组
实验上实现了纠缠双光子鬼成像
2001年
波斯顿大学A. F. Abouraddy
指出量子纠缠是实现量子成像的先决条件,由此引发了人们用经典光源实现鬼成像的实验研究和理论探讨
2002年-2005年
许多课题组
先后用赝热光源实现了鬼成像
如把激光照射到旋转着的毛玻璃上获得散斑场来进行实验
2006年、2012年又相继实现了空心阴极灯、太阳光等真热光源的鬼成像。
2008年
shapiro
从理论上提出了计算关联成像方案,使得单路的关联成像成为可能。
2009年
bromberg等人
在实验上实现了计算关联成像。
参考文献
[1]吴自文,邱晓东,陈理想.关联成像技术研究现状及展望[J].激光与光电子学进展,2020,57(06):9-25.
4 鬼成像特点(相比较传统成像优点和缺点)
4.1 优点:
(1)更强的抗干扰能力
由于传统成像是依据光的直线传播,汇聚在成像面上成像。
光线在传播过程中容易被干扰,而光强不会。
而关联成像是利用光强信息来得出物体的像所以抗干扰能力高。
2011 年,Shih 等人首次实现了抗大气湍流的鬼成像,实验结果显示,相较于传统成像,鬼成像对大气湍流所引起的干扰具有相当强的抵抗能力
散射介质也是影响成像质量的重要因素,因为光的散射会导致物体信息的严重丢失 ,同年,上海光机所的韩申生等人从理论上分析了散射介质对鬼成像成像质量的影响,并利用实验证明了相对于传统成像,鬼成像方案对散射介质所引起的干扰具有很高的抗性
(2)可以实现超分辨率成像
传统成像由于受到瑞利衍射极限的影响,分辨率很难提高,关联成像结合相关计算成像算法,可以突破瑞利衍射极限,实现高分辨率成像
衍射极限
简单来讲,按照几何光学的理论,一束理想的平行光波或球面波经过一个理想透镜后应该聚焦到一个无限小的点,而实际上由于衍射效应的存在,这个焦点不是无限小的,而是有一定直径的,这个直径跟波长、焦距和平行光光束直径有关,这就是衍射极限的结果。
这意味着什么呢?如果焦点是无限小的,就意味着物体上相邻很近的两个点经过透镜成像后仍然是可分辨的两个点,这样,只要我们的探测器或者眼睛分辨率足够高或者说像素足够小就总能看清楚这两个点。而如果焦点不是无限小的,而是有一定直径的,那么物体上相邻很近的两个点经过透镜成像后的两个点可能就会糊成一个点,这样即使探测器的分辨率再高也没办法分辨出来物体上的这两个点啦。聚焦光斑的大小也就是衍射极限决定了光学分辨率的极限。
(3)光源波长范围广
传统成像只能是可见光。而鬼成像其他波长的光源,例如X射线等等
4.2 缺点:
(1)采样时间长
一般需要采样少则需要2万次,正常则10万次,而假设采样1秒4次,那10万次需要 6.9个小时。
应用到运动的物体时,6.9个小时物体早不知道跑哪去了。
(2)成像质量差
算法带来的噪声使得成像质量相比传统成像差
由于传统成像是依据光的直线传播,汇聚在成像面上成像。
光线在传播过程中容易被干扰,而光强不会。
而关联成像是利用光强信息来得出物体的像所以抗干扰能力高。
2011 年,Shih 等人首次实现了抗大气湍流
的鬼成像[2],实验结果显示,相较于传统成像,鬼成像对大气湍流所引起的干扰具有相当强的抵抗能力
散射介质也是影响成像质量的重要因素,因为光的散射会导致物体信息的严重丢失 ,同年,上海光机所的韩申生等人从理论上分析了散射介质对鬼成像成像质量的影响,并利用实验证明了相对于传统成像,鬼成像方案对散射介质所引起的干扰具有很高的抗性
5 影响鬼成像质量的因素与一步步发展
根据鬼成像的原理图,可将系统分为三部分光源、光路和采样与算法
5.1 光源(散斑的产生与结构)
多体现在:对光源的特定调制,以及光斑的数学、统计模型的研究。
传统鬼成像中的的纠缠双光子和毛玻璃制备的赝热光源
计算鬼成像中的空间光调制器SLM或投影仪等“定制光源”
后人发现:光源的强度涨落剧烈程度直接关系到的鬼成像重构图像质量的好坏,使用强度涨落更加剧烈的光源进行鬼成像时,重构图像将具有更高的对比度和信噪比。
后人也对此展开了研究
2013年
程静、罗春伶等人
使用双曲余弦函数调制光源后,鬼成像的成像质量获得了提高。
2015 年
Shibuya 等人
研究了哈达玛成像,他们发现:哈达玛变换成像所获得的重构图像在信噪比,对比度等指标上均高于计算鬼成像
除此以外,
还有使用正弦变换图样的正弦变换鬼成像等改进方案。
5.2 光路
有透镜 无透镜
半波片
扩束器
光衰减片
偏振片
都有助于提高成像质量
5.2 系统优化与重构方法
(1)二阶关联重构(最原始最传统)
(2)高阶关联函数
利用光的高阶相关特性提出了高阶鬼成像,从理论上讲,使用高阶关联函数进行图像重构的高阶鬼成像可以获得更高的对比度。
(3)差分鬼成像
在进行研究时发现,用于恢复图像的二阶关联函数中含有一个常数背景项,从而降低了重构图像的对比度。Ferri 设计的差分鬼成像可以藉由去除二阶关联函数中的常数背景项,从而有效提高重构图像的质量。
(4)归一化鬼成像
这种归一化的二阶关联算法对时变噪声(主要是进行实验的时候外界的杂光干扰,或探测电路中的电磁干扰等不规则的、无法预测的噪声)具有更高的抵抗能力。
(5)对应鬼成像
(6)压缩感知算法重构
支持以少量测量就能恢复待测信号,打破了奈奎斯特采样定律的限制,前提是信号具有稀疏性
(7)基于傅里叶逆变换的重构
(8)基于矩阵运算的重构
(9)基于机器学习(深度学习)的重构