01背包问题——c

问题描述

给定n个重量为w1,w2,w3…wn，价值为v1,v2,v3…vn的物品和一个承重为w的背包，求这些午评中最有价值的子集，并且能够装到背包中。

蛮力法——穷举查找

穷举查找解决背包问题的大致思路

根据给出的n个物品的集合，考虑每种子集情况，计算出每个子集的总重量，是否满足总重量不超过背包的承重量，在满足条件的子集中找出价值最大的子集

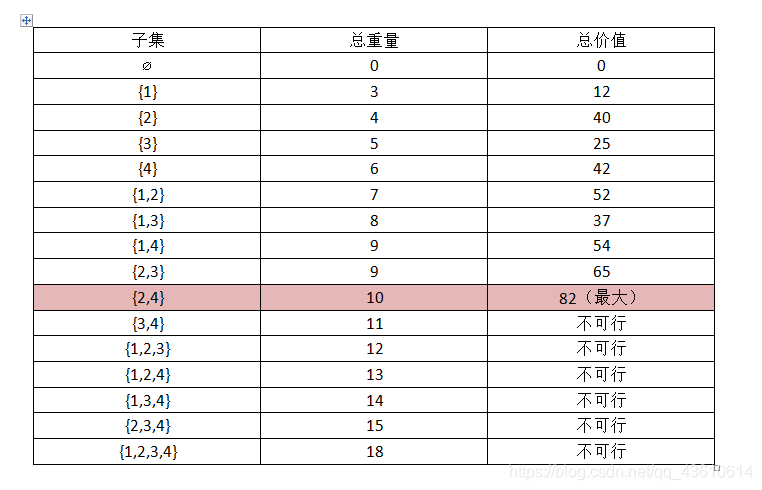
样例图解

背包承重量为：10

	物品1	物品2	物品3	物品4
重量(w)	3	4	5	6
价值(v)	12	40	25	42

由下图可知，最优为装入物品2,4。

分析

一个为n的序列，它的子集有2的n次方个。穷举的效率是非常低的，不推荐。

动态规划

递推公式

设计一个动态规划算法，需要推导出来一个递推公式。
在前i个物品中：
重量为：w1,w2,w3,…wi
价值为：v1,v2,v3,…vi
背包的承重量为：j
设F（i，j）为：当背包承重量为j时，在前i个物品中，总价值的最优解（也就是说能够放进重量为j的背包中的前i个物品中最有价值子集的总价值）

对于前i个物品来说，有三种情况：（前两种物品的重量小于背包的承重量）

1. 放入背包，被包含在最优解中，最优子集的价值为：F(i-1,j)（采用前i-1个物品的最优解）
2. 不放入背包，不被包含在最优解中，最优子集为：vi+F(i-1,j-wi)（放入时，背包还剩：j-wi，此时就要在j-wi的情况下，找到前i-1个物品的最优解）
3. 对于重量大于背包承重量的物品，肯定不用放入，最优子集的价值为：F(i-1,j)（采用前i-1个物品的最优解）

因此，在物品重量小于背包的称重量时，应当1,2的最大值，考虑要不要放进去

得到递推公式：

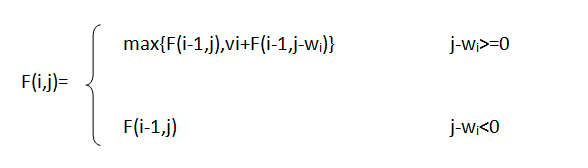
很明显，需要利用二维数组进行求解。
当i=0时，没有物品，最优子集F(i,j)也就等于0的；
当j=0时，背包承重量为0，最优F(i,j)还是等于0的。

于是得到初始条件：

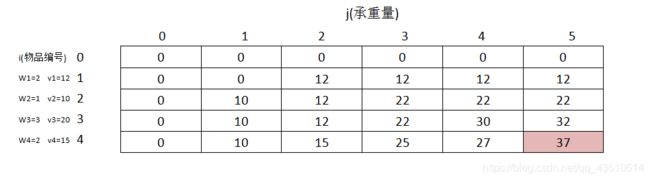
样例求解图解

知道递推公式之后，求解过程就相当于给一个二维数组填数字。
样例：背包承重量：W=5

物品	重量	价值
1	2	12
2	1	10
3	3	20
4	2	15

求解表如下：



在第五列最下面的一行为最大价值：37

关于选取的哪几个

求出了最大价值，当求有哪几个物品时，采用自底向上的方法，使用最后的结果和F(i-1,j)和vi+F(i-1，j-wi)进行比较，相等则选中。

c语言代码

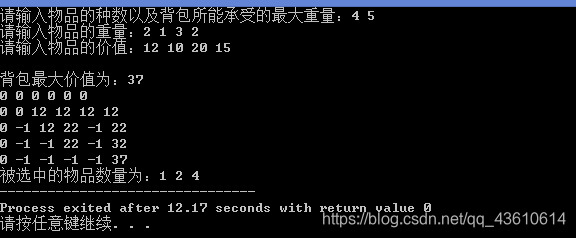
采用递推公式：

#include 
int num,c;//物品的种数，背包所能承受的重量 
int F[100][100],x[100];
void knapsackP1(int w[],int v[])//动态规划
	{
		int i=0,j=0,n;
		for(i=0;i<=num;i++)
		{	if(i==0)
				{
					for(j=0;j<=c;j++)	//初始化 
						F[i][j]=0;
				}
			else{
				for(j=0;j<=c;j++)
					{
						if(j==0)	//初始化 
							F[i][j]==0;
						else{
							if(j-w[i]>=0)	//递推公式 
								F[i][j]=F[i-1][j]>(v[i]+F[i-1][j-w[i]])?F[i-1][j]:(v[i]+F[i-1][j-w[i]]);
							else F[i][j]=F[i-1][j];
						}
					}
			}
			
		}
		for(i=num,j=c,n=0;i>=0;)	//	根据求得的结果，往上比较 
			{
			if(F[i][j]==F[i-1][j])//未放入 
				{
					i--;
				}
			else{	//放入 
				x[n]=i;
				n++;
				j=j-w[i];
				i--;
				}
			}
		printf("被选中的物品数量为："); 
		for(i=n-1;i>=0;i--)
			{
				printf("%d ",x[i]);
			}
			
	}
int main()
{
	printf("请输入物品的种数以及背包所能承受的最大重量：");
	scanf("%d%d",&num,&c);
	int i,w[c+1],v[c+1];
	printf("请输入物品的重量：");
	for(i=1;i<=num;i++)
		scanf("%d",&w[i]);
	printf("请输入物品的价值：");
	for(i=1;i<=num;i++)
		scanf("%d",&v[i]);
	knapsackP1(w,v);
	printf("\n背包最大价值为：%d",F[num][c]);
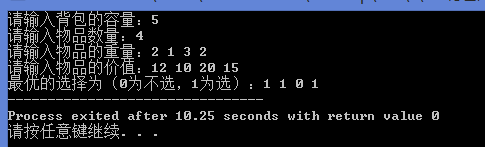
	return 0;
 } 

运行结果：

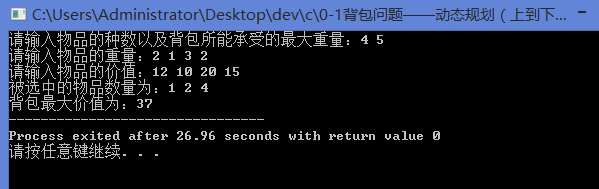
记忆化求解（仅供参考，代码可能有误，上面的代码更加好，不建议下面）

#include 
int num,c;//物品的种数，背包所能承受的重量 
int F[100][100],x[100],w[100],v[100];
int max(int a,int b)	//求最大值 
{
	if(a>=b)
		return a;
	else return b;
}
int knapsackP2(int i,int j)//动态规划——递归 
{	int value=0,v1,v2,n,m;
	if(F[i][j]<0)
		{
			if(j<w[i])
				{
					value=knapsackP2(i-1,j);
				}
			else{/*v2=v[i]+knapsackP2(w,v,i-1,j-w[i]);
					v1=knapsackP2(w,v,i-1,j);*/
					value=max(v[i]+knapsackP2(i-1,j-w[i]),knapsackP2(i-1,j));
			}
			
		}
	F[i][j]=value;
	for(n=0;n<=num;n++)
		{
			for(m=0;m<=c;m++)
				printf("%d ",F[n][m]);
			printf("\n");
		}
	return F[i][j];
}

int main()
{
	printf("请输入物品的种数以及背包所能承受的最大重量：");
	scanf("%d%d",&num,&c);
	int i,j,n;
	printf("请输入物品的重量：");
	for(i=1;i<=num;i++)
		scanf("%d",&w[i]);
	printf("请输入物品的价值：");
	for(i=1;i<=num;i++)
		scanf("%d",&v[i]);
	for(i=0;i<=c;i++)
		F[0][i]=0;
	for(i=0;i<=num;i++)
		F[i][0]=0;
	for(i=1;i<=num;i++)
		for(j=1;j<=c;j++)
			F[i][j]=-1;
	printf("\n背包最大价值为：%d\n",knapsackP2(num,c));
	for(i=0;i<=num;i++)
		{
			for(j=0;j<=c;j++)
				printf("%d ",F[i][j]);
			printf("\n");
		}
	for(i=num,j=c,n=0;i>=0;)	//	根据求得的结果，往上比较 
			{
			if(F[i][j]==F[i-1][j])//未放入 
				{
					i--;
				}
			else{	//放入 
				x[n]=i;
				n++;
				j=j-w[i];
				i--;
				}
			}
		printf("被选中的物品数量为："); 
		for(i=n-1;i>=0;i--)
			{
				printf("%d ",x[i]);
			}	
	return 0;
 } 

运行结果：

回溯

回溯的一般过程

对所有的可能的解都进行计算，利用二进制（000…00~111…11），计算出最大价值，存储最优解

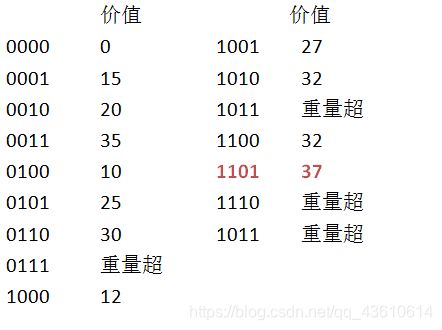
样例图解

样例：背包承重量：W=5

物品	重量	价值
1	2	12
2	1	10
3	3	20
4	2	15

0代表不装入，1代表装入：

c语言代码

#include 
#include 
int Bestvalue,weight,value,capacity;//分别是最大价值，每种情况的重量和价值，背包的容量   
void Backtrack(int w[],int v[],int best[],int x[],int n,int num)	//回溯 
{int i,j;
	if(n>=num)	//最多num个，到最后一个进行比较 
		{
			if(value>Bestvalue)//如果该种方法的价值能够超过最大价值则采用该方法 
				{
					Bestvalue=value;
					for(j=0;j<num;j++)		//保存采取的方法 
					{
						best[j]=x[j];
					}
				}
		}
	else{
		for(i=0;i<=1;i++)	//根据二进制01试可能的所有方法 
			{
			x[n]=i;		//各种方法 
			if(i==0)
				{
				Backtrack(w,v,best,x,n+1,num); 	//如果为零就递归到下一个 
				}
			else{
				if(weight+w[n]<=capacity)
				
					{
					weight+=w[n];		//选择就加上被选则物品的重量和价值 
					value+=v[n];
					Backtrack(w,v,best,x,n+1,num);
					weight-=w[n];		//每一种的方法算完之后减去被选中的重量和价值，可以使得每种方法的最开始的重量和价值都为0 
					value-=v[n];
					}
			}
		}
	}
} 
int main()
{	int num; 
	printf("请输入背包的容量：");
	scanf("%d",&capacity);
	printf("请输入物品数量：");
	scanf("%d",&num);
	int w[num],v[num],i,best[num],x[num];
	printf("请输入物品的重量：");
	for(i=0;i<num;i++)
		scanf("%d",&w[i]);
	printf("请输入物品的价值：");
	for(i=0;i<num;i++)
		scanf("%d",&v[i]);
	Backtrack(w,v,best,x,0,num);	
	printf("最优的选择为（0为不选，1为选）："); 
	for(i=0;i<num;i++)
		printf("%d ",best[i]);
	return 0; 
} 

运行结果：