数据结构—堆(C语言实现)
目录
堆是什么?
一、大堆
一、小堆
如何实现堆?
代码实现 ?
一、定义堆的结构体
二、初始化堆
三、构建堆
1.利用向下调整算法
2.开始构建
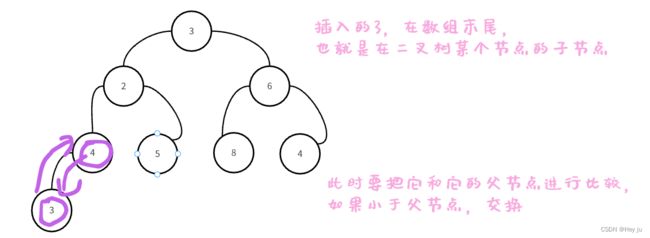
四、插入元素
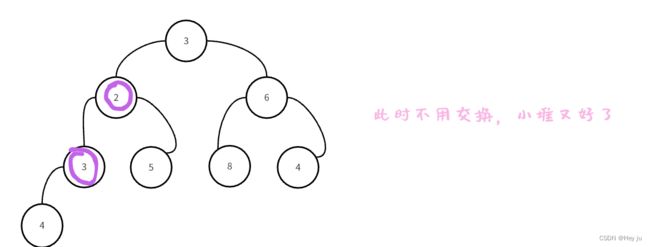
1.利用向上调整算法
五、取出堆顶元素、销毁堆
六、堆排序
Extra:TOP K 问题
堆是什么?
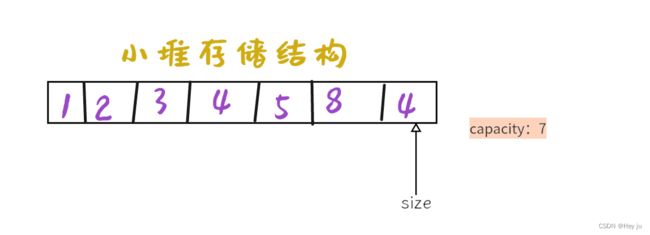
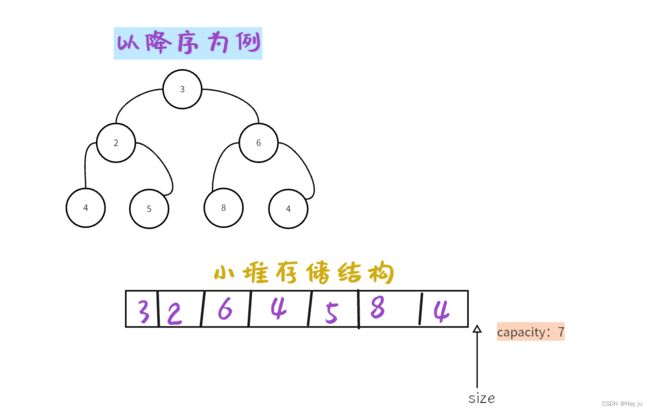
堆是数据结构的一种,它的逻辑结构是一个完全二叉树,存储结构是一个数组。
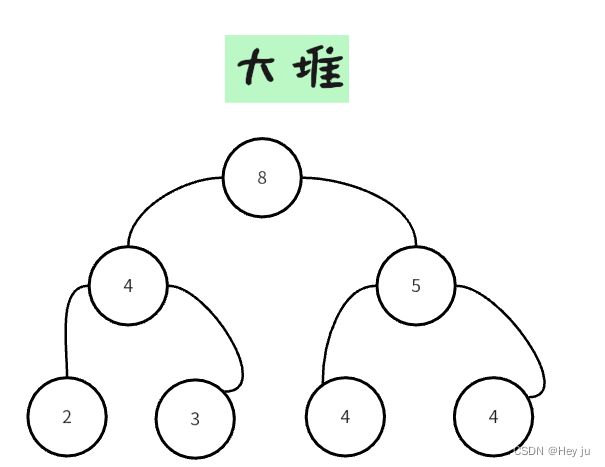
一、大堆
每个父节点都大于子节点
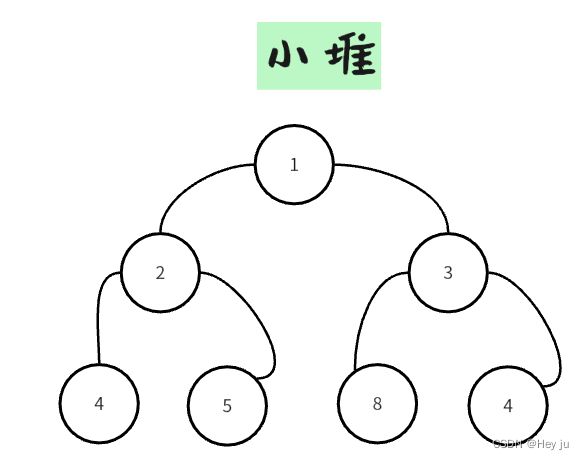
一、小堆
每个父节点都小于子节点
如何实现堆?
数组即可,利用完全二叉树的特点。(后面将不断用到)
代码实现 ?
一、定义堆的结构体
typedef int E;
typedef struct my_heap {
E* _heap;
int _size;
int _capacity;
}my_heap;二、初始化堆
void initiaze(my_heap* heap, E* arry, int n) {
assert(arry);
assert(heap);
heap->_heap = (E*)malloc(n * sizeof(E));
assert(heap);
heap->_capacity = n;
heap->_size = n;
memcpy(heap->_heap, arry, n * sizeof(E));//内存拷贝
}三、构建堆
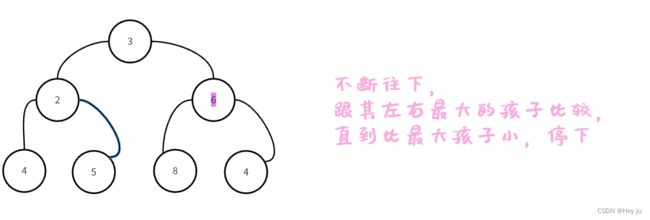
1.利用向下调整算法
//小堆-向下调整算法
void heap_down(my_heap* heap,int root) {
int parent = root;
int child = parent * 2 + 1;
while(child_size){
if (child + 1 _size && heap->_heap[child + 1] < heap->_heap[child]) {
child++;
}
if (heap->_heap[child] < heap->_heap[parent]) {
swap(&(heap->_heap[child]), &(heap->_heap[parent]));
parent = child;
child = child * 2 + 1;
}
else {
break;
}
}
}
2.开始构建
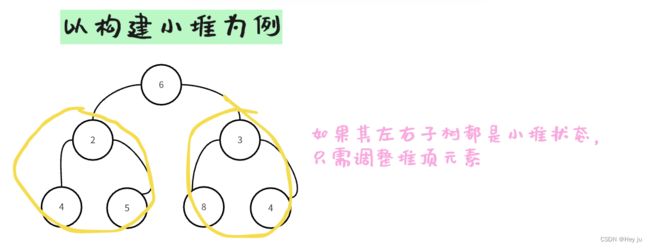
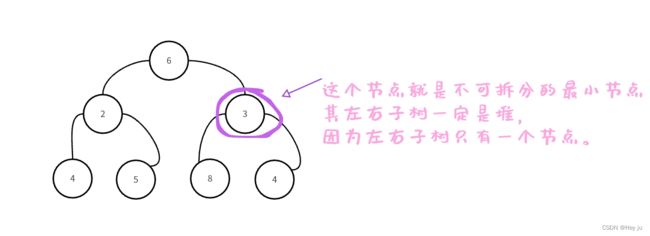
会向下调整算法还不够,向下调整算法只能用于左右子树都已经是堆的情况下。
而如何使每一颗左右子树都是堆,需要从最小不可拆分的节点开始,依次往前递推。
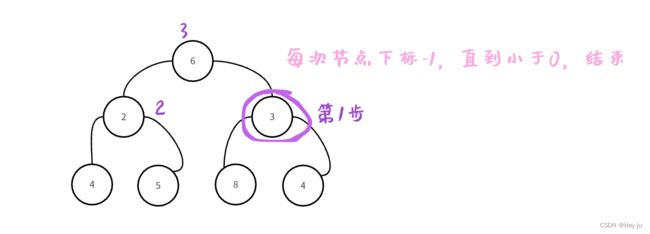
每次对这些节点使用向下调整算法,
//堆建立-小堆
void com_heap(my_heap* heap) {
assert(heap);
int i =0;
for (i= (heap->_size - 2) / 2; i >= 0; i--) {
heap_down(heap, i);
}
}四、插入元素
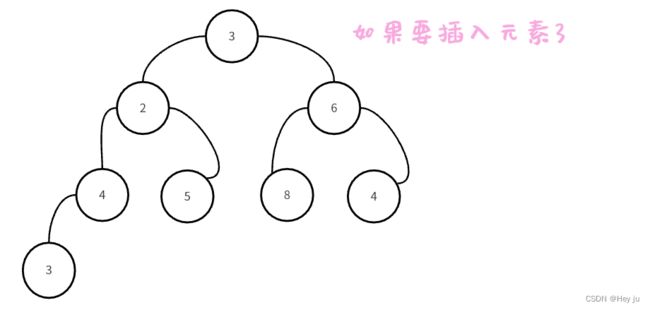
要保持小堆,除了可以用上面构建堆的方法,重新构建一次,但这样时间复杂度就太高了,这时就需要向上调整算法了。
1.利用向上调整算法
//向上调整算法
void heap_up(my_heap* heap,int child){
assert(heap);
int parent = (child-1)/2;
while(child>0){
if(heap->_heap[child]_heap[parent]){
swap(&(heap->_heap[child]), &(heap->_heap[parent]));
child=parent;
parent=(child-1)/2;
}else{
break;
}
}
}
//往堆中添加元素
void heap_push(my_heap* heap,E ele){
assert(heap);
//如果空间不够扩容,每次扩容为上次容量的两倍
if(heap->_size==heap->_capacity+1){
heap->_capacity *=2;
heap->_heap=realloc(heap,heap->_capacity*(sizeof(E)));
if(!heap)return;
}
heap->_heap[heap->_size++]=ele;
heap_up(heap,heap->_size-1);
} 五、取出堆顶元素、销毁堆
//从堆中取出元素,取出堆顶元素
E heap_hatch(my_heap* heap) {
assert(heap);
return heap->_heap[0];
}//堆销毁
void heap_destroy(my_heap* heap) {
assert(heap);
free(heap->_heap);
heap->_heap = NULL;
}六、堆排序
前面我们已经了解了构造堆,插入元素,如果要把这个数组的数从小排到大,能否使用堆来进行呢。
首先,我们要明白升序要大堆,降序要小堆。(后面解释)
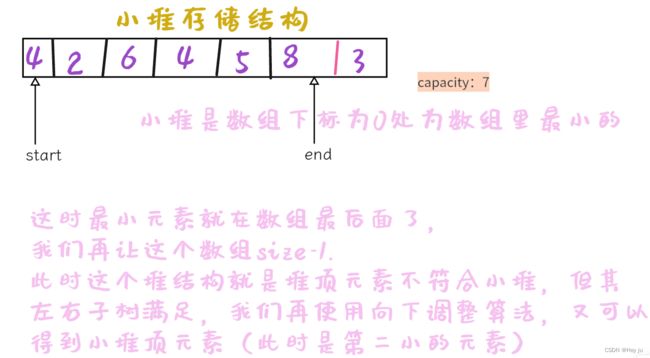
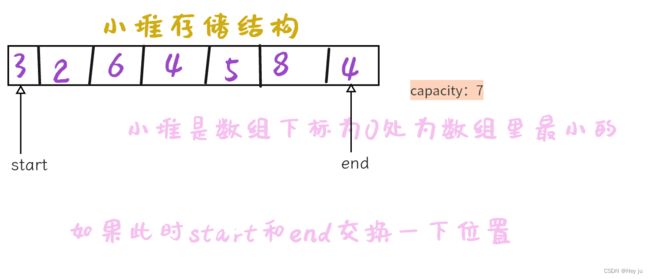
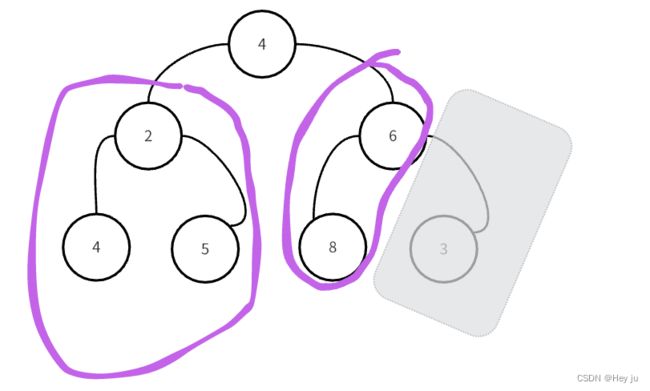 这就是堆排序的思想,不断拿到堆顶元素,放到数组最后,得到最小、第二小、第三小......的数字,实现降序,你也知道了为什么要使用大堆排升序,小堆排降序。
这就是堆排序的思想,不断拿到堆顶元素,放到数组最后,得到最小、第二小、第三小......的数字,实现降序,你也知道了为什么要使用大堆排升序,小堆排降序。
下面是升序代码:
//堆排序-升序
E* heap_sort(int *arry,int len) {
//建大堆
assert(arry);
if (len == 0)return NULL;
my_heap heap;
initiaze(&heap, arry, len);
com_heap_big(&heap);
//堆建好后,每次把堆最后一个元素与堆顶替换,再将堆大小减一,进行向下调整算法
int start = 0;
int end = len - 1;
while (end) {
swap(heap._heap + end, heap._heap + start);
end--;
heap._size--;
heap_down_big(&heap, 0);
}
memcpy(arry, heap._heap, len*(sizeof(E)));
heap_destroy(&heap);
return arry;
}Extra:TOP K 问题
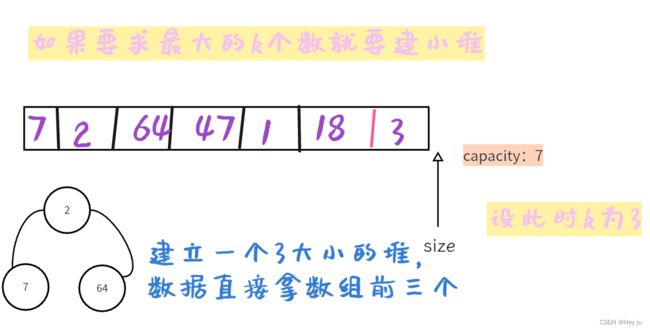
要求:从N个数中找到最小或最大的前k个数
相信你已经会了,那么要求最小的k个数就需要建立一个k个元素的大堆了。
//topk问题-最大k个数
int* top_k(int* arry,int len,int k) {
assert(arry);
//选数组前k个数组成k个元素的堆
int* heap_k = (int*)malloc(k * sizeof(int));//因为要把数组传出去,动态开辟
memcpy(heap_k, arry, k * sizeof(int));
//构建堆
my_heap heap;
heap._heap = heap_k;
heap._size = k;
heap._capacity = k;
com_heap(&heap);
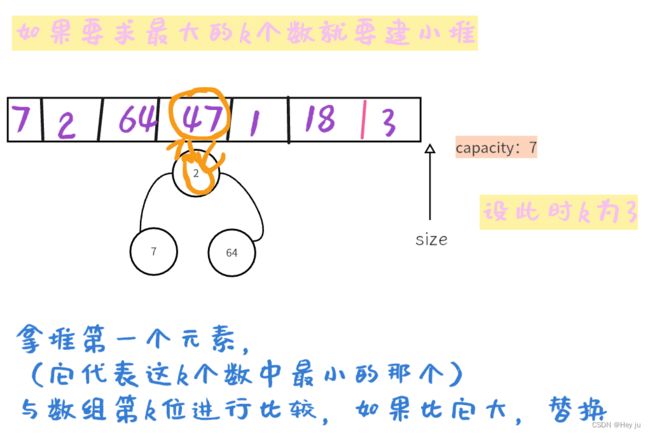
//依次拿堆顶元素与数组从k开始的元素进行比较
for (int i = k; i < len; i++) {
if (heap._heap[0] < arry[i]) {
swap(heap._heap + 0, arry + i);
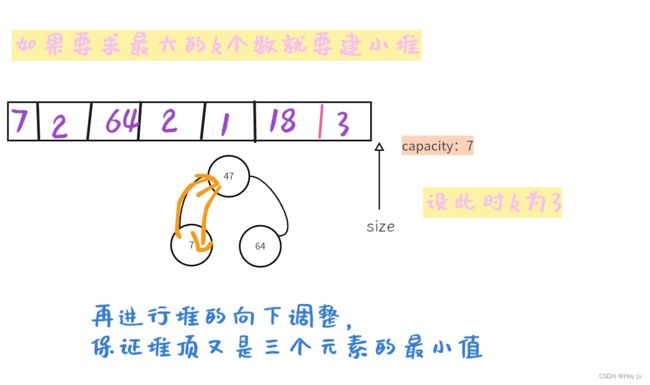
//向下调整
heap_down(&heap, 0);
}
}
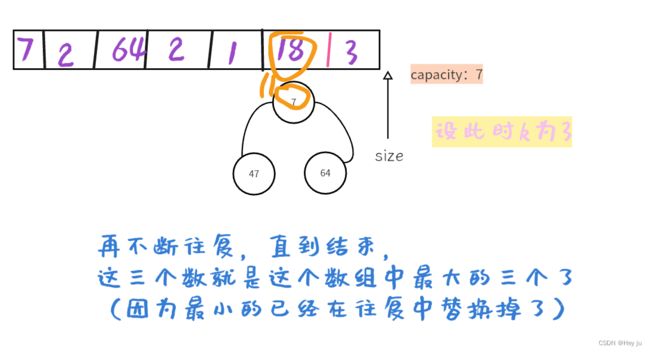
//此时heap里面的元素就是最大的k个数了
return heap._heap;
}