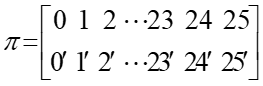密码学——常见的密码学习总结

目 录

1 基本概念（*）

2 密码分析学

3 密码分类

3.1 置换密码

3.2 代换密码

移位密码，替换密码，放射密码，希尔密码，维吉尼亚密码

3.3  分组密码

DES,AES,RSA

---

1 基本概念（*）

密码学又分为密码编码学（Cryptography）和密码分析学（Cryptanalysis）。

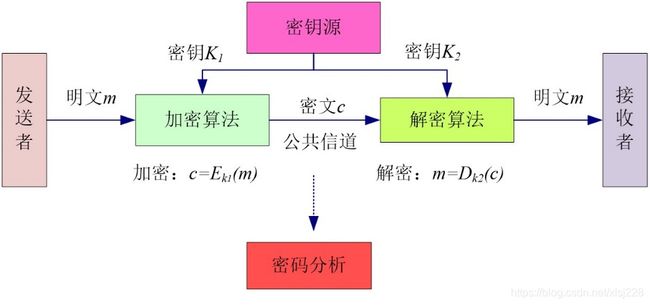
在密码学中，一个密码体制或密码系统是指由明文、密文、密钥、加密算法和解密算法所组成的五元组。

明文是指未经过任何变换处理的原始消息，通常用m(message)或p( plaintext)表示。所有可能的明文有限集组成明文空间,通常用M或P表示。

密文是指明文加密后的消息,通常用c(ciphertext)表示。所有可能的密文有限集组成密文空间.通常用C表示。

密钥是指进行加密或解密操作所需的秘密/公开参数或关键信息,通常用k(key)表示。所有可能的密钥有限集组成密钥空间，通常用K表示。

加密算法是指在密钥的作用下将明文消息从明文空间映射到密文空间的一种变换方法,该变换过程称为加密,通常用字母E表示，即c= EK(m)。

解密算法是指在密钥的作用下将密文消息从密文空间映射到明文空间的一种变换方法，该变换过程称为解密,通常用字母D表示，即m= DK(c)。

2 密码分析学

（1）唯密文攻击（Ciphertext only Attack）

（2）已知明文攻击（Known Plaintext Attack）

（3）选择明文攻击（Chosen Plaintext Attack）

（4）选择密文攻击（Chosen Ciphertext Attack）

（5）选择文本攻击(Chosen Text  Attack)

3 密码分类

3.1 置换密码

1）列变位法

I  n  f  o  r
m  a  t  i  o
n  S  e  c  u
r  i  t  y  T
e  c  h  n  o
l  o  g  y                      

密文是：ImnrelnaSicoftethgoicynyrouTo

2）矩阵变位加密

　1 2 3 4 5 6
　N e t w o r
　k  S e c u
　r i t y         

按5、2、6、4、1、3的列序重新排列，

密文为：oerwNtc uekS i yrt

3.2 代换密码

1）单表代换

（1）移位密码

K = 3 是凯撒密码

（2）替换密码

（3）仿射密码（*）

2）多表代换

（1）希尔密码（*）

解密方法

KM = C => K'KM = K'C 即M = K'C

所以要求出E的逆矩阵，根据AA' = E求。

（2）维吉尼亚密码（*）

3.3  分组密码

（1）对称密码体制：

K1=K2 或 K2=f（K1）

优点：

（a）加密和解密的速度都比较快，具有较高的数据吞吐率；

（b）对称密码体制中所使用的密钥相对较短；

（c）密文的长度往往与明文长度相同。

缺点：

（a）密钥分发需要安全通道，需要付出的代价较高；

（b）密钥量大，难于管理。

（2）非对称密码体制：

K1和K2不相同，且不能从公钥推出私钥，或者说从公钥推出私钥在计算上是不可行的 。

优点：

（a）密钥的分发相对容易。

（b）密钥管理简单。

（c）可以有效地实现数字签名。

缺点：

（a）与对称密码体制相比，非对称密码体制加解密速度较慢；

（b）同等安全强度下，非对称密码体制要求的密钥长度要长一些；

（c）密文的长度往往大于明文长度。

1）DES（*）

（1）基本算法

DES是对数据分组加密的分组密码算法，分组长度为64位。每64位明文加密成64位密文，没有数据压缩和扩展。

密钥长度为56位，若输入64位，则8，16，32，40，48，56，64位为奇偶校验位。

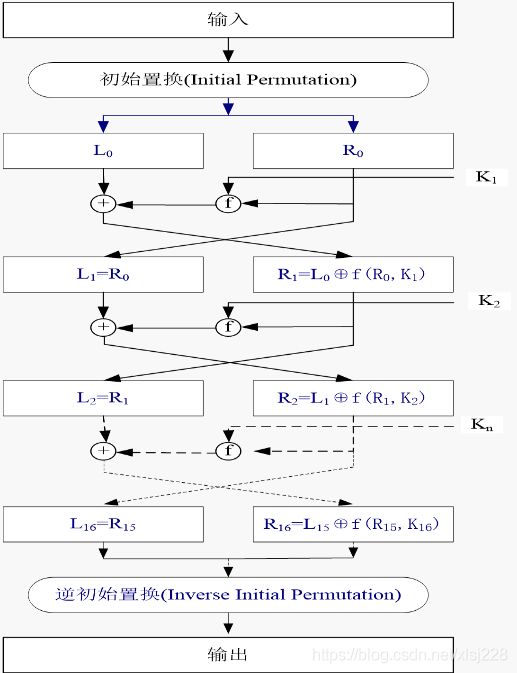
（2）流程描述

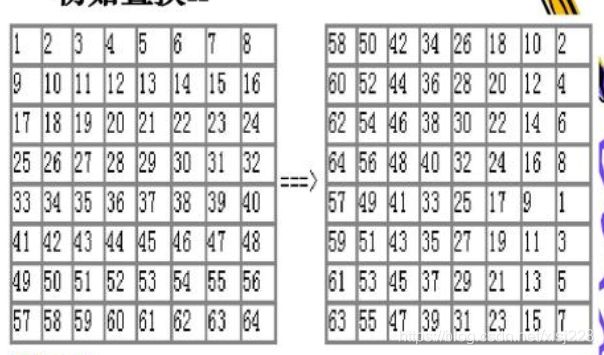
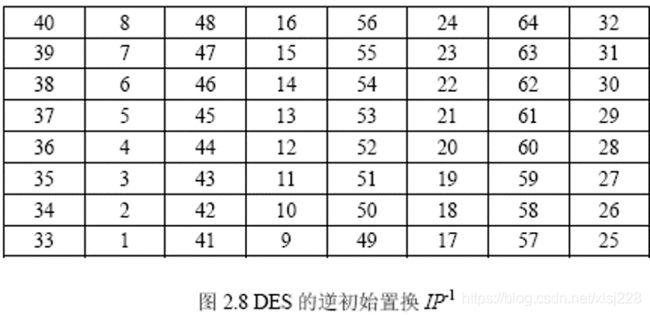
首先对输入的64为明文进行初始置换;

然后进行16次迭代;

最后进行逆置换.

       迭代运算                    初始置换 

（3）迭代运算描述

对置换后的数据X0分为左右两部分，左边L0，右边R0.

对R0进行f变换，结果为f(R0,K1)，得到的32位输出再与L0逐位异或。

异或结果为下一轮R1，原R0变为下一轮L1.

循环16次，最终为R16，L16

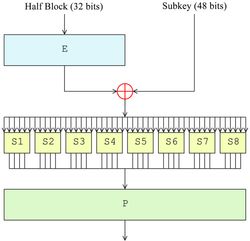
f变换

f函数可以记为f(A,J),其中A是32位输入，J为48位输入。第i轮的A = Ri-1，J = Ki, f(A,J)输出为32位。（k位子密钥）

s变换

将32位的A经过扩展运算变为48位，记作E(A)。与J运算，E(A)⊕J=B，对B实行代换S。此代换由8个盒组成，S-盒。

每个S-盒有6位输入，记作Bi；4位输出，记作Ci。将B分为8组，每组6位：记为b0b1b2b3b4b5b6；取x = b0b5，y=b1b2b3b4；则找到坐标(x,y)=( b0b5, b1b2b3b4)，查找S表，进行压缩运算。

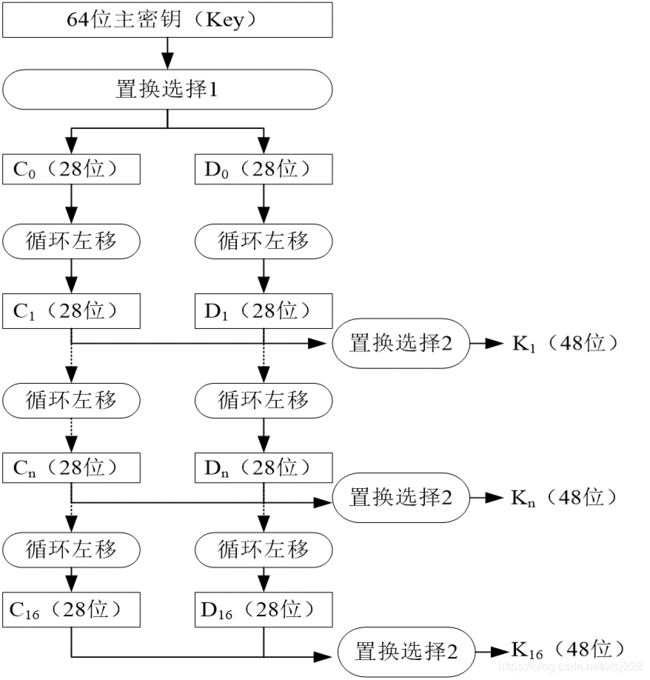
（4）子密钥产生运算

p变换

64位的密钥——剔除8个校验位->56的初始密钥——置换1后分为左右两个28位的，进行左移，置换2操作后又变为48位。

置换1是64变56，置换2是56变48。

工作模式

补充：DES先按64位分组，称为区块，不足64位的叫短块。短块的处理方法：填充法、序列密码加密法、密文挪用技术。

根据加密区块之间的联系方式可以分为：ECB、CBC、CFB、OFB

ECB：基本工作模式，加密区块依次独立加密，互不影响。加密完后再连起来。

CBC：第一个加密区块先于初始向量异或再加密，其他每个加密区块必须与前一个加密区块的密文异或之后再加密。

CFB：流密码加密器一样，按照需要，每次加密的区块大小自定；每个加密区块必须与前一个加密区块的密文异或之后再加密。

OFB：类似CFB，不同的是之前区块加密后的结果为独立产生，不受之前区块的影响。

DES的安全性

(1) DES的密钥长度(56位)可能太短；

(2) DES的迭代次数可能太少；

(3) S-盒中可能有不安全因素；

(4) DES的一些关键部分不应当保密

2）AES

AES的密钥长度可以是128、192、256位三种情况。

AES的输入数据都是128位。

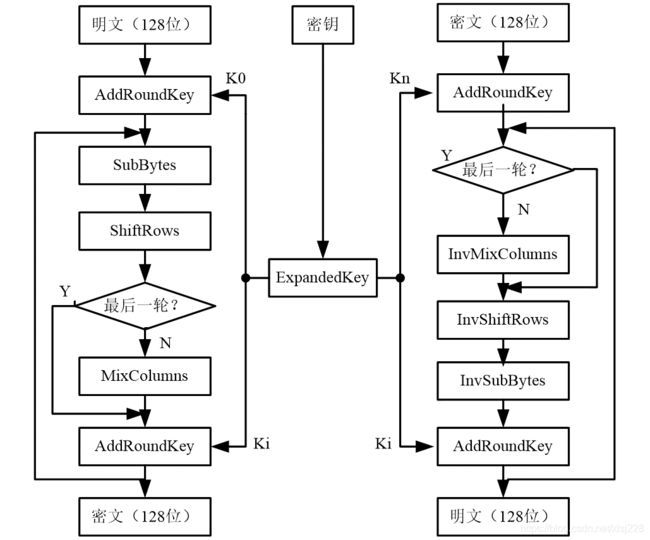
加密解密过程：

首先对明文、密文进行一次密钥加变换，接下来进行多轮循环运算。（循环轮数由密钥长度决定，依次为10、12、14轮）

AES采用替代/置换（SP）网络结构，各轮AES加密循环（除最后一轮外）均包含4个步骤:

(1) 轮密钥加运算(AddRoundKey)

在每次的加密循环中，都会由主密钥产生一把轮密钥，这把密钥大小会跟原矩阵一样，然后与原矩阵中每个对应的字节作异或（⊕）加法。

(2) 字节代换(SubBytes)

矩阵中的各字节通过一个8位的S-box进行转换。S-box与有限域GF(28)上的乘法逆有关。

(3)行位移变换(ShiftRows)

将矩阵中的每个横列进行循环式移位。

(4)列混合变换(MixColumns)

为了充分混合矩阵中各个直行的操作。这个步骤使用线性转换来混合每内联的四个字节。

 3）RSA（*）

加密模型算法描述：

(1) 选择一对不同的、足够大的素数p，q,计算n=pq;

(2）计算Φ(n)=(p-1)(q-1) ;

(3) 找一个与Φ(n)互素的数e，且1

(4) 计算pk，使得pk*sk≡1 mod Φ(n)。

(5) 得到公开密钥KU = {pk,n},私人密钥KP = {sk,n}

RSA算法的安全性完全取决于 P、Q的保密性以及分解大数的难度