Leetcode 01-算法入门与数组-④数组二分查找
LeetCode 01-算法入门与数组-④数组二分查找
一. 二分查找知识
1. 二分查找算法介绍
1.1 二分查找算法简介
二分查找算法(Binary Search Algorithm):也叫做折半查找算法、对数查找算法,是一种用于在有序数组中查找特定元素的高效搜索算法。
二分查找的基本算法思想为:通过确定目标元素所在的区间范围,反复将查找范围减半,直到找到元素或找不到该元素为止。
1.2 二分查找算法步骤
以下是二分查找算法的基本步骤:
-
初始化:首先,确定要查找的有序数据集合。可以是一个数组或列表,确保其中的元素按照升序或者降序排列。
-
确定查找范围:将整个有序数组集合的查找范围确定为整个数组范围区间,即左边界 l e f t left left 和右边界 r i g h t right right。
-
计算中间元素:根据 m i d = ⌊ ( l e f t + r i g h t ) / 2 ⌋ mid = \lfloor (left + right) / 2 \rfloor mid=⌊(left+right)/2⌋ 计算出中间元素下标位置 m i d mid mid。
-
比较中间元素:将目标元素 t a r g e t target target 与中间元素 n u m s [ m i d ] nums[mid] nums[mid] 进行比较:
- 如果 t a r g e t = = n u m s [ m i d ] target == nums[mid] target==nums[mid],说明找到 t a r g e t target target,因此返回中间元素的下标位置 m i d mid mid。
- 如果 t a r g e t < n u m s [ m i d ] target < nums[mid] target<nums[mid],说明目标元素在左半部分( [ l e f t , m i d − 1 ] [left, mid - 1] [left,mid−1]),更新右边界为中间元素的前一个位置,即 r i g h t = m i d − 1 right = mid - 1 right=mid−1。
- 如果 t a r g e t > n u m s [ m i d ] target > nums[mid] target>nums[mid],说明目标元素在右半部分( [ m i d + 1 , r i g h t ] [mid + 1, right] [mid+1,right]),更新左边界为中间元素的后一个位置,即 l e f t = m i d + 1 left = mid + 1 left=mid+1。
-
重复步骤 3 ∼ 4 3 \sim 4 3∼4,直到找到目标元素时返回中间元素下标位置,或者查找范围缩小为空(左边界大于右边界),表示目标元素不存在,此时返回 − 1 -1 −1。
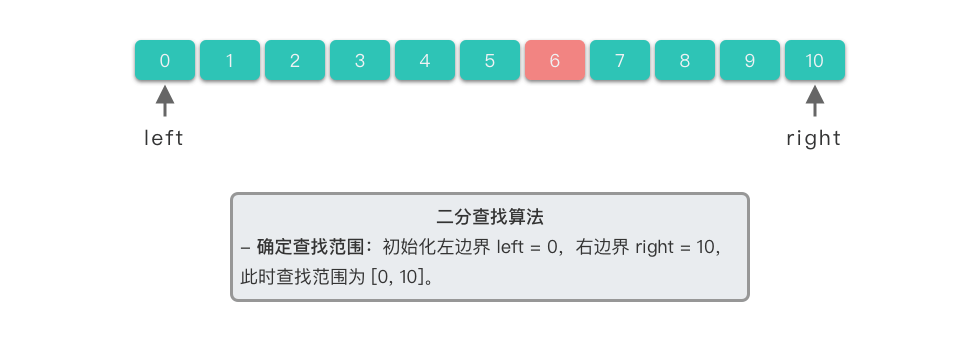
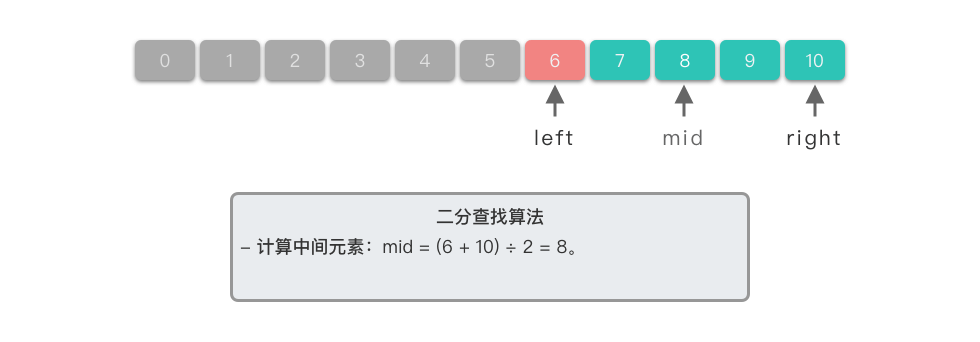
举个例子来说,以在有序数组 [ 0 , 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 , 9 , 10 ] [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10] [0,1,2,3,4,5,6,7,8,9,10] 中查找目标元素 6 6 6 来说,使用二分查找算法的步骤如下:
- 确定查找范围:初始时左边界 l e f t left left 为 0 0 0(数组的起始位置), r i g h t right right 为 10 10 10(数组的末尾位置)。此时查找范围为 [ 0 , 10 ] [0, 10] [0,10]。
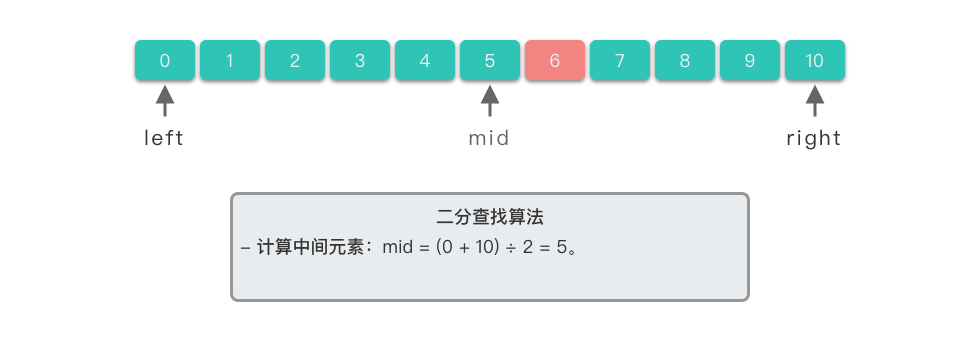
- 计算中间元素:中间元素下标位置为 5 5 5,对应元素为 n u m s [ 5 ] = = 5 nums[5] == 5 nums[5]==5。
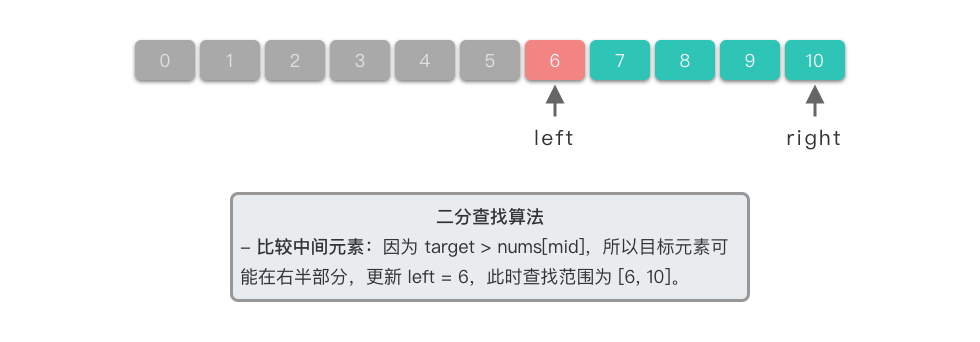
- 比较中间元素:因为 6 > n u m s [ 5 ] 6 > nums[5] 6>nums[5],所以目标元素可能在右半部分,更新左边界为中间元素的后一个位置,即 l e f t = 5 left = 5 left=5。此时查找范围为 [ 5 , 10 ] [5, 10] [5,10]。
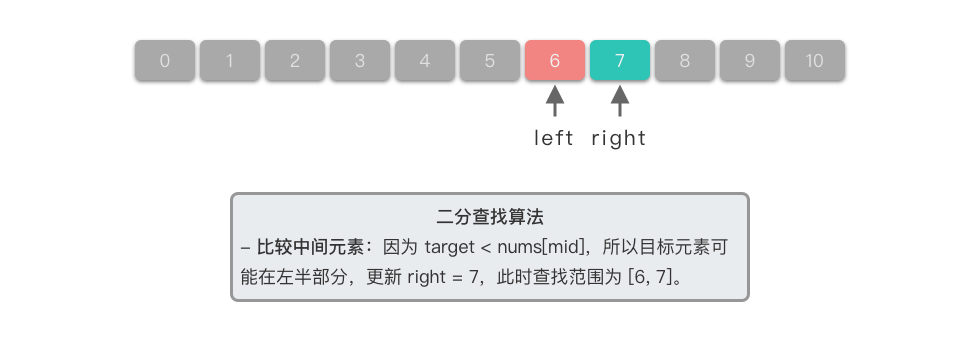
- 计算中间元素:中间元素下标位置为 7 7 7,对应元素为 n u m s [ 7 ] = = 7 nums[7] == 7 nums[7]==7。
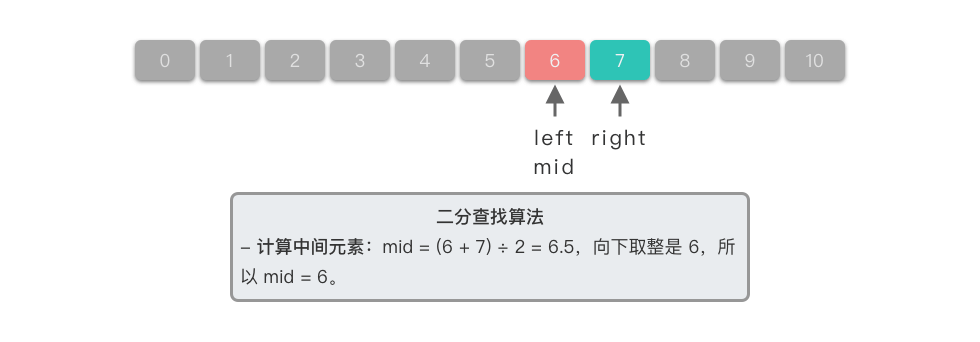
- 比较中间元素:因为 6 < n u m s [ 7 ] 6 < nums[7] 6<nums[7],所以目标元素可能在左半部分,更新右边界为中间元素的前一个位置,即 r i g h t = 6 right = 6 right=6。此时查找范围为 [ 5 , 6 ] [5, 6] [5,6]。
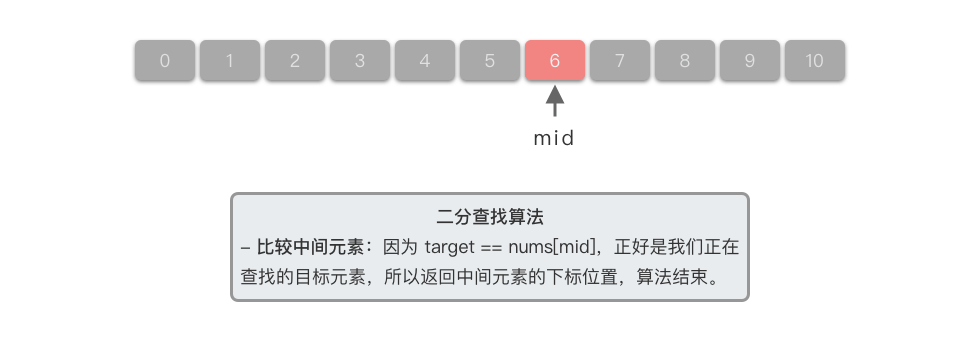
- 计算中间元素:中间元素下标位置为 5 5 5,对应元素为 n u m s [ 5 ] = = 5 nums[5] == 5 nums[5]==5。
- 比较中间元素:因为 5 = = n u m s [ 5 ] 5 == nums[5] 5==nums[5],正好是我们正在查找的目标元素,此时返回中间元素的下标位置,算法结束。
于是我们发现,对于一个长度为 10 10 10 的有序数组,我们只进行了 3 3 3 次查找就找到了目标元素。而如果是按照顺序依次遍历数组,则在最坏情况下,我们可能需要查找 10 10 10 次才能找到目标元素。
<1>
<2>
<3>
<4>
<5>
<6>
<7>
<8>
1.3 二分查找算法思想
二分查找算法是经典的 「减而治之」 的思想。
这里的 「减」 是减少问题规模的意思,「治」 是解决问题的意思。「减」 和 「治」 结合起来的意思就是 「排除法解决问题」。即:每一次查找,排除掉一定不存在目标元素的区间,在剩下可能存在目标元素的区间中继续查找。
每一次通过一些条件判断,将待搜索的区间逐渐缩小,以达到「减少问题规模」的目的。而于问题的规模是有限的,经过有限次的查找,最终会查找到目标元素或者查找失败。
2. 简单二分查找
下面通过一个简单的例子来讲解下二分查找的思路和代码。
- 题目链接:704. 二分查找
2.1 题目大意
描述:给定一个升序的数组 n u m s nums nums,和一个目标值 t a r g e t target target。
要求:返回 t a r g e t target target 在数组中的位置,如果找不到,则返回 − 1 -1 −1。
说明:
- 你可以假设 n u m s nums nums 中的所有元素是不重复的。
- n n n 将在 [ 1 , 10000 ] [1, 10000] [1,10000] 之间。
- n u m s nums nums 的每个元素都将在 [ − 9999 , 9999 ] [-9999, 9999] [−9999,9999]之间。
示例:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
2.2 解题思路
思路 1:二分查找
- 设定左右边界为数组两端,即 l e f t = 0 left = 0 left=0, r i g h t = l e n ( n u m s ) − 1 right = len(nums) - 1 right=len(nums)−1,代表待查找区间为 [ l e f t , r i g h t ] [left, right] [left,right](左闭右闭区间)。
- 取两个节点中心位置 m i d mid mid,先比较中心位置值 n u m s [ m i d ] nums[mid] nums[mid] 与目标值 t a r g e t target target 的大小。
- 如果 t a r g e t = = n u m s [ m i d ] target == nums[mid] target==nums[mid],则返回中心位置。
- 如果 t a r g e t > n u m s [ m i d ] target > nums[mid] target>nums[mid],则将左节点设置为 m i d + 1 mid + 1 mid+1,然后继续在右区间 [ m i d + 1 , r i g h t ] [mid + 1, right] [mid+1,right] 搜索。
- 如果 t a r g e t < n u m s [ m i d ] target < nums[mid] target<nums[mid],则将右节点设置为 m i d − 1 mid - 1 mid−1,然后继续在左区间 [ l e f t , m i d − 1 ] [left, mid - 1] [left,mid−1] 搜索。
- 如果左边界大于右边界,查找范围缩小为空,说明目标元素不存在,此时返回 − 1 -1 −1。
思路 1:代码
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
# 在区间 [left, right] 内查找 target
while left <= right:
# 取区间中间节点
mid = (left + right) // 2
# 如果找到目标值,则直接返回中心位置
if nums[mid] == target:
return mid
# 如果 nums[mid] 小于目标值,则在 [mid + 1, right] 中继续搜索
elif nums[mid] < target:
left = mid + 1
# 如果 nums[mid] 大于目标值,则在 [left, mid - 1] 中继续搜索
else:
right = mid - 1
# 未搜索到元素,返回 -1
return -1
思路 1:复杂度分析
- 时间复杂度: O ( log n ) O(\log n) O(logn)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
3. 二分查找细节
从上篇文章的例子中我们了解了二分查找的思路和具体代码。但是真正在解决二分查找题目的时候还需要考虑更多细节。比如说以下几个问题:
- 区间的开闭问题:区间应该是左闭右闭区间 [ l e f t , r i g h t ] [left, right] [left,right],还是左闭右开区间 [ l e f t , r i g h t ) [left, right) [left,right)?
- m i d mid mid 的取值问题: m i d = ⌊ l e f t + r i g h t 2 ⌋ mid = \lfloor \frac{left + right}{2} \rfloor mid=⌊2left+right⌋,还是 m i d = ⌊ l e f t + r i g h t + 1 2 ⌋ mid = \lfloor \frac{left + right + 1}{2} \rfloor mid=⌊2left+right+1⌋?
- 出界条件的判断: l e f t ≤ r i g h t left \le right left≤right,还是 l e f t < r i g h t left < right left<right?
- 搜索区间范围的选择: l e f t = m i d + 1 left = mid + 1 left=mid+1、 r i g h t = m i d − 1 right = mid - 1 right=mid−1、 l e f t = m i d left = mid left=mid、 r i g h t = m i d right = mid right=mid 应该怎么写?
下面依次进行讲解。
3.1 区间的开闭问题
左闭右闭区间、左闭右开区间指的是初始待查找区间的范围。
-
左闭右闭区间:初始化时, l e f t = 0 left = 0 left=0, r i g h t = l e n ( n u m s ) − 1 right = len(nums) - 1 right=len(nums)−1。
- l e f t left left 为数组第一个元素位置, r i g h t right right 为数组最后一个元素位置。
- 区间 [ l e f t , r i g h t ] [left, right] [left,right] 左右边界上的点都能取到。
-
左闭右开区间:初始化时, l e f t = 0 left = 0 left=0, r i g h t = l e n ( n u m s ) right = len(nums) right=len(nums)。
- l e f t left left 为数组第一个元素位置, r i g h t right right 为数组最后一个元素的下一个位置。
- 区间 [ l e f t , r i g h t ) [left, right) [left,right) 左边界点能取到,而右边界上的点不能取到。
关于二分查找算法的左闭右闭区间、左闭右开区间,其实在网上都有对应的代码。但是相对来说,左闭右开区间这种写法在解决问题的过程中,会使得问题变得复杂,需要考虑的情况更多,所以不建议使用左闭右开区间这种写法,而是建议:全部使用「左闭右闭区间」这种写法。
3.2 m i d mid mid 的取值问题
在二分查找的实际问题中,最常见的 m i d mid mid 取值公式有两个:
mid = (left + right) // 2。mid = (left + right + 1) // 2。
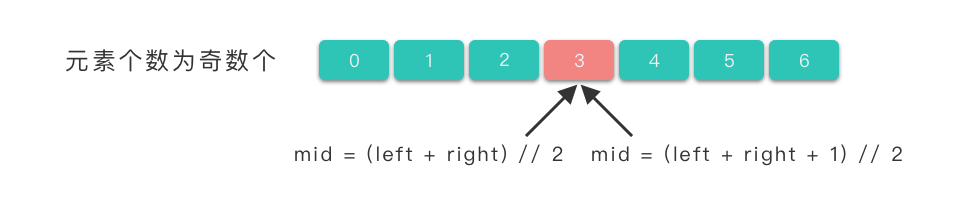
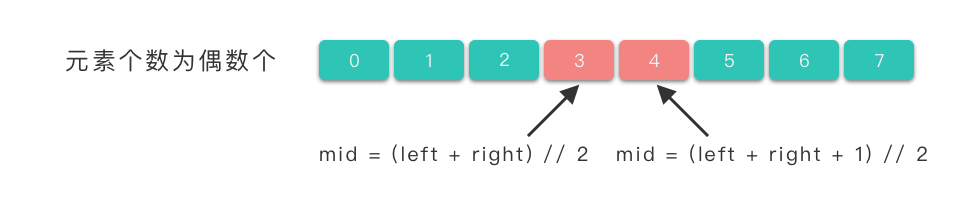
式子中 // 所代表的含义是「中间数向下取整」。当待查找区间中的元素个数为奇数个,使用这两种取值公式都能取到中间元素的下标位置。
而当待查找区间中的元素个数为偶数时,使用 mid = (left + right) // 2 式子我们能取到中间靠左边元素的下标位置,使用 mid = (left + right + 1) // 2 式子我们能取到中间靠右边元素的下标位置。
<1>
<2>
把这两个公式分别代入到 704. 二分查找 的代码中试一试,发现都能通过题目评测。这是为什么呢?
因为二分查找算法的思路是:根据每次选择中间位置上的数值来决定下一次在哪个区间查找元素。每一次选择的元素位置可以是中间位置,但并不是一定非得是区间中间位置元素,靠左一些、靠右一些、甚至区间三分之一、五分之一处等等,都是可以的。比如说 mid = (left + right) * 1 // 5 也是可以的。
但一般来说,取区间中间位置在平均意义下所达到的效果最好。同时这样写最简单。而对于这两个取值公式,大多数时候是选择第一个公式。不过,有些情况下,是需要考虑第二个公式的,我们会在「4.2 排除法」中进行讲解。
除了上面提到的这两种写法,我们还经常能看到下面两个公式:
mid = left + (right - left) // 2。mid = left + (right - left + 1) // 2。
这两个公式其实分别等同于之前两个公式,可以看做是之前两个公式的另一种写法。这种写法能够防止整型溢出问题(Python 语言中整型不会溢出,其他语言可能会有整型溢出问题)。
在 l e f t + r i g h t left + right left+right 的数据量不会超过整型变量最大值时,这两种写法都没有问题。在 l e f t + r i g h t left + right left+right 的数据量可能会超过整型变量最大值时,最好使用第二种写法。所以,为了统一和简化二分查找算法的写法,建议统一写成第二种写法:
mid = left + (right - left) // 2。mid = left + (right - left + 1) // 2。
3.3 出界条件的判断
二分查找算法的写法中,while 语句出界判断条件通常有两种:
left <= right。left < right。
我们究竟应该使用哪一种写法呢?
我们先来判断一下导致 while 语句出界的条件是什么。
- 如果判断语句为
left <= right,并且查找的元素不在有序数组中,则while语句的出界条件是left > right,也就是left == right + 1,写成区间形式就是 [ r i g h t + 1 , r i g h t ] [right + 1, right] [right+1,right],此时待查找区间为空,待查找区间中没有元素存在,此时终止循环时,可以直接返回 − 1 -1 −1。- 比如说区间 [ 3 , 2 ] [3, 2] [3,2], 此时左边界大于右边界,直接终止循环,返回 − 1 -1 −1 即可。
- 如果判断语句为
left < right,并且查找的元素不在有序数组中,则while语句出界条件是left == right,写成区间形式就是 [ r i g h t , r i g h t ] [right, right] [right,right]。此时区间不为空,待查找区间还有一个元素存在,我们并不能确定查找的元素不在这个区间中,此时终止循环时,如果直接返回 − 1 -1 −1 就是错误的。- 比如说区间 [ 2 , 2 ] [2, 2] [2,2],如果元素 n u m s [ 2 ] nums[2] nums[2] 刚好就是目标元素 t a r g e t target target,此时终止循环,返回 − 1 -1 −1 就漏掉了这个元素。
但是如果我们还是想要使用 left < right 的话,怎么办?
可以在出界之后增加一层判断,判断 l e f t left left 所指向位置是否等于目标元素,如果是的话就返回 l e f t left left,如果不是的话返回 − 1 -1 −1。即:
# ...
while left < right:
# ...
return left if nums[left] == target else -1
此外,while 判断语句用 left < right 有一个好处,就是在跳出循环的时候,一定是 left == right,我们就不用判断此时应该返回 l e f t left left 还是 r i g h t right right 了。
3.4 搜索区间范围的选择
在进行区间范围选择的时候,通常有三种写法:
left = mid + 1,right = mid - 1。left = mid + 1,right = mid。left = mid,right = mid - 1。
我们到底应该如何确定搜索区间范围呢?
这是二分查找的一个难点,写错了很容易造成死循环,或者得不到正确结果。
这其实跟二分查找算法的两种不同思路和三种写法有关。
- 思路 1:「直接法」—— 在循环体中找到元素后直接返回结果。
- 思路 2:「排除法」—— 在循环体中排除目标元素一定不存在区间。
接下来我们具体讲解下这两种思路。
4. 二分查找两种思路
4.1 直接法
直接法思想:一旦我们在循环体中找到元素就直接返回结果。
这种思路比较简单,其实我们在上篇 「2. 简单二分查找 - 704. 二分查找」 中就已经用过了。这里再看一下思路和代码:
思路 1:直接法
- 设定左右边界为数组两端,即 l e f t = 0 left = 0 left=0, r i g h t = l e n ( n u m s ) − 1 right = len(nums) - 1 right=len(nums)−1,代表待查找区间为 [ l e f t , r i g h t ] [left, right] [left,right](左闭右闭区间)。
- 取两个节点中心位置 m i d mid mid,先比较中心位置值 n u m s [ m i d ] nums[mid] nums[mid] 与目标值 t a r g e t target target 的大小。
- 如果 t a r g e t = = n u m s [ m i d ] target == nums[mid] target==nums[mid],则返回中心位置。
- 如果 t a r g e t > n u m s [ m i d ] target > nums[mid] target>nums[mid],则将左节点设置为 m i d + 1 mid + 1 mid+1,然后继续在右区间 [ m i d + 1 , r i g h t ] [mid + 1, right] [mid+1,right] 搜索。
- 如果 t a r g e t < n u m s [ m i d ] target < nums[mid] target<nums[mid],则将右节点设置为 m i d − 1 mid - 1 mid−1,然后继续在左区间 [ l e f t , m i d − 1 ] [left, mid - 1] [left,mid−1] 搜索。
- 如果左边界大于右边界,查找范围缩小为空,说明目标元素不存在,此时返回 − 1 -1 −1。
思路 1:代码
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
# 在区间 [left, right] 内查找 target
while left <= right:
# 取区间中间节点
mid = left + (right - left) // 2
# 如果找到目标值,则直接范围中心位置
if nums[mid] == target:
return mid
# 如果 nums[mid] 小于目标值,则在 [mid + 1, right] 中继续搜索
elif nums[mid] < target:
left = mid + 1
# 如果 nums[mid] 大于目标值,则在 [left, mid - 1] 中继续搜索
else:
right = mid - 1
# 未搜索到元素,返回 -1
return -1
思路 1:细节
- 这种思路是在一旦循环体中找到元素就直接返回。
- 循环可以继续的条件是
left <= right。 - 如果一旦退出循环,则说明这个区间内一定不存在目标元素。
4.2 排除法
排除法思想:在循环体中排除目标元素一定不存在区间。
思路 2:排除法
- 设定左右边界为数组两端,即 l e f t = 0 left = 0 left=0, r i g h t = l e n ( n u m s ) − 1 right = len(nums) - 1 right=len(nums)−1,代表待查找区间为 [ l e f t , r i g h t ] [left, right] [left,right](左闭右闭区间)。
- 取两个节点中心位置 m i d mid mid,比较目标元素和中间元素的大小,先将目标元素一定不存在的区间排除。
- 然后在剩余区间继续查找元素,继续根据条件排除目标元素一定不存在的区间。
- 直到区间中只剩下最后一个元素,然后再判断这个元素是否是目标元素。
根据排除法的思路,我们可以写出来两种代码。
思路 2:代码 1
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
# 在区间 [left, right] 内查找 target
while left < right:
# 取区间中间节点
mid = left + (right - left) // 2
# nums[mid] 小于目标值,排除掉不可能区间 [left, mid],在 [mid + 1, right] 中继续搜索
if nums[mid] < target:
left = mid + 1
# nums[mid] 大于等于目标值,目标元素可能在 [left, mid] 中,在 [left, mid] 中继续搜索
else:
right = mid
# 判断区间剩余元素是否为目标元素,不是则返回 -1
return left if nums[left] == target else -1
思路 2:代码 2
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
# 在区间 [left, right] 内查找 target
while left < right:
# 取区间中间节点
mid = left + (right - left + 1) // 2
# nums[mid] 大于目标值,排除掉不可能区间 [mid, right],在 [left, mid - 1] 中继续搜索
if nums[mid] > target:
right = mid - 1
# nums[mid] 小于等于目标值,目标元素可能在 [mid, right] 中,在 [mid, right] 中继续搜索
else:
left = mid
# 判断区间剩余元素是否为目标元素,不是则返回 -1
return left if nums[left] == target else -1
思路 2:细节
-
判断语句是
left < right。这样在退出循环时,一定有left == right成立,就不用判断应该返回 l e f t left left 还是 r i g h t right right 了。此时只需要判断 n u m s [ l e f t ] nums[left] nums[left] 是否为目标元素即可。 -
在循环体中,比较目标元素和中间元素的大小之后,优先将目标元素一定不存在的区间排除,然后再从剩余区间中确定下一次查找区间的范围。
-
在将目标元素一定不存在的区间排除之后,它的对立面(即
else部分)一般就不需要再考虑区间范围了,直接取上一个区间的相反区间。如果上一个区间是 [ m i d + 1 , r i g h t ] [mid + 1, right] [mid+1,right],那么相反区间就是 [ l e f t , m i d ] [left, mid] [left,mid]。如果上一个区间是 [ l e f t , m i d − 1 ] [left, mid - 1] [left,mid−1],那么相反区间就是 [ m i d , r i g h t ] [mid, right] [mid,right]。 -
为了避免陷入死循环,当区分被划分为 [ l e f t , m i d − 1 ] [left, mid - 1] [left,mid−1] 与 [ m i d , r i g h t ] [mid, right] [mid,right] 两部分时, m i d mid mid 取值要向上取整。即
mid = left + (right - left + 1) // 2。因为如果当区间中只剩下两个元素时(此时right = left + 1),一旦进入left = mid分支,区间就不会再缩小了,下一次循环的查找区间还是 [ l e f t , r i g h t ] [left, right] [left,right],就陷入了死循环。- 比如左边界 l e f t = 5 left = 5 left=5,右边界 r i g h t = 6 right = 6 right=6,此时查找区间为 [ 5 , 6 ] [5, 6] [5,6], m i d = 5 + ( 6 − 5 ) / / 2 = 5 mid = 5 + (6 - 5) // 2 = 5 mid=5+(6−5)//2=5,如果进入 l e f t = m i d left = mid left=mid 分支,那么下次查找区间仍为 [ 5 , 6 ] [5, 6] [5,6],区间不再缩小,陷入死循环。
- 这种情况下, m i d mid mid 应该向上取整, m i d = 5 + ( 6 − 5 + 1 ) / / 2 = 6 mid = 5 + (6 - 5 + 1) // 2 = 6 mid=5+(6−5+1)//2=6,如果进入 l e f t = m i d left = mid left=mid 分支,则下次查找区间为 [ 6 , 6 ] [6, 6] [6,6]。
-
关于边界设置可以记忆为:只要看到
left = mid就向上取整。或者记为:left = mid + 1、right = mid和mid = left + (right - left) // 2一定是配对出现的。right = mid - 1、left = mid和mid = left + (right - left + 1) // 2一定是配对出现的。
4.3 两种思路适用范围
- 直接法:因为判断语句是
left <= right,有时候要考虑返回是 l e f t left left 还是 r i g h t right right。循环体内有 3 个分支,并且一定有一个分支用于退出循环或者直接返回。这种思路适合解决简单题目。即要查找的元素性质简单,数组中都是非重复元素,且==、>、<的情况非常好写的时候。 - 排除法:更加符合二分查找算法的减治思想。每次排除目标元素一定不存在的区间,达到减少问题规模的效果。然后在可能存在的区间内继续查找目标元素。这种思路适合解决复杂题目。比如查找一个数组里可能不存在的元素,找边界问题,可以使用这种思路。
参考资料
- 【博文】Learning-Algorithms-with-Leetcode - 第 3.1 节 二分查找算法
- 【博文】二分法的细节加细节 你真的应该搞懂!!!_小马的博客
- 【课程】零起步学算法 - LeetBook - 二分查找的基本思想:减而治之
- 【题解】二分查找算法细节详解,顺便写了首诗 - LeetCode
二. 练习题目
1. 0704. 二分查找
1.1 题目大意
描述:给定一个升序的数组 nums,和一个目标值 target。
要求:返回 target 在数组中的位置,如果找不到,则返回 -1。
说明:
- 你可以假设
nums中的所有元素是不重复的。 n将在[1, 10000]之间。nums的每个元素都将在[-9999, 9999]之间。
示例:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
1.2 解题思路
思路 1:二分查找
设定左右节点为数组两端,即 left = 0,right = len(nums) - 1,代表待查找区间为 [left, right](左闭右闭)。
取两个节点中心位置 mid,先比较中心位置值 nums[mid] 与目标值 target 的大小。
- 如果中心位置值
nums[mid]与目标值target相等,则返回中心位置。 - 如果中心位置值
nums[mid]小于目标值target,则将左节点设置为mid + 1,然后继续在右区间[mid + 1, right]搜索。 - 如果中心位置值
nums[mid]大于目标值target,则将右节点设置为mid - 1,然后继续在左区间[left, mid - 1]搜索。
思路 1:代码
class Solution:
def search(self, nums: List[int], target: int) -> int:
left, right = 0, len(nums) - 1
# 在区间 [left, right] 内查找 target
while left <= right:
# 取区间中间节点
mid = (left + right) // 2
# 如果找到目标值,则直接返回中心位置
if nums[mid] == target:
return mid
# 如果 nums[mid] 小于目标值,则在 [mid + 1, right] 中继续搜索
elif nums[mid] < target:
left = mid + 1
# 如果 nums[mid] 大于目标值,则在 [left, mid - 1] 中继续搜索
else:
right = mid - 1
# 未搜索到元素,返回 -1
return -1
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
2. 0035. 搜索插入位置
2.1 题目大意
描述:给定一个排好序的数组 nums,以及一个目标值 target。
要求:在数组中找到目标值,并返回下标。如果找不到,则返回目标值按顺序插入数组的位置。
说明:
- 1 ≤ n u m s . l e n g t h ≤ 1 0 4 1 \le nums.length \le 10^4 1≤nums.length≤104。
- − 1 0 4 ≤ n u m s [ i ] ≤ 1 0 4 -10^4 \le nums[i] \le 10^4 −104≤nums[i]≤104。
- n u m s nums nums 为无重复元素的升序排列数组。
- − 1 0 4 ≤ t a r g e t ≤ 1 0 4 -10^4 \le target \le 10^4 −104≤target≤104。
示例:
输入:nums = [1,3,5,6], target = 5
输出:2
2.2 解题思路
思路 1:二分查找
设定左右节点为数组两端,即 left = 0,right = len(nums) - 1,代表待查找区间为 [left, right](左闭右闭)。
取两个节点中心位置 mid,先比较中心位置值 nums[mid] 与目标值 target 的大小。
- 如果中心位置值
nums[mid]与目标值target相等,则当前中心位置为待插入数组的位置。 - 如果中心位置值
nums[mid]小于目标值target,则将左节点设置为mid + 1,然后继续在右区间[mid + 1, right]搜索。 - 如果中心位置值
nums[mid]大于目标值target,则将右节点设置为mid - 1,然后继续在左区间[left, mid - 1]搜索。
直到查找到目标值返回待插入数组的位置,或者等到 left > right 时停止查找,此时 left 所在位置就是待插入数组的位置。
思路 1:二分查找代码
class Solution:
def searchInsert(self, nums: List[int], target: int) -> int:
size = len(nums)
left, right = 0, size - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
elif nums[mid] < target:
left = mid + 1
else:
right = mid - 1
return left
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2 n) O(log2n)。二分查找算法的时间复杂度为 O ( log 2 n ) O(\log_2 n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
3. 0374. 猜数字大小
3.1 题目大意
描述:猜数字游戏。给定一个整数 n 和一个接口 def guess(num: int) -> int:,题目会从 1 ~ n 中随机选取一个数 x。我们只能通过调用接口来判断自己猜测的数是否正确。
要求:要求返回题目选取的数字 x。
说明:
def guess(num: int) -> int:返回值:- − 1 -1 −1:我选出的数字比你猜的数字小,即 p i c k < n u m pick < num pick<num;
- 1 1 1:我选出的数字比你猜的数字大 p i c k > n u m pick > num pick>num;
- 0 0 0:我选出的数字和你猜的数字一样。恭喜!你猜对了! p i c k = = n u m pick == num pick==num。
示例:
输入:n = 10, pick = 6
输出:6
3.2 解题思路
思路 1:二分查找
利用两个指针 left、right。left 指向数字 1,right 指向数字 n。每次从中间开始调用接口猜测是否正确。
- 如果猜测的数比选中的数大,则将
right向左移,令right = mid - 1,继续从中间调用接口猜测; - 如果猜测的数比选中的数小,则将
left向右移,令left = mid + 1,继续从中间调用的接口猜测; - 如果猜测正确,则直接返回该数。
思路 1:二分查找代码
class Solution:
def guessNumber(self, n: int) -> int:
left = 1
right = n
while left <= right:
mid = left + (right - left) // 2
ans = guess(mid)
if ans == 1:
left = mid + 1
elif ans == -1:
right = mid - 1
else:
return mid
return 0
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2 n) O(log2n)。二分查找算法的时间复杂度为 O ( log 2 n ) O(\log_2 n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
4. 0069. x 的平方根
4.1 题目大意
要求:实现 int sqrt(int x) 函数。计算并返回 x 的平方根(只保留整数部分),其中 x 是非负整数。
说明:
- 0 ≤ x ≤ 2 31 − 1 0 \le x \le 2^{31} - 1 0≤x≤231−1。
示例:
输入:x = 4
输出:2
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
4.2 解题思路
思路 1:二分查找
因为求解的是 x 开方的整数部分。所以我们可以从 0 ~ x 的范围进行遍历,找到 k 2 ≤ x k^2 \le x k2≤x 的最大结果。
为了减少算法的时间复杂度,我们使用二分查找的方法来搜索答案。
思路 1:代码
class Solution:
def mySqrt(self, x: int) -> int:
left = 0
right = x
ans = -1
while left <= right:
mid = (left + right) // 2
if mid * mid <= x:
ans = mid
left = mid + 1
else:
right = mid - 1
return ans
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2 n) O(log2n)。二分查找算法的时间复杂度为 O ( log 2 n ) O(\log_2 n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
5. 0167. 两数之和 II - 输入有序数组
5.1 题目大意
描述:给定一个下标从 1 开始计数、升序排列的整数数组:numbers 和一个目标值 target。
要求:从数组中找出满足相加之和等于 target 的两个数,并返回两个数在数组中下的标值。
说明:
- 2 ≤ n u m b e r s . l e n g t h ≤ 3 ∗ 1 0 4 2 \le numbers.length \le 3 * 10^4 2≤numbers.length≤3∗104。
- − 1000 ≤ n u m b e r s [ i ] ≤ 1000 -1000 \le numbers[i] \le 1000 −1000≤numbers[i]≤1000。
- n u m b e r s numbers numbers 按非递减顺序排列。
- − 1000 ≤ t a r g e t ≤ 1000 -1000 \le target \le 1000 −1000≤target≤1000。
- 仅存在一个有效答案。
示例:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
5.2 解题思路
思路 1:双指针
可以考虑使用双指针来减少时间复杂度。具体做法如下:
- 使用两个指针
left,right。left指向数组第一个值最小的元素位置,right指向数组值最大元素位置。 - 判断两个位置上的元素的和与目标值的关系。
- 如果元素和等于目标值,则返回两个元素位置。
- 如果元素和大于目标值,则让
right左移,继续检测。 - 如果元素和小于目标值,则让
left右移,继续检测。
- 直到
left和right移动到相同位置停止检测。 - 如果最终仍没找到,则返回
[-1, -1]。
思路 1:代码
class Solution:
def twoSum(self, numbers: List[int], target: int) -> List[int]:
left = 0
right = len(numbers) - 1
while left < right:
total = numbers[left] + numbers[right]
if total == target:
return [left + 1, right + 1]
elif total < target:
left += 1
else:
right -= 1
return [-1, -1]
思路 1:复杂度分析
- 时间复杂度: O ( n ) O(n) O(n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
6. 1011. 在 D 天内送达包裹的能力
6.1 题目大意
描述:传送带上的包裹必须在 D 天内从一个港口运送到另一个港口。给定所有包裹的重量数组 weights,货物必须按照给定的顺序装运。且每天船上装载的重量不会超过船的最大运载重量。
要求:求能在 D 天内将所有包裹送达的船的最低运载量。
说明:
- 1 ≤ d a y s ≤ w e i g h t s . l e n g t h ≤ 5 ∗ 1 0 4 1 \le days \le weights.length \le 5 * 10^4 1≤days≤weights.length≤5∗104。
- 1 ≤ w e i g h t s [ i ] ≤ 500 1 \le weights[i] \le 500 1≤weights[i]≤500。
示例:
输入:weights = [1,2,3,4,5,6,7,8,9,10], days = 5
输出:15
解释:
船舶最低载重 15 就能够在 5 天内送达所有包裹,如下所示:
第 1 天:1, 2, 3, 4, 5
第 2 天:6, 7
第 3 天:8
第 4 天:9
第 5 天:10
请注意,货物必须按照给定的顺序装运,因此使用载重能力为 14 的船舶并将包装分成 (2, 3, 4, 5), (1, 6, 7), (8), (9), (10) 是不允许的。
输入:weights = [3,2,2,4,1,4], days = 3
输出:6
解释:
船舶最低载重 6 就能够在 3 天内送达所有包裹,如下所示:
第 1 天:3, 2
第 2 天:2, 4
第 3 天:1, 4
6.2 解题思路
思路 1:二分查找
船最小的运载能力,最少也要等于或大于最重的那件包裹,即 max(weights)。最多的话,可以一次性将所有包裹运完,即 sum(weights)。船的运载能力介于 [max(weights), sum(weights)] 之间。
我们现在要做的就是从这个区间内,找到满足可以在 D 天内运送完所有包裹的最小载重量。
可以通过二分查找的方式,找到满足要求的最小载重量。
思路 1:代码
class Solution:
def shipWithinDays(self, weights: List[int], D: int) -> int:
left = max(weights)
right = sum(weights)
while left < right:
mid = (left + right) >> 1
days = 1
cur = 0
for weight in weights:
if cur + weight > mid:
days += 1
cur = 0
cur += weight
if days <= D:
right = mid
else:
left = mid + 1
return left
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2 n) O(log2n)。二分查找算法的时间复杂度为 O ( log 2 n ) O(\log_2 n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
7. 0278. 第一个错误的版本
7.1 题目大意
描述:给你一个整数 n,代表已经发布的版本号。还有一个用于检测版本是否出错的接口 isBadVersion(version): 。
要求:找出第一次出错的版本号 bad。
说明:
- 要求尽可能减少对
isBadVersion(version):接口的调用。 - 1 ≤ b a d ≤ n ≤ 2 31 − 1 1 \le bad \le n \le 2^{31} - 1 1≤bad≤n≤231−1。
示例:
输入:n = 5, bad = 4
输出:4
解释:
调用 isBadVersion(3) -> false
调用 isBadVersion(5) -> true
调用 isBadVersion(4) -> true
所以,4 是第一个错误的版本。
输入:n = 1, bad = 1
输出:1
7.2 解题思路
思路 1:二分查找
题目要求尽可能减少对 isBadVersion(version): 接口的调用,所以不能对每个版本都调用接口,而是应该将接口调用的次数降到最低。
可以注意到:如果检测某个版本不是错误版本时,则该版本之前的所有版本都不是错误版本。而当某个版本是错误版本时,则该版本之后的所有版本都是错误版本。我们可以利用这样的性质,在 [1, n] 的区间内使用二分查找方法,从而在 O ( log 2 n ) O(\log_2n) O(log2n) 次内找到第一个出错误的版本。
思路 1:代码
class Solution:
def firstBadVersion(self, n):
left = 1
right = n
while left < right:
mid = (left + right) // 2
if isBadVersion(mid):
right = mid
else:
left = mid + 1
return left
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2 n) O(log2n)。二分查找算法的时间复杂度为 O ( log 2 n ) O(\log_2 n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
8. 0033. 搜索旋转排序数组
8.1 题目大意
描述:给定一个整数数组 nums,数组中值互不相同。给定的 nums 是经过升序排列后的又进行了「旋转」操作的。再给定一个整数 target。
要求:从 nums 中找到 target 所在位置,如果找到,则返回对应下标,找不到则返回 -1。
说明:
- 旋转操作:升序排列的数组 nums 在预先未知的第 k 个位置进行了右移操作,变成了
[nums[k]], nums[k+1], ... , nums[n-1], ... , nums[0], nums[1], ... , nums[k-1]。
示例:
输入:nums = [4,5,6,7,0,1,2], target = 0
输出:4
输入:nums = [4,5,6,7,0,1,2], target = 3
输出:-1
8.2 解题思路
思路 1:二分查找
原本为升序排列的数组 nums 经过「旋转」之后,会有两种情况,第一种就是原先的升序序列,另一种是两段升序的序列。
*
*
*
*
*
*
*
*
*
*
*
*
最直接的办法就是遍历一遍,找到目标值 target。但是还可以有更好的方法。考虑用二分查找来降低算法的时间复杂度。
我们将旋转后的数组看成左右两个升序部分:左半部分和右半部分。
有人会说第一种情况不是只有一个部分吗?其实我们可以把第一种情况中的整个数组看做是左半部分,然后右半部分为空数组。
然后创建两个指针 left、right,分别指向数组首尾。让后计算出两个指针中间值 mid。将 mid 与两个指针做比较,并考虑与 target 的关系。
-
如果
mid[mid] == target,说明找到了target,直接返回下标。 -
如果
nums[mid] ≥ nums[left],则mid在左半部分(因为右半部分值都比nums[left]小)。- 如果
nums[mid] ≥ target,并且target ≥ nums[left],则target在左半部分,并且在mid左侧,此时应将right左移到mid - 1位置。 - 否则如果
nums[mid] ≤ target,则target在左半部分,并且在mid右侧,此时应将left右移到mid + 1位置。 - 否则如果
nums[left] > target,则target在右半部分,应将left移动到mid + 1位置。
- 如果
-
如果
nums[mid] < nums[left],则mid在右半部分(因为右半部分值都比nums[left]小)。- 如果
nums[mid] < target,并且target ≤ nums[right],则target在右半部分,并且在mid右侧,此时应将left右移到mid + 1位置。 - 否则如果
nums[mid] ≥ target,则target在右半部分,并且在mid左侧,此时应将right左移到mid - 1位置。 - 否则如果
nums[right] < target,则target在左半部分,应将right左移到mid - 1位置。
- 如果
思路 1:代码
class Solution:
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] == target:
return mid
if nums[mid] >= nums[left]:
if nums[mid] > target and target >= nums[left]:
right = mid - 1
else:
left = mid + 1
else:
if nums[mid] < target and target <= nums[right]:
left = mid + 1
else:
right = mid - 1
return -1
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2 n) O(log2n)。二分查找算法的时间复杂度为 O ( log 2 n ) O(\log_2 n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
9. 0153. 寻找旋转排序数组中的最小值
9.1 题目大意
描述:给定一个数组 nums,nums 是有升序数组经过「旋转」得到的。但是旋转次数未知。数组中不存在重复元素。
要求:找出数组中的最小元素。
说明:
- 旋转操作:将数组整体右移若干位置。
- n = = n u m s . l e n g t h n == nums.length n==nums.length。
- 1 ≤ n ≤ 5000 1 \le n \le 5000 1≤n≤5000。
- − 5000 ≤ n u m s [ i ] ≤ 5000 -5000 \le nums[i] \le 5000 −5000≤nums[i]≤5000。
- n u m s nums nums 中的所有整数互不相同。
- n u m s nums nums 原来是一个升序排序的数组,并进行了 1 1 1 至 n n n 次旋转。
示例:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
9.2 解题思路
思路 1:二分查找
数组经过「旋转」之后,会有两种情况,第一种就是原先的升序序列,另一种是两段升序的序列。
第一种的最小值在最左边。第二种最小值在第二段升序序列的第一个元素。
*
*
*
*
*
*
*
*
*
*
*
*
最直接的办法就是遍历一遍,找到最小值。但是还可以有更好的方法。考虑用二分查找来降低算法的时间复杂度。
创建两个指针 left、right,分别指向数组首尾。让后计算出两个指针中间值 mid。将 mid 与两个指针做比较。
- 如果
nums[mid] > nums[right],则最小值不可能在mid左侧,一定在mid右侧,则将left移动到mid + 1位置,继续查找右侧区间。 - 如果
nums[mid] ≤ nums[right],则最小值一定在mid左侧,或者mid位置,将right移动到mid位置上,继续查找左侧区间。
思路 1:代码
class Solution:
def findMin(self, nums: List[int]) -> int:
left = 0
right = len(nums) - 1
while left < right:
mid = left + (right - left) // 2
if nums[mid] > nums[right]:
left = mid + 1
else:
right = mid
return nums[left]
思路 1:复杂度分析
- 时间复杂度: O ( log 2 n ) O(\log_2 n) O(log2n)。二分查找算法的时间复杂度为 O ( log 2 n ) O(\log_2 n) O(log2n)。
- 空间复杂度: O ( 1 ) O(1) O(1)。只用到了常数空间存放若干变量。
三. 二分查找题目
1. 二分下标题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0704 | 二分查找 | 网页链接、Github 链接 | 数组、二分查找 | 简单 |
| 0374 | 猜数字大小 | 网页链接、Github 链接 | 二分查找、交互 | 简单 |
| 0035 | 搜索插入位置 | 网页链接、Github 链接 | 数组、二分查找 | 简单 |
| 0034 | 在排序数组中查找元素的第一个和最后一个位置 | 网页链接、Github 链接 | 数组、二分查找 | 中等 |
| 0167 | 两数之和 II - 输入有序数组 | 网页链接、Github 链接 | 数组、双指针、二分查找 | 中等 |
| 0153 | 寻找旋转排序数组中的最小值 | 网页链接、Github 链接 | 数组、二分查找 | 中等 |
| 0154 | 寻找旋转排序数组中的最小值 II | 数组、二分查找 | 困难 | |
| 0033 | 搜索旋转排序数组 | 网页链接、Github 链接 | 数组、二分查找 | 中等 |
| 0081 | 搜索旋转排序数组 II | 数组、二分查找 | 中等 | |
| 0278 | 第一个错误的版本 | 网页链接、Github 链接 | 二分查找、交互 | 简单 |
| 0162 | 寻找峰值 | 网页链接、Github 链接 | 数组、二分查找 | 中等 |
| 0852 | 山脉数组的峰顶索引 | 数组、二分查找 | 中等 | |
| 1095 | 山脉数组中查找目标值 | 数组、二分查找、交互 | 困难 | |
| 0744 | 寻找比目标字母大的最小字母 | 数组、二分查找 | 简单 | |
| 0004 | 寻找两个正序数组的中位数 | 数组、二分查找、分治 | 困难 | |
| 0074 | 搜索二维矩阵 | 数组、二分查找、矩阵 | 中等 | |
| 0240 | 搜索二维矩阵 II | 数组、二分查找、分治、矩阵 | 中等 |
2. 二分答案题目
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0069 | x 的平方根 | 网页链接、Github 链接 | 数学、二分查找 | 简单 |
| 0287 | 寻找重复数 | 位运算、数组、双指针、二分查找 | 中等 | |
| 0050 | Pow(x, n) | 网页链接、Github 链接 | 递归、数学 | 中等 |
| 0367 | 有效的完全平方数 | 数学、二分查找 | 简单 | |
| 1300 | 转变数组后最接近目标值的数组和 | 数组、二分查找、排序 | 中等 | |
| 0400 | 第 N 位数字 | 数学、二分查找 | 中等 |
3. 复杂的二分查找问题
| 题号 | 标题 | 题解 | 标签 | 难度 |
|---|---|---|---|---|
| 0875 | 爱吃香蕉的珂珂 | 数组、二分查找 | 中等 | |
| 0410 | 分割数组的最大值 | 贪心、数组、二分查找、动态规划、前缀和 | 困难 | |
| 0209 | 长度最小的子数组 | 网页链接、Github 链接 | 数组、二分查找、前缀和、滑动窗口 | 中等 |
| 0658 | 找到 K 个最接近的元素 | 数组、双指针、二分查找、排序、滑动窗口、堆(优先队列) | 中等 | |
| 0270 | 最接近的二叉搜索树值 | 树、深度优先搜索、二叉搜索树、二分查找、二叉树 | 简单 | |
| 0702 | 搜索长度未知的有序数组 | 数组、二分查找、交互 | 中等 | |
| 0349 | 两个数组的交集 | 网页链接、Github 链接 | 数组、哈希表、双指针、二分查找、排序 | 简单 |
| 0350 | 两个数组的交集 II | 数组、哈希表、双指针、二分查找、排序 | 简单 | |
| 0287 | 寻找重复数 | 位运算、数组、双指针、二分查找 | 中等 | |
| 0719 | 找出第 K 小的数对距离 | 数组、双指针、二分查找、排序 | 困难 | |
| 0259 | 较小的三数之和 | 数组、双指针、二分查找、排序 | 中等 | |
| 1011 | 在 D 天内送达包裹的能力 | 数组、二分查找 | 中等 | |
| 1482 | 制作 m 束花所需的最少天数 | 数组、二分查找 | 中等 |