C++ - AVL树实现(下篇)- 调试小技巧
前言
本博客是 AVL树的下篇,上篇请看:C++ - AVL 树 介绍 和 实现 (上篇)_chihiro1122的博客-CSDN博客
上篇当中写插入操作,和其中涉及的 旋转等等细节,还有AVL树的大体框架。
调试小技巧
条件断点
在大项目当中,如果发生了程序的错误,崩溃的异常情况,那么因为项目过大,很多时候我们不能一步步去调试,这样非常的麻烦而且不现实。
在VS studio 当中,除了支持逐语句调试之外,还支持 条件调试,就是在某一个断点处,写上一句条件判别式,也就是表达式,可以设置当中这个 表达式为 false 或者 true 的时候,在此处语句停下来:
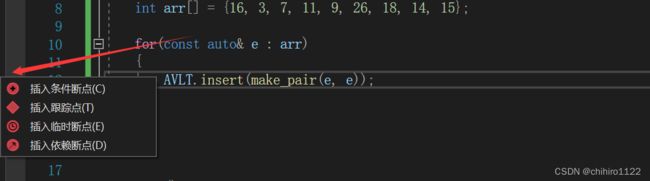
当我们右键做左边一列的(断点列),就会出现下图当中的 内容:
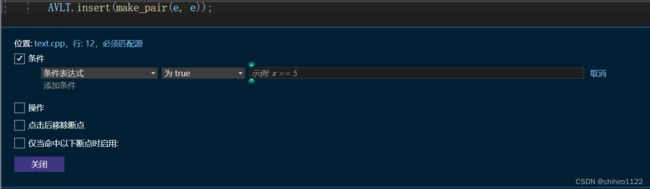
此时就会出现上述内容,上述内容就是 条件断点当中的条件设置,你可以在 最右边(在示例:x== 5 ) 这个位置处,写上你需要的条件表达式,然后还可以设置这个表达式为 true 或者为 false的时候停止执行。注意:是程序执行到 该断点处,才会进行判断表达式真假,才会进行停止或者继续执行的操作。
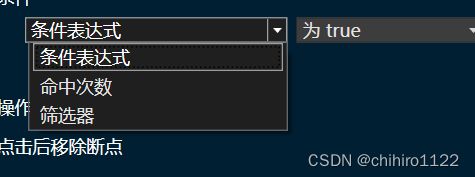
当然,此处不仅可以加条件表达式判断,还可以加一些 其他 判断方式:
可以自己下去研究。
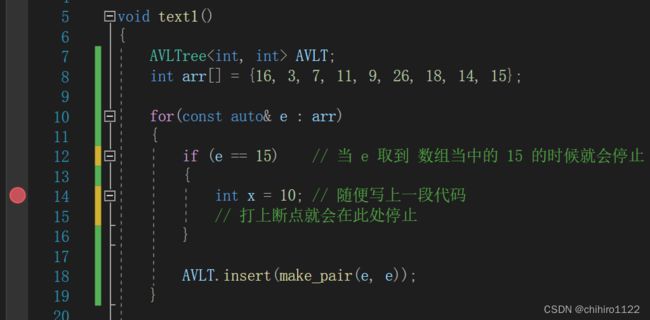
其实还有一个方法和上述方法类似,我们可以在我们想要打断的地方,自己写一个 if()判断语句,然后在其中随便写上一段代码,打上断点,也可以实现和上述一眼的操作;注意:一定要在if()当中写上一行代码,空行是不能打断点的,会直接跳过:
如上所示,当 e 遍历的到 数组的 15 的时候,到达 if()就会停止。
这样,按下 f5 就会 执行到 e 遍历到 数组 15 这个元素之后停止,就不用再 手动调试到 15 这个元素位置了。
如果 这颗数非常大的话,那么上述方式还是非常好用的,加入在 15之前有 200 个需要插入的元素,手动一步步调试到 15 肯定是不现实的。
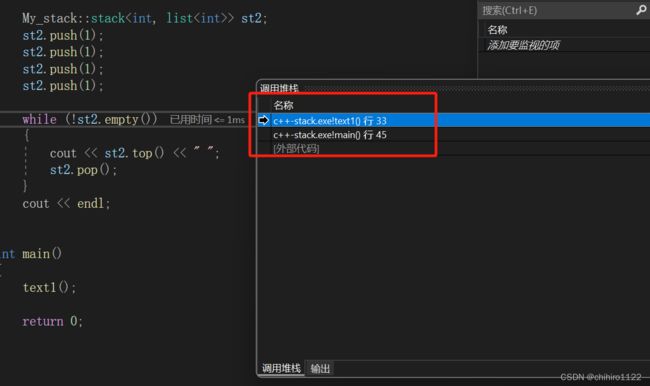
调用堆栈
可以在调试->窗口当中找到 调用堆栈这个窗口,当我们逐语句查看代码执行过程的时候,其中可能会调用多个函数,而每一个函数都有对应的函数栈帧,如果单独使用 f10 f11 来走的话,不好回溯;这时候我们可以在 调用堆栈这个窗口当中看到 从开始到现在,所调用函数的函数堆栈:
此时我们只需要点击一下其中某一个函数堆栈,就可以直接回溯到 这个函数当中进行执行。
写一些小程序来帮助我们判别一些规律性问题
比如在自己实现 AVL 树当中,我们不太可能一步就直接写到位,出错是大概率的事情,而且像AVL树这种规则复杂的数据结构,在调试起非常的麻烦,此时我们为了更好的调试,写一个小程序来帮助我们判断,每插入一个结点之后,这颗树还是不是一颗 AVL树。
AVL树
判断一颗AVL树是不是 平衡的
private:
int Height(Node* root)
{
if (root == nullptr)
return 0;
int HeightLeft = Height(root->_left);
int HeightRight = Height(root->_right);
return HeightLeft > HeightRight ? HeightLeft + 1 : HeightRight + 1;
}
// 判断是否是 平衡的
bool isBalance(Node* root)
{
if (root == nullptr)
return;
// 记录左右子树的高度
int HeightLeft = Height(root->_left);
int HeightRight = Height(root->_right);
// 判断计算出来的 平衡因子是否和 该结点当中存储的是一样的
if ((HeightLeft - HeightRight) != root->_bf)
{
cout << "平衡因子出错: " << root->_kv.first << "->" << root->_bf << endl;
}
// 递归判断左右子树当中的结点
return abs(HeightLeft - HeightRight) < 2
&& isBalance(root->_left)
&& isBalance(root->_right);
}在外部函数当中调用不了 其中的成员,也就是调用不了 根结点指针,所以我们还是写一个接口:
public:
int Height()
{
return Height(_root);
}
bool isBalance()
{
return isBalance(_root);
}删除结点
AVL树的删除操作比 插入还要困难一些,但是大体上也是三个步骤:
- 按照搜索树的规则查找结点删除
- 更新平衡因子
- 判断平衡因子是否符合规则,不符合就要旋转
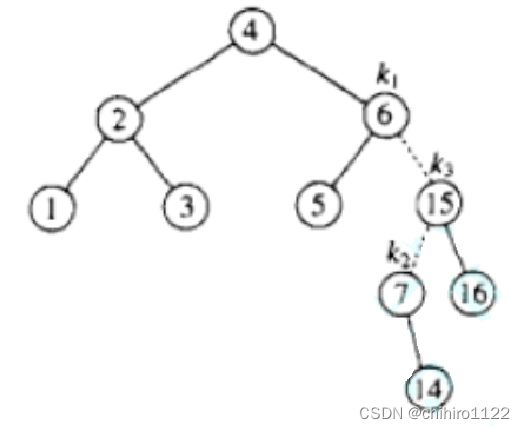
如下述例子:
假设现在要删除结点 3 ,在删除之前 2 的平衡因子是 0 ,3 是 2 的右孩子,当删除3 之后, 2 的平衡因子要 --。2 的平衡因子从 0 减到 -1 ,那么 2 的平衡因子 更新到 -1 ,在插入当中是需要网上更新父亲的平衡因子的,但是在上述例子的删除当中就不需要望山更新,因为 4 的左子树高度 在删除 3 之后,没有变化。
而相反,如果在删除之后,删除结点的父亲的平衡因子 更新到 0 ,在插入当中是不需要网上更新的,但是在插入当中,如果一个结点的平衡因子 更新到0 ,说明该结点的某一个子树肯定发生了高度变化,比如删除上述例子的 14 这个结点,那么 7 结点的平衡因子 就会从 -1 更新到 0。此时就需要往上沿着父亲更新结点。在往上更新过程当中,只要是更新为0 了,都要继续网上更新。
而如果对结点的平衡因子进行更新,和插入当中类似,判断是从 父亲结点左右孩子的那一边更新上来的,从那边上来,就代表有那边的 高度发生了变化,对应的进行修改就好了。
其实上述在查找删除,更新平衡因子都还好,主要是在判断是否需要旋转的条件才是麻烦的。
不能再像 插入当中判断 是否需要旋转一样 ,沿着更新父亲结点的平衡因子路径上,判断更新之后父亲结点的平衡因子是否合法。
因为在删除结点之后,不是在删除路径的一边子树当中去判断旋转,因为此时多出来的高度的子树来,某一个平衡因子不合法的结点的另一边子树当中。找到平衡因子不合法的结点还不够,还需要找到使得这个结点为根结点的子树不平衡的子树。当然,这种情况是双旋的情况,如果是单旋就还好,不过双旋的问题可能是要解决的。
关于删除细节在 《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。这两本书当中就有详细的介绍。
AVL树的性能
AVL树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过1,这
样可以保证查询时高效的时间复杂度,即O(log N)。
但是如果要对AVL树做一些结构修改的操作,非常麻烦,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。
但是,AVL树本来就为了方便我们快速查找数据的,当插入好了之后,AVL树构建好了,我们在查找数据的时候会非诚的方便。
所以,AVL树一般用于静态的存储数据,比如你在一开始就把数据以AVL树的结果构建好,那么之后尽量少更改数据,建议不更改其中的数据,那么AVL树在只是查找数据方便还是非常方便的。
而且,AVL虽然在旋转上看似很复杂,其实性能上没有太大消耗,在旋转当中,没有旋转,只是单纯的修改链接指针和 修改平衡因子,这些都是常数级别的 时间复杂度。
所以,AVL树只是看似复杂,但是实际在使用过程当中的效率还是挺高的,比如下述程序:
void text2()
{
AVLTree AVLT;
vector v;
int N = 10000;
v.reserve(10000);
srand(time(0));
// 开始计时
int start = clock();
for (int i = 0; i < N; i++)
{
v.push_back(rand());
}
for (const auto& e : v)
{
AVLT.insert(make_pair(e, e));
//cout << "insert():" << e << "->" << AVLT.isBalance() << endl;
}
cout << AVLT.isBalance() << endl;
int end = clock();
cout << "用时: " << (double)(end - start)/ CLOCKS_PER_SEC << "s" << endl;
} 如上述程序,使用clock ()函数来计算整个程序的执行时间。
我们随机插入了 10000 个数据,而且还是用了 isBalance()这个效率不太好的递归函数去判断这个 树是不是 AVL树,输出:
1
用时: 0.006s可以看到,耗时 0.006 s。