牛客编程题--必刷101之递归回溯篇

补充知识

该补充知识内容是参考laluladong作者的算法文档

回溯算法

回溯算法实际上是一个类似枚举的搜索尝试过程，主要是在搜索尝试过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。许多复杂的，规模较大的问题都可以使用回溯法，有“通用解题方法”的美称。

解决⼀个回溯问题，实际上就是⼀个决 策树的遍历过程
你只需要思考 3 个问题：
1、路径：也就是已经做出的选择。
2、选择列表：也就是你当前可以做的选择。
3、结束条件：也就是到达决策树底层，⽆法再做选择的条件。

回溯算法的框架：

result = [] 
def backtrack(路径, 选择列表): 
	if 满⾜结束条件: 
		result.add(路径) 
		return 
	for 选择 in 选择列表: 
		做选择 
		backtrack(路径, 选择列表) 
		撤销选择

经典问题之全排列

在⾼中的时候就做过排列组合的数学题，我们也知道 n 个不重复的数，全排列共有 n! 个。
举例说明：⽐⽅说给三个数 [1,2,3] ，你肯定 不会⽆规律地乱穷举，⼀般是这样： 先固定第⼀位为 1，然后第⼆位可以是 2，那么第三位只能是 3；然后可以 把第⼆位变成 3，第三位就只能是 2 了；然后就只能变化第⼀位，变成 2， 然后再穷举后两位

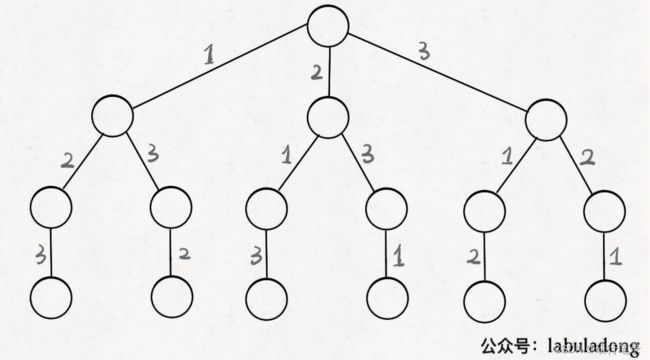
只要从根遍历这棵树，记录路径上的数字，其实就是所有的全排列。我们不妨把这棵树称为回溯算法的【决策树】

为啥说这是决策树呢，因为你在每个节点上其实都在做决策。⽐如说你站在 下图的红⾊节点上：

你现在就在做决策，可以选择 1 那条树枝，也可以选择 3 那条树枝。为啥只 能在 1 和 3 之中选择呢？因为 2 这个树枝在你⾝后，这个选择你之前做过 了，⽽全排列是不允许重复使⽤数字的。
现在可以解答开头的⼏个名词： [2] 就是「路径」，记录你已经做过的选 择； [1,3] 就是「选择列表」，表⽰你当前可以做出的选择；「结束条 件」就是遍历到树的底层，在这⾥就是选择列表为空的时候。

我们定义的 backtrack 函数其实就像⼀个指针，在这棵树上游⾛，同时要正确维护每个节点的属性，每当⾛到树的底层，其「路径」就是⼀个全排列。

List<List<Integer>> res = new LinkedList<>(); 
/* 主函数，输⼊⼀组不重复的数字，返回它们的全排列 */ 
List<List<Integer>> permute(int[] nums) { 
	// 记录「路径」 
	LinkedList<Integer> track = new LinkedList<>(); 
	backtrack(nums, track); 
	return res; 
}

// 路径：记录在 track 中 
// 选择列表：nums 中不存在于 track 的那些元素 
// 结束条件：nums 中的元素全都在 track 中出现 
void backtrack(int[] nums, LinkedList<Integer> track) { 
	// 触发结束条件 	
	if (track.size() == nums.length) { 
		res.add(new LinkedList(track)); 
		return; 
	}
	for (int i = 0; i < nums.length; i++) { 
		// 排除不合法的选择 
		if (track.contains(nums[i])) 
			continue; 
		// 做选择 
		track.add(nums[i]); 
		// 进⼊下⼀层决策树 
		backtrack(nums, track); 
		// 取消选择 
		track.removeLast(); 
	} 
}

N皇后问题

概述：给你⼀个 N×N 的棋盘，让你放置 N 个皇后，使得它们不能互相攻击。
这个问题本质上跟全排列问题差不多，决策树的每⼀层表⽰棋盘上的每⼀行；每个节点可以做出的选择是，在该行的任意⼀列放置⼀个皇后。

vector<vector<string>> res;
/* 输⼊棋盘边⻓ n，返回所有合法的放置 */
vector<vector<string>> solveNQueens(int n) {
	// '.' 表⽰空，'Q' 表⽰皇后，初始化空棋盘。
	vector<string> board(n, string(n, '.'));
	backtrack(board, 0);
	return res;
}
// 路径：board 中⼩于 row 的那些⾏都已经成功放置了皇后
// 选择列表：第 row ⾏的所有列都是放置皇后的选择
// 结束条件：row 超过 board 的最后⼀⾏
void backtrack(vector<string>& board, int row) {
	// 触发结束条件
	if (row == board.size()) {
	res.push_back(board);
	return;
	}
	int n = board[row].size();
	for (int col = 0; col < n; col++) {
		// 排除不合法选择
		if (!isValid(board, row, col))
		continue;
		// 做选择
		board[row][col] = 'Q';
		// 进⼊下⼀⾏决策
		backtrack(board, row + 1);
		// 撤销选择
		board[row][col] = '.';
		}
}

isValid 函数的实现也很简单：

/* 是否可以在 board[row][col] 放置皇后？ */
bool isValid(vector<string>& board, int row, int col) {
	int n = board.size();
	// 检查列是否有皇后互相冲突
	for (int i = 0; i < n; i++) {
		if (board[i][col] == 'Q')
		return false;
	}
	// 检查右上⽅是否有皇后互相冲突
	for (int i = row - 1, j = col + 1;i >= 0 && j < n; i--, j++) {
		if (board[i][j] == 'Q')
		return false;
	}
	// 检查左上⽅是否有皇后互相冲突
	for (int i = row - 1, j = col - 1;i >= 0 && j >= 0; i--, j--) {
		if (board[i][j] == 'Q')
		return false;
	}
	return true;
}

函数 backtrack 依然像个在决策树上游⾛的指针，通过 row 和 col 就可以表⽰函数遍历到的位置，通过 isValid 函数可以将不符合条件的情况剪枝：

当 N = 8 时，就是八皇后问题，数学⼤佬⾼斯穷尽一生都没有数清楚八皇后问题到底有几种可能的放置⽅法，但是我们的算法只需要⼀秒就可以算出来所有可能的结果。

有的时候，我们并不想得到所有合法的答案，只想要⼀个答案，怎么办呢？

// 函数找到⼀个答案后就返回 true
bool backtrack(vector<string>& board, int row) {
	// 触发结束条件
	if (row == board.size()) {
		res.push_back(board);
		return true;
	}
	...
	for (int col = 0; col < n; col++) {
		...
		board[row][col] = 'Q';
		if (backtrack(board, row + 1))
			return true;
		board[row][col] = '.';
	}
	return false;
}

1、没有重复项数字的全排列

题目描述：给出一组数字，返回该组数字的所有排列
例如：
[1,2,3]的所有排列如下
[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2], [3,2,1].
（以数字在数组中的位置靠前为优先级，按字典序排列输出。）

输入：[1,2,3]
返回值：[[1,2,3],[1,3,2],[2,1,3],[2,3,1],[3,1,2],[3,2,1]]

回溯 + 递归

因为牛客上给出的数据类型为ArrayList，因此在进行回溯的方法过程中会有所不同，但是回溯的具体思想还是如此。
//遍历后续的元素

for(int i = index; i < num.size(); i++){ 
    //交换二者
    swap(num, i, index); 
    //继续往后找
    recursion(res, num, index + 1); 
    //回溯
    swap(num, i, index); 

step 1：先将数组排序，获取字典序最小的排列情况。
step 2：递归的时候根据当前下标，遍历后续的元素，交换二者位置后，进入下一层递归。
step 3：处理完一分支的递归后，将交换的情况再换回来进行回溯，进入其他分支。
step 4：当前下标到达数组末尾就是一种排列情况。

import java.util.*;

public class Solution {
    public ArrayList<ArrayList<Integer>> permute(int[] num) {
//         step 1：先将数组排序，获取字典序最小的排列情况。
//         step 2：递归的时候根据当前下标，遍历后续的元素，交换二者位置后，进入下一层递归。
//         step 3：处理完一分支的递归后，将交换的情况再换回来进行回溯，进入其他分支。
//         step 4：当前下标到达数组末尾就是一种排列情况。
        Arrays.sort(num);
        ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
        ArrayList<Integer> nums = new ArrayList<Integer>();
        // 数组转ArrayList
        for(int i =0 ; i< num.length;i++){
            nums.add(num[i]);
        }
        //
        backtrack(res,nums,0);
        return res;
    }
    private void swap(ArrayList<Integer> nums, int i,int j){
        int temp = nums.get(i);
        nums.set(i,nums.get(j));
        nums.set(j,temp);
        
    }
    private void backtrack(ArrayList<ArrayList<Integer>> res, ArrayList<Integer> nums, int index){
        // 结束条件
        if(index == nums.size()-1){
            res.add(nums);
        }
        for(int i = index; i<nums.size();i++){
            // 交换
            swap(nums,i,index);
            backtrack(res,nums,index+1);
            // 回溯
	        swap(nums,i,index);
        }
    }
}

2、有重复项数字的全排列

题目描述：给出一组可能包含重复项的数字，返回该组数字的所有排列。结果以字典序升序排列。

输入：[1,1,2]
返回值：[[1,1,2],[1,2,1],[2,1,1]]

这道题类似没有重复项数字的全排列，但是因为交换位置可能会出现相同数字交换的情况，出现的结果需要去重，因此不便于使用交换位置的方法。

方案：使用临时数组去组装一个排列的情况
每当我们选取一个数组元素以后，就确定了其位置，相当于对数组中剩下的元素进行全排列添加在该元素后面，给剩余部分进行全排列就是一个子问题，因此可以使用递归。
终止条件： 临时数组中选取了n个元素，已经形成了一种排列情况了，可以将其加入输出数组中。
返回值： 每一层给上一层返回的就是本层级在临时数组中添加的元素，递归到末尾的时候就能添加全部元素。
本级任务： 每一级都需要选择一个不重复元素加入到临时数组末尾（遍历数组选择）。

回溯的思想也与没有重复项数字的全排列类似，对于数组[1,2,2,3]，如果事先在临时数组中加入了1，后续子问题只能是[2,2,3]的全排列接在1后面，对于2开头的分支达不到，因此也需要回溯：将临时数组刚刚加入的数字pop掉，同时vis修改为没有加入，这样才能正常进入别的分支。

/标记为使用过
vis[i] =  true;  
//加入数组
temp.add(num[i]); 
recursion(res, num, temp, vis);
//回溯
vis[i] =  false; 
temp.remove(temp.size() - 1);

具体步骤：
step 1：先对数组按照字典序排序，获取第一个排列情况。
step 2：准备一个数组暂存递归过程中组装的排列情况。使用额外的vis数组用于记录哪些位置的数字被加入了。
step 3：每次递归从头遍历数组，获取数字加入：首先根据vis数组，已经加入的元素不能再次加入了；同时，如果当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用，也不需要将其纳入。
step 4：进入下一层递归前将vis数组当前位置标记为使用过。
step 5：回溯的时候需要修改vis数组当前位置标记，同时去掉刚刚加入数组的元素，
step 6：临时数组长度到达原数组长度就是一种排列情况。

import java.util.*;
public class Solution {
    public void recursion(ArrayList<ArrayList<Integer>> res, int[] num, ArrayList<Integer> temp, Boolean[] vis){
        //临时数组满了加入输出 
        if(temp.size() == num.length){
            res.add(new ArrayList<Integer>(temp));
            return;
        }
        //遍历所有元素选取一个加入
        for(int i = 0; i < num.length; i++){
            //如果该元素已经被加入了则不需要再加入了
            if(vis[i])
                continue;
            if(i > 0 && num[i - 1] == num[i] && !vis[i - 1])
                //当前的元素num[i]与同一层的前一个元素num[i-1]相同且num[i-1]已经用过了
                continue;
            //标记为使用过
            vis[i] =  true;
            //加入数组
            temp.add(num[i]);
            recursion(res, num, temp, vis);
            //回溯
            vis[i] =  false;
            temp.remove(temp.size() - 1);
        }
    }
    public ArrayList<ArrayList<Integer>> permuteUnique(int[] num) {
        //先按字典序排序
        Arrays.sort(num);
        Boolean[] vis = new Boolean[num.length];
        Arrays.fill(vis, false);
        ArrayList<ArrayList<Integer> > res = new ArrayList<ArrayList<Integer>>();
        ArrayList<Integer> temp = new ArrayList<Integer>();
        recursion(res, num, temp, vis);
        return res;}
}

3、岛屿数量

题目描述：给一个01矩阵，1代表是陆地，0代表海洋， 如果两个1相邻，那么这两个1属于同一个岛。我们只考虑上下左右为相邻。
岛屿: 相邻陆地可以组成一个岛屿（相邻:上下左右） 判断岛屿个数。

输入
[
[1,1,0,0,0],
[0,1,0,1,1],
[0,0,0,1,1],
[0,0,0,0,0],
[0,0,1,1,1]
]
对应的输出为3
(注：存储的01数据其实是字符’0’,‘1’)

题目分析：深度优先遍历(DFS)
深度优先搜索一般用于树或者图的遍历，其他有分支的（如二维矩阵）也适用。它的原理是从初始点开始，一直沿着同一个分支遍历，直到该分支结束，然后回溯到上一级继续沿着一个分支走到底，如此往复，直到所有的节点都有被访问到。

矩阵中多处聚集着1，要想统计1聚集的堆数而不重复统计，那我们可以考虑每次找到一堆相邻的1，就将其全部改成0，而将所有相邻的1改成0的步骤又可以使用深度优先搜索（dfs）：当我们遇到矩阵的某个元素为1时，首先将其置为了0，然后查看与它相邻的上下左右四个方向，如果这四个方向任意相邻元素为1，则进入该元素，进入该元素之后我们发现又回到了刚刚的子问题，又是把这一片相邻区域的1全部置为0，因此可以用递归实现。

//后续四个方向遍历
if(i - 1 >= 0 && grid[i - 1][j] == '1') 
    dfs(grid, i - 1, j);
if(i + 1 < n && grid[i + 1][j] == '1') 
    dfs(grid, i + 1,j);
if(j - 1 >= 0 && grid[i][j - 1] == '1') 
    dfs(grid, i, j - 1);
if(j + 1 < m && grid[i][j + 1] == '1') 
    dfs(grid, i, j + 1);

终止条件： 进入某个元素修改其值为0后，遍历四个方向发现周围都没有1，那就不用继续递归，返回即可，或者递归到矩阵边界也同样可以结束。
返回值： 每一级的子问题就是把修改后的矩阵返回，因为其是函数引用，也不用管。
本级任务： 对于每一级任务就是将该位置的元素置为0，然后查询与之相邻的四个方向，看看能不能进入子问题。

具体步骤：
step 1：优先判断空矩阵等情况。
step 2：从上到下从左到右遍历矩阵每一个位置的元素，如果该元素值为1，统计岛屿数量。
step 3：接着将该位置的1改为0，然后使用dfs判断四个方向是否为1，分别进入4个分支继续修改。

import java.util.*;


public class Solution {
    /**
     * 判断岛屿数量
     * @param grid char字符型二维数组 
     * @return int整型
     */
    
    private void dfs(char[][] grid, int i, int j){
        int n = grid.length;
        int m = grid[0].length;
        // 首先将grid[i][j]置0
        grid[i][j] ='0';
        // 开始遍历其他方向
        if(i-1 >=0 && grid[i-1][j]=='1')
            dfs(grid,i-1,j);
        if( i+1 < n && grid[i+1][j] == '1')
            dfs(grid,i+1,j);
        if( j-1 >=0&& grid[i][j-1]== '1')
            dfs(grid, i,j-1);
        if( j+1 < m && grid[i][j+1]== '1')
            dfs(grid,i,j+1);
    }
    
    public int solve (char[][] grid) {
        // 代表二维数组的长度
        int n = grid.length;
        if(n == 0)
            return 0;
        int m = grid[0].length;
        // 记录岛屿数
        int count = 0;
        // 遍历二维数组
        for(int i =0; i< n; i++){
            for(int j=0; j<m; j++){
                // 判断1的情况
                if(grid[i][j]== '1'){
                    // 开始计数
                    count ++;
                    // 通过dfs来判断相邻是否是同一岛屿
                    dfs(grid,i,j);
                }
            }
        }
        return count;
        
    }
}

4、字符串的排列

题目描述：输入一个长度为 n 字符串，打印出该字符串中字符的所有排列，你可以以任意顺序返回这个字符串数组。
例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。

输入：“ab”
返回值：[“ab”,“ba”]
说明：返回[“ba”,“ab”]也是正确的

思路：都是求元素的全排列，字符串与数组没有区别，一个是数字全排列，一个是字符全排列，因此大致思路与有重复项数字的全排列类似，只是这道题输出顺序没有要求。但是为了便于去掉重复情况，我们还是应该参照数组全排列，优先按照字典序排序，因为排序后重复的字符就会相邻，后续递归找起来也很方便。

跟有重复项数字的全排列的题目解题方案类似
终止条件： 临时字符串中选取了n个元素，已经形成了一种排列情况了，可以将其加入输出数组中。
返回值： 每一层给上一层返回的就是本层级在临时字符串中添加的元素，递归到末尾的时候就能添加全部元素。
本级任务： 每一级都需要选择一个元素加入到临时字符串末尾（遍历原字符串选择）。

具体步骤：
step 1：先对字符串按照字典序排序，获取第一个排列情况。
step 2：准备一个空串暂存递归过程中组装的排列情况。使用额外的vis数组用于记录哪些位置的字符被加入了。
step 3：每次递归从头遍历字符串，获取字符加入：首先根据vis数组，已经加入的元素不能再次加入了；同时，如果当前的元素str[i]与同一层的前一个元素str[i-1]相同且str[i-1]已经用，也不需要将其纳入。
step 4：进入下一层递归前将vis数组当前位置标记为使用过。
step 5：回溯的时候需要修改vis数组当前位置标记，同时去掉刚刚加入字符串的元素，
step 6：临时字符串长度到达原串长度就是一种排列情况。

import java.util.*;
public class Solution {
    
    public void recursion(ArrayList<String> res, char[] str, StringBuffer temp, boolean[] vis){
        //临时字符串满了加入输出 fast-template
        if(temp.length() == str.length){
            res.add(new String(temp));
            return;
        }
        //遍历所有元素选取一个加入
        for(int i = 0; i < str.length; i++){
            //如果该元素已经被加入了则不需要再加入了
            if(vis[i])
                continue;
            if(i > 0 && str[i - 1] == str[i] && !vis[i - 1])
                //当前的元素str[i]与同一层的前一个元素str[i-1]相同且str[i-1]已经用过了
                continue;
            //标记为使用过
            vis[i] = true;
            //加入临时字符串
            temp.append(str[i]);
            recursion(res, str, temp, vis);
            //回溯
            vis[i] = false;
            temp.deleteCharAt(temp.length() - 1);
        }
    }
    
    
    public ArrayList<String> Permutation(String str) {
        ArrayList<String> res = new ArrayList<String>();
        if(str ==null || str.length() ==0)
            return res;
        // 转成数组
        char[] charstr = str.toCharArray();
        Arrays.sort(charstr);
        boolean [] vis = new boolean[str.length()];
        Arrays.fill(vis, false);
        StringBuffer temp = new StringBuffer();
        //递归获取
        recursion(res,charstr,temp,vis);
        return res;
        
        
    }
}

4、N皇后问题

题目描述：N 皇后问题是指在 n * n 的棋盘上要摆 n 个皇后，
要求：任何两个皇后不同行，不同列也不在同一条斜线上，求给一个整数 n ，返回 n 皇后的摆法数。

例如当输入4时，对应的返回值为2，对应的两种四皇后摆位如下图所示：

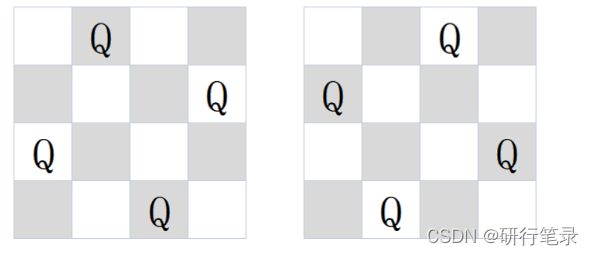
解题思路：递归
n个皇后，不同行不同列，那么肯定棋盘每行都会有一个皇后，每列都会有一个皇后。如果我们确定了第一个皇后的行号与列号，则相当于接下来在n−1行中查找n−1个皇后，这就是一个子问题，因此使用递归：
终止条件： 当最后一行都被选择了位置，说明n个皇后位置齐了，增加一种方案数返回。
返回值： 每一级要将选中的位置及方案数返回。
本级任务： 每一级其实就是在该行选择一列作为该行皇后的位置，遍历所有的列选择一个符合条件的位置加入数组，然后进入下一级。

具体步骤：
step 1：对于第一行，皇后可能出现在该行的任意一列，我们用一个数组pos记录皇后出现的位置，下标为行号，元素值为列号。
step 2：如果皇后出现在第一列，那么第一行的皇后位置就确定了，接下来递归地在剩余的n−1行中找n−1个皇后的位置。
step 3：每个子问题检查是否符合条件，我们可以对比所有已经记录的行，对其记录的列号查看与当前行列号的关系：即是否同行、同列或是同一对角线。

import java.util.*;

public class Solution {
    /**
     * 
     * @param n int整型 the n
     * @return int整型
     */
    private int res;
    // 判断皇后是否符合条件
    public boolean isValid(int[] pos, int row,int col){
        for(int i=0; i< row;i++){
            // 不能同行同列同一斜线
            if(row == i || col == pos[i] || Math.abs(row - i) == Math.abs(col - pos[i]))
                return false;
        }
        return  true;
    }
    
    // 递归查找皇后种类
    public void recursion(int n, int row, int[] pos){
        // 完成全部行选择位置
        if(n == row){
            res++;
            return;
        }
        // 遍历所有列
        for(int i = 0; i < n; i++){
            //检查位置是否符合条件
            if(isValid(pos, row,i)){
                pos[row] = i;
                // 递归继续查找
                recursion(n,row + 1, pos);
            }
         }
    }
    
    public int Nqueen (int n) {
        res = 0;
        int[] pos = new int[n];
        Arrays.fill(pos, 0);
        // 递归
        recursion(n, 0, pos);
        return res;
    }
}

5、括号生成

题目描述：给出n对括号，请编写一个函数来生成所有的由n对括号组成的合法组合。
例如，给出n=3，解集为：
“((()))”, “(()())”, “(())()”, “()()()”, “()(())”

输入：1
返回值：[“()”]
输入：2
返回值：[“(())”,“()()”]

解题思路：递归
相当于一共n个左括号和n个右括号，可以给我们使用，我们需要依次组装这些括号。每当我们使用一个左括号之后，就剩下n−1个左括号和n个右括号给我们使用，结果拼在使用的左括号之后就行了，因此后者就是一个子问题，可以使用递归：
终止条件： 左右括号都使用了n个，将结果加入数组。
返回值： 每一级向上一级返回后续组装后的字符串，即子问题中搭配出来的括号序列。
本级任务： 每一级就是保证左括号还有剩余的情况下，使用一次左括号进入子问题，或者右括号还有剩余且右括号使用次数少于左括号的情况下使用一次右括号进入子问题。

具体步骤：
step 1：将空串与左右括号各自使用了0个送入递归。
step 2：若是左右括号都使用了n个，此时就是一种结果。
step 3：若是左括号数没有到达n个，可以考虑增加左括号，或者右括号数没有到达n个且左括号的使用次数多于右括号就可以增加右括号。

import java.util.*;


public class Solution {
    /**
     * 
     * @param n int整型 
     * @return string字符串ArrayList
     */
    public void recursion(int left, int right, String temp, ArrayList<String> res, int n){
        // 左右括号都用完了，直接把结果加入
        if(left == n && right == n){
            res.add(temp);
            return;
        }
        //  使用一次左括号
        if(left < n){
            recursion(left+1,right, temp + "(", res, n);
        }
        // 使用右括号个数必须少于左
        if(right < n && left > right)
            recursion(left , right +1 ,temp + ")", res , n);
    }
    
    public ArrayList<String> generateParenthesis (int n) {
        // 记录结果
        ArrayList<String> res = new ArrayList<String>();
        // 递归
        recursion(0, 0, "",res, n);
        return res;
    }
}

6、矩阵最长递增路径

题目描述：给定一个 n 行 m 列矩阵 matrix ，矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径，使这条路径上的元素是递增的。并输出这条最长路径的长度。
这个路径必须满足以下条件：

1. 对于每个单元格，你可以往上，下，左，右四个方向移动。 你不能在对角线方向上移动或移动到边界外。
2. 你不能走重复的单元格。即每个格子最多只能走一次。

例如：当输入为[[1,2,3],[4,5,6],[7,8,9]]时，对应的输出为5，
其中的一条最长递增路径如下图所示：

输入：[[1,2,3],[4,5,6],[7,8,9]]
返回值：5
说明：1->2->3->6->9即可。当然这种递增路径不是唯一的。

输入：[[1,2],[4,3]]
返回值：4
说明： 1->2->3->4

解题思路：递归

深度优先搜索（dfs）

补充知识
深度优先搜索：一般用于树或者图的遍历，其他有分支的（如二维矩阵）也适用。它的原理是从初始点开始，一直沿着同一个分支遍历，直到该分支结束，然后回溯到上一级继续沿着一个分支走到底，如此往复，直到所有的节点都有被访问到。

思路：既然是查找最长的递增路径长度，那我们首先要找到这个路径的起点，起点不好直接找到，就从上到下从左到右遍历矩阵的每个元素。然后以每个元素都可以作为起点查找它能到达的最长递增路径。

如何查找以某个点为起点的最长递增路径呢？我们可以考虑深度优先搜索，因为我们查找递增路径的时候，每次选中路径一个点，然后找到与该点相邻的递增位置，相当于进入这个相邻的点，继续查找递增路径，这就是递归的子问题。因此递归过程如下：

终止条件： 进入路径最后一个点后，四个方向要么是矩阵边界，要么没有递增的位置，路径不能再增长，返回上一级。
返回值： 每次返回的就是本级之后的子问题中查找到的路径长度加上本级的长度。
本级任务： 每次进入一级子问题，先初始化后续路径长度为0，然后遍历四个方向（可以用数组表示，下标对数组元素的加减表示去往四个方向），进入符合不是边界且在递增的邻近位置作为子问题，查找子问题中的递增路径长度。因为有四个方向，所以最多有四种递增路径情况，因此要维护当级子问题的最大值。

具体步骤：
step 1：使用一个dp数组记录i，j处的单元格拥有的最长递增路径，这样在递归过程中如果访问到就不需要重复访问。
step 2：遍历矩阵每个位置，都可以作为起点，并维护一个最大的路径长度的值。
step 3：对于每个起点，使用dfs查找最长的递增路径：只要下一个位置比当前的位置数字大，就可以深入，同时累加路径长度。

import java.util.*;


public class Solution {
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 递增路径的最大长度
     * @param matrix int整型二维数组 描述矩阵的每个数
     * @return int整型
     */
    // 记录四个方向
    private int[][] dirs = new int[][]{{-1,0},{1,0},{0,-1},{0,1}};
    private int n,m;
    
    public int dfs(int[][] matrix, int [][] dp,int i, int j){
        if(dp[i][j] != 0)
            return dp[i][j];
        dp[i][j]++;
        for(int k = 0;k< 4;k++){
            int nexti = i + dirs[k][0];
            int nextj = j + dirs[k][1];
            if(nexti >=0 && nexti< n && nextj >=0 && nextj < m && matrix[nexti][nextj] > matrix[i][j]){
                dp[i][j] = Math.max(dp[i][j],dfs(matrix,dp,nexti,nextj)+1);
            }
        }
        return dp[i][j];
    }
    
    
    public int solve (int[][] matrix) {
        // 判断矩阵是否为空
        if(matrix.length == 0 || matrix[0].length ==0)
            return 0;
        int res = 0;
        n = matrix.length;
        m = matrix[0].length;
        
        int [][] dp = new int[n+1][m+1];
        for(int i = 0; i< n ;i++){
            for(int j = 0; j< m;j++){
                res = Math.max(res,dfs(matrix,dp,i,j));
            }
        }
        return res;
        
        
    }
}