岛屿数量------DFS&BFS
岛屿数量------DFS&BFS
1 问题简介
LeetCode-200
给你一个由 ‘1’(陆地)和 ‘0’(水)组成的的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1输入:grid = [
[“1”,“1”,“0”,“0”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“1”,“0”,“0”],
[“0”,“0”,“0”,“1”,“1”]
]
输出:3
2 思路
首先在看到这样充满0,1的数组,我会想到无向图的一种表现形式。‘1’表示结点,‘0’表示结点与结点不连通。若将这样的输入数组看作图,我们很容易想到图的遍历。通过遍历获取图中所有连接在一起的 ‘1’,有多少块这样连接起来的 ‘1’,就有多少块岛屿。
例如输入样例1中,所有连同的 ‘1’只组成了一块岛屿。
了解清楚我们需要获取的信息,我们就可以开始想怎么获取这样的信息。
遍历图,我们首先想到的就是深度优先搜索(dfs)以及宽度优先搜索(bfs)。
2.1 深度优先搜索(dfs)
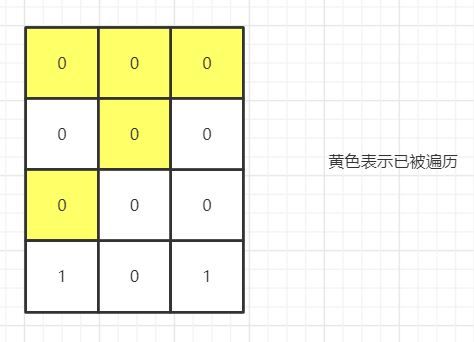
从第一个 ‘1’ 开始,不断遍历向深度更大的 ’1‘,表现在数组的形式上就是,向 ’1‘的四个方向–上下左右,不断往深度遍历。遍历完 ’1‘的上方,遍历下方,接着遍历左方,最后遍历右方。遍历过的位置将其置 ’0‘ 防止重复遍历。通过递归可以很容易实现这个过程。
下面是遍历图解:
1、初始数组
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-6653yQpx-1618065537384)(http://cdn.zengzhizhao.com/岛屿数量1.JPG)]
2、从第一个元素开始遍历,’1‘遍历过后被置 ’0‘。
3、向更深处遍历
4、继续深度遍历,到达最深处
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-wtZKArNd-1618065537390)(http://cdn.zengzhizhao.com/岛屿数量4.JPG)]
5、开始回溯
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-HUKKtkfC-1618065537392)(http://cdn.zengzhizhao.com/岛屿数量5.JPG)]
6、一个岛屿遍历完毕,开始遍历下一个岛屿。
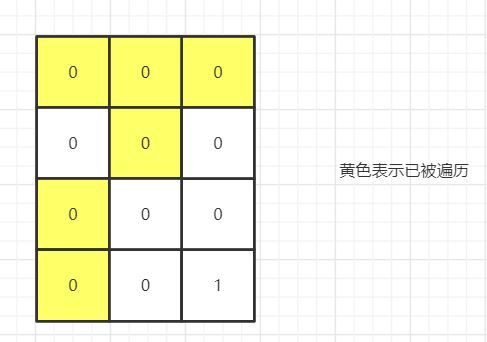
7、又遍历完一共岛屿,现岛屿数为2
8、最后一个元素上下左右方向都没有 ’1‘,最终岛屿数为3
代码实现:
class Solution {
int row;
int col;
public int numIslands(char[][] grid) {
int ans = 0;
row = grid.length; //数组大小
col = grid[0].length;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid[i][j] == '1'){
ans++;
dfs(grid, i, j);
}
}
}
return ans;
}
public void dfs(char[][] grid, int r, int c){
//数组越界以及当前元素为’0‘直接返回
if(r<0 || c<0 || c>=col || r>=row || grid[r][c] == '0') return;
//将遍历过的位置 置’0‘
grid[r][c] = '0';
//向四个方向深度遍历
dfs(grid, r+1, c);
dfs(grid, r-1, c);
dfs(grid, r, c-1);
dfs(grid, r, c+1);
}
}
2.2 广度优先搜索(bfs)
广度优先遍历的大致思路与深度优先遍历类似,都是找到相互连通的 ’1‘。只是遍历方式由不断向深度探索,变成了不断向广度探索。
针对每个 ’1‘ 都探索四个方向,即与其相邻的 ’1‘ .而深度优先遍历是向一个方向一直探索直到遇到边界或者遇到 ’0‘,才转换方向。
在这个过程我们需要使用到一个队列来帮助我们存储每个 ’1‘ 的相邻结点。每次都取出队头元素,探索其相邻结点,直到队列为空。
代码实现:
class Solution {
int row;
int col;
public int numIslands(char[][] grid) {
int ans = 0;
row = grid.length;
col = grid[0].length;
for(int i = 0; i < row; i++){
for(int j = 0; j < col; j++){
if(grid[i][j] == '1'){
ans++;
bfs(grid, i, j);
}
}
}
return ans;
}
public void bfs(char[][] grid, int r, int c){
Queue<int[]> queue = new LinkedList<>();
queue.add(new int[]{r, c});
while(!queue.isEmpty()){
int[] temp = queue.poll();
int i = temp[0];
int j = temp[1];
if(i >= 0 && i < row && j >= 0 && j < col && grid[i][j] == '1'){
grid[i][j] = '0';
queue.offer(new int[]{i+1, j});
queue.offer(new int[]{i-1, j});
queue.offer(new int[]{i, j-1});
queue.offer(new int[]{i, j+1});
}
}
}
}
3 总结
观察到所有连通的 ’1‘可以组成一个岛屿,我们就可以考虑遍历所有连通的1.其实还有一种可考虑的方法,那就是把所有连通的 ’1‘看作是一共集合。有多少个集合就有多少个岛屿。通过并查集可以实现将连通的 ’1‘放到一共集合中。但是在这里使用并查集的效率并不比图搜索算法高,所有放到并查集的文章中再讨论吧。