【LeetCode刷题】数组中的第K个最大元素
数组中的第K个最大元素
题目描述:
给定整数数组 nums 和整数 k,请返回数组中第 k 个最大的元素。
请注意,你需要找的是数组排序后的第 k 个最大的元素,而不是第 k 个不同的元素。
你必须设计并实现时间复杂度为 O(n) 的算法解决此问题。
示例 1:
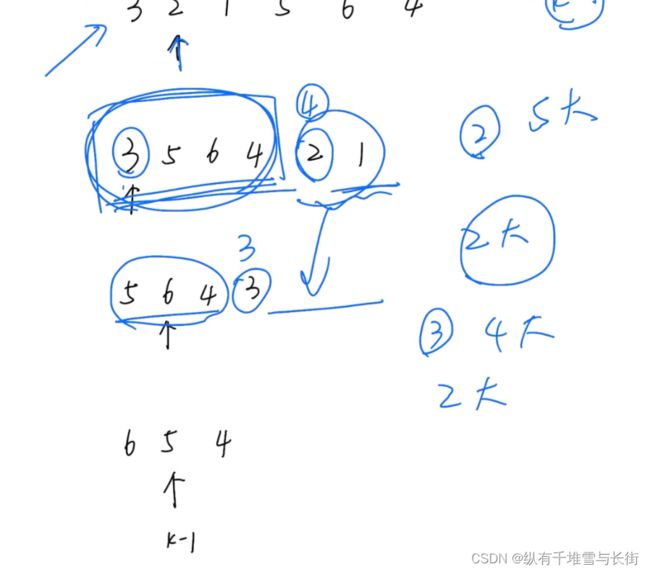
输入: [3,2,1,5,6,4], k = 2
输出: 5
示例 2:
输入: [3,2,3,1,2,4,5,5,6], k = 4
输出: 4
思路:
class Solution {
// Leetcode 215. Kth Largest Element in an Array
// Sort
// N is the size of nums
// Time Complexity: O(NlogN)
// Space Complexity: O(1)
public int findKthLargest(int[] nums, int k) {
Arrays.sort(nums);
return nums[nums.length - k];
}
}
js算法
let findKthLargest = function(nums, k) {
nums.sort((a, b) => b - a).slice(0, k);
return nums[k-1]
};
class Solution {
// Leetcode 215. Kth Largest Element in an Array
// Heap
// N is the size of nums
// Time Complexity: O(NlogK)
// Space Complexity: O(1)
public int findKthLargest(int[] nums, int k) {
// Min heap
PriorityQueue<Integer> pq = new PriorityQueue<>();
for (int num: nums) {
pq.add(num);
if (pq.size() > k) {
pq.poll();
}
}
return pq.peek();
}
}
js代码:构造前 k 个最大元素小顶堆,取堆顶
let findKthLargest = function(nums, k) {
// 从 nums 中取出前 k 个数,构建一个小顶堆
let heap = [,], i = 0
while(i < k) {
heap.push(nums[i++])
}
buildHeap(heap, k)
// 从 k 位开始遍历数组
for(let i = k; i < nums.length; i++) {
if(heap[1] < nums[i]) {
// 替换并堆化
heap[1] = nums[i]
heapify(heap, k, 1)
}
}
// 返回堆顶元素
return heap[1]
};
// 原地建堆,从后往前,自上而下式建小顶堆
let buildHeap = (arr, k) => {
if(k === 1) return
// 从最后一个非叶子节点开始,自上而下式堆化
for(let i = Math.floor(k/2); i>=1 ; i--) {
heapify(arr, k, i)
}
}
// 堆化
let heapify = (arr, k, i) => {
// 自上而下式堆化
while(true) {
let minIndex = i
if(2*i <= k && arr[2*i] < arr[i]) {
minIndex = 2*i
}
if(2*i+1 <= k && arr[2*i+1] < arr[minIndex]) {
minIndex = 2*i+1
}
if(minIndex !== i) {
swap(arr, i, minIndex)
i = minIndex
} else {
break
}
}
}
// 交换
let swap = (arr, i , j) => {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
class Solution {
// Leetcode 215. Kth Largest Element in an Array
// Quick Sort
// N is the size of nums
// Time Complexity: O(N)
// Space Complexity: O(logN)
public int findKthLargest(int[] nums, int k) {
return quickSort(nums, 0, nums.length-1, k);
}
public int quickSort(int[] nums, int l, int r, int k) {
int index = randomParition(nums, l, r);
if (index == k-1) {
return nums[index];
} else {
return index > k-1? quickSort(nums, l, index-1, k) : quickSort(nums, index+1, r, k);
}
}
public int randomParition(int[] nums, int l, int r) {
int i = (int) (Math.random()*(r - l))+l;
swap(nums, i, r);
return partition(nums, l, r);
}
public void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
public int partition(int[] nums, int l, int r) {
int pivot = nums[r];
int rightmost = r;
while(l <= r) {
while( l <= r && nums[l] > pivot ) {
l++;
}
while( l <= r && nums[r] <= pivot ) {
r--;
}
if (l <= r) {
swap(nums, l, r);
}
}
swap(nums, l, rightmost);
return l;
}
}
js代码:
let quickSort = (arr) => {
quick(arr, 0 , arr.length - 1)
}
let quick = (arr, left, right) => {
let index
if(left < right) {
// 划分数组
index = partition(arr, left, right)
if(left < index - 1) {
quick(arr, left, index - 1)
}
if(index < right) {
quick(arr, index, right)
}
}
}
// 一次***
let partition = (arr, left, right) => {
// 取中间项为基准
var datum = arr[Math.floor(Math.random() * (right - left + 1)) + left],
i = left,
j = right
// 开始调整
while(i <= j) {
// 左指针右移
while(arr[i] < datum) {
i++
}
// 右指针左移
while(arr[j] > datum) {
j--
}
// 交换
if(i <= j) {
swap(arr, i, j)
i += 1
j -= 1
}
}
return i
}
// 交换
let swap = (arr, i , j) => {
let temp = arr[i]
arr[i] = arr[j]
arr[j] = temp
}
// 测试
let arr = [1, 3, 2, 5, 4]
quickSort(arr)
console.log(arr) // [1, 2, 3, 4, 5]
// 第 2 个最大值
console.log(arr[arr.length - 2]) // 4