Leetcode算法刷题大全
文章目录
-
- 跟着LABLADONG刷题
-
- 100题二叉树
-
- 二叉树、链表、数组的遍历
- 基础知识
-
- 队列、双端队列、栈
- HashMap
- JAVA逻辑运算符
- List
-
- 一维数组
- List
算法题参考链接:
https://github.com/afatcoder/LeetcodeTop 【根据不同公司】
https://programmercarl.com/ 【整体知识点】
这里使用JAVA语言实现。
跟着LABLADONG刷题
100题二叉树
二叉树、链表、数组的遍历
void traverse(TreeNode root) {
if (root == null) {
return;
}
// 前序位置
traverse(root.left);
// 中序位置
traverse(root.right);
// 后序位置
}
/* 迭代遍历数组 */
void traverse(int[] arr) {
for (int i = 0; i < arr.length; i++) {
}
}
/* 递归遍历数组 */
void traverse(int[] arr, int i) {
if (i == arr.length) {
return;
}
// 前序位置
traverse(arr, i + 1);
// 后序位置
}
/* 迭代遍历单链表 */
void traverse(ListNode head) {
for (ListNode p = head; p != null; p = p.next) {
}
}
/* 递归遍历单链表 */
void traverse(ListNode head) {
if (head == null) {
return;
}
// 前序位置
traverse(head.next);
// 后序位置
}
只要是递归形式的遍历,都会有一个前序和后序位置,分别在递归之前和之后。
所谓前序位置,就是刚进入一个节点(元素)的时候,后序位置就是即将离开一个节点(元素)的时候。
你把代码写在不同位置,代码执行的时机也不同:
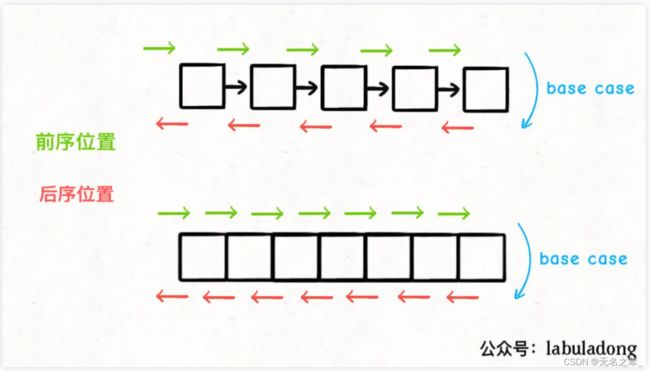
比如说,如果让你倒序打印一条单链表上所有节点的值,你怎么搞?
实现方式当然有很多,但如果你对递归的理解足够透彻,可以利用后序位置:
/* 递归遍历单链表,倒序打印链表元素 */
void traverse(ListNode head) {
if (head == null) {
return;
}
traverse(head.next);
// 后序位置
print(head.val);
}
前中后序是遍历二叉树过程中处理每一个节点的三个特殊时间点,绝不仅仅是三个顺序不同的 List:
前序位置的代码在刚刚进入一个二叉树节点的时候执行;
后序位置的代码在将要离开一个二叉树节点的时候执行;
中序位置的代码在一个二叉树节点左子树都遍历完,即将开始遍历右子树的时候执行。
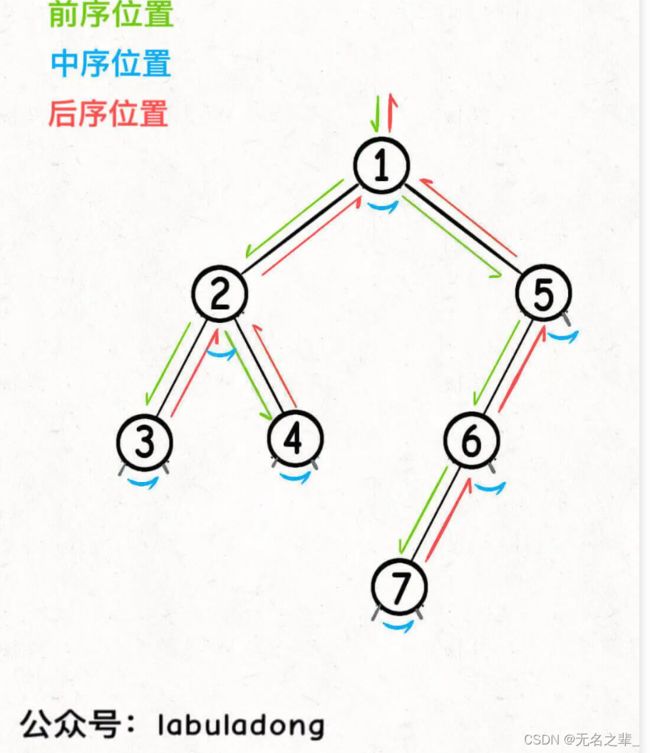
每个节点都有「唯一」属于自己的前中后序位置,所以我说前中后序遍历是遍历二叉树过程中处理每一个节点的三个特殊时间点。
同时多叉树没有唯一的中序位置
二叉树的所有问题,就是让你在前中后序位置注入巧妙的代码逻辑,去达到自己的目的
二叉树题目的递归解法可以分两类思路:
1、遍历一遍二叉树得出答案,
2、通过分解问题计算出答案
这两类思路分别对应着 回溯算法核心框架 和 动态规划核心框架。
基础知识
队列、双端队列、栈
普通队列(一端进另一端出):
Queue queue = new LinkedList()或Deque deque = new LinkedList()
双端队列(两端都可进出)
Deque deque = new LinkedList()
堆栈
Deque deque = new LinkedList()
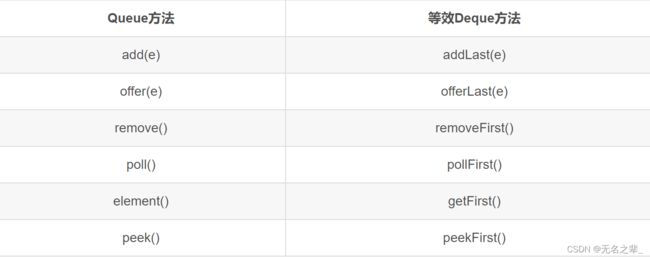
特别的是Duque可以作为栈使用,【亲测,可以使用pop(),push()】

HashMap
// 这里假设map_a存放每个相亲嘉宾序号和年龄的关系
Map<Integer, Integer> map_a = new HashMap<Integer, Integer>();
map_a.containsKey(1);
map_a.put(1,19);
map_a.get(1);//返回19
Java的HashMap中key是不可以重复的,如果重复添加的话,HashMap会自动覆盖key一样的数据,保证一个key对应一个value,使用时只要把一个HashMap里的数据按照key依次加到另一个HashMap里即可。
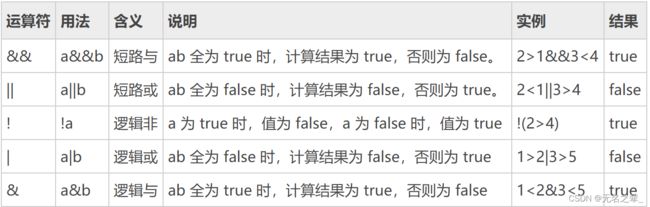
JAVA逻辑运算符
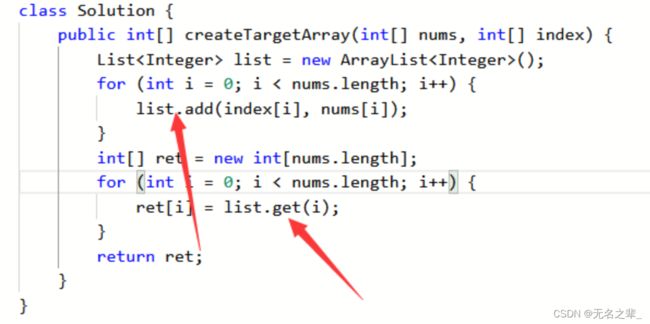
List
一维数组
List
首先List指的是存int类型数据的列表,List指的是存【int类型数据的列表】类型数据的列表------有点“套娃”,大概意思就是这个母列表存子列表,其子列表存int类型的数据。
一、初始化
List res = new ArrayList<>();
或者
Listlist =new ArrayList
();
二、用法
package apackage;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.LinkedList;
class Solution {
public static void main(String[] args) throws ClassNotFoundException {
/* 初始化 */
List<List<Integer>> list = new ArrayList<>();
/* 添加list的层和值 */
/* 方法一 */
list.add(new LinkedList<>()); //先添加层数
list.get(0).add(1); //后在指定层数进行添值:list.get(layers).add(value);
list.add(new LinkedList<>());
list.get(1).add(11);
list.get(1).add(12); //插入第layers+1层的结尾
list.get(1).add(0,13);//插入第layers+1层的开头
/* 方法二 */
list.add(new LinkedList<>(Arrays.asList(1, 2, 3, 6)));
// list.get(2).add(31);//注明:这种表达是错误的,第三层已经由Arrays.asList赋值,无法使用list.get(2).add(31)这个语句
/* 输出list的层数 */
System.out.println("list的层数为: " + list.size());
/*list元素输出*/
System.out.println("方法一:输出list元素");
for (int i = 0; i < list.size(); i++) {
System.out.println(Arrays.toString(list.get(i).toArray()));
}
System.out.println("方法二:输出list元素");
for (int i = 0; i < list.size(); i++) {
List<Integer> item = list.get(i); //item存第i+1层的所有元素
for (int j = 0; j < item.size(); j++) {
System.out.print(item.get(j)+",");
}
System.out.println();
}
/* list元素的删除 */
list.remove(1);//list.remove(i)删除第i+1层所有元素
list.get(1).remove(0); //list.get(i).remove(j)删除第i+1层的第j+1个元素
System.out.println("输出删除后的结果");
for (int i = 0; i < list.size(); i++) {
System.out.println(Arrays.toString(list.get(i).toArray()));
}
}
}
Arrays相关操作
import java.util.Arrays;
fill填充数组
Arrays.fill(a,-1)
数组排序
Arrays.sort(a); // 升序排序,降序比较难
普通数组
int[] piles = new int[4]; // 一旦数组完成初始化,数组在内存中所占的空间将被固定下来,所以数组的长度将不可改变。【这里如果初始化就一定要指定长度】
![]()
初始化默认填充全0
普通数组填充:
for(int i=0; i<amount+1;i++)
dp[i] = Integer.MAX_VALUE;
无穷大
Integer myInf = Integer.MAX_VALUE;
递归操作注意检查
一定要注意边界条件,明确递归函数返回值的意义
动态规划
一定要保证公式是对的,一个等于号都要反复斟酌
如零钱问题,明确dp[i]的含义,明确i的状态变化
0-1
0-1背包问题的公式
二叉树
核心框架
public int traverse(TreeNode root){
if(null) //
// 前序遍历
traverse(root.left);
// 中序遍历
traverse(root.left);
// 后序遍历
}
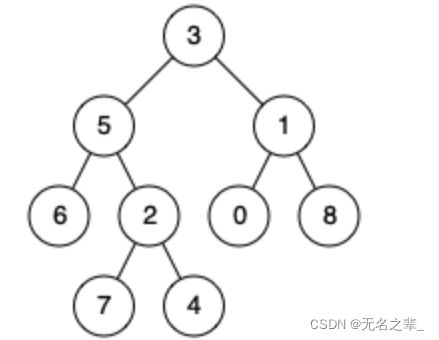
L199. 二叉树的右视图
深度优先算法【用栈】
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
// 深度优先搜索
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> ans = new ArrayList<Integer>();
if(root==null){
return ans;
}
Deque<TreeNode> stack_node = new ArrayDeque<TreeNode>();
Deque<Integer> stack_deep = new ArrayDeque<Integer>();
Map<Integer,TreeNode> map = new HashMap<Integer,TreeNode>();
stack_node.push(root);
stack_deep.push(0);
TreeNode node = root;
int deep;
int max_deep = 0;
while(stack_node.size()!=0){
node = stack_node.pop();
deep = stack_deep.pop();
if(node.left!=null){
stack_node.push(node.left);
stack_deep.push(deep + 1);
}
if(node.right!=null){
stack_node.push(node.right);
stack_deep.push(deep + 1);
}
if(!map.containsKey(deep)){
map.put(deep,node);
max_deep++;
}
}
for(int i=0;i<max_deep;i++){
if(!map.containsKey(i)) break;
ans.add(map.get(i).val);
}
return ans;
}
}
广度优先算法【用队列】
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
// 广度优先搜索
class Solution {
public List<Integer> rightSideView(TreeNode root) {
List<Integer> ans = new ArrayList<Integer>();
if(root==null){
return ans;
}
Queue<TreeNode> stack_node = new ArrayDeque<TreeNode>();
Queue<Integer> stack_deep = new ArrayDeque<Integer>();
Map<Integer,TreeNode> map = new HashMap<Integer,TreeNode>();
stack_node.add(root);
stack_deep.add(0);
TreeNode node = root;
int deep;
int max_deep = 0;
while(stack_node.size()!=0){
node = stack_node.remove();
deep = stack_deep.remove();
if(node.left!=null){
stack_node.add(node.left);
stack_deep.add(deep + 1);
}
if(node.right!=null){
stack_node.add(node.right);
stack_deep.add(deep + 1);
}
// if(!map.containsKey(deep)){
map.put(deep,node);
max_deep++;
// }
}
for(int i=0;i<max_deep;i++){
if(!map.containsKey(i)) break;
ans.add(map.get(i).val);
}
return ans;
}
}
L236. 二叉树的最近公共祖先
做二叉树题目的时候 / 用到递归的时候,先去考虑边界条件。
二叉树某一节点到root的路径是唯一的!!
一定要注意一棵树节点的值是否是唯一的
if(left==null)
return right;
if(right==null)
return left;
return root;
【方法一】笨方法,寻找路径 不知道咋实现
需要遍历2次
在这里插入代码片
【方法二】递归
辅助函数: _findPorQ(root, p, q)
注意辅助函数的定义:以root为根的树,是否能找到P or Q
对于树上任意一个node,分为以下几种情况:
1、如果node.leftnull,就说明接下来要在node.right上找(node.rightnull同理)
2、如果node.right != null 且 node.left != null,就说明当前node就是他们的最近公共祖先。你细品

【你需要考虑:1、边界条件;2、路径上一个节点的递归逻辑】
class Solution {
//
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root==null) return null;
if(root==p) return p;
if(root==q) return q;
TreeNode left = lowestCommonAncestor(root.left, p, q);
TreeNode right = lowestCommonAncestor(root.right, p, q);
if(left!=null && right!=null) return root;
if(left==null) return right;
if(right==null) return left;
// 不加最后一句,leetcode无法通过编译
return null;
}
}
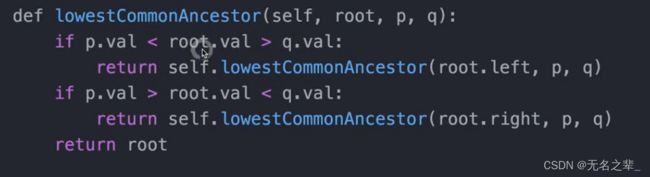
L235. 二叉搜索树的最近公共祖先
这里是二叉搜索树,可以直接用值进行判断:
一定要注意:1、边界条件;2、路径节点左右子树的递归逻辑,考虑全了
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
if(root.val == q.val || root.val == p.val || root==null) return root;
if(((q.val < root.val) && (root.val < p.val)) || ((q.val > root.val) && (root.val > p.val))){
return root;
}
else if((q.val < root.val) && (q.val < root.val)){
return lowestCommonAncestor(root.left, p, q);
}
else{
return lowestCommonAncestor(root.right, p, q);
}
}
}
L103. 二叉树的锯齿形遍历
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> ans = new ArrayList<>();
bianli(root, ans, 0);
List<List<Integer>> ans_ = new ArrayList<>();
for(int i=0;i<ans.size();i++){
ans_.add(new LinkedList<>());
if(i%2==0){
for(int j:ans.get(i)){
ans_.get(i).add(j);
}
}
else{
for(int j=ans.get(i).size()-1;j>=0;j--){
int temp = ans.get(i).get(j);
ans_.get(i).add(temp);
}
}
}
return ans_;
}
// h表明当前遍历的深度
public void bianli(TreeNode root ,List<List<Integer>> ans, int h){
if(root==null) {return;}
if(ans.size() <= h){
ans.add(new LinkedList<>());
}
ans.get(h).add(root.val);
bianli(root.left,ans,h+1);
bianli(root.right,ans,h+1);
}
}
动态规划
核心框架
1、状态转移方程
你把 f(n) 想做⼀个状态 n,这 个状态 n 是由状态 n - 1 和状态 n - 2 相加转移⽽来,这就叫状态转移
有个DP table进行计算,然后使用备忘录的手段去优化。
如何聪明地去穷举
L322 零钱兑换
使用广度递归算法,并且使用【备忘录】,回溯一定要注意递归的边界条件,明确递归函数返回值的意义
主要就是依据状态转移方程来写代码,别的别考虑那么多。

方法一:自顶向下
自顶向下主要是使用dp()函数,从amount开始,逐步向下计算
class Solution {
// 广度优先算法
public int mem[];
public int coinChange(int[] coins, int amount) {
// 备忘录
mem = new int[amount+1];
if(coins.length<=0) return -1;
return dp(coins, amount);
}
// 这里dp返回的是达到当前amount的最小“硬币数之和”
public int dp(int[] coins,int amount){
if(amount<0) return -1;
if(amount==0) return 0;
// 备忘录
if(mem[amount]!=0) return mem[amount];
// int res=-1;
int min = Integer.MAX_VALUE;
for(int coin : coins){
int res = dp(coins,amount-coin);
// 这里要考虑递归的边界条件
if ((amount-coin)>= 0 && res!=-1)
min = Math.min(min, dp(coins,amount-coin)+1);
}
// 备忘录
if(min==Integer.MAX_VALUE) mem[amount] = -1;
else mem[amount] = min;
return mem[amount];
}
}
// 解法二
import java.util.Arrays;
class Solution {
public List<Integer> memo = new ArrayList<Integer>();
public int coinChange(int[] coins, int amount) {
for (int i = 0; i < amount + 1; i++) {
memo.add(-2);
}
return dp(coins,amount);
}
public int dp(int[] coins, int amount){
if(amount<0) return -1;
if(amount==0) return 0;
if(memo.get(amount)!=-2){
return memo.get(amount);
}
int min = Integer.MAX_VALUE;
for(int coin:coins){
// 不用备忘录
int tmp = dp(coins,amount - coin);
if(tmp != -1){
min = Math.min(tmp + 1, min);
}
}
if(min==Integer.MAX_VALUE) {
memo.set(amount, -1);
return -1;
}
memo.set(amount, min);
return min;
}
}
方法二:自底向上
使用dp[]数组,从dp[1]dp[2]…dp[amount]逐渐计算出来
class Solution {
public int coinChange(int[] coins, int amount) {
int[] dp = new int[amount+1];
for(int i=0; i<amount+1;i++)
dp[i] = Integer.MAX_VALUE;
dp[0] = 0;
for(int i =0;i<amount+1;i++){
for(int coin :coins){
if(i-coin >= 0 && dp[i-coin]!=Integer.MAX_VALUE){
dp[i] = Math.min(dp[i], dp[i-coin]+1);
}
}
}
if(dp[amount]==Integer.MAX_VALUE) return -1;
return dp[amount];
}
}
L72 编辑距离
解法一:使用暴力解法会超时
//import java.lang.Math;
class Solution {
public static String w1,w2;
public static int minDistance(String word1, String word2) {
w1 = word1;
w2 = word2;
return dp(word1.length()-1,word2.length()-1);
}
public static int dp(int i,int j){
if(i==-1) return j+1;
if(j==-1) return i+1;
if (w1.charAt(i)==w2.charAt(j)){
return dp(i-1,j-1);
}
return min(dp(i-1,j)+1,
dp(i,j-1)+1,
dp(i-1,j-1)+1);
}
public static int min(int a,int b,int c){
return Math.min(Math.min(a,b),c);
}
public static void main(String[] args) {
minDistance("dinitrophenylhydrazine",
"benzalphenylhydrazone");
}
}
【参考别的地方增加一个记忆模块,进行修改】
暴力解法毫不意外的会超时,仔细想想发现,这里会对大量的[i,j]重复计算,因此需要剪枝,把已经计算过的i,j组合的结果保存起来,代码如下:
int dfs(string& word1, string& word2, int i, int j, vector<vector<int>>& memo){
if(i == word1.size()) return word2.size() - j;
if(j == word2.size()) return word1.size() - i;
if(memo[i][j] > 0) return memo[i][j];
int res = 0;
if(word1[i] == word2[j]) res = dfs(word1, word2, i + 1, j + 1, memo);
else{
int r1 = dfs(word1, word2, i + 1, j, memo); //删除word1[i]
int r2 = dfs(word1, word2, i + 1, j + 1, memo); //修改word1[i]为word2[j]
int r3 = dfs(word1, word2, i, j + 1, memo); //在i位置插入字符word2[j]
res = 1 + min(r1, min(r2, r3));
}
return memo[i][j] = res;
}
int minDistance(string word1, string word2){
vector<vector<int>> memo(word1.size(), vector<int>(word2.size(), 0));
return dfs(word1, word2, 0, 0, memo);
}
作者:hanhan13
链接:https://leetcode-cn.com/problems/edit-distance/solution/ji-zhi-qiu-jie-cong-brute-forcedao-1wei-dp-by-hanh/
解法二:用备忘录解法,二维DP使用一个二维数组进行记录
// 备忘录解法、能够优化子问题的结构重复问题
public class l72 {
public int minDistance(String word1, String word2) {
int l1 = word1.length();
int l2 = word2.length();
int [][]dp = new int[l1+1][l2+1];
//注意边界条件的值,这里dp[0][0]=0而不是1
dp[0][0]=0;
// 对dp的边界赋值
for(int i=0;i<l1;i++){
dp[i][0]=i;
}
for(int j=0;j<l2;j++){
dp[0][j] = j;
// dp[j][0]=j;
}
// 执行变量的状态转换
// i,j分别指向word1和word2
for(int i=1;i<l1;i++){
for(int j=1;j<l2;j++){
// java获取字符串某个位置的字符 charAt
if (word1.charAt(i)==word2.charAt(j)){
dp[i][j] = dp[i-1][j-1];
}
else{
dp[i][j] = min(dp[i-1][j]+1, // word2字符串增,word1删
dp[i][j-1]+1, // word1增,word2删
dp[i-1][j-1]+1 // word1/2字符串改
);
}
}
}
// 注意这里并不是返回dp[l1][l2]
return dp[l1][l2];
}
public static int min(int a,int b,int c){
return Math.min(Math.min(a,b),c);
}
public static void main(String[] args) {
}
}
数组
33. 搜索旋转排序数组
找出数组中第K大的数字:
public class l215 {
public static int findKthLargest(int[] nums, int k){
return quickSort(nums,k,0,nums.length-1);
}
private static int quickSort(int[] nums, int k, int left, int right){
int index = 4;
int flag = nums[index];
nums[index]=nums[left];
int i=left,j=right;
while(i<j){
while(i<j && nums[j]<=flag) j--;
nums[i]=nums[j];
while(i<j && nums[i]>=flag) i++;
nums[j]=nums[i];
}
nums[i]=flag;
if(i==k-1)
return nums[i];
else if(i<k-1)
return quickSort(nums, k,i+1,right);
else
return quickSort(nums, k, left, i-1);
}
public static void main(String[] args) {
int nums[] = new int[]{3,4,5,1,9,8};
findKthLargest(nums,2);
}
}
输入输出
sout System.out.println(head.val);
psvm
链表
定义
class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
JAVA虽然没有指针的概念,但是任意一个变量都是指针,在链表节点声明中尤其明显。
ListNode mainHead = new ListNode(0);
ListNode[]a = myreverse(head, tail);
// 链表反转
public static ListNode[] myreverse(ListNode head, ListNode tail){
ListNode mainHead = tail;
ListNode mainTail = head;
tail.next = null;
ListNode prev = tail.next,temp;
while (head != null){
temp = head.next;
head.next = prev;
prev = head;
head = temp;
}
return new ListNode[]{mainHead,mainTail};
}
整体做题思路
反转K个节点
头部指针不能动、哪个是运动的、定义元操作、定义前后连接指针
Java无指针概念但每个变量都是指针
LRU算法
每次最近查找的key放在队列头部,这个队列需要是有序的,如果只使用hashmap是无序的。
使用双向链表+散列表实现
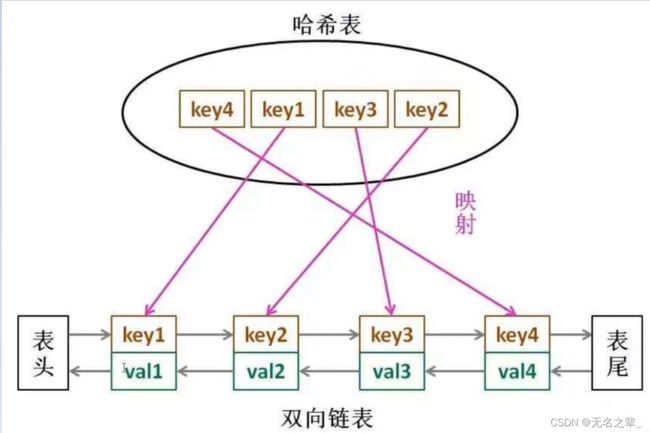
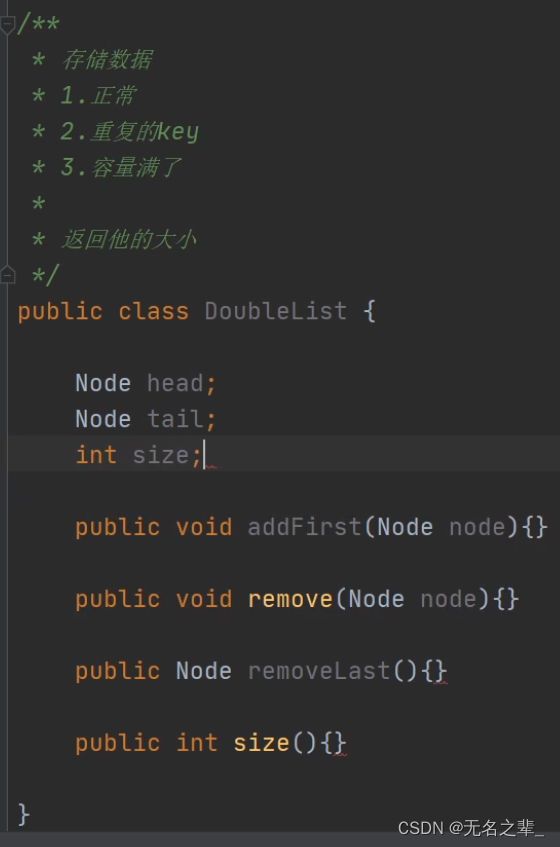
考虑几个存储数据的操作方法:
HashSet
import java.util.HashSet;
HashSet a = new HashSet();
a.add(headA);
a.contains(headB)
算法小抄阅读笔记
时间复杂度计算
递归算法的时间复杂度怎么计算?⼦问题个数乘以解决⼀个⼦问题需要的时间。
斐波那契数的计算
int fib(int N) {
if (N == 1 || N == 2) return 1;
return fib(N - 1) + fib(N - 2);
}