python百题大通关解题记录-图和树

目录

025实现二叉搜索树

挑战内容

026实现二叉树的深度优先遍历 

挑战内容

 027实现二叉树的广度优先遍历

挑战内容

028计算二叉树的高度 

挑战内容

029实现高度最小的二叉搜索树 

挑战内容

030为二叉树的每个层级创建一个列表 

挑战内容

031检查二叉树是否平衡 

挑战内容

032检查二叉树是否是搜索树 

挑战内容

033查找二叉搜索树的中序后继结点 

挑战内容

034查找二叉搜索树的第二大结点 

挑战内容

035寻找两个结点的最近共同祖先 

挑战内容

037实现最小堆 

挑战内容

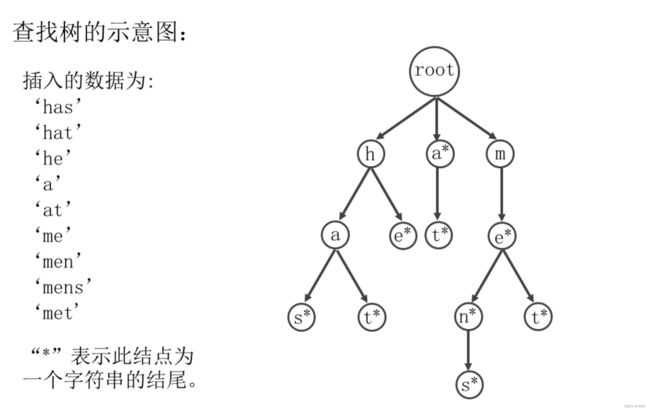
038实现查找树 

挑战内容

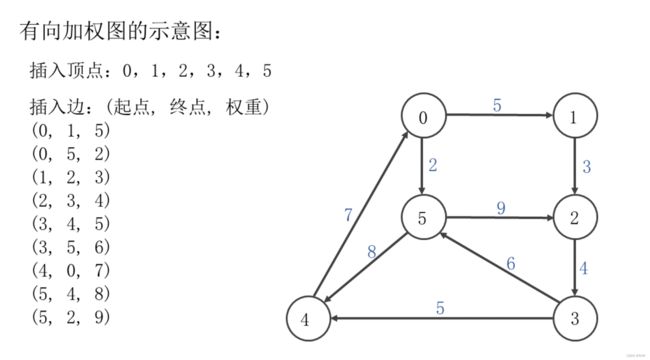
039实现图 

挑战内容

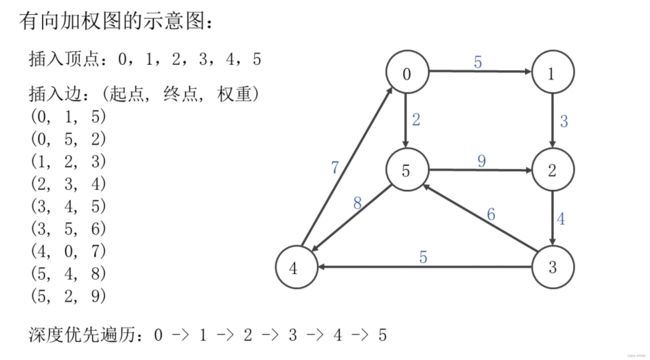
040实现图的深度优先遍历 

挑战内容

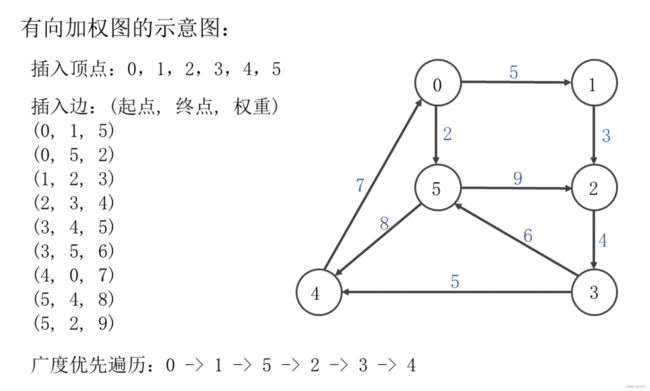
041实现图的广度优先遍历 

挑战内容

042检查图中两个顶点之间是否存在路径 

挑战内容

043在加权图中找到最短路径 

挑战内容

044在未加权图中找到最短路径 

挑战内容

---

内容编译自 Donne Martin 的开源项目

025实现二叉搜索树

实现二叉搜索树的插入方法。二叉搜索树如果不是一棵空树，则是具有下列以下性质的二叉树：

• 若它的左子树不空，则左子树上所有结点的值均小于它根结点的值；
• 若它的右子树不空，则右子树上所有结点的值均大于它根结点的值；
• 它的左、右子树也分别为二叉搜索树。

挑战内容

本次挑战中，你需要在 bst.py 文件中补充类 Node 和类 Bst 的空缺部分。

• Node 类是定义的树结点。

• Node 中的 __init__ 方法用于初始化树结点，树结点包含数据元素 data，指向左子结点的指针 left，指向右子结点的指针 right，以及指向父结点的指针 parent。

• Bst 类是定义的二叉搜索树。

• Bst 中的 __init__ 方法用于初始化二叉搜索树，参数 root 表示根结点。

• Bst 中的 insert 方法用于进行插入操作，参数 data 用于指定插入的数据元素，需要返回插入的树结点。

代码：递归

class Node(object)://树节点，包括数据，左节点，右节点，父节点

    def __init__(self, data):
        self.data=data
        self.left=None
        self.right=None
        self.parent=None

    def __repr__(self)://返回打印方法
        return str(self.data)


class Bst(object):

    def __init__(self, root=None):
        self.root=root

    def insert(self, data)://插入函数，一般需要递归，但是题目中的insert()参数量不足（少一个节点变量），且涉及返回值，递归功能放进_insert()中，
        if data is None://数据空类型
            raise TypeError('Wrong')
        if self.root is None://根节点为空
            self.root=Node(data)
            return self.root
        else://进入大小比较选择·
            return self._insert(self.root,data)

    def _insert(self,node,data):
        if node is None://注：此处无用，因为node如果为空，可直接放入数据节点，不会进入此方法
            return Node(data)
        if data<=node.data:
            if node.left is None://为空，插入节点，指定父节点，返回插入节点
                node.left=Node(data)
                node.left.parent=node
                return node.left
            else://不为空，递归，知道遇到左右为空的节点（能填充子树且满足条件的节点）
                return self._insert(node.left,data)
        else:
            if node.right is None:
                node.right=Node(data)
                node.right.parent=node
                return node.right
            else:
                return self._insert(node.right,data)

026实现二叉树的深度优先遍历 

实现二叉树的深度优先遍历，深度优先遍历方法包括中序遍历，前序遍历，后序遍历三种。深度优先遍历的介绍如下：

• 深度优先遍历是从根节点出发，沿着左子树方向进行纵向遍历，直到找到叶子节点为止。然后回溯到前一个节点，进行右子树节点的遍历，直到遍历完所有可达节点为止。
• 中序遍历：左子树 -> 根结点 -> 右子树
• 前序遍历：根结点 -> 左子树 -> 右子树
• 后序遍历：左子树 -> 右子树 -> 根结点

挑战内容

本次挑战中，你需要在 tree_dfs.py 文件中补充类 BstDfs 的空缺部分。

• BstDfs 类继承“实现二叉搜索树”挑战中的 Bst 类。
• BstDfs 中的 in_order_traversal，pre_order_traversal， post_order_traversal 方法分别用于进行中序遍历操作，前序遍历操作，后序遍历操作。
• 三个遍历函数的参数 node 表示结点，在进行遍历操作时使用根结点；参数 visit_func 是一个获取结点数据，并将结点数据添加到数组的函数。其中 visit_func 函数无需自行定义，它的参数为 node，无返回值。

 代码：

from bst import Bst


class BstDfs(Bst)://递归再递归

    def in_order_traversal(self, node, visit_func):
        if node is not None:
            self.in_order_traversal(node.left,visit_func)
            visit_func(node)
            self.in_order_traversal(node.right,visit_func)

    def pre_order_traversal(self, node, visit_func):
        if node is not None:
            visit_func(node)
            self.pre_order_traversal(node.left,visit_func)
            
            self.pre_order_traversal(node.right,visit_func)


    def post_order_traversal(self,node, visit_func):
        if node is not None:
            self.post_order_traversal(node.left,visit_func)
            
            self.post_order_traversal(node.right,visit_func)
            visit_func(node)

 027实现二叉树的广度优先遍历

实现二叉树的广度优先遍历。广度优先遍历的介绍如下：

• 广度优先遍历是从根节点出发，在横向遍历二叉树层段节点的基础上纵向遍历二叉树的层次。广度遍历即寻常所说的层次遍历。
• 层次遍历：从上到下，从左到右。

挑战内容

本次挑战中，你需要在 tree_bfs.py 文件中补充类 BstDfs 的空缺部分。

• BstDfs 类继承“实现二叉搜索树”挑战中的 Bst 类。
• BstDfs 中的 bfs 方法用于进行层次遍历操作。
• bfs 函数的参数 visit_func 是一个获取结点数据，并将结点数据添加到数组的函数。其中 visit_func 函数无需自行定义，它的参数为 node，无返回值。

代码：deque()双向队列，专业广度遍历

from bst import Bst
from collections import deque

class BstBfs(Bst):

    def bfs(self, visit_func):
        if self.root is None:
            raise TypeError('Wrong')
        queue=deque()
        queue.append(self.root)//加入队列
        while queue:
            node=queue.popleft()//左弹出，并把弹出节点遍历，加入其左右节点
            visit_func(node)
            if node.left is not None:
                queue.append(node.left)//加入队列
            if node.right is not None:
                queue.append(node.right)

028计算二叉树的高度 

实现一个算法计算二叉树的高度。树高度的介绍如下：

• 沿每个结点到根结点的唯一通路上结点的数目，称作该结点的深度。约定根节点的深度为 1。
• 树中所有节点深度的最大值称作该树的高度。空树的高度为 0。

挑战内容

本次挑战中，你需要在 tree_height.py 文件中补充类 BstHeight 的空缺部分。

• BstHeight 类继承“实现二叉搜索树”挑战中的 Bst 类。
• BstHeight 中的 height 方法用于计算树的高度。
• height 函数的参数 node 表示结点，在计算高度时使用根结点。
• height 函数需要返回一个表示树高度的数字。

代码：递归，有则加一，无则为零 

from bst import Bst


class BstHeight(Bst):

    def height(self, node):
        if node is None://空节点记0
            return 0
        return 1+max(self.height(node.left),self.height(node.right))//反复递归，每层加一，直到为空，取最大的高度

029实现高度最小的二叉搜索树 

使用排序后的数组构建高度最小的二叉搜索树。

• 对于数组 [1, 2, 3, 4, 5, 6, 7,]，构建的二叉搜索树高度为 3。

挑战内容

本次挑战中，你需要在 min_bst.py 文件中补充类 MinBst 的空缺部分。

• MinBst 中的 create_min_bst 方法用于构建二叉搜索树。
• create_min_bst 函数的参数 array 用于指定传入的数组，数组的元素按从小到大顺序排列。
• create_min_bst 函数需要返回根结点。

代码：递归，反复找中点 

from bst import Node


class MinBst(object):

    def create_min_bst(self, array):
        if array is None:
            return
        return self.mid(array,0,len(array)-1)
    def mid(self,array,start,end):
        if end

030为二叉树的每个层级创建一个列表 

为二叉搜索树的每个层级创建一个列表。介绍如下：

• 对于二叉树，将每个结点的深度记为它的层数，根结点的层为 1。
• 对于插入数据为 7 -> 9 -> 5 -> 2 -> 6 -> 11 的二叉搜索树，结果为 [[7], [5, 9], [2, 6, 11]]。

挑战内容

本次挑战中，你需要在 level_lists.py 文件中补充类 BstLevelLists 的空缺部分。

• BstLevelLists 类继承“实现二叉搜索树”挑战中的 Bst 类。
• BstLevelLists 中的 create_level_lists 方法用于为二叉搜索树的每个层级创建一个列表。
• create_level_lists 函数没有参数，需要返回一个列表。

代码：deque()方法的另一种实现方式 

from bst import Bst


class BstLevelLists(Bst):

    def create_level_lists(self):
        if self.root is None:
            return
        results=[]
        col=[]
        temp=[]
        col.append(self.root)
        while col:
            results.append(col)
            temp=list(col)
            col=[]//清空本层，进入下一层
            for parent in temp:
                if parent.left is not None:
                    col.append(parent.left)
                if parent.right is not None:
                    col.append(parent.right)
        return results

031检查二叉树是否平衡 

实现一个算法检查一个二叉树是否是平衡二叉树。平衡二叉树的介绍如下：

• 平衡二叉树要求左右两个子树的高度差绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。

挑战内容

本次挑战中，你需要在 balance_tree.py 文件中补充类 BstBalance 的空缺部分。

• BstBalance 类继承“实现二叉搜索树”挑战中的 Bst 类。
• BstBalance 中的 check_balance 方法用于检查一个二叉树是否是平衡树。
• check_balance 函数没有参数，需要返回一个布尔值，即 True 或者 False。
• 对于空树，需要使用 raise 语句显示 TypeError。

 代码：运用递归，不是平衡二叉树返回-1（用一个另类值作为标志符号），是平衡二叉树返回其深度（高度）。

from bst import Bst


class BstBalance(Bst):

    def check_balance(self)://调用方法，返回最终结果
        if self.root is None:
            raise TypeError('wrong')
        height=self.check(self.root)
        return height!=-1//除非否定符号‘-1’，否则正常高度都是自然数

    def check(self,node):
        if node is None://没有该节点返回高度0
            return 0
        left_height=self.check(node.left)
        if left_height==-1://如果等于-1，意味着左边不是平衡二叉树（diff判断是产生-1返回值的源头）
            return -1
        right_height=self.check(node.right)
        if right_height==-1://如果等于-1，意味着右边不是平衡二叉树（diff判断是产生-1返回值的源头）
            return -1
        diff=abs(left_height-right_height)
        if diff>1://源自定义的判断，-1仅代表一个否定符号
            return -1
        return 1+max(left_height,right_height)//正经的平衡二叉树，返回其高度，根节点加上子树最大高度

032检查二叉树是否是搜索树 

实现一个算法检查一个二叉树是否是二叉搜索树。

挑战内容

本次挑战中，你需要在 tree_validate.py 文件中补充类 BstValidate 的空缺部分。

• BstValidate 类继承“实现二叉搜索树”挑战中的 Bst 类。
• BstValidate 中的 validate 方法用于检查一个二叉树是否是二叉搜索树。
• validate 函数没有参数，需要返回一个布尔值，即 True 或者 False。
• 对于空树，需要使用 raise 语句显示 TypeError。

代码：递归，检验左右节点数据是否满足要求。注意：二叉搜索树是没有重复数据的 

from bst import Bst
import sys

class BstValidate(Bst):

    def validate(self):
        if self.root is None:
            raise TypeError('d')
        return self._check(self.root)

    def _check(self,node,minimum=-sys.maxsize,maximum=sys.maxsize):
        if node is None://结束时，节点为空，符合，运用于第三四个if判断
            return True
        if node.datamaximum://数据超出范围，不符合
            return False
        if not self._check(node.left,minimum,node.data)://左节点检测，上限为父节点数据
            return False
        if not self._check(node.right,node.data,maximum)://右节点检测，下限为父节点数据
            return False
        return True//叶子结点，数据不超过范围，符合

033查找二叉搜索树的中序后继结点 

实现一个算法查找二叉搜索树某节点的中序后继结点。某节点的中序后继结点指的是，对二叉搜索树进行中序遍历时，此节点的后面一个结点。

挑战内容

本次挑战中，你需要在 tree_next.py 文件中补充类 BstSuccessor 的空缺部分。

• BstSuccessor 中的 get_next 方法用于查找二叉搜索树某节点的中序后继结点。
• get_next 函数的参数 node 用于指定要查找的结点。
• get_next 函数需要返回后继结点的数据元素。
• 如果指定的结点为中序遍历的最后一个结点，则返回 None。
• 对于空树，需要使用 raise 语句显示 TypeError。

代码：中序后继节点分两类：向上找父节点，向下找子节点

from bst import Node


class BstSuccessor(object):

    def get_next(self, node):
        if node is None:
            raise TypeError
        if node.right is None:
            return self.nextancestor(node)
        else:
            return self.nextchild(node.right)

    def nextchild(self,node):
        if node.left is None:
            return node.data
        else:
            return self.nextchild(node.left)

    def nextancestor(self,node):
        if node.parent is not None:
            if node.parent.data

034查找二叉搜索树的第二大结点 

实现一个算法查找二叉搜索树中结点数据第二大的结点。

挑战内容

本次挑战中，你需要在 second_largest.py 文件中补充类 Solution 的空缺部分。

• Solution 类继承“实现二叉搜索树”挑战中的 Bst 类。
• Solution 中的 find_second_largest 方法用于查找二叉搜索树中结点数据第二大的结点。
• find_second_largest 函数的没有参数，需要返回一个结点。
• 对于空树，需要使用 raise 语句显示 TypeError。
• 对于只有一个结点的树，需要使用 raise 语句显示 ValueError。

 代码：第二大节点有三种状况：1.左右节点都有。2.只有右节点。3.只有左节点。1和2先找到最右侧最底端的树，最大值是右侧叶子结点，第二大是紧挨的父节点；3的最大节点是根节点（最上面的），第二大节点是左子树最大的节点。

from bst import Bst


class Solution(Bst):

    def find_second_largest(self)://输出函数
        if self.root is None:
            raise TypeError
        if self.root.right is None and self.root.left is None:
            raise ValueError
        return self.find(self.root)

    def find(self,node)://主要功能函数
        if node.right is not None://存在右节点。如果它不是叶子结点，对其递归寻找；如果是叶子节点，返回node，结束递归
            if node.right.left is not None or node.right.right is not None:
                return self.find(node.right)
            else:
                return node
        else://不存在右节点，返回左子树最大值
            return self.findmost(node.left)

    def findmost(self,node)://辅助函数，为左子树寻最大值
        if node.right is not None:
            return self.findmost(node.right)
        else:
            return node

035寻找两个结点的最近共同祖先 

实现一个算法查找二叉树中两个结点的最近共同祖先。最近共同祖先的介绍如下：

• 最近公共祖先是指当给定一个有根树 T 时，对于任意两个结点 u、 v，找到一个离根最远的结点 x，使得 x 同时是 u 和 v 的祖先，x 便是 u、 v 的最近公共祖先。

挑战内容

本次挑战中，你需要在 tree_lca.py 文件中补充类 BinaryTree 的空缺部分。

• BinaryTree 中的 lca 方法用于查找二叉树中两个结点的最近共同祖先。
• lca 函数的参数 root 指根节点，node1 和 node2 用于指定要查找的两个结点。
• lca 函数需要返回一个结点。
• 对于空树，需要返回 None。
• 如果要查找的结点不在树中，也需要返回 None。

 代码：复杂递归

class Node(object):

    def __init__(self, key, left=None, right=None):
        self.key = key
        self.left = left
        self.right = right

    def __repr__(self):
        return str(self.key)


class BinaryTree(object):

    def lca(self, root, node1, node2)://主函数，非空判断+节点存在检测+寻找最近共祖
        if None in (root,node1,node2):
            return None
        if self.check(root,node1) or self.check(root,node2):
            return None
        return self.find(root,node1,node2)

    def check(self,root,node)://节点存在检测：方法是左右节点向下递归直到root代表的节点就是node节点，如果不是则递归到root代表的节点为空。递归过程中只要检测到存在就赋值False。不存在输出True，存在输出False
        if root is None:
            return True
        if root is node:
            return False
        left=self.check(root.left,node)
        right=self.check(root.right,node)
        return left and right

    def find(self,root,node1,node2)://最近共祖寻找：方法是左右节点向下递归：root代表的节点为空，返回空；root一旦是node1或者node2，返回该节点；左右子树分别向下递归寻找，都不为空则两节点分布在该数两侧，返回该树根节点为最近共祖，否则选择为空的那一侧的返回点
        if root is None:
            return None
        if root is node1 or root is node2:
            return root
        left_node=self.find(root.left,node1,node2)
        right_node=self.find(root.right,node1,node2)
        if left_node is not None and right_node is not None:
            return root
        else:
            return left_node if left_node is not None else right_node

037实现最小堆 

实现最小堆插入，查看最小元素，删除最小元素的方法。最小堆排序的介绍如下：

• 堆一般用完全二叉树来实现。
• 完全二叉树是指对于深度为 h 的二叉树，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边。
• 最小堆是指对于一个完全二叉树，所有的结点（叶子结点除外）的值都小于其左右子结点的值。
• 堆排序是指由无序序列生成堆。
• 最小堆用一个数组以层序遍历的方式存储，子节点索引与父节点索引有（2n+1）（2n+2）的关系
• 插入是在末尾加入一个节点，由此节点向上调整堆
• 删除是弹出开头元素，把最后一个元素放置在开头，然后向下调整  

挑战内容

本次挑战中，你需要在 min_heap.py 文件中补充类 MinHeap 的空缺部分。

• MinHeap 类是定义的最小堆。
• MinHeap 中的 __init__ 方法用于初始化。
• MinHeap 中的 __len__ 方法用于返回最小堆元素个数。
• MinHeap 中的 extract_min 方法用于删除最小堆中的最小元素，在删除最小元素后，需要进行向下调整排序使得它也是最小堆。它没有参数，需要返回删除的元素值。如果最小堆为空，则返回 None。
• MinHeap 中的 peek_min 方法用于查看最小堆中的最小元素。它没有参数，需要返回最小的元素值。如果最小堆为空，则返回 None。
• MinHeap 中的 insert 方法用于进行插入操作，在插入元素后，需要向上调整排序使得它也是最小堆。参数 data 用于指定插入的数据元素，它没有返回值。如果传入的 data 为 None，需要使用 raise 语句显示 TypeError。
• MinHeap 中的 _bubble_up 为类的私有方法，它用于在插入时进行向上调整排序。参数 index 用于指定数组的索引，它没有返回值。
• MinHeap 中的 _bubble_down 为类的私有方法，它用于在删除时进行向下调整排序。参数 index 用于指定数组的索引，它没有返回值。

 代码：向上调整只需要比较父节点，向下调整需要和最小的子节点比较

class MinHeap(object):

    def __init__(self):
        self.array = []

    def __len__(self):
        return len(self.array)

    def extract_min(self):
        if not self.array:
            return None
        if len(self.array)==1:
            return self.array.pop(0)
        minimum=self.array[0]
        #移动最后一个元素到根节点
        self.array[0]=self.array.pop(-1)
        self._bubble_down(index=0)
        return minimum

    def peek_min(self):
        return self.array[0] if self.array else None

    def insert(self, data):
        if data is None:
            raise TypeError
        self.array.append(data)
        self._bubble_up(index=len(self.array)-1)

    def _bubble_up(self, index):
        if index==0:
            return
        index_parent=(index-1)//2
        if self.array[index]self.array[min_index]:
            self.array[index],self.array[min_index]=self.array[min_index],self.array[index]
        self._bubble_down(min_index)

    def _find_smaller_child(self,index)://辅助寻找最小子节点
        left_index=2*index+1
        right_index=2*index+2
        #没有右孩子
        if right_index>=len(self.array):
            #更没有左孩子
            if left_index>=len(self.array):
                return -1
            else:
                return left_index
        else:
            return left_index if self.array[left_index]

038实现查找树 

实现查找树查找，插入，删除，列出元素的方法。查找树的介绍如下：

• 根结点不包含字符，除根结点外每一个结点都只包含一个字符；
• 从根结点到某一结点，路径上经过的字符连接起来，为该结点对应的字符串；
• 每个结点的所有子结点包含的字符都不相同。

  

挑战内容

本次挑战中，你需要在 trie.py 文件中补充类 Node 和类 Trie 的空缺部分。

• Node 类是定义的查找树结点。

• Node 中的 __init__ 方法用于初始化查找树结点。结点包含数据元素 data，指向父结点的指针 parent，表示此结点是否为字符串结尾的布尔值 terminates，以及此结点的子结点 children。其中子结点 children 为字典形式，字典的键为该子结点的字符，值为该子结点的结点。

• Trie 类是定义的查找树。

• Trie 中的 __init__ 方法用于初始化，包含根结点 root。

• Trie 中的 find 方法用于进行查找操作。它的参数 word 用于指定要查找的字符串，需要返回此字符串结尾的结点。如果找不到此字符串，需要返回 None。如果查找的字符串为 None，需要使用 raise 语句显示 TypeError。

• Trie 中的 insert 方法用于进行插入操作。它的参数 word 用于指定要插入的字符串，没有返回值。如果插入的字符串为 None，需要使用 raise 语句显示 TypeError。

• Trie 中的 remove 方法用于进行删除操作。它的参数 word 用于指定要删除的字符串，没有返回值。如果要删除的字符串为 None，需要使用 raise 语句显示 TypeError。如果要删除的字符串不存在，需要使用 raise 语句显示 KeyError。

• Trie 中的 list_words 方法用于进行列出查找树里的所有字符串，它没有参数，需要返回包含字符串的数组。

代码：学习列出所有字符串的方法

from collections import OrderedDict


class Node(object):

    def __init__(self, data, parent=None, terminates=False):
        self.data=data
        self.terminates=False
        self.parent=parent
        self.children={}


class Trie(object):

    def __init__(self):
        self.root=Node('')

    def find(self, word):
        if word is None:
            raise TypeError
        node=self.root
        for char in word:
            if char in node.children:
                node=node.children[char]
            else:
                return None
        return node if node.terminates else None

    def insert(self, word):
        if word is None:
            raise TypeError
        node=self.root
        parent=None
        for char in word:
            if char in node.children:
                node=node.children[char]
            else:
                node.children[char]=Node(char,parent=node)
                node=node.children[char]
        node.terminates=True 

    def remove(self, word):
        if word is None:
            raise TypeError
        node=self.find(word)
        if node is None:
            raise KeyError
        node.terminates=False
        parent=node.parent
        while parent is not None:
            if node.children:
                return
            del node
            node=parent
            parent=parent.parent

    def list_words(self)://主方法，负责调用返回
        result=[]
        curr_word=''
        self._list_words(self.root,curr_word,result)
        return result

    def _list_words(self,node,curr_word,result)://功能函数
        if node is None:
            return
        for data,child in node.children.items()://数据和节点同时遍历
            if child.terminates://到达末尾，加上遍历得到的word
                result.append(curr_word+data)
            self._list_words(child,curr_word+data,result)

039实现图 

实现图插入顶点，插入有向加权边，插入无向加权边的方法。图的介绍如下：

• 图是一些顶点的集合，这些顶点通过一系列边连接。
• 边可以有权重，每一条边可以被分配一个数值作为边的权重。
• 边可以是没有方向的，称为无向图。边也可以是有方向的，称为有向图。
• 顶点的度是指和该顶点相连的边的条数。对于无向图，顶点的度就是和此顶点相连接的边的条数。对于有向图，顶点的度分为入度和出度。其中顶点的出边条数称为该顶点的出度，顶点的入边条数称为该顶点的入度。

挑战内容

本次挑战中，你需要在 graph.py 文件中补充类 Node 和类 Trie 的空缺部分。

• Node 类是定义的顶点。

• Node 中的 __init__ 方法用于初始化顶点。顶点包含数据元素 key，表示状态的布尔值 visit_state，表示入度的数值 incoming_edges，表示顶点的字典 adj_nodes，表示边的字典 adj_weights。其中 adj_nodes 的键为数据元素，值为顶点。而 adj_weights 的键为数据元素，值为权重。

• Node 中的 __repr__ 方法用于打印顶点的数据元素。

• Node 中的 __lt__ 方法用于比较顶点的数据元素。

• Node 中的 add_neighbor 方法用于增加顶点间的连接。参数 neighbor 用于指定相连的顶点，参数 weight 用于指定边的权重。如果 neighbor 或者 weight 为 None，需要使用 raise 语句显示 TypeError。

• Node 中的 remove_neighbor 方法用于删除顶点间的连接。参数 neighbor 用于指定相连的顶点。如果 neighbor 为 None，需要使用 raise 语句显示 TypeError。如果 neighbor 不是相连的顶点，需要使用 raise 语句显示 KeyError。

• Trie 类是定义的图。

• Trie 中的 __init__ 方法用于初始化，包含顶点 nodes。其中 nodes 为字典格式，字典的键为数据元素，字典的值为顶点。

• Trie 中的 add_node 方法用于增加顶点。参数 key 用于指定顶点的数据元素。如果 key 为 None，需要使用 raise 语句显示 TypeError。

• Trie 中的 add_edge 方法用于增加有向边。参数 source 用于指定起始顶点的数据元素，参数 dest 用于指定终点的数据元素，参数 weight 用于指定边的权重。如果 source 或者 dest 为 None，需要使用 raise 语句显示 TypeError。如果 source 或者 dest 不在已有的顶点中，需要使用数据元素创建结点后再增加边。

• Trie 中的 add_undirected_edge 方法用于增加无向边，增加无向边可认为是增加双向的有向边。参数 source 和 dest 分别用于指定两个顶点的数据元素，参数 weight 用于指定边的权重。如果 source 或者 dest 为 None，需要使用 raise 语句显示 TypeError。如果 source 或者 dest 不在已有的结点中，需要使用数据元素创建结点后再增加边。

代码：综合性的实现

from enum import Enum


class State(Enum):

    unvisited = 0
    visiting = 1
    visited = 2


class Node:

    def __init__(self, key):
        self.key = key
        self.visit_state = State.unvisited
        self.incoming_edges = 0
        self.adj_nodes = {}  # Key = key, val = Node
        self.adj_weights = {}  # Key = key, val = weight

    def __repr__(self):
        return str(self.key)

    def __lt__(self, other):
        return self.key < other.key

    def add_neighbor(self, neighbor, weight=0):
        if neighbor is None or weight is None:
            raise TypeError('neighbor or weight cannot be None')
        neighbor.incoming_edges += 1
        self.adj_weights[neighbor.key] = weight
        self.adj_nodes[neighbor.key] = neighbor

    def remove_neighbor(self, neighbor):
        if neighbor is None:
            raise TypeError('neighbor cannot be None')
        if neighbor.key not in self.adj_nodes:
            raise KeyError('neighbor not found')
        neighbor.incoming_edges -= 1
        del self.adj_weights[neighbor.key]
        del self.adj_nodes[neighbor.key]


class Graph:

    def __init__(self):
        self.nodes = {}  # Key = key, val = Node

    def add_node(self, key):
        if key is None:
            raise TypeError('key cannot be None')
        if key not in self.nodes:
            self.nodes[key] = Node(key)
        return self.nodes[key]

    def add_edge(self, source, dest, weight=0):
        if source is None or dest is None:
            raise KeyError('Invalid key')
        if source not in self.nodes:
            self.add_node(source)
        if dest not in self.nodes:
            self.add_node(dest)
        self.nodes[source].add_neighbor(self.nodes[dest], weight)

    def add_undirected_edge(self, source, dest, weight=0):
        if source is None or dest is None:
            raise TypeError('key cannot be None')
        self.add_edge(source, dest, weight)
        self.add_edge(dest, source, weight)

040实现图的深度优先遍历 

实现图的深度优先遍历方法。图的深度优先遍历介绍如下：

• 首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边走到未访问过的顶点，其中选择时依照边的添加顺序依次选择。
• 当没有未访问过的顶点时，则回到上一个顶点，继续试探别的顶点，直至所有的顶点都被访问过。

挑战内容

本次挑战中，你需要在 graph_dfs.py 文件中补充类 GraphDfs 的空缺部分。

• GraphDfs 类继承“实现图”挑战中的 Graph 类。
• GraphDfs 中的 dfs 方法用于进行深度优先遍历操作。
• dfs 函数的参数 root 表示起始顶点，参数 visit_func 是一个获取顶点数据，并将顶点数据添加到数组的函数。其中 visit_func 函数无需自行定义，它的参数为 node，无返回值。

代码：像树的深度遍历一样，对子节点遍历时进行自调用递归 

from graph import Graph,State


class GraphDfs(Graph):

    def dfs(self, root, visit_func):
        if root is None:
            return 
        visit_func(root)
        root.visit_state=State.visited
        for node in root.adj_nodes.values():
            if node.visit_state==State.unvisited:
                self.dfs(node,visit_func)

041实现图的广度优先遍历 

实现图的广度优先遍历方法。图的广度优先遍历介绍如下：

• 首先以一个未被访问过的顶点作为起始顶点，沿当前顶点的边依次坊问与它相连并且未访问过的顶点，坊问顺序为边的添加顺序。
• 当没有未访问过的顶点时，则依次以相连顶点作为起始顶点，再依次坊问它的相连顶点，直至所有的顶点都被访问过。

挑战内容

本次挑战中，你需要在 graph_bfs.py 文件中补充类 GraphBfs 的空缺部分。

• GraphBfs 类继承“实现图”挑战中的 Graph 类。
• GraphBfs 中的 bfs 方法用于进行广度优先遍历操作。
• dfs 函数的参数 root 表示起始顶点，参数 visit_func 是一个获取顶点数据，并将顶点数据添加到数组的函数。其中 visit_func 函数无需自行定义，它的参数为 node，无返回值。

 代码：类似树的广度优先遍历，遍历，使用队列一层层插入弹出

from graph import Graph, State
from collections import deque


class GraphBfs(Graph):

    def bfs(self, root, visit_func):
        if root is None:
            return
        queue = deque()
        queue.append(root)
        root.visit_state = State.visited
        while queue:
            node = queue.popleft()
            visit_func(node)
            for adjacent_node in node.adj_nodes.values():
                if adjacent_node.visit_state == State.unvisited:
                    queue.append(adjacent_node)
                    adjacent_node.visit_state = State.visited

042检查图中两个顶点之间是否存在路径 

实现一个算法来检查图中两个顶点之间是否存在路径。

挑战内容

本次挑战中，你需要在 graph_path.py 文件中补充类 GraphPathExists 的空缺部分。

• GraphPathExists 类继承“实现图”挑战中的 Graph 类。
• GraphPathExists 中的 path_exists 方法用于检查图中两个顶点之间是否存在路径。
• path_exists 函数的参数 start 和 end 分别用于指定起始顶点和结束顶点。
• path_exists 函数的需要返回一个布尔值，即 True 或者 False。
• 当传入的 start 和 end 为相同顶点时，需要返回 True。
• 当传入的 start 和 end 中有 None 时，需要返回 False。

代码：本类路径问题运用广度优先遍历进行搜索 

from graph import Graph, State
from collections import deque


class GraphPathExists(Graph):

    def path_exists(self, start, end):
        if start is None or end is None:
            return False
        if start is end:
            return True
        queue = deque()
        queue.append(start)
        start.visit_state = State.visited
        while queue:
            node = queue.popleft()
            if node is end:
                return True
            for adj_node in node.adj_nodes.values():
                if adj_node.visit_state == State.unvisited:
                    queue.append(adj_node)
                    adj_node.visit_state = State.visited
        return False

043在加权图中找到最短路径 

实现一个算法来查找有向加权图中两个顶点之间的最短路径。

挑战内容

本次挑战中，你需要在 shortest_path.py 文件中补充类 ShortestPath 的空缺部分。

• ShortestPath 中的 __init__ 方法用于初始化，需要包含属性 graph 和 path_weight。另外的属性可根据需要进行添加。

• 初始化的参数为 graph，是一个有向加权图。

• 属性 graph 是传入的有向加权图。当传入的 graph 为 None 时，需要使用 raise 语句显示 TypeError。

• 属性 path_weight 为字典形式，键为顶点，值为初始顶点到该顶点的最短路径的权值和，其中初始顶点的值为 0。

• ShortestPath 中的 shortest_path 方法用于查找有向加权图中两个顶点之间的最短路径。

• shortest_path 函数的参数 start_node_key 和 end_node_key 分别用于指定起始顶点的数据元素和结束顶点的数据元素。

• shortest_path 函数的需要返回一个数组，数组包含路径的数据元素，路径需要包含起始顶点和结束顶点。

• 如果 start_node_key 或者 end_node_key 为 None，需要使用 raise 语句显示 TypeError。

• 如果 start_node_key 或者 end_node_key 不在已有的结点中，需要使用 raise 语句显示 ValueError。

代码：比较复杂，没看懂 

import sys


class ShortestPath(object):

    def __init__(self, graph):
        if graph is None:
            raise TypeError('graph cannot be None')
        self.graph = graph
        self.previous = {}  # Key: node key, val: prev node key, shortest path
        self.path_weight = {}  # Key: node key, val: weight, shortest path
        self.remaining = PriorityQueue()  # Queue of node key, path weight
        for key in self.graph.nodes.keys():
            # Set each node's previous node key to None
            # Set each node's shortest path weight to infinity
            # Add each node's shortest path weight to the priority queue
            self.previous[key] = None
            self.path_weight[key] = sys.maxsize
            self.remaining.insert(
                PriorityQueueNode(key, self.path_weight[key]))

    def find_shortest_path(self, start_node_key, end_node_key):
        if start_node_key is None or end_node_key is None:
            raise TypeError('Input node keys cannot be None')
        if (start_node_key not in self.graph.nodes or
                end_node_key not in self.graph.nodes):
            raise ValueError('Invalid start or end node key')
        # Set the start node's shortest path weight to 0
        # and update the value in the priority queue
        self.path_weight[start_node_key] = 0
        self.remaining.decrease_key(start_node_key, 0)
        while self.remaining:
            # Extract the min node (node with minimum path weight)
            # from the priority queue
            min_node_key = self.remaining.extract_min().obj
            min_node = self.graph.nodes[min_node_key]
            # Loop through each adjacent node in the min node
            for adj_key in min_node.adj_nodes.keys():
                # Node's path:
                # Adjacent node's edge weight + the min node's
                # shortest path weight
                new_weight = (min_node.adj_weights[adj_key] +
                    self.path_weight[min_node_key])
                # Only update if the newly calculated path is
                # less than the existing node's shortest path
                if self.path_weight[adj_key] > new_weight:
                    # Set the node's previous node key leading to the shortest path
                    # Update the adjacent node's shortest path and
                    # update the value in the priority queue
                    self.previous[adj_key] = min_node_key
                    self.path_weight[adj_key] = new_weight
                    self.remaining.decrease_key(adj_key, new_weight)
        # Walk backwards to determine the shortest path:
        # Start at the end node, walk the previous dict to get to the start node
        result = []
        current_node_key = end_node_key
        while current_node_key is not None:
            result.append(current_node_key)
            current_node_key = self.previous[current_node_key]
        # Reverse the list
        return result[::-1]


# 挑战24的参考答案
class PriorityQueueNode(object):

    def __init__(self, obj, key):
        self.obj = obj
        self.key = key

    def __repr__(self):
        return str(self.obj) + ': ' + str(self.key)


class PriorityQueue(object):

    def __init__(self):
        self.array = []

    def __len__(self):
        return len(self.array)

    def insert(self, node):
        self.array.append(node)
        return self.array[-1]

    def extract_min(self):
        if not self.array:
            return None
        minimum = sys.maxsize
        for index, node in enumerate(self.array):
            if node.key < minimum:
                minimum = node.key
                minimum_index = index
        return self.array.pop(minimum_index)

    def decrease_key(self, obj, new_key):
        for node in self.array:
            if node.obj is obj:
                node.key = new_key
                return node

044在未加权图中找到最短路径 

实现一个算法来查找未加权图中两个顶点之间的最短路径。

挑战内容

本次挑战中，你需要在 sp_unweighted.py 文件中补充类 GraphShortestPath 的空缺部分。

• GraphShortestPath 类继承“实现图”挑战中的 Graph 类。
• GraphShortestPath 中的 shortest_path 方法用于查找有向未加权图中两个顶点之间的最短路径。
• shortest_path 函数的参数 source_key 和 dest_key 分别用于指定起始顶点的数据元素和结束顶点的数据元素。
• shortest_path 函数的需要返回一个数组，数组包含路径的数据元素，路径需要包含起始顶点和结束顶点。 如果起始顶点和结束顶点为相同顶点，数组只需要包含一个元素。
• 如果 start_node_key 或者 end_node_key 为 None，则返回 None。
• 如果 start_node_key 和 end_node_key 之间没有路径，也返回 None。

 代码：

from graph import Graph, State
from collections import deque


class GraphShortestPath(Graph):

    def shortest_path(self, source_key, dest_key):
        if source_key is None or dest_key is None:
            return None
        if source_key is dest_key:
            return [source_key]
        prev_node_keys = self._shortest_path(source_key, dest_key)
        if prev_node_keys is None:
            return None
        else:
            path_ids = [dest_key]
            prev_node_key = prev_node_keys[dest_key]
            while prev_node_key is not None:
                path_ids.append(prev_node_key)
                prev_node_key = prev_node_keys[prev_node_key]
            return path_ids[::-1]

    def _shortest_path(self, source_key, dest_key):
        queue = deque()
        queue.append(self.nodes[source_key])
        prev_node_keys = {source_key: None}
        self.nodes[source_key].visit_state = State.visited
        while queue:
            node = queue.popleft()
            if node.key is dest_key:
                return prev_node_keys
            # prev_node = node
            for adj_node in node.adj_nodes.values():
                if adj_node.visit_state == State.unvisited:
                    queue.append(adj_node)
                    prev_node_keys[adj_node.key] = node.key
                    adj_node.visit_state = State.visited
        return None