数据结构算法——滑动窗口问题（以LeetCode滑动窗口题为例）

1. 滑动窗口

        滑动窗口算法是在给定特定窗口大小的数组或字符串上执行要求的操作，它的原理与网络传输TCP协议中的滑动窗口协议（Sliding Window Protocol）基本一致。

        这种技术可以将一部分问题中的嵌套循环转变为一个单循环，因此它可以减少时间复杂度。滑动窗口主要应用在数组和字符串上。

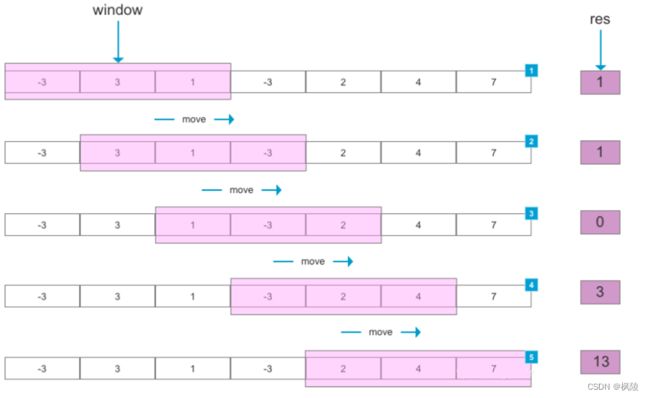
        例如，设定滑动窗口（window）大小为 3，当滑动窗口每次划过数组时，计算当前滑动窗口中元素的和，可以得到一组结果 res。

        因为滑动窗口是靠窗口起始、结束两个位置来表示的，所以滑动窗口也可以看作特殊的“双指针”。 

2. 滑动窗口最大值

力扣https://leetcode.cn/problems/sliding-window-maximum/

2.1 题目描述

        给你一个整数数组 nums，有一个大小为 k 的滑动窗口从数组的最左侧移动到数组的最右侧。你只可以看到在滑动窗口内的 k 个数字。滑动窗口每次只向右移动一位。

        返回 滑动窗口中的最大值 。

示例：

2.2 解决方法

2.2.1 暴力法

        遍历每个滑动窗口，找到每个窗口的最大值。

public class SlingWindowMax1 {
    public int[] maxSlidingWindow(int[] nums, int k){
        //定义最终结果数组
        int[] res = new int[nums.length-k+1];

        for (int i=0;i<= nums.length-k;i++){
            int max = nums[i];
            for (int j = i ; j < i+k;j++){
                if(nums[j]>max){
                    max = nums[j];
                }
            }
            res[i] = max;
        }
        return  res;
    }

    public static void main(String[] args) {
        int[] nums={1,3,-1,-3,5,3,6,7};
        SlingWindowMax1 slingWindowMax = new SlingWindowMax1();
        int[] res = slingWindowMax.maxSlidingWindow(nums, 3);
        for (int re : res) {
            System.out.print(re+"\t");
        }
    }
}

 复杂度分析

        时间复杂度： O(Nk)，双重循环，外层遍历数组循环N次，内层遍历窗口循环k次，所以整体就是O(N) * O(k) = O(Nk)，表现较差。在leetcode上提交，会发现超出了题目要求的运行时间限制。

        空间复杂度：O(N-k)，输出数组用到了N-k+1的空间。

2.2.2 双端队列法

        窗口在滑动过程中，其实数据发生的变化很小：只有第一个元素被删除、后面又新增一个元素，中间的大量元素是不变的。也就是说，前后两个窗口中，有大量数据是重叠的。

        可以使用一个队列来保存窗口数据：窗口每次滑动，我们就让后面的一个元素进队，并且让第一个元素出队。进出队列的操作，只要耗费常数时间。

        这种场景，可以使用双向队列（也叫双端队列Dequeue），该数据结构可以从两端以常数时间压入/弹出元素。在构建双向队列的时候，可以采用删除队尾更小元素的策略，所以，得到的其实就是一个从大到小排序的队列。这样存储元素，可以认为是遵循“更新更大”原则。

public class SlingWindowMax2 {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if (k == 1) {
            return nums;
        }
        int[] res = new int[nums.length - k + 1];
        ArrayDeque deque = new ArrayDeque<>();
        //初始化双端队列
        for (int i = 0; i < k; i++) {
            while (!deque.isEmpty() && nums[i] > nums[deque.getLast()]) {
                deque.removeLast();
            }
            deque.addLast(i);
        }
        res[0] = nums[deque.getFirst()];
        //遍历后续数组
        for (int i = k; i < nums.length; i++) {
            //当超出范围时，删除队列中仍保留的上一组的最大值
            if(!deque.isEmpty() && deque.getFirst() == i-k){
                deque.removeFirst();
            }
            while (!deque.isEmpty() && nums[i] > nums[deque.getLast()]){
                deque.removeLast();
            }
            deque.addLast(i);
            res[i-k+1] = nums[deque.getFirst()];
        }

        return res;
    }

    public static void main(String[] args) {
        int[] nums = {1, 3, -1, -3, 5, 3, 6, 7};
        SlingWindowMax2 slingWindowMax = new SlingWindowMax2();
        int[] res = slingWindowMax.maxSlidingWindow(nums, 3);
        for (int re : res) {
            System.out.print(re + "\t");
        }
    }
}

复杂度分析

        时间复杂度：O(N)，每个元素被处理两次：其索引被添加到双向队列中，以及被双向队列删除。

        空间复杂度： O(N)，输出数组使用了 O(N−k+1) 空间，双向队列使用了O(k)。

3. 最小覆盖子串

力扣https://leetcode.cn/problems/minimum-window-substring/

3.1 问题描述

        给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

        对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
        如果 s 中存在这样的子串，我们保证它是唯一的答案。

输入：s = "ADOBECODEBANC", t = "ABC"

输出： "BANC"

3.2 解决方法

        所谓“子串”，指的是字符串中连续的一部分字符集合。要求考察的所有字符，应该在同一个“窗口”内，这样的问题非常适合用滑动窗口的思路来解决。而所谓的“最小子串”，当然就是符合要求的、长度最小的子串了。

3.2.1 暴力法

        直接枚举出当前字符串长度大于等于t的子串，然后一一进行比对，选出覆盖T中所有字符的最小的那个。

        判断一个子串中包含了t中的所有字符：统计t每个字符出现的次数，然后在子串中进行比较。

        子串s符合要求的条件是：统计t中每个字符出现的次数，全部小于等于在s中出现次数。

public class MinimumWindowSubstring1 {
    public String minWindow(String s, String t){
        String minSub = "";
        HashMap tCount = new HashMap<>();
        for (int i = 0; i < t.length(); i++) {
            char c = t.charAt(i);
            int count = tCount.getOrDefault(c,0);
            tCount.put(c,count+1);
        }
        for (int i = 0; i < s.length(); i++) {
            for (int j = i+t.length();j<=s.length();j++){
                HashMap subCount = new HashMap<>();
                for (int k=i;k tCount,HashMap subCount){
        for (Character character : tCount.keySet()) {
            if(subCount.getOrDefault(character,0)

复杂度分析

        时间复杂度：O(|s|^3)，应该写作O(|s|^3+|t|)，这里|s|表示字符串s的长度，|t|表示t的长度。枚举s所有的子串，之后又要对每一个子串统计字符频次，所以是三重循环，耗费O(|s|^3)。另外还需要遍历t统计字符频次，耗费O(|t|)。t的长度本身要小于s，而且本题的应用场景一般情况是关键字的全文搜索，t相当于关键字，长度应该远小于s，所以可以忽略不计。

        空间复杂度：O(C)，这里C表示字符集的大小。我们用到了HashMap来存储S和T的字符频次，而每张哈希表中存储的键值对不会超过字符集的大小。

3.2.2 滑动窗口

        在暴力求解的时候，做了很多无用的比对：对于字符串“ADOBECODEBANC”，当找到一个符合条件的子串“ADOBEC”后，我们会继续仍以“A”作为起点扩展这个子串，得到一个符合条件的“ADOBECO”——它肯定符合条件，也肯定比之前的子串长，这其实是完全不必要的。

        采用滑动窗口，定义左右两个指针，每次左指针或右指针做了一次右移，只涉及到一个字符的增减。

左指针右移和右指针右移两种情况讨论：

        左指针left右移（left –> left+1）。这时子串长度减小，减少的一个字符就是s[left]，对应频次减1

        右指针right右移（right –> right+1）。这时子串长度增加，增加的一个字符就是s[right]，对应频次加1

public class MinimumWindowSubstring2 {
    public String minWindow(String s, String t){
        if (s.length() < t.length()) return "";
        String minSub = "";
        //统计所需字符及数量
        HashMap  tCount = new HashMap<>();
        for (int i = 0; i < t.length(); i++) {
            char c = t.charAt(i);
            tCount.put(c,tCount.getOrDefault(c,0)+1);
        }
        HashMap  subCount = new HashMap<>();
        int left = 0, right=1;
        //统计满足条件的字符数
        int count = 0;
        while(right<=s.length()){
            char newChar = s.charAt(right-1);
            if(tCount.containsKey(newChar)) {
                subCount.put(newChar, subCount.getOrDefault(newChar, 0) + 1);
                if(subCount.get(newChar)<=tCount.get(newChar))
                    count++;
                
            }
            while (count==t.length() && left

 

复杂度分析

        时间复杂度：O(|s|)。内外双重循环只是移动左右指针遍历了两遍s；而且由于引入了count，对子串是否符合条件的判断可以在常数时间内完成，所以整体时间复杂度为O(|s|+|t|)，近似为O(|s|)。

        空间复杂度：O(c)，这里c表示字符集的大小。用到了HashMap来存储s和t的字符频次，而每张哈希表中存储的键值对不会超过字符集的大小。

4. 找到字符串中所有字母异位词

力扣https://leetcode.cn/problems/find-all-anagrams-in-a-string/

4.1 问题描述

        给定两个字符串 s 和 p，找到 s 中所有 p 的 异位词 的子串，返回这些子串的起始索引。不考虑答案输出的顺序。

        异位词 指由相同字母重排列形成的字符串（包括相同的字符串）。

输入：s = "abab", p = "ab"

输出：  [0,1,2]

接受：

起始索引等于 0 的子串是 "ab", 它是 "ab" 的异位词。
起始索引等于 1 的子串是 "ba", 它是 "ab" 的异位词。
起始索引等于 2 的子串是 "ab", 它是 "ab" 的异位词。

4.2 解决方法

4.2.1 暴力法

        直接遍历s中每一个字符，把它当作子串的起始，判断长度为p.length()的子串是否是p的字母异位词。

        考虑到子串和p中都可能有重复字母，用一个额外的数据结构，来保存每个字母的出现频次。由于本题的字符串限定只包含小写字母，所以可以简单地用一个长度为26的int类型数组来表示，每个位置存放的分别是字母a~z的出现个数。

public class FindAnagrams1 {
    public List findAnagrams(String s, String p) {
        int[] counts = new int[26];
        //记录p中字符及其数量
        for (int i = 0; i < p.length(); i++) {
            counts[p.charAt(i) - 'a']++;
        }
        List res = new ArrayList<>();
        //遍历s
        for (int i = 0; i <= s.length() - p.length(); i++) {
            boolean isMath = true;
            int[] subCounts = new int[26];
            for (int j = i; j < i + p.length(); j++) {
                subCounts[s.charAt(j)-'a']++;
                //如果字串中的相同字符数大于p中的则将标志位记作false，并跳出当前循环
                if(subCounts[s.charAt(j)-'a']>counts[s.charAt(j)-'a']){
                    isMath = false;
                    break;
                }
            }
            if(isMath){
                res.add(i);
            }
        }
        return res;
    }

    public static void main(String[] args) {
        String s="abab", t = "ab";
        FindAnagrams1 findAnagrams = new FindAnagrams1();
        System.out.println(findAnagrams.findAnagrams(s, t));
    }
}

复杂度分析

        时间复杂度：O(|s| * |p|)，其中|s|表示s的长度，|p|表示p的长度。时间开销主要来自双层循环，循环的迭代次数分别是(s.length-p.length+1)和 p.length, 所以时间复杂度为O((|s|-|p|+1) * |p|), 去除低阶复杂度，最终的算法复杂度为 O(|s| * |p|)。

        空间复杂度：O(1), 需要两个大小为 26 的计数数组，分别保存p和当前子串的字母个数。尽管循环迭代过程中在不断申请新的空间，但是上一次申请的数组空间可以得到复用，所以实际上一共花费了2个数组的空间，因为数组大小是常数，所以空间复杂度为O(1)。

4.2.2 滑动窗口

        暴力法的缺点是显而易见的：时间复杂度较大，运行耗时较长。

        在暴力求解的时候，其实对于很多字母是做了多次统计的。子串可以看作字符串上开窗截取的结果，可以定义左右指针向右移动，实现滑动窗口的作用。在指针移动的过程中，字符只会被遍历一次，时间复杂度就可以大大降低

public class FindAnagrams2 {
    public List findAnagrams(String s, String p) {
        int[] counts = new int[26];
        //记录p中字符及其数量
        for (int i = 0; i < p.length(); i++) {
            counts[p.charAt(i) - 'a']++;
        }
        List res = new ArrayList<>();
        //定义左右指针
        int left = 0, right = 1;
        int[] subCounts = new int[26];
        while (right<=s.length()){
            char c = s.charAt(right-1);
            subCounts[c - 'a']++;
            while (subCounts[c-'a'] > counts[c-'a'] && left

 复杂度分析

        时间复杂度：O(|s|)。 窗口的左右指针最多都到达 s 串结尾，s 串每个字符最多被左右指针都经过一次，所以时间复杂度为O(|s|)。

        空间复杂度：O(1)。只需要两个大小为 26 的计数数组，大小均是确定的常量，所以空间复杂度为O(1)