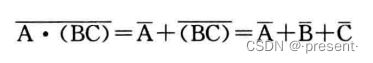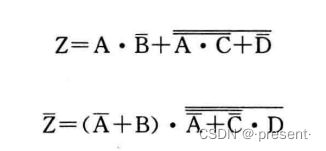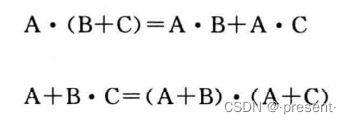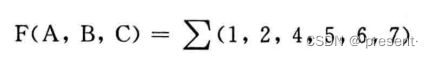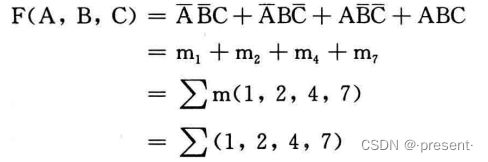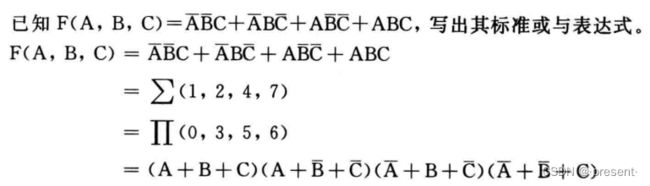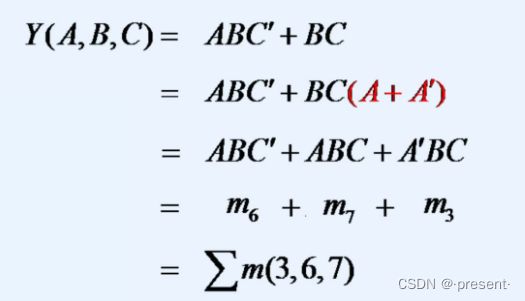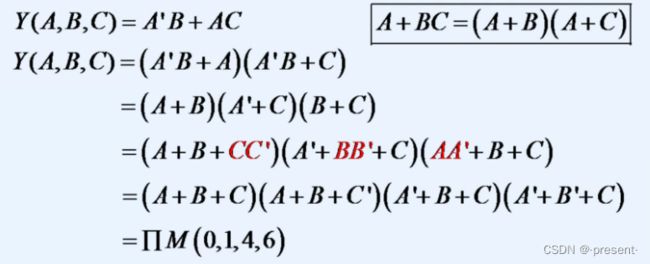逻辑函数常用的描述方法及相互间的转化
目录
一.三大规则
1.代入规则
2.反演规则
3.对偶规则
二.逻辑函数的描述方法
1.表达式
2.真值表
3.波形图
4.逻辑图
5.卡诺图
三.不同描述方法之间的转换
1.表达式——>真值表
2.真值表——>表达式
3.真值表——>卡诺图
4.卡诺图——>真值表
5.表达式——>卡诺图
6.卡诺图——>表达式
7.其它
一.三大规则
1.代入规则
描述：逻辑表达式两边同时出现的某个变量或者表达式，可以直接把所有的这个变量替换成另一个变量或者表达式，等式依旧成立.
PS:不一定需要这两个变量相同.
通俗地讲，就是我们方程中遇到过的等量代换，但这里我们并不要求两个变量相同，而是可以直接替换.
Lg.B不等于BC,但依旧可以替换.
2.反演规则
描述：对一个逻辑函数F，其中所有·变成+，+变成·，单变量全部求反，0变成1，1变成0
注意：变换过程要注意保持原函数中逻辑运算的优先顺序！！！不要变换后，本来先运算a,b，变成先运算a,c了.
比如下面的运算A,B先运算，那进行变换后，要记得加上括号，否则B就会和后面先运算了.
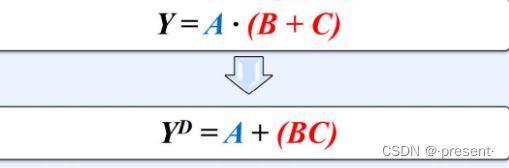
3.对偶规则
描述：对一个逻辑函数F，其中所有·变成+，+变成·，0变成1，1变成0
实际和反演规则非常相似，就是单变量不需要取反，当然记得要保持运算优先顺序！！！
PS：得到的对偶函数一般和原来是不相同的，但是两个函数相同，它们的对偶函数也是相同的.
先看上式，就是我们之前讲的分配律，分别对它们进行对偶运算，就可以轻松证明我们上次推理得到的式子.
二.逻辑函数的描述方法
1.表达式
由逻辑变量和逻辑运算符号组成，用来描述变量之间逻辑关系的式子就是逻辑表达式.
这其实我们已经很熟悉了，像之前举的F = A(B + C) = AB + AC,这就是常见的逻辑表达式
A,B,C之间通过加法，乘法等逻辑运算符结合在一起，描述它们之间和F的关系.
当然，在这里我们要先重点了解一些概念，为后面的不同描述方法转化做准备.
每一项都是与项，然后通过逻辑或结合在一起,这是一个与或表达式.
当每一项都包含所有的单变量，这时被称为标准与或表达式.
和与或表达式对应，或与表达式中每一项都是或项，然后通过逻辑与结合在一起,这是一个或与表达式.
同理，当每一项都包含所有的单变量，这时被称为标准或与表达式.
2.真值表
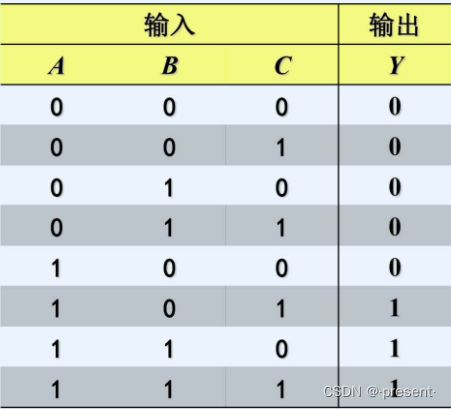
用来反映变量所有不同的取值组合，以及它们对应函数值的表格，称为真值表
如下图中，A有0，1两种逻辑取值，B有0，1两种逻辑取值，C有0，1两种逻辑取值
总共2*2*2=8种情况，按照自然顺序从小到大全部列在左边输入端，然后根据对应函数关系，给出不同函数值(输出)
3.波形图
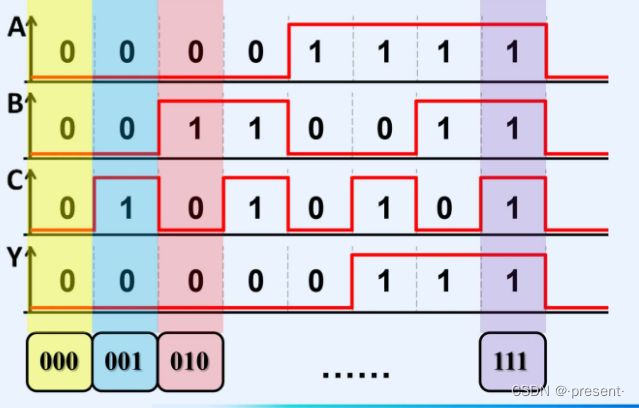
将输入变量所有可能取值与对应输出按时间顺序排列，画成时间波形.
实际上和真值表类似，只不过一个横着放取值，一个竖着放取值
如图，也是8列，对应不同的输出.
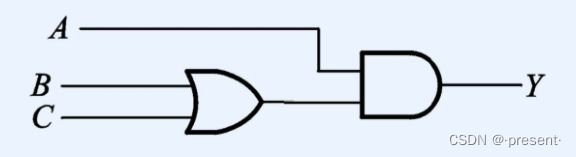
4.逻辑图
用逻辑图形符号表示逻辑运算关系，像下图就表示Y = A * (B + C)
5.卡诺图
将逻辑变量分成两组（怎么分取决我们，当然最好对半分，画出的表格更加美观，也更容易画）
分别在横竖两个方向用循环码形式排列出各组变量的一个取值组合，叫做卡诺图.
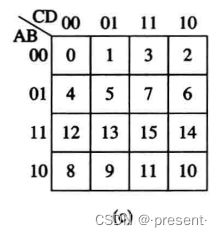
如下图，就是一个四变量的卡诺图，AB按循环码排列，CD也按循环码排列,然后括号里面没有放入对应的函数值，而是放入了对应变量取值组合的十进制数，也就是方格的编号.
这被称为变量卡诺图.
如果表格内放入的是对应函数值，则被称为函数卡诺图，如下图.
如何快速写出卡诺图的方格编号呢？
除了强行记忆（狗头），我们其实可以找些规律，循环码我们知道最低位是按0 1 1 0排列，而实际上应该是0 1 0 1，也就是每两列，每两行就要跳一下，发生转变.
三.不同描述方法之间的转换
本章主要讨论表达式，真值表，卡诺图三种描述方式的两两转化.
1.表达式——>真值表
首先把变量所有取值，按照自然二进制码顺序排列在左边
最简单一个方法就是把不同取值，代入表达式中，算出函数值，写到右边即可.
这当然没问题，但如果算错一个数，那就全盘皆输，是一个很考验耐心的活,能不能稍微简化一下呢？
答案是可以的，前面我们已经了解到与或表达式和或与表达式
如果先将逻辑函数化为与或表达式或者或与表达式
拿与或表达式来说，与或最后一步运算是逻辑或，假如有一项与项为1，那后面都不用看，最后输出肯定是1
那我们就可以一项项判断每一个与项什么时候取到1，函数值就是1，剩下的就为0
像上面的例子，先化简，变成与或表达式.
AC全为1，函数值为1；ABD全为0，函数值为1；ABD为1，C为0,函数值为1
剩下情况函数值全为0
这样是不是就能直接大大简化步骤呢？实际上还有另一种方法，直接看图，因为实际上按二进制排列，ABCD排列是有顺序的，可以不断对半切.
比方说下图的例子：
我先代入A为0，则下半部分可以切掉，再代入B为0，则函数可以化为F = 
，直接出答案，只有D为0的时候，函数值才为1.
然后代入B为1，化为F = C,也直接出答案.
2.真值表——>表达式
那如何根据真值表写出表达式呢？
我们受到上面的启发，可以根据真值表，先根据函数值为1的项写出它的与项，然后再全部用逻辑或，加起来不就行了？
但是这有一个前提，与项和函数值1是否一一对应呢？
假如函数值1，能够对应多个与项，那表达式就不是唯一的.
我们拿仅有A,B两个逻辑变量举例子,AB的与项总共有4种取法，对应二进制数取值也有4种取法
AB 
B A
00 01 10 11
我们把下面00 01 10 11分别代入AB中，只有11能使AB函数值为1
将11 分别代入 AB B A 中，只有AB为1
其余也可以类似得到，甚至推广更多变量，得到下面的结论：
标准与项都与变量的唯一一个取值组合相对应，只有这个组合能使标准与项取值为1，其余均是0.
PS：
1.所有不同标准与项相或必为1，因为必有1个标准与项对应函数值为1
2.任意两个不同的标准与项相与，必为0，不可能有一个取值对应的标准与项都为1
而且这个对应组合也很好写，因为对应函数值为1，一个变量一个变量来看，没有反则取1，有反则取0，比如ABC为111， 为00
标准与项对应变量取值组合大小，称为标准与项的编号
比如说ABC对应与项为1 1 1，则其编号为7，记为
所以标准与或表达式也可以用这种形式表示，写出其对应最小项的编号.
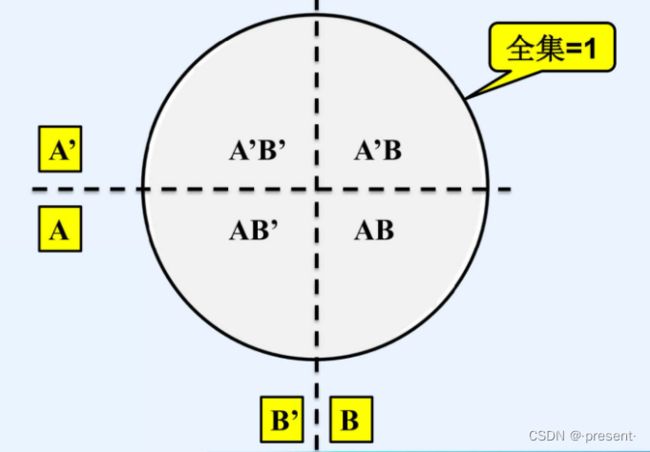
标准与项也被称为最小项
名字由来如下图显示那样，AB是全集中，最小的一个单位，只是其中的一块，所以被称为最小项.
有了上面的铺垫，我们便知道真值表如何转变为表达式
函数值为1的时候，可以根据变量取值也就是最小项的编号，轻松写出其对应的唯一最小项
再通过逻辑或运算，表示只要有一个最小项为1，函数值便为1，其余自然而然就为0
有最小项，那肯定就有最大项（或与表达式），去除掉最小项后，对应的就是最大项.
这里便用到我们前面提到的反演律,如下图所示
比如 C 和 A + B + 
一一对应，编号都是0 0 1 （函数值1取反为0，因此，最大项对应的唯
一函数值为0）
从这里我们也可以进一步得出：
由于我们想要输出的是函数值1，函数值为1的最小项，所对应的最大项的函数值刚刚好为0，
那剩余编号对应的最小项，所对应的最大项的函数值就必定是1.
因此.
我们可以将函数值为0的项（剩余编号对应的最小项），先写出最小项，再运用反演律得到最大
项，再利用逻辑与结合起来，就可以得到或与表达式.
反演律意味着取反，变号，函数值也会相应改变.
所以上述方法，还可以进一步化简为找函数值为0的项，，编号中取值为0，写原变量，编号中取值
为1，写反变量，然后组成与或项，写出标准或与表达式.
不过还有一种方法，就是根据编号来写.
同一函数，其标准与或表达式中最小项的编号和其标准或与表达式中最大项的编号是互补的
比如说下面的例子
与或表达式最小项的编号为1，2，4，7.
那相应的或与表达式最大项的编号为0，3，5，6.
对于最大项而言，编号中取值为0，写原变量，编号中取值为1，写反变量，然后组成与或项，写出标准或与表达式.
我们可以根据这个实现与或表达式和或与表达式之间的转化.
3.真值表——>卡诺图
卡诺图中也有编号，真值表也有编号，从真值表中函数值为1的变量组合，确定其大小编号，并在卡诺图中对应方格标上1即可.
当然假如你记住卡诺图的方格编号，真值表是按照顺序排列，那在对应卡诺图位置就可以迅速标出函数值为1的方格.
4.卡诺图——>真值表
和第三部分类似,只需要找出卡诺图中函数值为1的方格所对应的变量组合，并让真值表中让相应组合的函数值为1，即可得到函数真值表.
5.表达式——>卡诺图
和表达式化为真值表相类似，我们先将表达式化为与或表达式
再分别让每一与项为1，找出其对应卡诺图方格位置，标上1即可.
6.卡诺图——>表达式
和真值表化为表达式相类似，我们既可以找出卡诺图中函数值为1的，变量中取值为1，写原变量，变量中取值为0，写反变量，然后组成与项，写出标准与或表达式.
也可以找出卡诺图中函数值为0的，变量中取值为0，写原变量，变量中取值为1，写反变量，然后组成与或项，写出标准或与表达式.
而实际上，并不需要写出标准与或表达式，而仅仅写出与或表达式也是完全可以的.
7.其它
（1）或与表达式变标准或与表达式（最小项之和）
关键点：利用基本公式中A + = 1补全与项
从上面例子，可以看出，一个与项缺少一个变量，则生成两个最小项，依次类推，如果一个与项缺少n个变量，则生成2^n个最小项.
（2）与或表达式变标准与或表达式（最大项之积）
关键点：利用基本公式中A* = 0补全或项
从上面例子，可以看出，一个或项缺少一个变量，则生成两个最大项，一个或项缺少n个变量，则生成2^n个最大项.