经典网络解析（三）GoogleNet | Inception块，1*1卷积核，辅助分类器 整体结构代码

之前讲了

AlexNet的解析经典网络(一) AlexNet逐层解析 | 代码、可视化、参数查看！_Qodi的博客-CSDN博客

Vgg的解析

经典网络解析（二）Vgg | 块的设计思想，代码，小卷积核_Qodi的博客-CSDN博客

今天讲GoogleNet在2014年图像大赛中大放异彩

不同大小的卷积核有着各自的优势和缺点，所以有时使用不同大小的卷积核组合是更有利的。 本节将介绍一个稍微简化的GoogLeNet版本：

1. 串联结构VGG存在的问题

（1）后面的卷积层只能处理前层输出的特征图

​ 如果前层因为某些原因丢失了重要信息，后层无法找回

（2）参数太多，如果训练数据集有限，很容易产生过拟合；网络越大、参数越多，计算复杂度越大，难以应用

（3）网络越深，容易出现梯度弥散问题（梯度越往后穿越容易消失），难以优化模型。

2. GoogleNet结构解析

2.1 Inception块

提出Inception结构，可以保留输入信号中更多的信息

Inception块由四条并行路径组成。

（1）用1×1的卷积，只考虑压缩信息

（2）先用1×1的卷积（1×1卷积，以减少通道数，从而降低模型的复杂性，增加的1X1卷积后面也会跟着有非线性激励，这样同时也能够提升网络的表达能力），再用3×3的卷积，提取小感受野的信息，

（3）先用1×1的卷积（1×1卷积，以减少通道数，从而降低模型的复杂性，增加的1X1卷积后面也会跟着有非线性激励，这样同时也能够提升网络的表达能力。），再用5×5的卷积，提取大感受野的信息

（4）用3×3的最大化池化（进行非最大化抑制，相当于将原图的重要信息加强），再用1×1卷积（改变通道数）

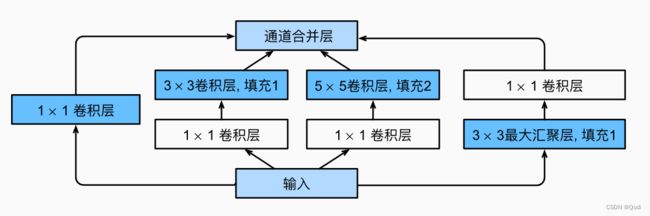
这四条路径都使用合适的填充来使输入与输出的高和宽一致

最后我们将每条线路的输出在通道维度上连结，并构成Inception块的输出。在Inception块中，通常调整的超参数是每层输出通道数。

最后把特征图的通道数连接在一起

比如（1）通道数64（2）通道数128（3）通道数32 ，（4）通道数32 那么则把通道数连接起来后就是256

通过Incention块，实现层数更深，参数更少，计算效率也更高

真实中堆叠了九层Inception

2.2 最后采用平均池化操作

用平均池化代替了原来的向量展开全连接层

比如最后有1024个特征图，每个特征图求一个平均值，那么经过平均之后就只有1024个值

1. 降低尺寸：平均池化操作通过计算池化窗口中所有像素值的平均值来减小特征图的尺寸。这有助于降低计算负担，减少网络中的参数数量，提高模型的计算效率。
2. 平移不变性：与最大池化类似，采用平均池化，丢掉了语义结构的空间位置信息，有助于提升卷积层提取到特征的平移不变性，即使目标在特征图中稍微移动了一点，平均池化仍然会产生相似的输出，从而有助于提高模型的鲁棒性。
3. 减少过拟合：通过减小特征图的尺寸，平均池化可以降低模型的容量，有助于减少过拟合的风险，从而提高模型的泛化能力。

2.3 辅助分类器

（1）位置：GoogleNet在网络的中间层添加了多个辅助分类器，通常分布在不同的Inception模块之间。这些分类器将中间层的特征图作为输入，并生成分类预测。

**（2）多尺度特征：**由于这些辅助分类器位于不同深度的层次中，它们能够捕获不同层次和尺度的特征信息。这有助于提高网络对不同大小目标的识别能力。

**（3）损失函数：**每个辅助分类器都有自己的损失函数，通常使用交叉熵损失（cross-entropy loss）来衡量其分类预测与真实标签之间的差异。这些辅助损失函数与主要分类器的损失函数一起用于计算模型的总损失。

**（4）梯度传播：**辅助分类器的存在有助于梯度从网络底部向上传播。在反向传播时，梯度可以从多个位置进入网络，避免了梯度在深层网络中逐渐减小，从而缓解了梯度消失问题。这提高了网络的训练稳定性，使得更深的网络能够更容易地收敛。

**（5）正则化效应：**辅助分类器可以看作一种正则化机制，因为它们要求不同层次的特征都具有一定的分类能力。这有助于减少过拟合风险，并提高网络的泛化能力。

需要注意的是，辅助分类器在训练期间使用，而在推理（inference）时通常被丢弃。它们的主要目的是在训练期间帮助网络学习更好的特征表示和提高训练速度。这个想法启发了后续深度学习模型的设计，例如ResNet等，它们也采用了类似的思想来改善梯度传播和训练稳定性。

3.代码实现

参照《动手学深度学习》，省略了一些为稳定训练而添加的特殊特性，书中说现在有了更好的训练方法，这些特性不是必要的。

3.1 实现Inception块

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l


class Inception(nn.Module):
    # c1--c4是每条路径的输出通道数
    def __init__(self, in_channels, c1, c2, c3, c4, **kwargs):
        super(Inception, self).__init__(**kwargs)
        # 线路1，单1x1卷积层
        self.p1_1 = nn.Conv2d(in_channels, c1, kernel_size=1)
        # 线路2，1x1卷积层后接3x3卷积层
        self.p2_1 = nn.Conv2d(in_channels, c2[0], kernel_size=1)
        self.p2_2 = nn.Conv2d(c2[0], c2[1], kernel_size=3, padding=1)
        # 线路3，1x1卷积层后接5x5卷积层
        self.p3_1 = nn.Conv2d(in_channels, c3[0], kernel_size=1)
        self.p3_2 = nn.Conv2d(c3[0], c3[1], kernel_size=5, padding=2)
        # 线路4，3x3最大汇聚层后接1x1卷积层
        self.p4_1 = nn.MaxPool2d(kernel_size=3, stride=1, padding=1)
        self.p4_2 = nn.Conv2d(in_channels, c4, kernel_size=1)

    def forward(self, x):
        p1 = F.relu(self.p1_1(x))
        p2 = F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3 = F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4 = F.relu(self.p4_2(self.p4_1(x)))
        # 在通道维度上连结输出
        return torch.cat((p1, p2, p3, p4), dim=1)

3.2 各个块依次实现

b1

第一个模块的第一个卷积层使用64个通道、7×7卷积层（尺寸减半）然后经过池化层

第二个卷积层依然使用64个通道、3×3卷积层，然后经过池化层

第三个卷积层通道数升为192、3×3卷积层，然后经过池化层

b1=nn.Sequential(
    nn.Conv2d(1,64,kernel_size=7,stride=2,padding=3),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1),
    nn.Conv2d(64,64,kernel_size=1),
    nn.ReLU(),
    nn.Conv2d(64,192,kernel_size=3,padding=1),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)

b2

b2模块串联两个完整的Inception块。

第一个Inception块中，第二个和第三个路径首先将输入通道的数量分别减少到96/192=1/2和16/192=1/12，然后连接第二个卷积层。最终Inception的输出通道数为64+128+32+32=256，

第二个Inception块中，第二条和第三条路径首先将输入通道的数量分别减少到128/256=1/2和32/256=1/8。然后连接第二个卷积层。最终Inception的输出通道数为128+192+96+64=480，

b2=nn.Sequential(
    Inception(192,64,(96,128),(16,32),32),
    Inception(256,128,(128,192),(32,96),64),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)

b3

b3它串联了5个Inception块，其输出通道数分别是192+208+48+64=512、160+224+64+64=512、128+256+64+64=512、112+288+64+64=528和256+320+128+128=832。

思路和前面一样

b3=nn.Sequential(
    Inception(480,192,(96,208),(16,48),64),
    Inception(512,160,(112,224),(24,64),64),
    Inception(512,128,(128,256),(24,64),64),
    Inception(512,112,(144,288),(32,64),64),
    Inception(528,256,(160,320),(32,128),128),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)

b4

包含输出通道数为256+320+128+128=832和384+384+128+128=1024的两个Inception块。 其中每条路径通道数的分配思路和前面一致，只是在具体数值上有所不同。

需要注意的是，第五模块的后面紧跟输出层，使用全局平均汇聚层，将每个通道的高和宽变成1。 最后我们将输出变成二维数组，再接上一个输出个数为标签类别数的全连接层。

b4=nn.Sequential(
    Inception(832,256,(160,320),(32,128),128),
    Inception(832,384,(192,384),(48,128),128),
    nn.AdaptiveAvgPool2d((1,1)),
    nn.Flatten()
)

最后把他们拼起来 接一个全连接层做分类

net=nn.Sequential(

  b1,b2,b3,b4,

  nn.Linear(1024,10)

)

完整代码

我们模拟一个[1,3,227,227]图像的输入，看每一层的输出形状

import torch
from torch import nn
from torch.nn import functional as F
from d2l import torch as d2l

class Inception(nn.Module):
    def __init__(self, in_channels,c1,c2,c3,c4, **kwargs) -> None:
        super().__init__(**kwargs)
        self.p1_1=nn.Conv2d(in_channels,c1,kernel_size=1)
        self.p2_1=nn.Conv2d(in_channels,c2[0],kernel_size=1)
        self.p2_2=nn.Conv2d(c2[0],c2[1],kernel_size=3,padding=1)
        self.p3_1=nn.Conv2d(in_channels,c3[0],kernel_size=1)
        self.p3_2=nn.Conv2d(c3[0],c3[1],kernel_size=5,padding=2)
        self.p4_1=nn.MaxPool2d(kernel_size=3,stride=1,padding=1)
        self.p4_2=nn.Conv2d(in_channels,c4,kernel_size=1)
    def forward(self,x):
        p1=F.relu(self.p1_1(x))
        p2=F.relu(self.p2_2(F.relu(self.p2_1(x))))
        p3=F.relu(self.p3_2(F.relu(self.p3_1(x))))
        p4=F.relu(self.p4_2(self.p4_1(x)))
        return torch.cat((p1,p2,p3,p4),dim=1)



b1=nn.Sequential(
    nn.Conv2d(3,64,kernel_size=7,stride=2,padding=3),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1),
    nn.Conv2d(64,64,kernel_size=1),
    nn.ReLU(),
    nn.Conv2d(64,192,kernel_size=3,padding=1),
    nn.ReLU(),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)

x=torch.randn(1,3,227,227)
for layer in b1:
    x=layer(x)
    print(layer.__class__.__name__,"output shape:",x.shape)
b2=nn.Sequential(
    Inception(192,64,(96,128),(16,32),32),
    Inception(256,128,(128,192),(32,96),64),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)
for layer in b2:
    x=layer(x)
    print(layer.__class__.__name__,"output shape:",x.shape)

b3=nn.Sequential(
    Inception(480,192,(96,208),(16,48),64),
    Inception(512,160,(112,224),(24,64),64),
    Inception(512,128,(128,256),(24,64),64),
    Inception(512,112,(144,288),(32,64),64),
    Inception(528,256,(160,320),(32,128),128),
    nn.MaxPool2d(kernel_size=3,stride=2,padding=1)
)
for layer in b3:
    x=layer(x)
    print(layer.__class__.__name__,"output shape:",x.shape)

b4=nn.Sequential(
    Inception(832,256,(160,320),(32,128),128),
    Inception(832,384,(192,384),(48,128),128),
    nn.AdaptiveAvgPool2d((1,1)),
    nn.Flatten(),
    nn.Linear(1024,10)
)
for layer in b4:
    x=layer(x)
    print(layer.__class__.__name__,"output shape:",x.shape)

net=nn.Sequential(
    b1,b2,b3,b4
)

输出

Conv2d output shape: torch.Size([1, 64, 114, 114])
ReLU output shape: torch.Size([1, 64, 114, 114])
MaxPool2d output shape: torch.Size([1, 64, 57, 57])
Conv2d output shape: torch.Size([1, 64, 57, 57])
ReLU output shape: torch.Size([1, 64, 57, 57])
Conv2d output shape: torch.Size([1, 192, 57, 57])
ReLU output shape: torch.Size([1, 192, 57, 57])
MaxPool2d output shape: torch.Size([1, 192, 29, 29])
Inception output shape: torch.Size([1, 256, 29, 29])
Inception output shape: torch.Size([1, 480, 29, 29])
MaxPool2d output shape: torch.Size([1, 480, 15, 15])
Inception output shape: torch.Size([1, 512, 15, 15])
Inception output shape: torch.Size([1, 512, 15, 15])
Inception output shape: torch.Size([1, 512, 15, 15])
Inception output shape: torch.Size([1, 528, 15, 15])
Inception output shape: torch.Size([1, 832, 15, 15])
MaxPool2d output shape: torch.Size([1, 832, 8, 8])
Inception output shape: torch.Size([1, 832, 8, 8])
Inception output shape: torch.Size([1, 1024, 8, 8])
AdaptiveAvgPool2d output shape: torch.Size([1, 1024, 1, 1])
Flatten output shape: torch.Size([1, 1024])
Linear output shape: torch.Size([1, 10])

4 贡献总结

GoogleNet只有500万参数，比AlexNet少12倍

1. Inception模块引入：GoogleNet引入了Inception模块，这是一种高效的卷积神经网络模块，通过使用多尺寸的卷积核并行处理输入数据，大大提高了网络的感受野（receptive field），并且在不增加太多参数的情况下增加了网络的深度和宽度。这使得网络能够更好地捕捉不同尺度和层次的特征。
2. 网络深度和性能平衡：GoogleNet在当时的深度学习研究中展示了在适当的条件下，增加网络的深度并不一定会导致过拟合。相反，它展示了如何通过适当的网络设计，使更深的网络具有更好的性能。
3. 辅助分类器：GoogleNet引入了辅助分类器，这些分类器位于网络的中间层，有助于解决梯度消失问题，并提高网络的训练稳定性。这个想法启发了后续深度学习模型的设计，例如ResNet。
4. 计算效率：GoogleNet通过使用1x1卷积核和平均池化等技术，降低了网络的计算复杂度，使得更深更宽的网络仍然能够高效地训练和推理。这对于实际应用中的计算资源管理至关重要。